Resource Allocation for Two⁃Tier RIS⁃Assisted Heterogeneous NOMA Networks

XU Yongjun ,YANG Zhaohui ,HUANG Chongwen ,YUEN Chau ,GUI Guan

(1.School of Communication and Information Engineering,Chongqing University of Posts and Telecommunications,Chongqing 400065,China；2.Department of Electronic and Electrical Engineering,University Col⁃lege London,London WC1E 6BT,UK；3.College of Information Science and Electronic Engineering,Zhejiang University,Hangzhou 310027,China；4.Engineering Product Development Pillar,Singapore University of Technology and Design,Singapore 487372,Singapore；5.College of Telecommunications and Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)

Abstract: Reconfigurable intelligent surface (RIS) as a promising technology has been proposed to change weak communication environ‑ments.However,most of the current resource allocation (RA)schemes have focused on RIS-assisted homogeneous networks,and there is still no open works about RA schemes of RIS-assisted heterogeneous networks (HetNets).In this paper,we design an RA scheme for a RISassisted HetNet with non-orthogonal multiple access to improve spectrum efficiency and transmission rates.In particular,we jointly optimize the transmit power of the small-cell base station and the phase-shift matrix of the RIS to maximize the sum rates of all small-cell users,subject to the unit modulus constraint,the minimum signal-to-interference-plus-noise ratio constraint,and the cross-tier interference constraint for protecting communication quality of microcell users.An efficient suboptimal RA scheme is proposed based on the alternating iteration ap‑proach,and successive convex approximation and logarithmic transformation approach.Simulation results verify the effectiveness of the pro‑posed scheme in terms of data rates.

Keywords:heterogeneous networks;non-orthogonal multiple access;reconfigurable intelligent surface;resource allocation

1 Introduction

Recently,reconfigurable intelligent surface (RIS) as a promising technology has been proposed to improve energy efficiency (EE) and transmission quality by re‑configuring the wireless propagation environ‑ment[1-4].Particularly,a RIS has a large number of low-cost passive reflecting elements which can reflect the incident sig‑nals from the transmitters by changing the phase shift (PS) of the RIS in a passive way.Since the RIS is connected with a base station (BS) by a RIS controller,the reflected signal can be smartly configured to strengthen the desired signal and sup‑press the undesired signal for meeting the transmission re‑quirements of communication systems.

1.1 Related Work

According to the above advantages of RIS,resource allocation(RA) problems for RIS-assisted networks have been concerned by many scholars.For example,the authors in Ref]5] proposed a low-complexity iteration algorithm to maximize the spectrum ef‑ficiency (SE) by jointly optimizing the beamformer at the BS and the PS of the RIS in a point-to-point RIS-assisted multiple-input single-output (MISO) communication system.But only one user is considered.To overcome the effect of imperfect channel state information (CSI),a weighted sum-rate maximization problem for the multiuser scenario was investigated by jointly designing the active beamforming of the access point (AP) and the passive beamforming of the RIS under perfect/imperfect CSI in Ref]6],where stochastic successive convex approximation (SCA) was used to obtain the solution.But the minimum signal-tointerference plus-noise ratio (SINR) constraint is not considered,and it fails to meet the required quality of service (QoS) of each user.Considering the same communication network as in Ref]6],the transmit power and the PS of the RIS were jointly de‑signed in Ref]7] to maximize the total EE by using an alternat‑ing iteration approach and the sequential fractional program‑ming.Moreover,in Ref]8],the total transmit power of the AP was minimized by jointly optimizing the transmit beamforming of the AP and the reflect beamforming of the RIS,subject to the SINR of each user.In Ref]9],a particle swarm optimization method was used to minimize the total transmit power.However,the above works[5-9]consider the RIS-assisted MISO system.For a RIS-assisted multiple-input multiple-output (MIMO) net‑work[10],a weighted sum-rate maximization RA problem was stud‑ied by jointly optimizing the precoding matrices of the BS and the PS of the RIS,subject to the maximum power constraint of each BS and the unit modulus constraint of the RIS,where a RIS at the cellular edge was developed to assist the downlink trans‑mission for cell-edge users.The classical block coordinate de‑scent (BCD) algorithm,the Majorization-Minimization algorithm and the complex circle manifold method were used to deal with the non-convex problem.The authors in Ref]11] proposed a lo‑cal search method to maximize the sum rate in a RIS-assisted Terahertz communication system.For a RIS-assisted simultane‑ous wireless information and power transfer (SWIPT) system[12],the authors studied the RA problem of the weighted sum power maximization of multiple energy-harvesting receivers.In Ref]13],a theoretical outage performance comparison between nonorthogonal multiple access (NOMA) and orthogonal multiple ac‑cess(OMA)in the RIS-assisted downlink communication was ana‑lyzed.Moreover,the power minimization problem and performance analysis for RIS-aided NOMA systems have been studied in Ref]14] and Refs]15-17],respectively.The performance compari‑sons between the new RIS system and the traditional decode-andforward relaying system were studied in terms of total transmit power minimization and the EE maximization[18].Moreover,other related works on the RIS-assisted scenario have been studied from space shift keying[19],channel estimation[20],etc.

1.2 Motivation and Contributions

However,the above works[6-20]have not considered the RA problem in heterogeneous networks(HetNets).HetNet as an im‑portant technique in 6G communications[21]can obviously im‑prove communication coverage and network capacity by deploy‑ing small cells into the macrocell[22-23].However,the QoS of in‑door users is heavily degraded by interior walls and strong fad‑ing channels.Thus,it is a natural idea to combine RIS and Het‑Net to exemplify received signals and expand communication coverage.Besides,the introduction of NOMA can improve SE and allow more accessing users.Different from the RA problem in traditional NOMA systems,our work needs to simultaneously optimize transmit power and phase shifts to further improve SE and signal received quality at the receivers.

In this paper,we study the RA problem for a downlink RISassisted heterogeneous NOMA network,where a small-cell BS(SBS) transmits wireless signals to the targeted users whose signals are enhanced with the help of the RIS.The RA prob‑lem for such a system is still in its infancy.The contributions of this paper are summarized as follows.

• A two-tier RIS-assisted heterogeneous NOMA network is formulated,where a single-antenna SBS transmits wireless sig‑nals to multiple single-antenna small-cell users (SCUs)with the assistance of the RIS.For the single-user scenario,the rate maximization RA problem is formulated by jointly optimizing the transmit power of the SBS and the PS of the RIS under the SINR constraint of the macro-cell user (MCU) and the maxi‑mum transmit power constraint.A Dinkelbach-based iteration scheme is proposed to globally obtain the optimal solutions.

• For the multiuser scenario,the total rate maximization problem is formulated under the cross-tier interference con‑straint,the maximum transmit power,and the unit modulus constraint of the RIS.To deal with the non-convex problem,we propose an efficient RA scheme based on a semi-definite programming (SDP) approach and SCA to obtain the subopti‑mal solution by an alternating iteration manner.

• Simulation results show that the proposed scheme has good convergence and transmission rates.

The rest of this paper is organized as follows.In Section 2,the system model and the single-user RA problem are intro‑duced.Section 3 proposes a multi-user RA scheme for the multiuser scenario.Section 4 verifies the effectiveness of the proposed scheme.Section 5 concludes this paper.

2 System Model and Single-User RA Problem

2.1 System Model

A downlink two-tier RIS-assisted HetNet with NOMA is given in Fig.1,where a RIS withMpassive reflecting units is employed to enhance the transmission quality between the SBS andKNOMA SCUs.A macro base station (MBS) servesNMCUs.The SCUs can share the spectrum owned by MCUs via an underlying spectrum way.Since the RIS is developed in interior walls,where the reflected signals from the RIS caused by MCUs can be ignored.A separate wireless control link serves for information exchange between the RIS controller and the SBS,and other required information for implementing the transmit power[10].Motivated by the works[5-7],perfect CSI and continuous phase-shift coefficients are assumed here.For the single-user scenario,definingh=[h1,...,hM]H∈CM×1,g=[g1,...,gM]H∈CM×1,f=[f1,...,fM]H∈CM×1andφ=[φ1,...,φM]Has the channel gain from the SBS to the RIS,the channel gain from the RIS to the SCU,the channel gain from the RIS to the MCU,and the reflecting coefficient (RC) of the RIS,where eachφm=βmejθmcomprises an amplitude coeffi‑cientβm∈[0,1].Similar to Refs]5-9],a continuous PS co‑efficient is assumed,e.g.,θm∈[0,2π] and|φm|=1.gSMandgSSare the channel gains from the SBS to the MCU and the SBS to the SCU.DefineΦ=diag(φ) ∈CM×Mas the RC ma‑trix of the RIS.Since we aim to obtain the maximum designed signal,the amplitude coefficient is set asβm=1 for simplic‑ity[24].Ignoring signals reflected by the RIS for two and more times[25],the received SINRs at the SCU and the MCU are

whereσ2represents the noise power at the receiver.

2.2 Single-User RA Scheme

Motivated by the existing works in Refs]5-10],the power allocation and PS ratio under the single-user scenario are jointly optimized by using an alternating iteration approach.However,the solution is just a suboptimal solution.In order to deal with this challenge,we try to get the optimal power alloca‑tion and PS solution under a single-user scenario.

Under this special case,we want to improve the transmis‑sion rate of the SCU by adjusting the transmit power and PS coefficients in a globally optimal solution way,while the QoS of the MCU is guaranteed.Therefore,the rate-maximization problem of the SCU is formulated as whereC1denotes the QoS required by the MCU under the con‑sideration of the interference power from the RIS and the SBS,γminrepresents the SINR threshold of the MCU.C2accounts for the fact that each RIS reflecting element can only provide a phase shift,without amplifying the incoming signal.C3denotes the transmit power range of the SBS,andpmaxis the maximum transmit power at the SBS.Since we want to find the optimalp*andφ*,the maximum transmit power of the MBS is ignored.

Based onC1,the upper bound ofpis

Based on the monotonicity ofpin the objective function in Problem(3),the optimal transmit power becomes

To obtain the globally optimal solution,we substitutep*into Problem (3),the PS coefficient optimization problem of Prob‑lem(3)can be reformulated as

Based on Dinkelbach’s method[26],we have

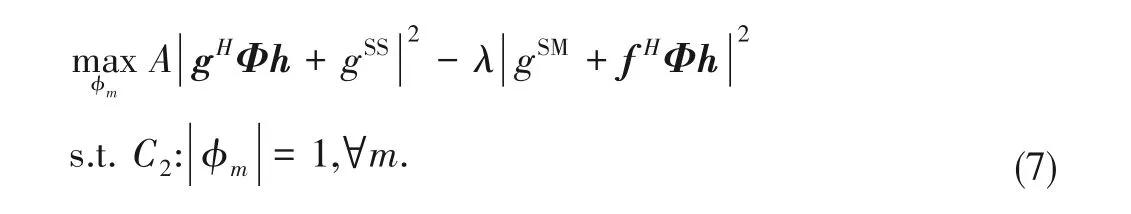
whereλis an auxiliary variable.Obviously,the objective func‑tion of Problem (7) is a strictly continuous and decreasing function withλ.

Proof:See Appendix A.

Sinceφ=[φ1,...,φM]H,=diag(g)hand=diag(f)h,Problem(7)becomes

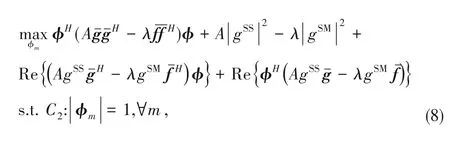
where Re{⋅}denotes the real part of a complex number.

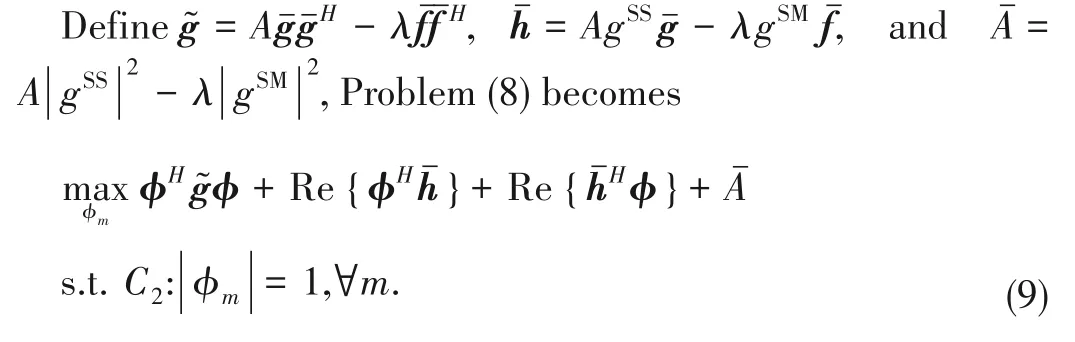
Problem (9) is a non-convex quadratically constrained qua‑dratic program (QCQP) problem[27],which can be converted into a homogeneous QCQP problem.By introducing an auxil‑iary variablet(t≥0),Problem(9)becomes

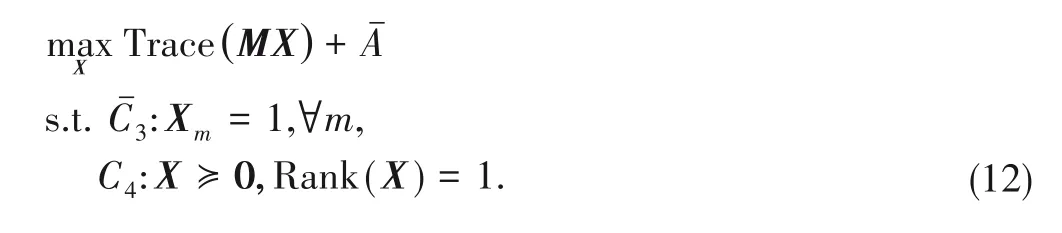
By relaxing the rank-one constraint,Problem (12) is a con‑vex SDP problem[26],which can be efficiently solved by using the convex optimization tool,e.g.,SeDuMi[28].Generally,the solutionXof Problem (12) does not satisfy its rank con‑straint[28],namely,Rank(X)≠1,while the objective function of Problem (12) only serves an upper bound of it.To obtain a rank-one solution,the Gaussian randomization scheme can be used[29].As a result,an iteration-based RA scheme is summa‑rized in Algorithm 1.The convergence of Algorithm 1 is ana‑lyzed in Appendix B.

Algorithm 1.A Dinkelbach-based RA Scheme

3 Multi-User RA Scheme

Since the single-user scenario is a specific case for practical systems,it is only helpful to analyze system performance,which is too ideal for practical two-tier RIS-aided communication sys‑tems.In order to improve system capacity and support massive connectivity,in this section,we extend the special case of Prob‑lem (3) to the multi-user NOMA scenario.Assuming that there areKNOMA SCUs andNMCUs,the sets are denoted as K={1,2,...,K},∀k∈K and N={1,2,...,N},∀n∈N.The signal of the SBS is,wherepkandxkdenote the allo‑cated power and the signal from the SBS to thek-th SCU,re‑spectively.Therefore,the signal received at thek-th SCU is

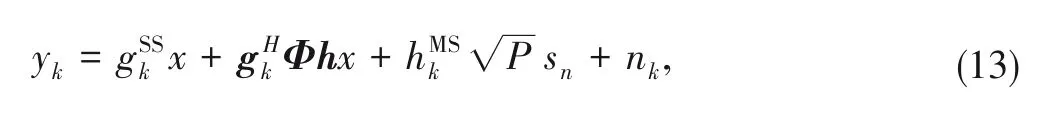
where the first item in the denominator denotes the interfer‑ence power from other SCUs,and the second item denotes the cross-tier interference from the MBS to the SCUk.Since the MBS is often far from SCUs,the interference power of the mac‑rocell network can be omitted[31].

Thus,the total sum rate for all SCUs is

Since we only consider the transmit power optimization problem for SCUs due to the lower priority in spectrum usage,the joint optimization problem of the transmit power of SBS and the transmit power of MBS are beyond the scope of this paper.Thus,we assume that the MBS allocates the same trans‑mit powerPto each MCU.Thus,the received signal at thenth MCU can be formulated as

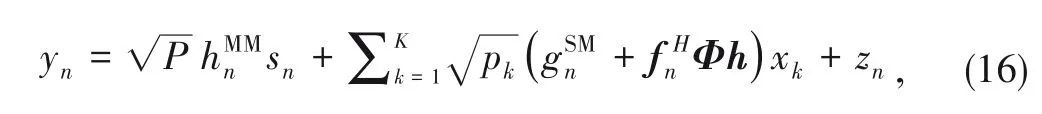
wherezn～CN (0,)denotes the received AWGN at then-th MCU receiver with zero mean and variance.

As a result,the SINR received at then-th MCU is

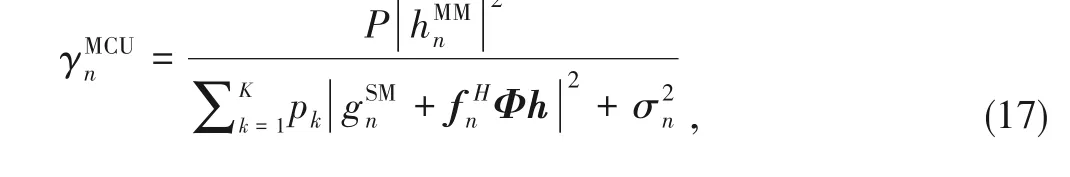
Thus,the sum-rate maximization RA problem of the consid‑ered RIS-assisted heterogeneous NOMA network becomes

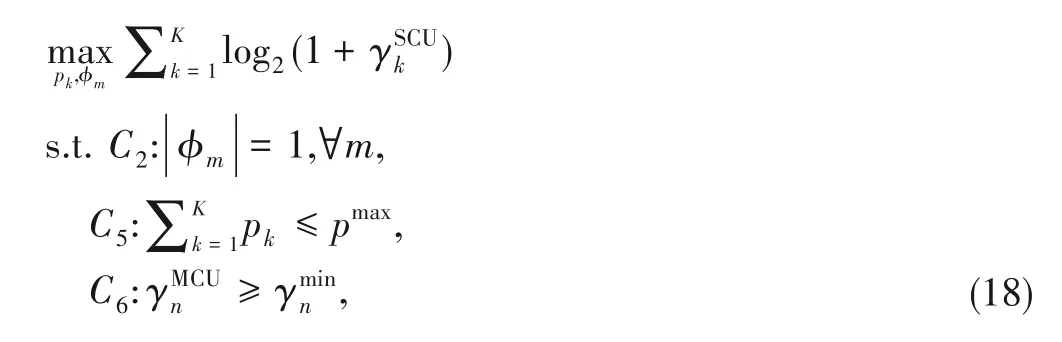
3.1 Optimizing pk with Given φm

Based onC6,we have

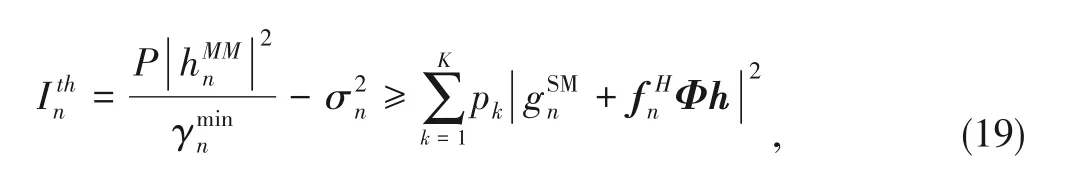
wheredenotes the interference power limit of MCUn.

As a result,the power allocation subproblem of Problem(18)becomes

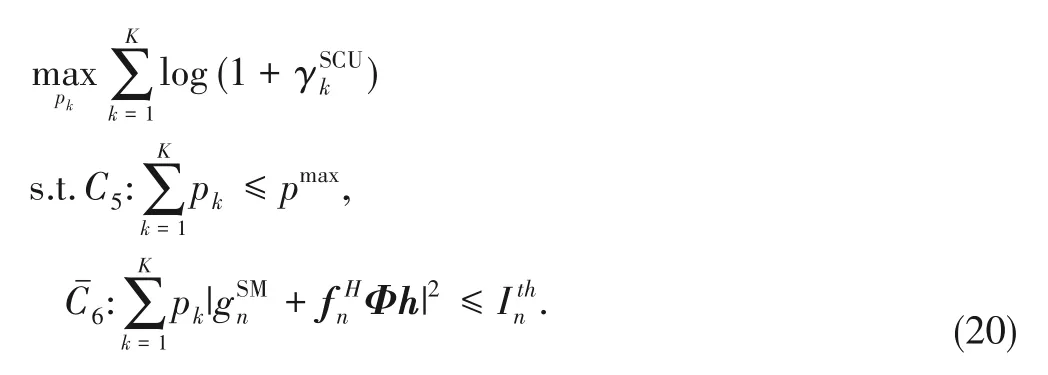
It is noted thatC5andare linear constraints,but the ob‑jective function is nonconvex.

Based on the successive convex approximation for low com‑plexity (SCALE) algorithm in Ref]32],for anyz＞0,we have the following bound:

As a result,we have the following sum rate

which is a lower bound of the sum rate achieved by SCUs.Note that the relaxation is still a non-convex form due to the difference of convex(d.c.)structure.

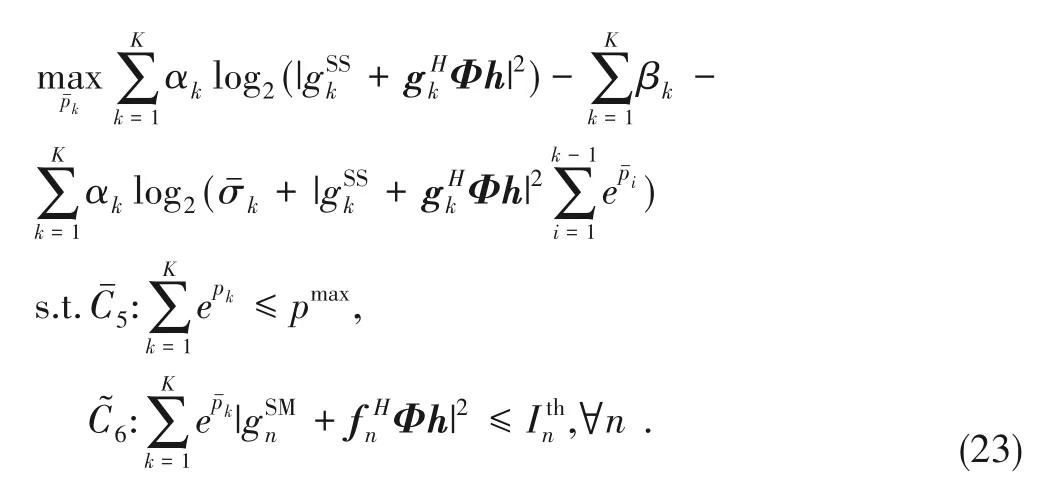
Problem (23) is a standard concave maximization problem since the log-sum-exp is convex[33].Considering the convexity of Problem (23),the closed-form solution of power allocation can be obtained by using the Lagrange dual theory.Thus,the Lagrange function of Problem(23)can be written as

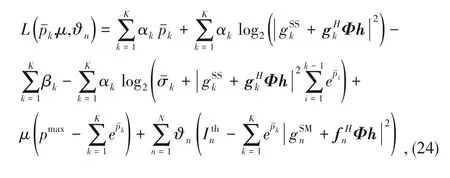
whereμandϑnare the non-negative Lagrange multipliers.

Based on Karush-Kuhn-Tucker (KKT)conditions,the trans‑mit power is calculated by

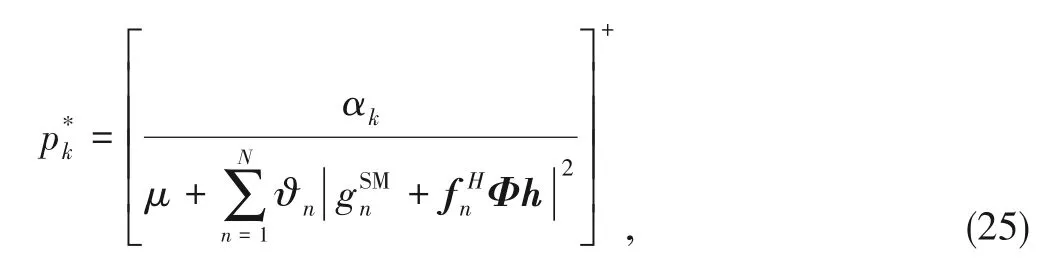
where[x]+=max{0,x}.

Based on the sub-gradient updating method,Lagrange mul‑tipliers can be calculated by

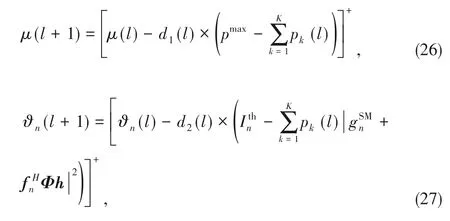
wherelis the iteration number.d1(l) ≥0 andd2(l) ≥0 de‑note the sufficiently small step sizes.When they satisfy the fol‑lowing relationship,we have

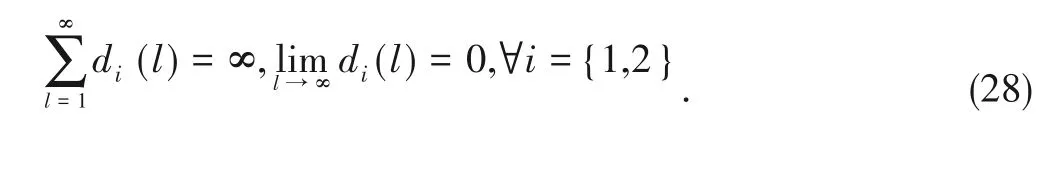
The sub-gradient updating iteration algorithm can fast con‑verge.The dual variablesμ(l+1) andϑn(l) will converge to the optimal valuesμ∗and,∀n,∀nasl→∞.Note that the duality gap for Problem (23)is zero and the solution is unique.As a result,the primal variable(μ(l),ϑn(l)) can reach its targeted value,∀k.

3.2 Optimizing φm with Given

Now,we perform the optimization overφmwith the fixed.Then,Problem(23)is equivalent to

Problem(29)is the sum of multiple-ratio fractional program‑ming problems,and the non-convexity introduced by the frac‑tional objective function and the non-convex unit-modulus constraint.We adopt a relaxation method to solve Problem(29)efficiently.

whereyk≥0 is an auxiliary variable.

Defining=diag(gk)h,C7can be rewritten as

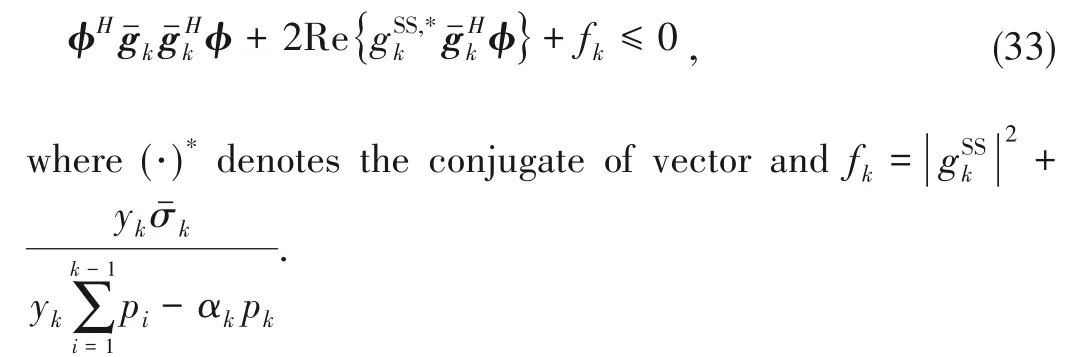
In addition,C2can be rewritten as

whereU∈M×Mis a symmetric matrix with elements of ze‑ros,except forum,m=1.

Thus,we have

As a result,the Lagrange function of Problem (35) can be written as

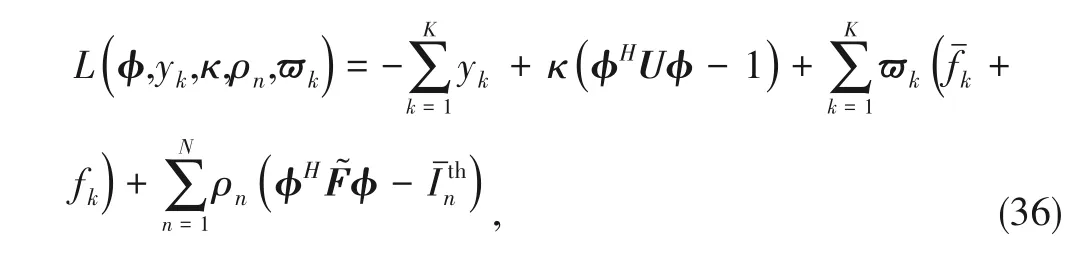
whereκ,ϖk,andρnare the non-negative Lagrange multipliers.

Based on KKT conditions,the solution ofcan be ob‑tained as

where the Lagrange multipliers are updated by

whered3(l),d4(l) andd5(l) are the step sizes.Based on the same approach in Problem (28),the sub-gradient-based itera‑tive method can guarantee the convergence of the proposed al‑gorithm.

Algorithm 2.An Iterative RA Scheme

In order to solve the PS coefficient,based on a Schur complement,the dual problem of Problem(35)becomes

3.3 Computational Complexity

For the multi-user system,the complexity of the algorithm mainly depends on the number of users and the optimization approach.Regarding to Algorithm 2,it involves the inner and outer iterations.The inner layer is used to obtain variablespandΦrespectively,while the outer layer is taken for alternat‑ing iterations.We denote the maximum alternating iteration number asLouter,and the iteration numbers of obtainingpandΦasLIandLJrespectively.There exists a polynomial-time complexity(K(N+1))to solvepby using sub-gradient updat‑ing methods.Therefore,its computational complexity is(K(N+1)LI).Similarly,the computational complexity of the SDP problem to solveφmis,whereL=M3+M6+M3(M+1)2(M3+M+1) +M9andwis the convergence precision of the SDP problem.Based on the above discussion,the total complexity of Algorithm 2 is.

4 Simulation Results

In this section,simulation results are given to demonstrate the effectiveness of the proposed RA scheme by comparing it with the rate-maximization based RA scheme without RIS[33]which is defined as“the traditional RA scheme without RIS”.A spectrum-sharing small cell is randomly distributed in the coverage area of the macrocell.SCUs are uniformly distributed in the coverage area of their associated SBS.The coverage radii of the macrocell and small cell are 500 m and 20 m,respec‑tively.The distance-dependent path loss model for the largescale fading is given by,wheredmis the distance be‑tween the SBS to the reflecting unitmof RIS,rkis the distance between the RIS and the SCUk,andαdenotes the path loss ex‑ponent.The distance between the SBS and the RIS is 10 m.The distance between RIS and the SCU is 5 m.The small-scale fading is considered as Rayleigh fading channel[13].The stop‑ping criterion for convergence isε=10-6.The noise power isσ2=-100 dBm,andα=3.The simulation setup is shown in Fig.2.The detailed parameter settings are shown in Table 1.

4.1 Single-User Case

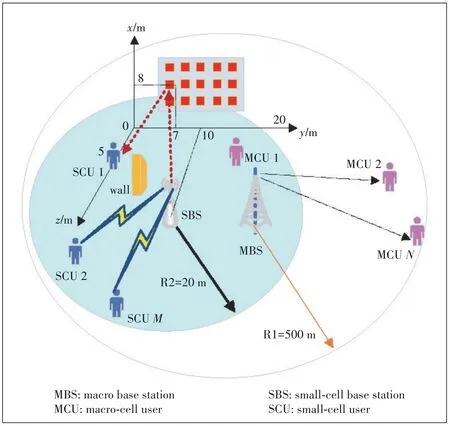
▲Figure 2.Simulation setup

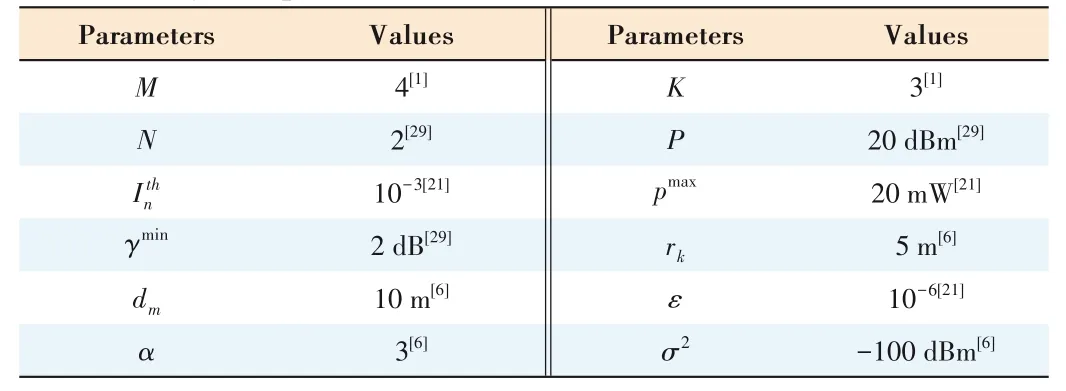
▼Table 1.System parameters

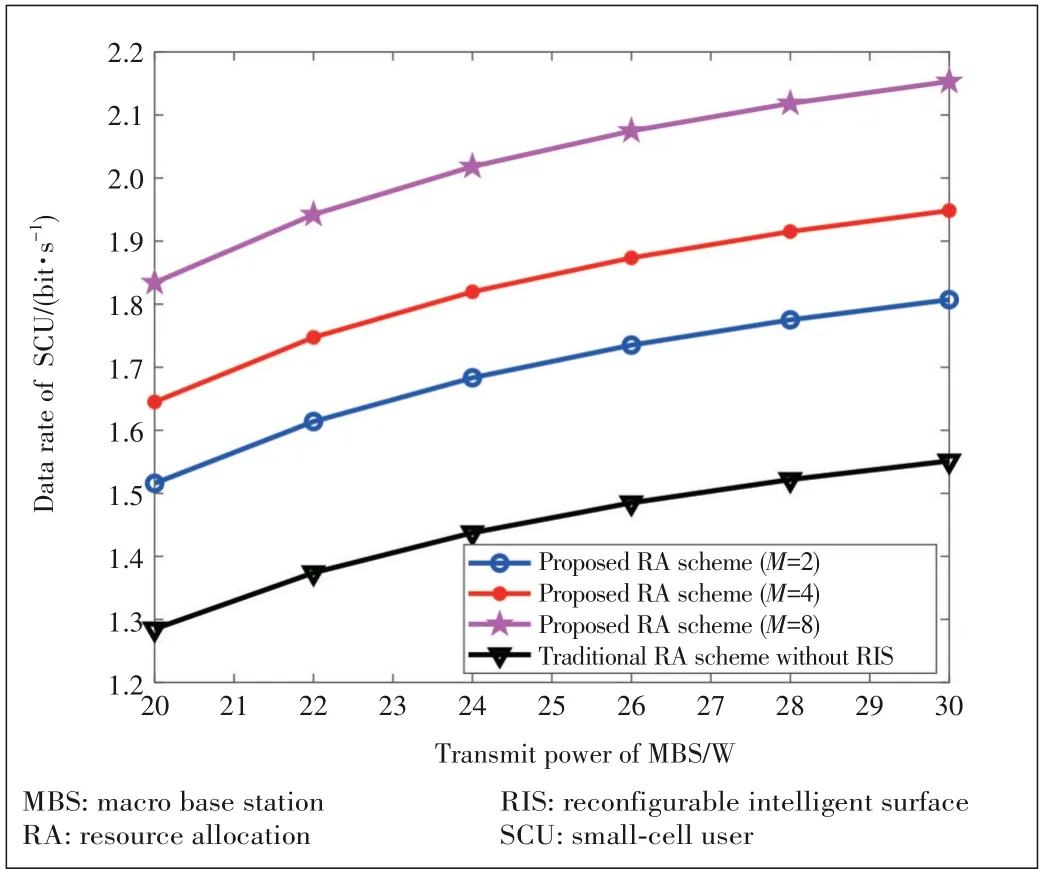
▲Figure 3.Data rate of SCU versus transmit power of the MBS P

Fig.3 depicts the data rate of the SCU versus the transmit power at the MBS.The target SINR of MCU isγmin=2 dB.From this figure,the data rate of the SCU improves quickly as the increasing transmit powerP.The reason is that the large transmit power of the MBS increases the available transmit power from the SBS to the SCU according to the constraintC1.Besides,this figure also shows that the data rate under the pro‑posed RA scheme is larger than that of the RA scheme with‑out RIS,which indicates that the RIS can improve the rate per‑formance in a passive reflecting way.Moreover,the data rate increases heavily with the increasing number of reflecting ele‑ments at the RIS,which indicates that a massive number of pas‑sive reflecting elements brings better performance improvement.

Fig.4 shows the data rate of the SCU versus the minimum SINR requirement of the MCU (e.g.,γmin).The transmit power of the MBS is assumed to beP=20 dBm.With the increasingγmin,the data rate of the SCU decreases a lot.The reason is that,under the fixed transmit power at the MBS,the allowed transmit power from the SBS to the SCU becomes smaller to avoid less interference power to the MCU.It is noted that as for the achieved transmission performance,i.e.,the achieved data rate,the proposed RA scheme is better than that of the RA scheme without RIS.

Fig.5 gives the allocated power to the SCU versus the num‑ber of reflecting elementsMunder different transmit power of the MBSP.It is observed that the required transmit power of the proposed RA scheme is around 40% lower than that of the RA scheme without RIS under different transmit powerP.This dem‑onstrates that the energy consumption can be reduced a lot when the RIS is adopted.Moreover,the received transmit power at the SCU decreases with the increasing number of reflecting ele‑mentsM.Because larger reflecting elements provide more multipath interference to the MCU.The available transmit power of the SBS decreases for guaranteeing the QoS of the MCU(namely,cross-tier interference constraint).When the transmit power at the MBS is increased,the available transmit power at the SBS is increased accordingly,since large transmit power at the MBS allows more transmit power to improve the communica‑tion quality of SCU via constraint(4).

▲Figure 4.Data rate of SCU versus SINR threshold of MCU γmin

4.2 Multi-User Case

The numbers of SCUs and MCUs areK=3 andN=2,respec‑tively.The reflecting elements areM=4.Assume that each MCU receiver has the same interference power limit.The maximum transmit power of the SBS ispmax=20 mW,and the interference power limit is=10-3mW[33].

Fig.6 shows the convergence performance of the proposed RA scheme.It is observed that the allocated power to each SCU can quickly reach the equilibrium points within eight it‑erations,which demonstrates that the proposed RA scheme has a good convergence.

▲Figure 5.Allocated power from SBS to small-cell user (SCU) versus the number of reflecting elements M

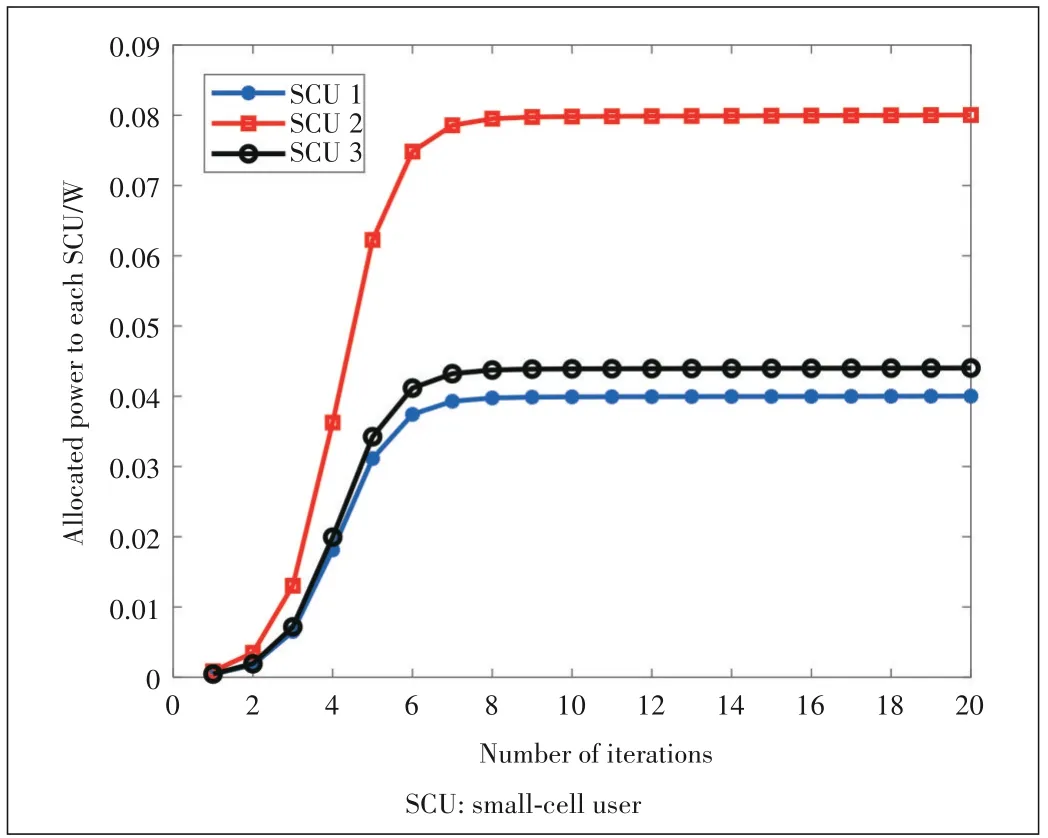
▲Figure 6.Convergence of proposed resource allocation(RA)scheme

Fig.7 shows the sum rate of all SCUs versus the number of reflecting elements with different SCUs.It is observed that the total rate achieved by SCUs under the proposed RA scheme increases with the increasing number of reflecting elements.Since the RIS can provide more reflecting signals to strengthen the desired signals to SCUs.However,the to‑tal rate of SCUs under the traditional RA scheme always keeps stable with the increasing number of reflecting ele‑mentsMsince no RIS is deployed in this scheme.Besides,the total rate of SCUs with a largeKis better than that with a smallK.The gap of the total rate of SCUs under a smallmis larger than that under a largeM.Because the interfer‑ence power among different SCUs is small due to less trans‑mission path,the total rate is decided by the number of us‑ers.Thus,there is a big performance gap in the region with small reflecting elements.However,due to the effect of the cross-tier interference constraint,the overall performance of SCUs is limited.It is impossible to unrestrictedly im‑prove the performance with the increasing number of re‑flecting elementsM.

Fig.8 shows the total rate of SCUs versus the different inter‑ference power limit of MCU.The total rate of SCUs in‑creases with the increasing.The biggermeans that the MCU can tolerate more harmful interference power from SCUs and RIS.Correspondingly,the SBS allocates more transmit power to each SCU for pursuing a higher data rate.Moreover,the proposed RA scheme with a largerMachieves better per‑formance than the other two cases.The reason is that the RIS can effectively enhance system performance by providing mul‑tiple flexible transmission paths.

5 Conclusions

In this paper,we have maximized the total rate of SCUs by jointly optimizing the transmit power at the SBS and PS coeffi‑cients at the RIS in RIS-assisted heterogeneous NOMA net‑works.Specifically,we firstly propose an optimal RA scheme to maximize the transmission rate of the SCU in a single-user scenario,subject to the SINR constraint of MCU,the maxi‑mum transmit power constraint of SBS,and the PS coefficient constraint.Then,we design a suboptimal RA scheme to maxi‑mize the total rate of SCUs for the multi-user scenario,subject to the sum transmit power constraint of the SBS,the cross-tier interference constraint of each MCU,and the unit modulus constraint of the RIS.The alternating iteration approach and the SCA approach are used to solve the originally non-convex optimization problem.Simulation results show that the pro‑posed RA scheme has a good converge and transmission rate compared with the traditional RA scheme without RIS.In our future work,we will study the joint optimization of beamform‑ing and PS coefficients under the discrete PS constraint and imperfect CSI in a multi-antenna heterogeneous NOMA net‑work with RIS.

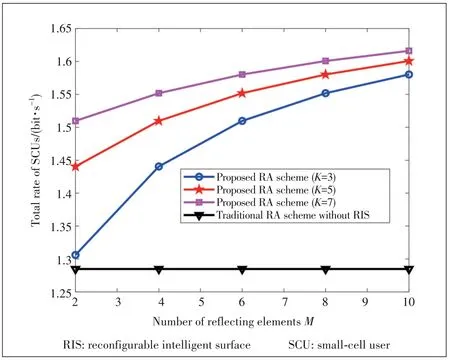
▲Figure 7.Total rate of SCUs versus the number of reflecting elements M

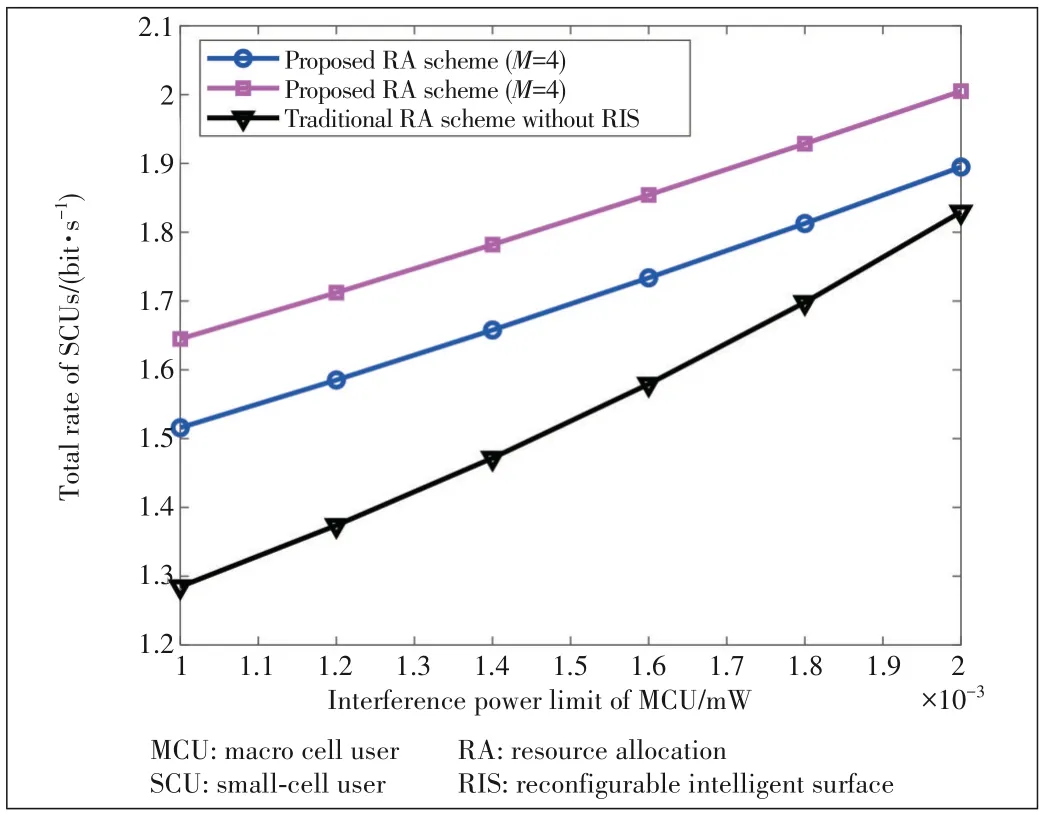
▲Figure 8.Total rate of SCUs versus the interference power limit of the MCU

Appendix A:Proof of Theorem 1

Based on Problem (7),an equivalent objective function is given by

Assume there are two optimal auxiliary variablesλ1andλ2(λ1＞λ2) for the optimal phase shift policiesΦ1andΦ2,respectively,then

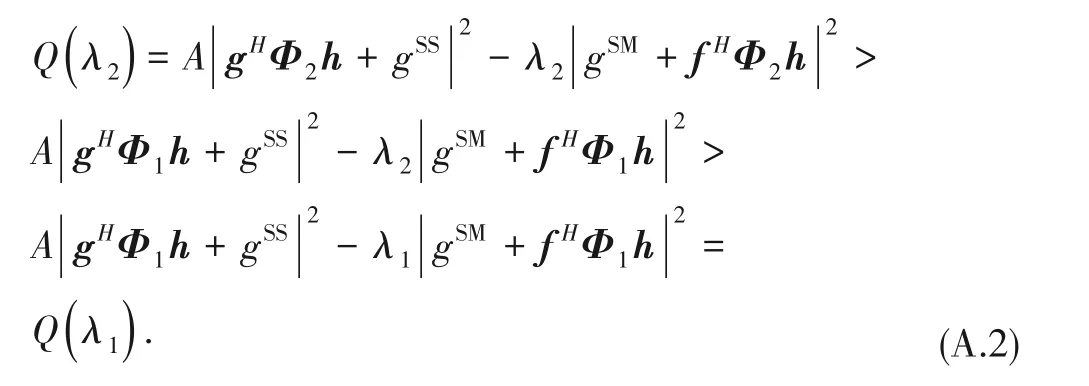
Therefore,Q(λ) is a strictly decreasing function with the variableλ.DefineΦ'as any solution for Problem(7)and

As a result,we haveQ(⋅) ≥0.The proof is complete.

Appendix B:Proof of Convergence

According to the algorithm procedure of Algorithm 1,the convergence is determined by the Dinkelbach-based ap‑proach.To show the convergence of Dinkelbach's method,we define(λ(l),φm(l))as the optimal solution in thel-th iter‑ation,λ(l) ≠λ*andλ(l+1) ≠λ*as the EE at thel-th and(l+1)-th iteration,respectively.We have the following prop‑osition.

Proposition:If (λ',φ'm) is an arbitrary feasible solution of Problem(7),we have

Based on the Proposition,we haveF(λl,Φ(l)) ＞0 andF(λl+1,Φ(l+1)) ＞0 because ofλ(l) ≠λ*andλ(l+1) ≠λ*.As a result,F(λl,Φ(l)) ＞0 can be rewritten as

Sinceλ(l+1) ＞λ(l),whileF(λ,Φ) is a strictly decreas‑ing function inλaccording to Theorem 1,we can show that with the increase of iterations,F(λ(l),Φ(l))can gradually ap‑proach to zero,namely.Accordingly,we haveλ(l+1)=λ(l),l→∞.Thus,the Dinkelbach-based approach can guarantee the convergence of the algorithm.The proof is complete.