Markovian Cascaded Channel Estimation for RIS Aided Massive MIMO Using 1⁃Bit ADCs and Oversampling

1 Introduction

Massive multiple-input multiple-output (MIMO) has been identified as a key technology for future com‑munication systems

.In fact,large spatial degrees of freedoms (DoFs) can increase spectral efficiency without requiring extra spectral resources.Recently,recon‑figurable intelligent surfaces (RISs) have been proposed as a cost-effective technology for tuning the wireless propagation channel among transceivers

.A RIS consists of a large num‑ber of meta-atoms that can be controlled by the software to modify their phase shifts,so that incident electromagnetic waves can be mostly reflected to the desired receiver,which makes the wireless transmission more energy-efficient.The combination of RIS and massive MIMO is treated as one of the promising technologies for the sixth-generation wireless com‑munication systems

.

The channel estimation method for RIS aided massive MIMO systems is a serious challenge,since there exist two cascaded channels,namely,the channel between the users and the RIS and the channel between the RIS and the base station (BS),to be estimated.The acquisition of channel state information (CSI) has been recently studied in Refs]4-7].TAHA et al.

considered a RIS architecture which is a mix‑ture of active and passive elements.This method facilities the channel estimation but increases the hardware cost and energy consumption.In Ref]5],a non-iterative two-stage channel estimation framework for passive RIS aided millimeter-wave MIMO systems was proposed,where every stage is formulated as a multi-dimensional direction-ofarrival estimation problem.Similarly,the authors in Ref]6]have proposed a two-stage channel estimation algorithm,namely,sparse matrix factorization and matrix completion,to exploit the rank-deficient structure of the channel.In Ref]7],the cascade channel estimation is converted into a sparse signal recovery problem by utilizing the properties of Katri-Rao and Kronecker products.

The receiver design in massive MIMO systems,however,becomes more challenging since the power consumption in‑creases rapidly as the number of antennas grows.Among all the components in the radio frequency (RF) chain,a large portion of the total power consumption lies in the analog-todigital converters (ADCs),whose power consumption grows exponentially with the number of quantization bits

.The deployment of current high-resolution (8-12 bits) ADCs is a critical bottleneck for the practical use of large-scale MIMO.To alleviate this issue,the use of low-resolution ADCs (1-4 bits) can largely reduce the power consumption and is more suitable for the deployment of large-scale MIMO systems.

In this paper,we consider the extreme case of 1-bit resolu‑tion,where the in-phase and quadrature components of the re‑ceived samples are separately quantized to 1 bit.This solution is particularly attractive to massive MIMO systems,since each of the RF chains only contains simple limiting amplifiers(LAs) without the automatic gain control (AGC).This hard‑ware change can largely reduce both the power consumption and the hardware cost at the BS.Prior works on 1-bit massive MIMO have analyzed the sum rate

,channel estimation

,and signal detection

.Moreover,oversampling is applied to further compensate for the performance loss caused by the coarse quantization

.Furthermore,the distortion caused by 1-bit quantization and the sample correlation caused by oversampling make the cascaded channel estimation problem even more challenging.

In this paper,we develop an approximate message passing(AMP)based algorithm to solve the considered cascaded chan‑nel estimation problem,where the received signal is sampled at a rate beyond Nyquist sampling and quantized to 1-bit.Bussgang decomposition is applied to deal with the coarse quantization and a Markov chain is developed to characterize the correlation of adjacent oversampled samples.The corre‑sponding factor graph is presented and the AMP algorithm is derived.Unlike prior works on AMP-based cascaded channel estimation

,this work considers the statistical characteris‑tic of 1-bit quantization and uses the oversampling technique to increase the estimation accuracy.Simulations show that our proposed algorithm outperforms the method in Refs]7-8]and can even approach the 2-bit Nyquist-sampled systems in terms of the normalized mean square error (NMSE) while the former consumes less power at the receiver.

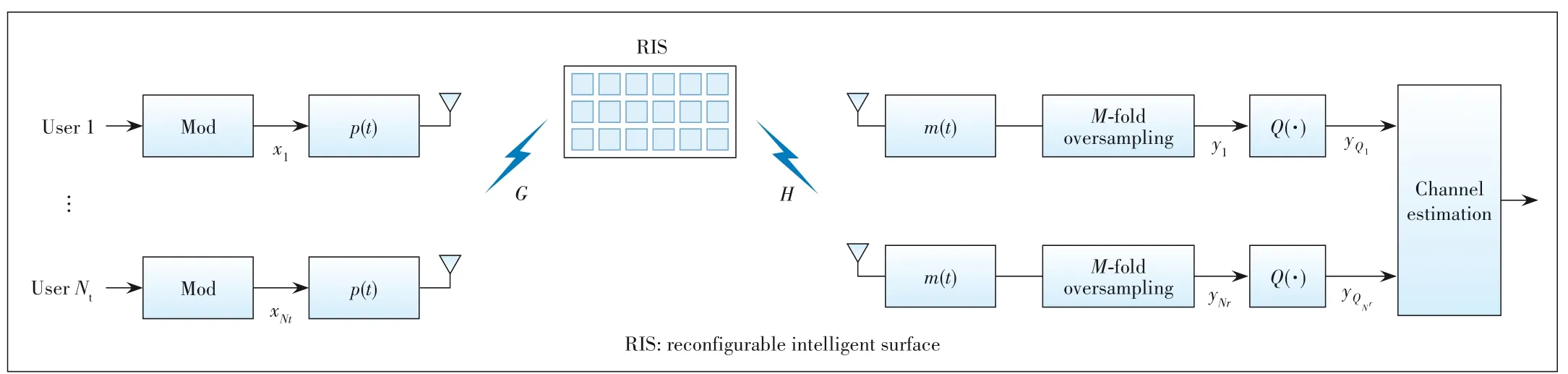
2 System Model and Problem Statement

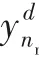
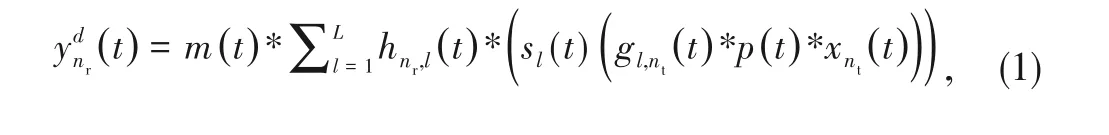
where

x

(

)is the transmitted signal from the

-th user;

s

(

)represents the

-th reflecting element at the RIS;

g

(

) and

h

(

) are the channel impulse responses from the user

to the

-th reflecting element and from the

-th reflecting element to the

-th receive antenna,respectively;* denotes the opera‑tion of convolution.

But what compensation did he get for having been imprisoned a whole year, and shut out from allcommunication with his fellow creatures? They told him he wasfortunate in being proved innocent, and that he might go

Flat fading channels are considered in this work,i.e.,

g

(

)and

h

(

)can be written as

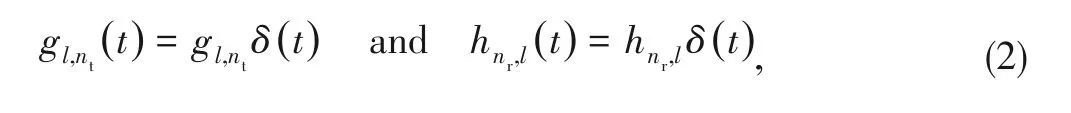
where

g

and

h

are the corresponding channel gains and

(

)is the Dirac delta function.Consider a transmission block with length

:

You can answer, and you can speak, and I will marry you; but do you know that every word which we are saying and have said has been taken down and will be in the paper to-morrow? By each window do you see there are standing three reporters and an old editor, and this old editor is the worst, for he doesn t understand anything! but she only said this to tease Blockhead-Hans

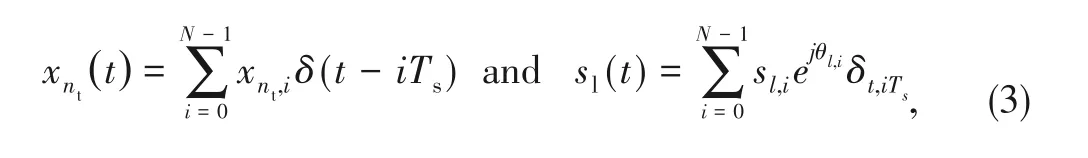
where

is the symbol duration;

x

is the transmitted symbol at the time instant

;

s

∈{0,1} is the on/off state

and

θ

∈(0,2π]is the phase shift of the

-th reflecting element of RIS at the time instant

;

δ

is the Kronecker delta function,where

δ

=1 for

=

and

δ

=0 otherwise.Eq.(1) can be simplified as:

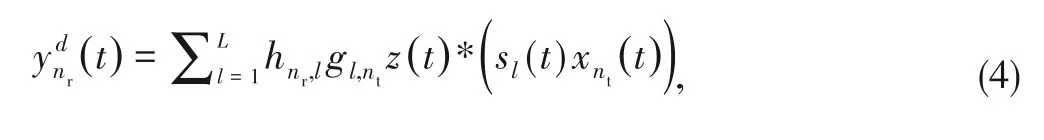
where

(

)=

(

)*

(

).In oversampled systems,Eq.(4) can be discretized as:

where

∈R

is the Toeplitz matrix with the form as

In Eq.(6),

=[0,...,0,1]

∈R

is the zero-inserting vec‑tor and

I

denotes the

×

identity matrix.Furthermore,⊗represents the Kronecker product and diag(

) is a diagonal matrix with the diagonal specified by

.In particular,

=1 refers to the case of Nyquist sampling rate.

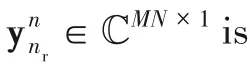
Combining Eqs.(6) and (8),the received oversampled samples at the

-th receive antenna

∈C

are

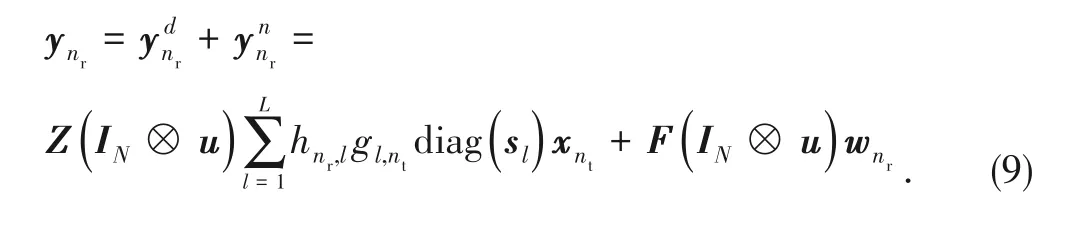
Defining

″ ≜

(

I

⊗

),

″ ≜

(

I

⊗

),and stacking the

-th received oversampled samples on top of the previous receive antenna,Eq.(9)is extended to

With Eqs.(16) and (19),the posterior probability

(

,

|

y

)is calculated as

The problem to be solved is estimating the channel param‑eters in

and

.The minimum mean square error(MMSE)es‑timators of the channel matrices are given by

One evening, when the artificial bird was singing its best, and the emperor lay in bed listening to it, something inside the bird sounded “whizz.” Then a spring cracked. “Whir-r-r-r” went all the wheels, running round, and then the music stopped. The emperor immediately sprang out of bed, and called for his physician; but what could he do? Then they sent for a watchmaker; and, after a great deal of talking and examination, the bird was put into something like order; but he said that it must be used very carefully, as the barrels were worn, and it would be impossible to put in new ones without injuring the music. Now there was great sorrow, as the bird could only be allowed to play once a year; and even that was dangerous for the works inside it. Then the music-master made a little speech, full of hard words, and declared that the bird was as good as ever; and, of course no one contradicted him.

A few days later, I returned to the school to visit. I noticed Ronny on a bench near the playground, the book open in his lap. I could see his lips move as he read to himself

Based on the Bayes’rule,the closed-form solutions of Eq.(12)are given by

{

|

y

}and

{

|

y

}.For avoiding the high computational complexity of calculating

(

|

y

) and

(

|

y

)in the marginalization of

(

,

|

y

),a practical messagepassing based algorithm is presented in the next section.

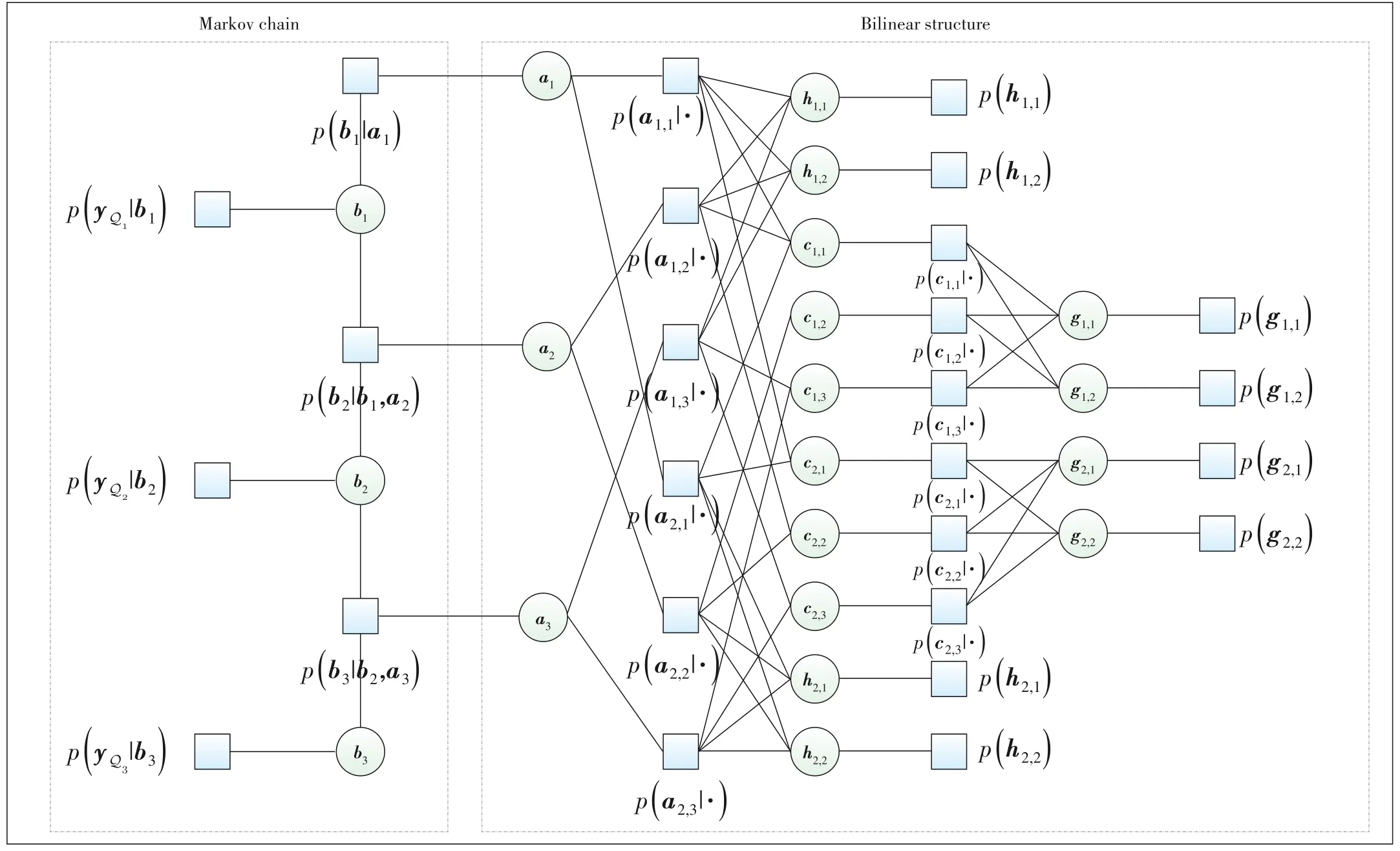
3 Markovian Cascaded Channel Estimation

3.1 Markov Chain for Oversampling

Due to the banded structure of the matrix

in Eq.(7),we develop a Markov chain,where every two adjacent columns in

are combined together for defining one state

b

as

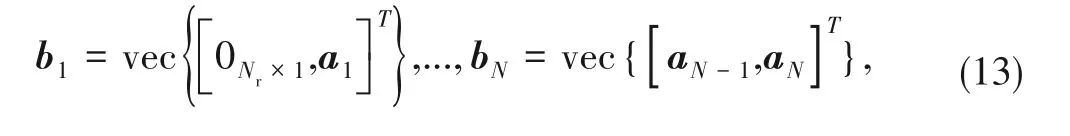
and each state is with the mean and covariance:

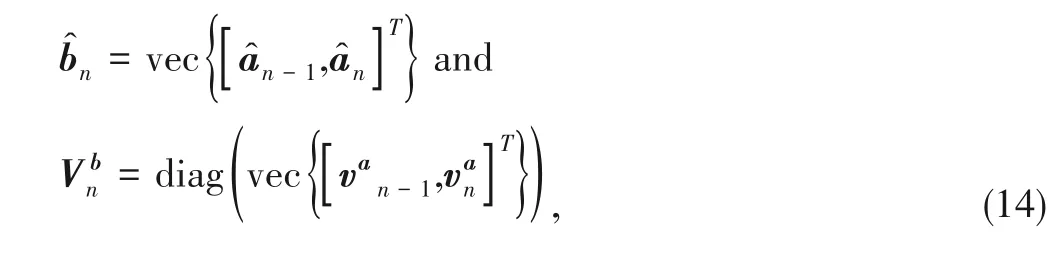
with

a

∈C

being the

-th column of

.The transition function from the current state to the next is

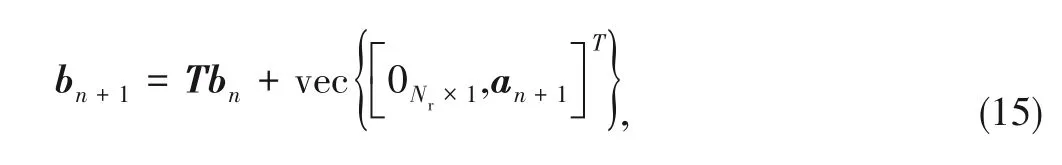
where

=

I

⊗[0,1;0,0]and the conditional probability is given by

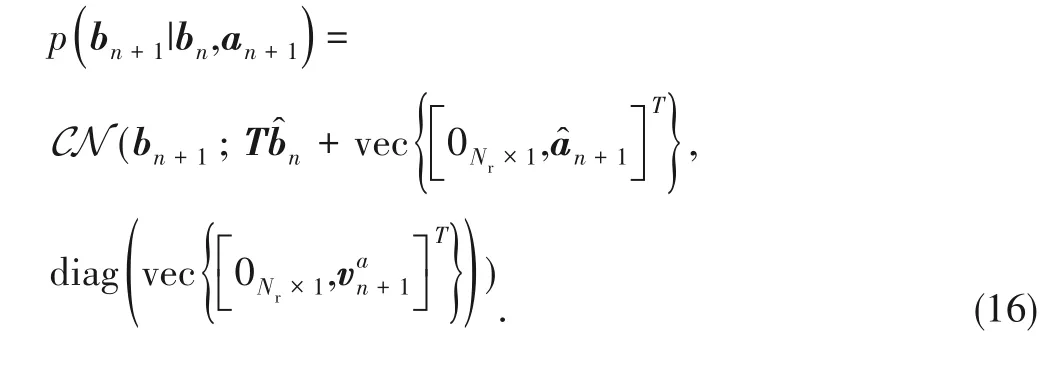
During the message updates,the covariance of

at the

-th iteration is

V

(

),and Eq.(23)can be rewritten as

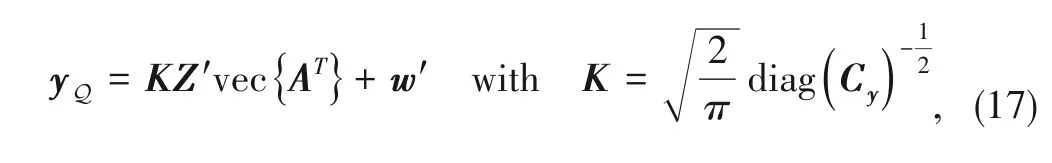
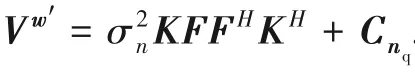
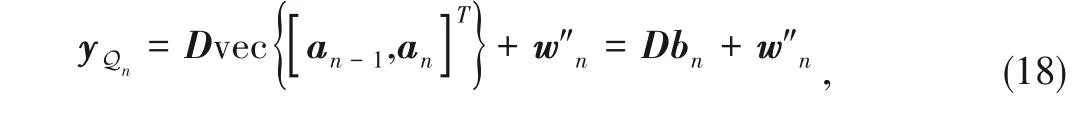
where

≜(

I

⊗[0

I

])

KZ

'

;

K

∈C

,

'

∈C

and

″

∈C

represent the correspond‑ing submatrices of

,

' and

',respectively.The prior prob‑ability

(

|

b

)is given by

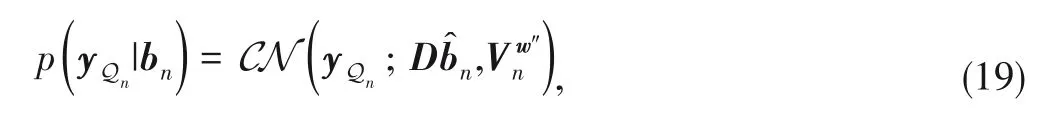
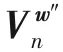
Near his house stood the ancient barn that housed the family s goats and chickens. Reuben found a rusty6 soda7 tin and dropped his coins inside. Then he climbed into the loft8 of the barn and hid the tin beneath a pile of sweet smelling hay.

3.2 Factor Graph Representation

Let Q(⋅)represent the 1-bit quantization function.The re‑sulting quantized signal

is given by

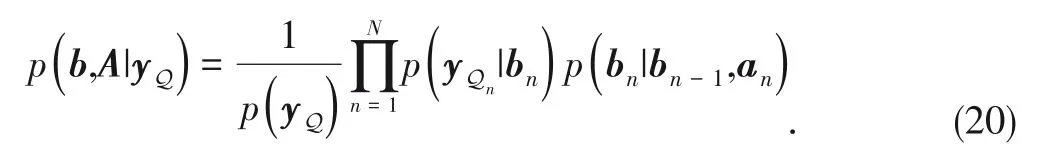
Defining

≜(

⊙

)∈C

in Eq.(10),the joint poste‑rior probability can be further factored as

56. Carry us across separately: Gretel appears to have achieved a new maturity131 with her defeat of the witch. She no longer needs to hold Hansel s hand, but can cross the lake separate from him. This also shows that she is thinking beyond her own needs and considering the abilities of someone--or something--else. She does want to overburden the duck, a compassionate132 thought when she has had few previously133.Return to place in story.

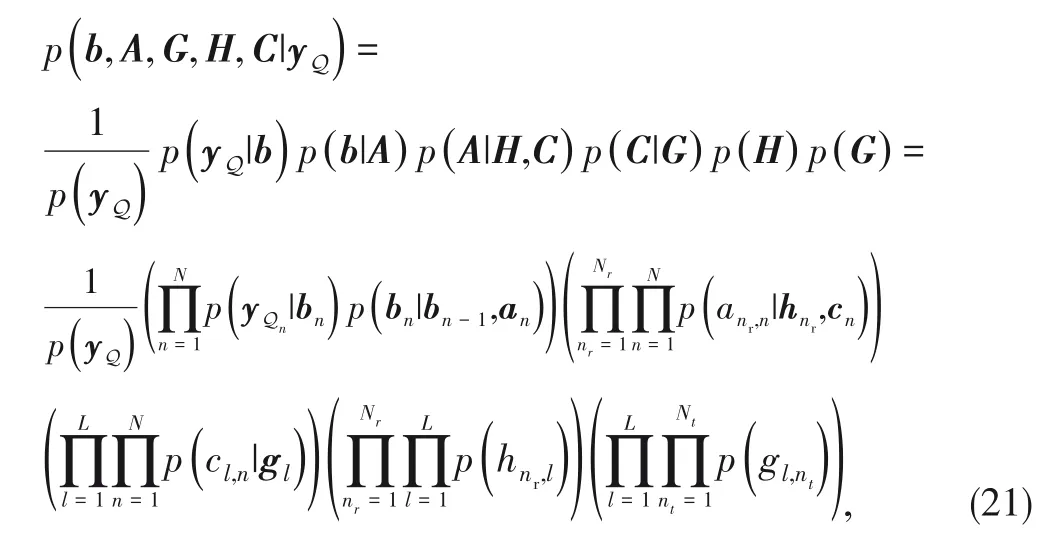
where the first bracket is from the Markov chain and the rests belong to the bilinear structure described in Ref]13].Some involved probabilities are

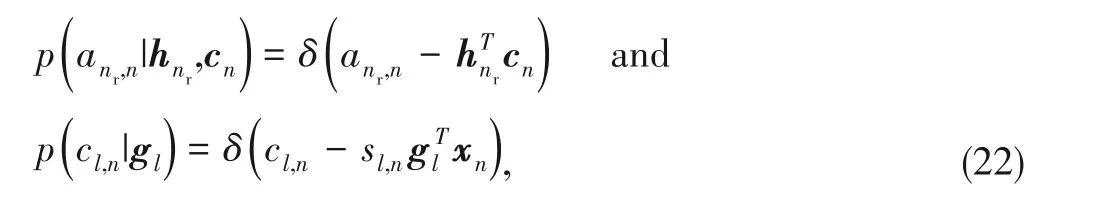
where

h

∈C

and

g

∈C

are the

-th and

-th row of

and

,respectively;

c

∈C

is the

-th column of

.The second formula in Eq.(22) comes from the definition of

,where

c

and

s

are the(

,

)-th element of

and

,respec‑tively,and

x

is the

-th column of

.The factor graph repre‑sentation of Eq.(21) is shown in Fig.2,where the hollow circles and the solid squares represent the variable nodes and the factor nodes,respectively.The message passing in the first part will be described in the next subsection,while the illus‑tration of the second part can be found in Ref]8].

3.3 Message Passing in Markov Chain

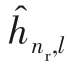
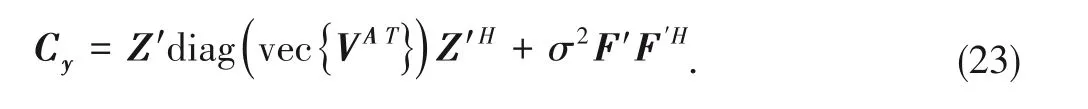
The system model of Eq.(11) can be decomposed by using the Bussgang theorem

:

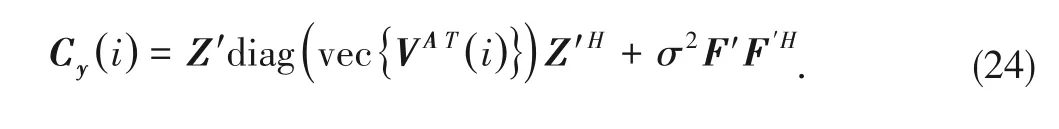
And he swirled22 Medio Pollito over the roofs of the houses till they reached the highest church in the town, and there he left him fastened to the top of the steeple

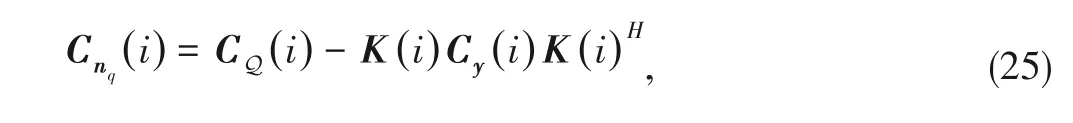
where

(

)is calculated from Ref]16]as

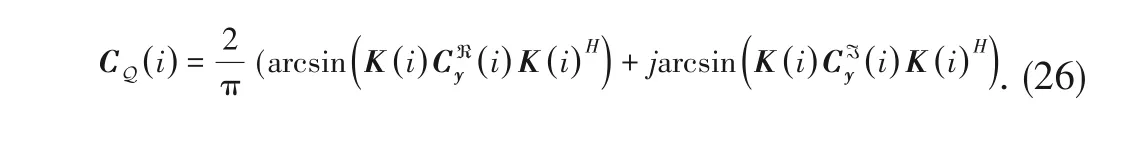
3.3.1 Downward AMP

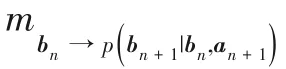
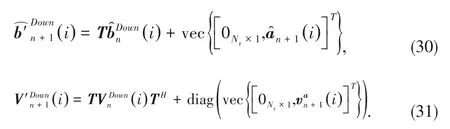
Especially,when

=1,Eqs.(30)and(31)are reduced to

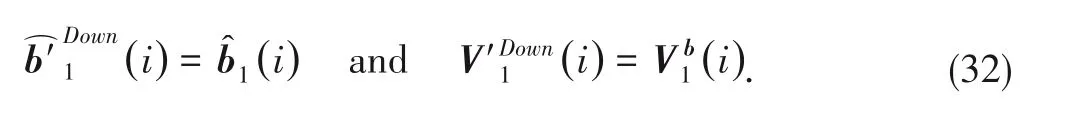
3.3.2 Upward AMP

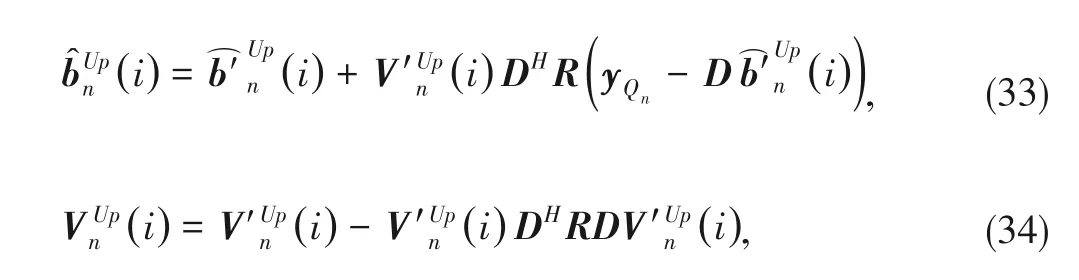
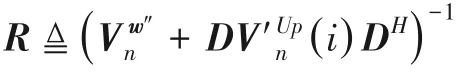
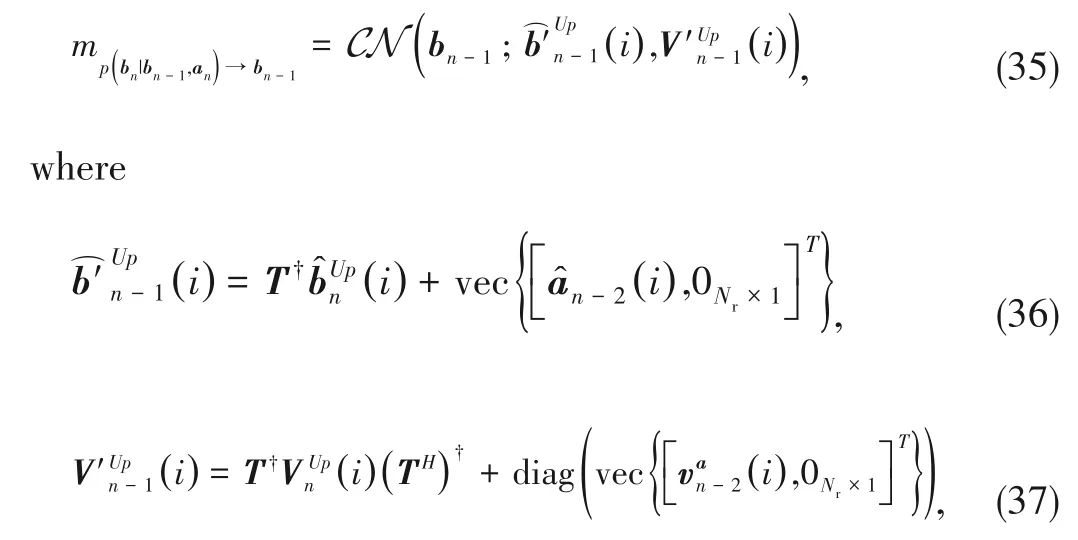
where (⋅)

denotes the operation of pseudo-inverse.Espe‑cially,when

=

,Eqs.(36)and(37)are reduced to

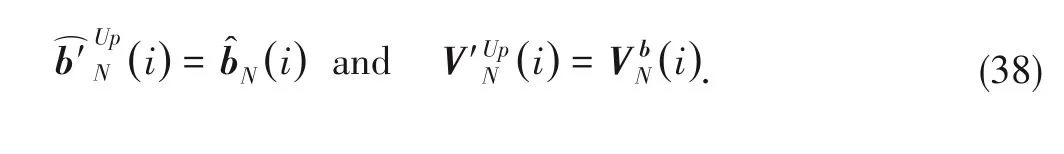
3.3.3 Backward AMP

The covariance of the quantization noise at the

th it‑eration is

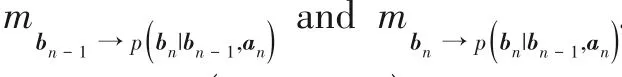
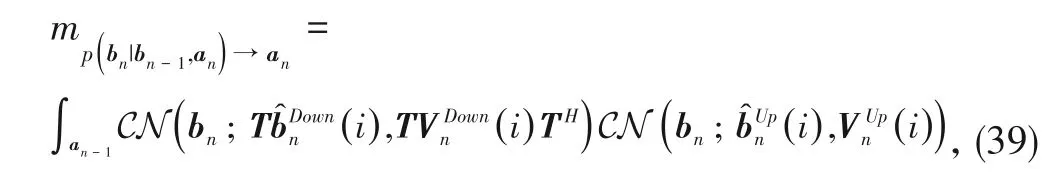
where the multiplication of two Gaussian functions is another Gaussian function

.

When the birds began to sing he could lie still no longer, and climbed out of his window into the branches of one of the great lime-trees that stood before the door

Tsarevitch Ivan got down, and having bade the Wolf farewell with tears, entered the city and went at once to the Palace, where the Tsarevitch Vasilii was even then being wed to Helen the Beautiful.

4 Further Discussions

In the following,the approximate message passing in the Markov chain is derived according to the sum-product rule.The linear operator

described in Eq.(17) involves the cova‑riance of unquantized signal

in Eq.(10),calculated as

where

∈[0,1]is the damping factor.In our work,

is cho‑sen within[0.2,0.4].

But he forgot that to go back absent, and dreamy, and indifferent, when he had before been gay and ardent11 about everything, was the surest way of awakening12 suspicion; and when, in response to the jesting questions which were put to him upon the subject, he only blushed and returned evasive answers, all the ladies were certain that he had lost his heart, and did their utmost to discover who was the happy possessor of it

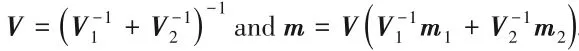
Markovian cascaded channel estimation

5 Numerical Results

where the elements of

' and

' are independent and identi‑cally distributed (i.i.d.) complex Gaussian random variables with zero mean and unit variance.The matrix

denotes the receive correlation matrix with the following form:

The witch s cottage is one of the more popular elements in illustrations of the tale. To see several illustrators visions of the house, visit the Illustrations of Hansel and Gretel page.Return to place in story.

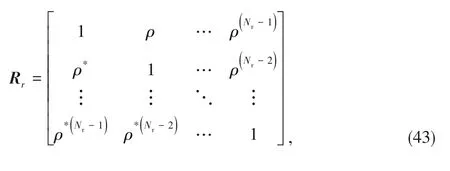
where

is the correlation index of neighboring antennas at the BS and set as 0.4+0.3

.(|

|=0 represents an uncorre‑lated scenario and |

|=1 implies a fully correlated sce‑nario.) The matrices

and

have the same form as Eq.(43),where

is set as 0.2+0.5

and 0.1+0.2

at the RIS,re‑spectively.

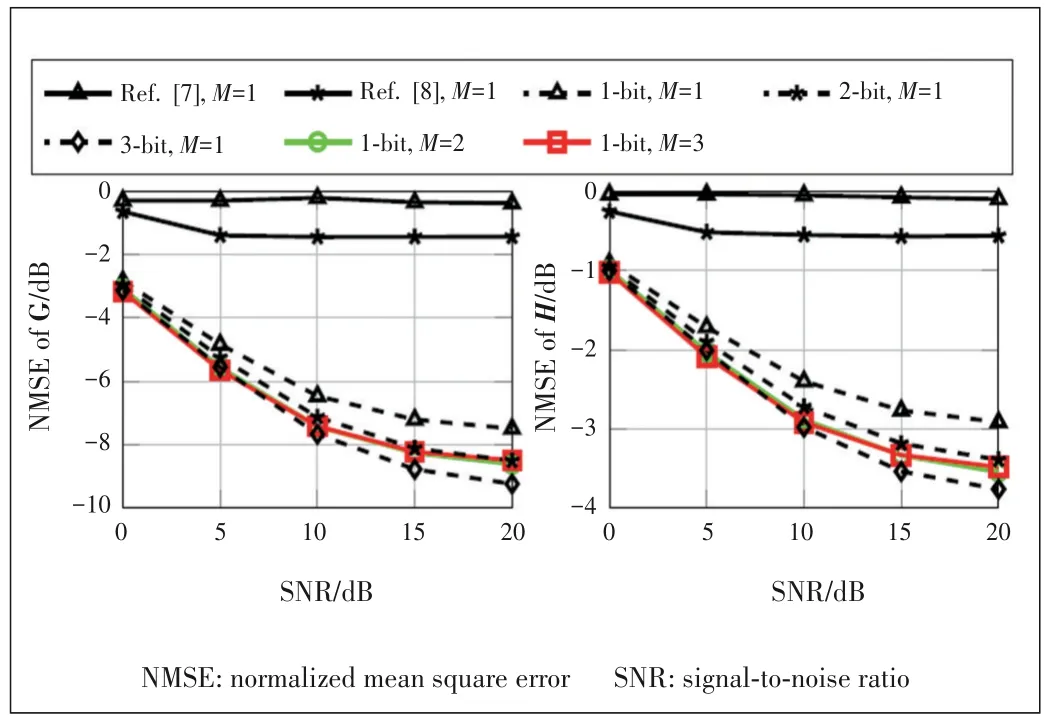
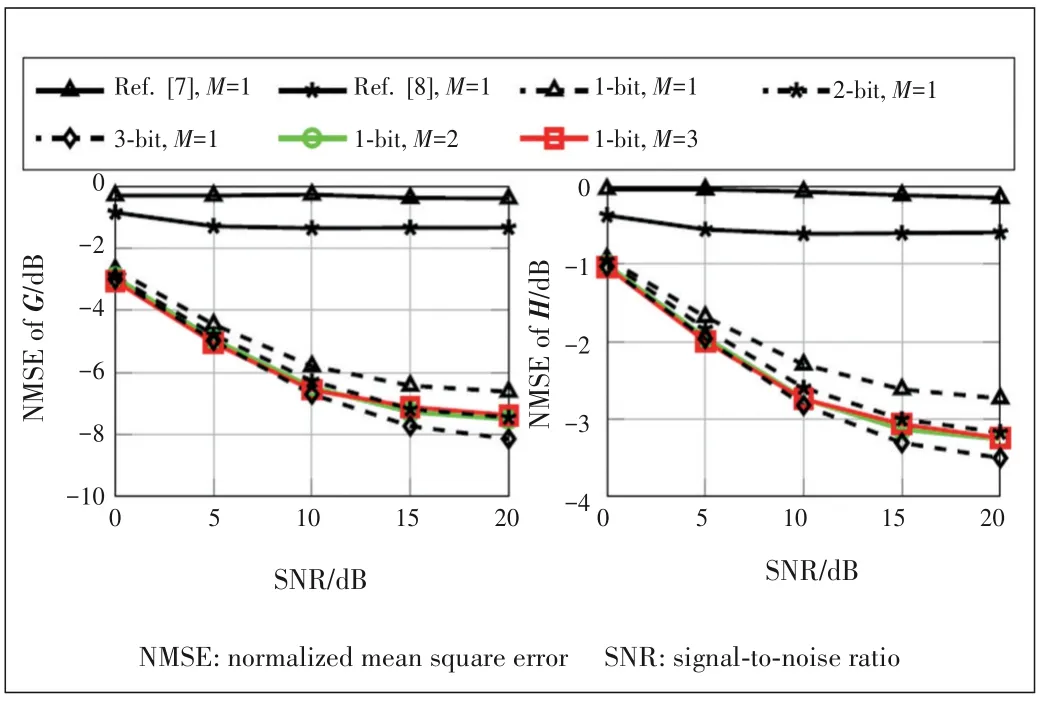
Figs.3 and 4 show the NMSEs of

and

under uncorre‑lated and correlated channels,respectively.For the multi-bit systems sampling at the Nyquist rate,the calculation of the posterior probability

(

|

y

) is referred to as Eqs.(23) and(24) in Ref]17].From the figures,it can be seen that our proposed 1-bit multi-fold oversampled systems outperform 1-bit systems sampling at the Nyquist rate,and can even ap‑proach the performance of 2-bit systems sampling at the Ny‑quist rate.Another observation is that after 2-fold oversam‑pling,the performance of 1-bit systems goes into the satura‑tion field,and no further gain can be achieved.This reveals the performance limit of the proposed method.Furthermore,we have also compared the performance of Refs]7] and [8]as references,where the resolutions of the ADCs are changed to 1-bit.From the results,the performance of the references is worse than that of our proposed method,since they do not consider the impact of 1-bit quantization and the advantages of oversampling.

After riding for a day and a night, almost without stopping, he came to a great cave where he made the woman dismount, and, taking her and the baby into the cave, he drew his sword and with one blow chopped her head off

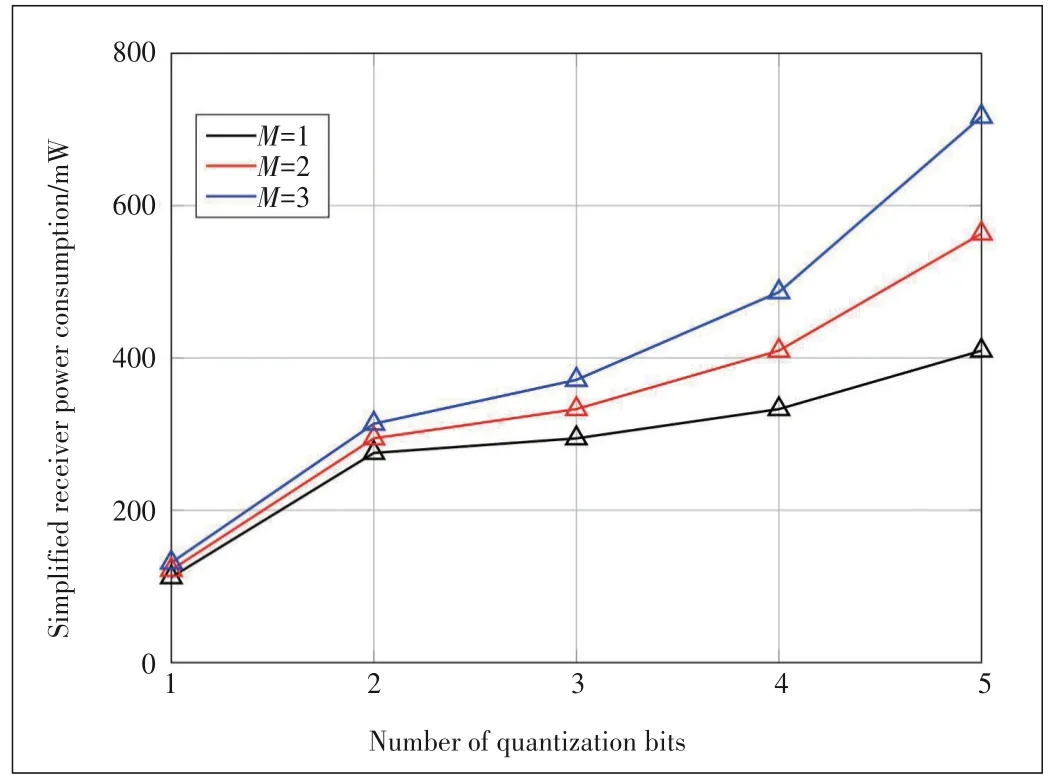
The advantage of 1-bit ADCs is that they do not require au‑tomatic gain control (AGC),and can be replaced by simple LAs.Fig.5 shows the simplified

receiver power consumption as a function of the quantization bits and the oversampling fac‑tor

,which is calculated as

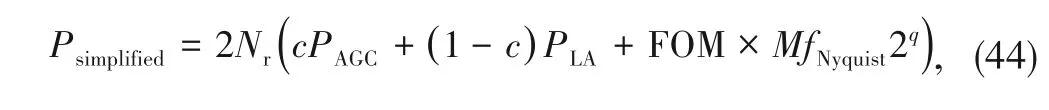
where

and

denote the power consumption of AGC and LA,respectively;

is the quantization bits and

is the Nyquist-sampling rate;

is chosen as 0 for 1-bit system and 1 for systems with multi-bit.Numerical parameters

are

=2 mW,

=0.8 mW,

=2.5 GHz and figures-of-merit (FOM)=15 fJ.From the results,it can be seen that 1-bit systems consume much less power than multi-bit systems with either the Nyquist rate or the overs‑ampling rate.

One cold evening during the holiday season, a little boy about six or seven was standing1 out in front of a store window. The little child had no shoes on and his clothes were mere2 rags. A young woman passing by saw the little boy and could read the longing3 in his pale blue eyes. She took the child by the hand and led him into the store. There she bought him new shoes and a complete suit of warm clothing.They came back outside into the street and the woman said to the child, “Now you can go home and have a very happy holiday.”The little boy looked up at her and asked, “are you God, Ma’am?”She smiled down at him and replied, “No son, I’m just one of His children.”The little boy then said, “I knew you had to be some relation.”

6 Conclusions

In this work,we propose RIS aided 1-bit massive MIMO systems with oversampling at the receiver.The aim of oversampling is to compensate for the performance loss due to the coarse quantization.A Markovian cascaded channel estimation algorithm is developed for such sys‑tems.Simulation results have shown good performance gains of the proposed oversampled system,which can achieve the same performance of the corresponding 2-bit system sampling at the Nyquist rate while consuming less power at the receiver.

[1]LARSSON E G,EDFORS O,TUFVESSON F,et al.Massive MIMO for next gen‑eration wireless systems [J].IEEE communications magazine,2014,52(2):186-195.DOI:10.1109/MCOM.2014.6736761

[2]LIASKOS C,NIE S,TSIOLIARIDOU A,et al.A new wireless communication paradigm through software-controlled metasurfaces [J].IEEE communications magazine,2018,56(9):162-169.DOI:10.1109/MCOM.2018.1700659

[3]JAMALI V,TULINO A M,FISCHER G,et al.Intelligent surface-aided trans‑mitter architectures for millimeter-wave ultra massive MIMO systems [J].IEEE open journal of the communications society,2020,2:144-167.DOI:10.1109/OJCOMS.2020.3048063

[4]TAHA A,ALRABEIAH M,ALKHATEEB A.Enabling large intelligent sur‑faces with compressive sensing and deep learning [J].IEEE access,2021,9:44304-44321.DOI:10.1109/ACCESS.2021.3064073

[5]ARDAH K,GHEREKHLOO S,DE ALMEIDA A L F,et al.TRICE:A channel estimation framework for RIS-aided millimeter-wave MIMO systems [J].IEEE signal processing letters,2021,28:513 -517.DOI:10.1109/LSP.2021.3059363

[6]HE Z Q,YUAN X J.Cascaded channel estimation for large intelligent metasur‑face assisted massive MIMO [J].IEEE wireless communications letters,2020,9(2):210-214.DOI:10.1109/LWC.2019.2948632

[7]WANG P L,FANG J,DUAN H P,et al.Compressed channel estimation for in‑telligent reflecting surface-assisted millimeter wave systems [J].IEEE signal processing letters,2020,27:905-909.DOI:10.1109/LSP.2020.2998357

[8] HE Z Q,LIU H,YUAN X J,et al.Semi-blind cascaded channel estimation for reconfigurable intelligent surface aided massive MIMO [EB/OL]]2021-11-15].https://arxiv.org/abs/2101.07315

[9]WALDEN R H.Analog-to-digital converter survey and analysis [J].IEEE jour‑nal on selected areas in communications,1999,17(4):539-550.DOI:10.1109/49.761034

[10]MO J H,HEATH R W.Capacity analysis of one-bit quantized MIMO systems with transmitter channel state information [J].IEEE transactions on signal pro‑cessing,2015,63(20):5498-5512.DOI:10.1109/TSP.2015.2455527

[11]LI Y Z,TAO C,SECO-GRANADOS G,et al.Channel estimation and perfor‑mance analysis of one-bit massive MIMO systems[J].IEEE transactions on sig‑nal processing,2017,65(15):4075-4089.DOI:10.1109/TSP.2017.2706179

[12]SHAO Z C,DE LAMARE R C,LANDAU L T N.Iterative detection and decod‑ing for large-scale multiple-antenna systems with 1-bit ADCs [J].IEEE wire‑less communications letters,2018,7(3):476 -479.DOI:10.1109/LWC.2017.2787159

[13]SHAO Z C,LANDAU L T N,DE LAMARE R C.Channel estimation for largescale multiple-antenna systems using 1-bit ADCs and oversampling [J].IEEE access,2020,8:85243-85256.DOI:10.1109/ACCESS.2020.2992246

[14]SHAO Z C,LANDAU L T N,DE LAMARE R C.Dynamic oversampling for 1-bit ADCs in large-scale multiple-antenna systems [J].IEEE transactions on communications,2021,69(5):3423 -3435.DOI:10.1109/TCOMM.2021.3059303

[15]BUSSGANG J J.Crosscorrelation functions of amplitude-distorted Gaussian signals[R].Cambridge,USA:Massachusetts Institute of Technology,1952

[16]JACOVITTI G,NERI A.Estimation of the autocorrelation function of complex Gaussian stationary processes by amplitude clipped signals [J].IEEE transac‑tions on information theory,1994,40(1):239-245.DOI:10.1109/18.272490

[17]WEN C K,WANG C J,JIN S,et al.Bayes-optimal joint channel-and-data esti‑mation for massive MIMO with low-precision ADCs [J].IEEE transactions on signal processing,2016,64(10):2541 -2556.DOI:10.1109/TSP.2015.2508786

[18]ROTH K,NOSSEK J A.Achievable rate and energy efficiency of hybrid and digital beamforming receivers with low resolution ADC [J].IEEE journal on se‑lected areas in communications,2017,35(9):2056-2068.DOI:10.1109/JSAC.2017.2720398