融合可链接环签密的智能合约电子投票协议
王杰昌,张 平,高 远,刘玉岭
(1.郑州大学体育学院 体育大数据中心,郑州 450000;2.河南科技大学 数学与统计学院,河南 洛阳 471023;3.国网三门峡供电公司,河南 三门峡 472000;4.中国科学院 信息工程研究所,北京 100190)
0 概述
区块链技术[1]具有去中心化[2]、公开透明、可追溯[3]等诸多优点,无需任何可信中心即可在陌生网络节点间搭建可信的价值传递渠道,可广泛应用于医疗、物联网等各个领域[4]。区块链2.0 以以太坊为代表实现了更复杂的分布式合约记录——智能合约[5],虽然智能合约的概念早在1994 年就被提出[6],但直到近年来得益于区块链技术的发展,其利用价值才被逐步发掘。
电子投票是一种新型网络投票系统,较传统方式更具经济性,其使用密码学确保投票过程公正、公平、公开、透明[7]。它所用到的密码学知识主要包括环签名、同态加密、混合网络、零知识证明等,其中环签名[8]是一种简化的群签名,只有环成员、没有管理者,无需环成员之间的合作,对验证者来说签名者完全是匿名的。可链接环签名[9-11]是指若某个环成员产生2 个消息签名对,存在有效算法使得签名验证者可以确定这2 个消息签名对是由环中同一成员产生的[12-13]。
为同时确保数据的机密性和可认证性,传统方法通常对数据进行先签名后加密或者先加密后签名的操作,这类方法的计算量和通信成本是加密和签名的代价之和。而签密[14]在一个逻辑步骤内实现加密和签名,也能达到传统方法的效果,同时具有以下优点:低于传统方法的计算量及通信代价;允许部分高代价密码运算的并行计算;若设计恰当可更安全;简化了同时需要认证性与机密性的密码算法设计[15]。
ZHAO 等[16]在电子投票方案中应用区块链技术,但该方案只支持2 个候选者。MCCORRY 等[17]提出使用智能合约实现的开放投票协议,但该协议使用的前提是不能出现投票者弃权的情况,不切实际。BISTARELLI 等[18]提出一个基于比特币的端到端投票系统,充分保护投票者的隐私,但该系统过于集中,方案不够公开透明。ZHEGN 等[7]提出一个以太坊电子投票方案,利用一次性环签名及匿名地址技术,解决了部分投票隐私性等问题,但缺乏安全性证明和仿真实验。LYU 等[19]设计一个基于智能合约的去中心化、无信任的电子投票系统,在投票阶段对其选票加密后进行环签名,确保了投票结果的可信度,解决了投票过程中的部分安全问题,但该系统没有任何安全性证明,且计算消耗的gas 较多,运行时间较长。
针对上述问题,本文通过构造可链接环签密,提出一个基于智能合约的电子投票协议,并在一个逻辑步骤内实现选票的加密和签名,在确保协议具有相关安全特性的同时,从总体上降低协议运行时间和计算消耗的gas。
1 预备知识
1.1 选择消息的环分叉引理
引理1选择消息的环分叉引理[20]。∑ring为一般的环签名方案,k为安全参数,n为环成员数量。A为一个概率多项式时间的图灵机,输入仅包含公共参数,Q和W分别表示A询问随机预言机的次数以及询问一些真实环签名者的次数。假设A在时间T内,以不可忽略的优 势ε≥生成一个有效的环签名(m,R1,…,Rn,h1,…,hn,σ),其 中VQ,n=Q×(Q-1)×…×(Q-n+1)。假定在不知道任何环密钥的情况下,有效的环签名在时间Ts内能以不可区分的概率被模拟,那么就存在另一个概率多项式时间的图灵机,通过模拟替代与真实签名者的交互从A中获得对机器的控制权,在预期的时间T′≤内生成2 个有效的环签名(m,R1,…,Rn,h1,…,hn,σ)和(m,R1,…,Rn,′,σ′)。其中:对于某个j∈{1,2,…,n},hj同时,对于所有的i=1,2,…,n(i≠j),hi=
1.2 椭圆曲线上的离散对数问题
在椭圆曲线构成的阿贝尔群Ep(a,b)上考虑方程Q=k×P,其中P,Q∈Ep(a,b),k<p,由k和P容 易求得Q,但由P和Q求k较困难,这就是椭圆曲线上的离散对数问题[21]。
1.3 无可信中心的门限加密
在门限加密系统[22-24]中,加密组的n个成员共享一对系统公私钥,所有的成员都知道系统公钥,然而在无可信中心[25]参与的情况下,系统私钥分成若干个秘密份额,每个秘密份额由1 个成员保存,最少需要t名成员才能重构系统私钥。
群{Pi|i∈[1,n]}包含n个成员,Fp表示阶为p且生成元为g的有限循环群,门限值k是重构私钥的最小人数。无可信中心的门限加密具体步骤如下:
1)群Pi随机选择xi∈Fp,计算hi=,公钥h是所有hi之和。
2)群Pi随机选择一个度至多为k-1 且fi(0)=xi的多项式fi(c)∈Zq(c),fi(c)=fi+fi1c+…+fi,k-1ck-1,Pi计算Fij=,其中j=0,1,…,k-1。
3)当每位成员公布这些k值后,Pi秘密地将sij=fi(j)发送给Pj,其中j=1,2,…,n。
4)使用Pi验证从Pj处得到的sij,为了确保和先前公布的值一致,Pj计算若不成立,则中止。
5)Pi计算 其份额si并作为x的 一份,f表 示多项式f(c)=f1(c)+f2(c)+…+fn(c),si为f(0)=x的一份,通过构建si=f(i),使其能够很容易地重构出系统私钥x。
2 系统模型及区块链结构
2.1 系统模型
系统模型使用三元组<admin,users,contract >表示,包含3 个实体:投票管理员,投票者和智能合约,如图1 所示,该3 个实体的具体描述如下:
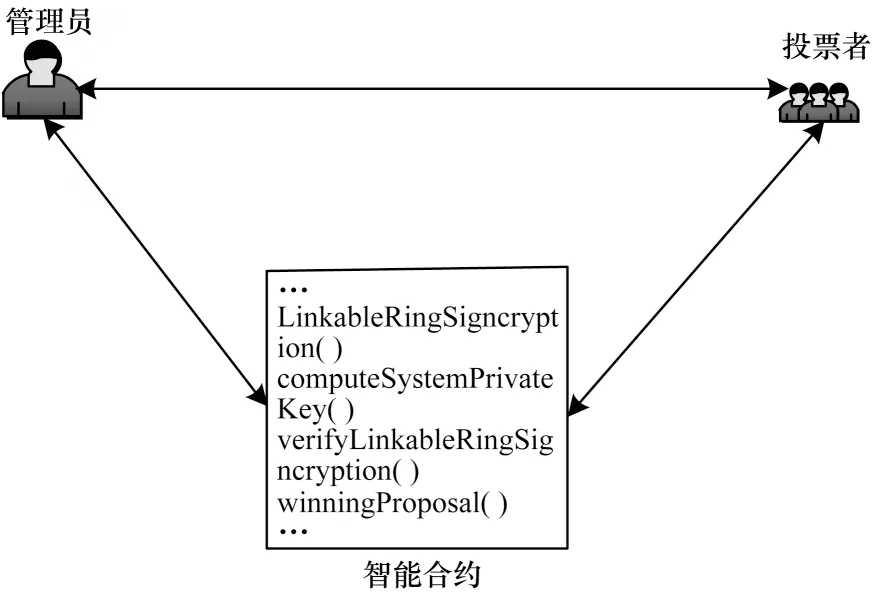
图1 电子投票模型Fig.1 E-voting model
1)投票管理员(admin):创建投票进程,编写投票合约代码;通过公钥参数鉴定投票者的资格;公布投票者公钥列表、投票问题及候选项;设定并公布投票相关时间节点(注册截止时间tfr、投票者上传密钥参数截止时间tfg、开始投票时间tbν、结束投票时间tfν、投票者上传秘密份额开始时间tbss、投票者上传秘密份额截止时间tfss、公布投票结果时间tp);发起创建投票智能合约请求。
2)投票者users:Ui为投票者之一,具有以太坊账户和公私钥对,在预设的时间节点前完成注册和投票。
3)智能合约contract:智能合约并不是协议中的真正实体,但所有实体都与智能合约进行交互,故将其定义为“虚拟实体”;其由投票管理员admin 请求创建,包括可链接环签密函数LinkableRingSigncryption()、计算系统私钥函数computeSystemPrivateKey()、验证环签密函数verifyLinkableRingSigncryption()、计票函数winningProposal()等,其具有的功能包括:按照admin编写的总体投票流程运行、检验所接收的消息是否来自合法的Ui、保存门限加密的有关信息、重构系统私钥、解密选票并验证签密、统计有效选票并公布获胜提案等。
2.2 投票区块链结构
区块链的结构如图2 所示,主要包括合约创建交易、上传参数交易、合约调用交易被打包进区块并加入区块链。

图2 投票区块链结构示意图Fig.2 Schematic diagram of voting blockchain structure
上述交易的上链过程为:
1)合约创建交易。投票管理员admin 发起创建电子投票智能合约请求,内容包括发送账户地址(即admin 账户地址)、接受账户地址(为0,表示该交易为创建智能合约的交易)、本次转移的以太币数量、用于完成交易的gas 数量、承诺支付的gas 单价等;接着,网络节点验证交易请求,并争取到打包权的矿工,遵循admin 发送的交易费用与合约代码,创建合约账户,在账户空间中部署合约,同时将智能合约账户地址返回给admin,并将admin 的请求打包进区块,全网传播该区块,令区块加入共识区块链。
2)上传参数交易。投票者Ui发起上传参数交易请求,内容包括投票者用户地址、接收账户地址(admin 创建的智能合约账户地址)、本次转移的虚拟货币数量、用来完成交易的gas数量、交易中愿意付出的gas单价、发送给接收地址的消息(密钥参数、秘密份额、选票签密等);接着,网络节点验证交易请求,交易被矿工打包进区块,并将区块加入共识区块链。
3)合约调用交易。在需要计算系统私钥、验证签密、计票时,admin 发起合约调用交易请求,交易内容包括发送账户地址、接收合约账户地址、本次转移的“虚拟货币”数量、用来完成交易的gas 数量、交易中愿意付出的gas 单价、执行智能合约或其某功能函数的指令,该请求被传播到区块链上;接着,网络节点验证交易请求,争取到打包权的矿工将在本地节点运行被调用的合约代码,直至代码运行结束或gas消耗殆尽后,将该区块加入本地区块链,并在全网传播该区块,令区块加入共识区块链。
3 本文智能合约电子投票协议
本文协议将已有协议中选票的“加密+环签名”方式改进为选票的可链接环签密,在保证安全性的同时,降低协议运行时间和计算消耗的gas。同时因签密是在一个逻辑步骤内实现了解密和签名验证,本协议将选票签密的验证放至最后的计票阶段,而非像已有投票协议那样在投票阶段验证签名。改进后,本协议分为注册、创建、密钥生成、投票、秘密份额上传、计票6 个阶段,G是阶为l的椭圆曲线E的基点。
3.1 注册阶段
每一个投票者Ui根据公共参数计算自己的公私钥对(yi,xi),其中:yi=xiG;xi∈(为了方便起见,本文中类似xiG的表达式,皆表示取xiG的纵坐标值),admin 对投票者进行认证,收集通过认证的Ui(i∈[1,n])的公钥yi(i∈[1,n])并组成公钥列表,设定门限密钥重构的最小份额数为k。
3.2 创建阶段
admin 设定一个时间节点列表来触发相应的投票进程,然后将公钥列表、时间节点、整体投票进程等写入合约代码,发出智能合约创建请求。在合约创建后,admin 将智能合约账户地址及其他相关信息公布。
3.3 密钥生成阶段
每一个投票者Ui随机选择λi∈Fq,并且计算ηi=λiG,Ui按如下方法分发λi:
1)投票者Ui随机选择一个阶为k-1 的多项式,如式(1)所示:
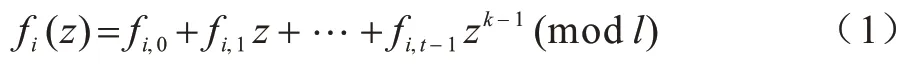
其中:fi(0)=fi,0=λi。
2)投票者Ui首先计算Fi,j=fi,jG(其中j=0,1,…,k-1),并利用私钥xi对(Fi,j,i,j)签名后发起上传密钥参数请求,然后公钥参数被矿工上传至admin 创建的智能合约账号,智能合约利用公钥yi列表验证签名是否合法,若合法则保存该信息作为合约参数,否则丢弃。投票者Ui计 算其 中j=1,2,…,n。接着,投票者Ui用xi对(si,j,i,j)签名后发起上传请求,然后(si,j,i,j)及其签名被矿工上传至admin 创建的智能合约账号,智能合约验证签名,若合法则保存该信息作为合约参数,否则丢弃。投票者必须在tfg之前完成这些计算及发送工作。
这里,每位投票者均可获得所有的si,j和Fi,j,投票者Ui可 通过xi计算并获得系统公钥η通过式(2)进行计算:
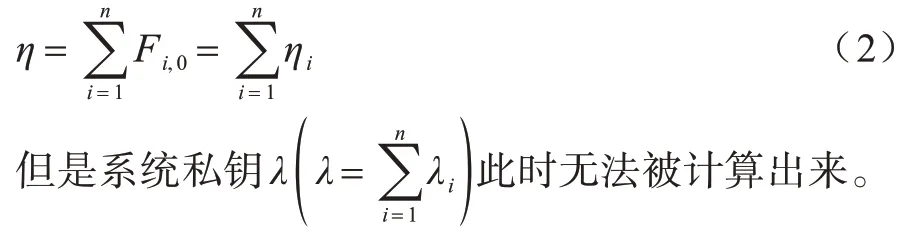
3.4 投票阶段
投票者Ui根据编码规则及自己的选择生成选票Vi,然后投票者Us(1≤s≤n)利用LinkableRingSigncryption()对其选票Vs进行可链接环签密。
3.4.1 签密初始化
H1:{0,1}*→Zq和H2:{0,1}*→Fq是2 个安全的哈希函数,环中有n个成员,即U={U1,U2,…,Un}。投票者Ui(i∈[1,n]) 的公私钥对为(yi,xi),其中yi=xiG,G∈E。
3.4.2 签密生成
签密生成的步骤如下:
1)投票者Us计算θ=H2(y1,…,yn),t=xs×θ;
2)对于i∈{1,2,…,n},i≠s,随机选择互不相同的ai∈,计算Ri=aiG;
3)随机选取a∈Zq,计算Rs=
4)计算σ=
5)投票者Us计算
6)计 算hi=H1(Vs,Ri,t),i=1,2,…,n,生成签密Ω=
3.4.3 选票上传
投票者发出上传选票签密Ω 请求,矿工将签密Ω 上传至区块链上admin 创建的智能合约账号,作为计票阶段成员函数调用的参数,投票者必须在tfν之前完成本阶段工作。
3.5 秘密份额上传阶段
投票者Ui根据式(3)对其之前获得的进 行验证。


Ui发起秘密份额上传请求,同时(si,i)及其对应的签名被矿工上传至admin 创建的智能合约账号,且投票者必须在tfss之前完成上传工作。
3.6 计票阶段
当至少有t名投票者上传秘密份额时,智能合约中的函数computeSystemPrivateKey()通过式(5)计算获得系统私钥:
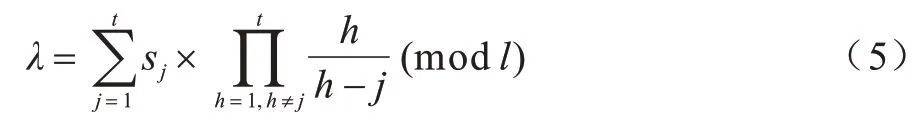
对智能合约中的验证环签密函数verifyLinkableRingSigncryption()进行如下操作:
1)有任意2 个环签密:

由于部署在区块链上的智能合约式是公开透明的,无法篡改,因此在区块链上进行电子投票,同时也可以确保投票公开、公正、公平。
4 安全性分析
4.1 正确性
本文仅论证选票签密及验证的正确性,根据式(6)进行验证:

当式(6)所示的验证方程成立时,选票签密有效。
4.2 不可伪造性
引理2在随机预言机模型下,若椭圆曲线离散对数问题是困难的,则环签名Ω′是不可伪造的。

定理1若椭圆曲线离散对数问题是困难的,则本协议的环签密是不可伪造的。
证明:假设某用户能伪造合法的投票环签密,那么其肯定可以利用环签名的转换算法,将伪造的环签密转换成环签名,即在椭圆曲线离散对数问题是困难的情况下,得到一个伪造的环签名。这显然与引理1 相矛盾,定理得证。
4.3 隐私性
本节着重探讨Ui和Vi的隐私。从Ui隐私方面来说,由于可链接环签名的特性,在具有n个元素的公钥环上进行的环签名,任意环外的攻击者确定出真正签名者的概率不超过如果攻击者为环内某一非签名者,那么其不能以大于的概率确定出真正的签名者。从Vi隐私的方面来说,任何人都无法在3.6 节以前解密选票。
4.4 唯一性
本文设计的投票协议采用可链接环签密,其可链接性能够确保一位投票者只可投一次票,若重复投票将被验证出来,则作废处理,以保证协议的唯一性。
4.5 公正性
本文协议融合了无可信中心的门限加密、可链接环签密及智能合约,在3.6 节以前,投票者只掌握其本人的投票内容,任何人都不可能获取中间结果或最终结果,以确保本协议的公正性。
4.6 可验证性
选举结束后,任何投票者均可查看选票及系统私钥,以查看自己的选票是否被正确记录,且拥有合约地址的任何人均可查看所有选票并验证计票结果。
5 性能评估
5.1 性能分析
选票签名或签密的可链接性都将被进行验证,这一点对于本文协议和Lyu 协议来说没有差别。但是对于加密选票签名,Lyu 协议需要在投票阶段和计票阶段分别进行验证和解密,而本文协议在3.6 节计票阶段第2 步的一个逻辑步骤内实现了选票签密的验证和解密,降低了计算量,进而降低了gas 消耗,最终gas 消耗总量也随之降低。
在电子投票协议中,除了选票的验证、统计等工作由智能合约完成外,仍有很多操作需要投票者运行,包括生成公私钥、计算Fi,j与fi(j)、验证来自其他投票者的fj(i)、计算系统公钥、恢复秘密份额、生成选票签名或签密等操作。对于生成公私钥、计算Fi,j与fi(j)、验证来自其他投票者的fj(i)、计算系统公钥、恢复秘密份额等操作,两协议没有差别。但是Lyu 协议需要对选票进行加密后才能签名,而本文协议生成了选票签密,在一个逻辑步骤内实现了签名和加密,降低了计算量和运行时间,进而操作总时间也随之降低。
5.2 仿真实验
本文在本地部署以太坊私有网络,通过truffle将智能合约部署到以太坊私有网络上,同时进行挖矿并确认交易。本文协议从确认交易的信息中获得交易消耗的gas,投票者或管理员可以在rpc 模式使用web3.js 与区块链网络进行通信。
本地投票计算机配置为Win10系统,四核2.9 GHz的CPU,8 GB 内存。系统中的功能函数均用Python编写,所有时间单位均为ms,每gas的价格定为1 Gwei,在t=0.7n的情况下进行测试。
5.3 gas 消耗
表1 展示了在n=30 的情况下投票者和管理员每个交易的gas 消耗,其中,由管理员admin 发起的交易只发起一次,由投票者Ui发起的交易每名一次。
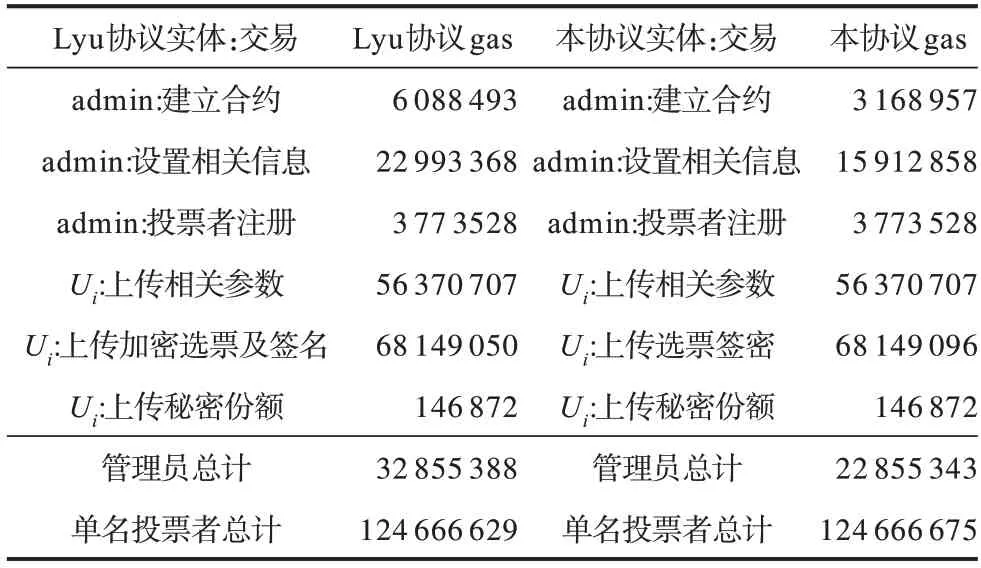
表1 交易或计算的gas 消耗Table 1 Consumption of transaction and computation in gas
对比本文协议与Lyu 协议,从表1 可看出投票者上传数据至区块链的gas 消耗基本一样,而本文协议admin 建立合约及设置相关信息的gas 消耗要低于Lyu 协议的消耗。这是因为Lyu 协议中智能合约执行的是选票环签名验证函数和加密选票解密函数,而本文协议中智能合约执行的是选票签密的验证(解密)函数,能够在一个逻辑步骤内实现验证和解密;同时,Lyu 协议及本文协议执行这些功能函数所消耗的gas 均包含在admin 建立合约及设置相关信息交易中。
为研究选举时各实体的gas 消耗与投票者人数之间的关系,分别对n=10、20、30、40 的情况进行测试,再利用python 画出两协议不同实体的gas 消耗对比图,结果如图3 所示。
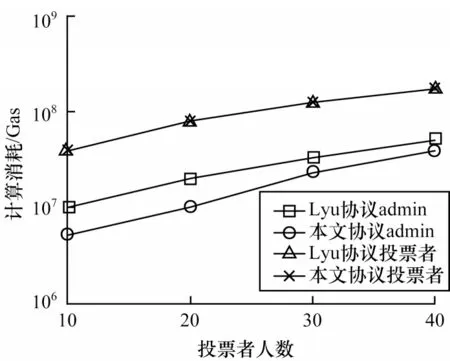
图3 本文协议与Lyu 协议的gas 消耗对比Fig.3 Comparison of gas consumption between this protocol and Lyu protocol
从图3 可以看出,随着投票者人数的增加,本文协议和Lyu 协议中admin 和投票者的交易或计算消耗的gas 都在增加。但是无论投票者人数如何变化,本文协议投票者的gas 消耗和Lyu 协议投票者的基本一样,本文协议admin 的gas 消耗始终要比Lyu 协议admin 的低,降低了约1×107gas,每gas 的价格为1 Gwei,即节省了1×107Gwei 的计算消耗,其原因与n=30 的情况一样,所以最终本文协议的gas 消耗总量低于Lyu 协议的gas 消耗总量。
5.4 操作运行时间
表2 展示了在n=30 时在投票者本地运行的操作所花费的时间。
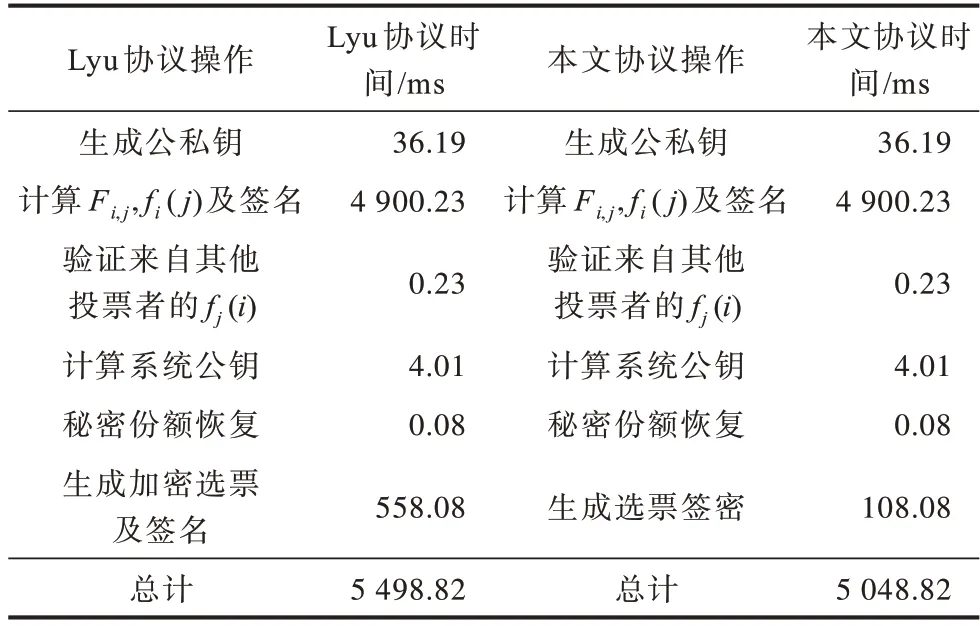
表2 投票者操作运行时间Table 2 Voter operation run time
从表2 可以看出本文协议与Lyu 协议在投票者本地运行的生成公私钥、计算Fi,j与fi(j)及签名、验证来自其他投票者的fj(i)、计算系统公钥、恢复秘密份额等所花费的操作时间都一样,但本协议投票者生成选票签密的时间要低于Lyu 协议投票者生成加密选票及签名的时间,这是由签密的性质决定的。另外,当n=30 时本文协议投票者本地运行的操作总时间也低于Lyu 协议所花费的时间。
对投票者运行的操作总时间进行测试并统计,再利用python 绘制出本文协议与Lyu 协议在这方面的对比图,结果如图4 所示。

图4 本文协议与Lyu 协议投票者的操作总时间对比Fig.4 Comparison of total voter operation time between this protocol and Lyu protocol
由图4 可知,随着投票者人数的增加,本协议和Lyu 协议中投票者运行的操作总时间均在增加,但是无论投票者人数如何变化,本文协议投票者的操作总时间始终比Lyu 协议的低,少了约450 ms,其原因与n=30 时的情况相同。
6 结束语
本文提出一种新的智能合约电子投票协议,融合可链接环签密,在一个逻辑步骤内实现了选票的加密及签名,分析得出协议具有正确性、唯一性、隐私性、公正性、可验证性等特性,并对协议的不可伪造性进行了形式化证明。实验结果表明,本文协议的运行时间和gas 消耗较Lyu 协议均有所降低,但随着投票人数的增加,上传至区块链的数据量也有所增加。下一步将引入IPFS 文件系统,使密钥参数、选票、签名等数据存储至IPFS 文件系统,且在区块链上只存储这些数据的指针或索引,以降低上传至区块链的数据量。

