基于加权共享近邻与累加序列的密度峰值算法

王芙银，张德生，肖燕婷

（西安理工大学 理学院，西安 710054）

0 概述

聚类作为一种无监督学习方法，是数据挖掘领域［1］的重要技术之一。聚类的主要目的是依照所定义的聚类准则，将一组杂乱的数据中具有相似特征的数据点划归为一个类簇，同时使得不同类簇之间具有显著差异［2］。在如今万物互联、大数据蓬勃发展的当下，所产生的数据量也正在爆炸式增长，因此，寻求一种高效的数据聚类方法显得尤为重要。近年来，许多学者相继提出了多种不同的聚类算法，按照不同的算法原理可将其分为基于划分的聚类、基于层次的聚类、基于网格的聚类、基于密度的聚类、基于模型的聚类这五大类，这几类不同的聚类算法各自都具有独特的优势并得到了广泛研究与应用。

DBSCAN［3］作为一种典型的基于密度的聚类算法，能够有效识别任意形状的数据，且具有较好的聚类效果，但该算法在聚类过程中易受邻域参数的影响，其结果往往需要反复调参才能确保精确。RODRIGUEZ 等［4］于2014 年提出一种新的基于密度的聚类（DPC）算法，该算法因具有原理简单、高效等优点，自提出以来便引起许多学者的关注，且被广泛应用于图像处理［5］、生物医学［6］、文档处理［7］等领域，但是，DPC 算法也存在一些缺陷，如聚类结果受局部密度及其相对距离的影响、截断距离需要人为设定且参数的选取较为敏感、聚类中心的选取需人为参与决策、算法难以处理密度分布差异较大和复杂的流形结构数据，这些问题提高了算法在聚类过程中的主观性与不稳定性。

为提高DPC 算法的适用性，很多学者都对其做了相应的改进。DU 等［8］提出一种基于KNN 的改进密度峰值聚类（DPC-KNN）算法，将KNN 与主成分分析法引入局部密度的计算过程，充分考虑数据的邻域分布特征，从而更好地识别边界点的类别。PARMAR 等［9］采用残差来测量邻域内的局部密度，提出一种基于残差的密度峰值聚类（REDPC）算法，其能够更好地处理包含各种数据分布模式的数据集。LIU 等［10］指出DPC 算法中如局部密度及最短距离度量方法、剩余点分配策略等所存在的一些问题，提出一种基于共享近邻的聚类方法，该方法通过共享近邻重新定义密度及其距离的计算方式，最后设计两步分配方式对剩余点进行分配，其有效提高了算法的聚类性能。XIE 等［11］提出一种基于模糊加权K 近邻的改进DPC（FKNN-DPC）算法，利用K个最近邻个体之间的距离之和来衡量密度，并用一种新的分配方式对剩余点进行分配。CHENG 等［12］提出一种新的基于自然邻居优化的DPC 算法，该改进算法可以很好地反映数据的分布，且无需任何参数。HOU 等［13］提出仅基于相对密度关系的聚类中心识别准则，以增强密度峰值聚类算法的聚类效果。FLORES 等［14］通过检测一维决策图中数据点之间的间隙来自动确定聚类中心。LIANG 等［15］提出一种基于分治法的改进DPC 算法，该算法在不需要任何先验条件的情况下能够自动寻得聚类中心。QIAO等［16］引入一种新的不对称度量指标，增强了算法查找边界点的能力，解决了DPC 算法在分布不均的数据上聚类效率不高的问题。XU 等［17］提出一种具有密度敏感相似性的密度峰值聚类（RDPC-DSS）算法，其有效提高了流形数据的聚类精度。

本文提出一种基于加权共享近邻与累加序列的密度峰值（DPC-WSNN）算法。定义一种新的基于加权共享近邻的局部密度度量公式，替代DPC 中根据截断距离dc所定义的密度公式，避免因dc选取不当而影响聚类效果，同时，利用加权共享近邻并进一步考虑全局一致性，以有效处理不同类簇数据集分布不均的情况。在选取聚类中心的过程中，在原有决策值γi=ρiδi的基础上，重新定义γ的计算方式，借鉴ZHOU 等［18］在灰色预测模型中所定义的一阶累加序列生成方式，产生一组γ的累加序列，根据所产生的累加序列数值变化情况来实现类簇中心的自动选取，从而避免手动选取聚类中心所带来的误差。

1 密度峰值聚类算法

DPC 算法在实现过程中主要基于以下2 个假设：

1）聚类中心被一群密度较低的点包围。

2）聚类中心与其他高密度点之间的最短距离足够远。

基于上述2 个假设，选取一个合适的截断距离参数dc，用来求解数据点的局部密度ρ及其相对距离δ值，最后根据决策图找出聚类中心并分配剩余点。对于数据集X={x1,x2,…,xn}，dij表示数据点i与点j间的欧氏距离。数据点的局部密度有2 种不同的定义方式：

1）在截断核的定义下，点i的局部密度ρi定义为：

当dij＜dc时，χ(dij-dc)=1；否则，χ(dij-dc)=0。

2）在高斯核的定义下，ρi如式（2）所示：

点i到其他高密度点间的最短距离δi定义为：

当计算出所有点的局部密度ρi以及相对距离δi后，选择ρi与δi均较大的点作为聚类中心，将剩余点分配给与之较近的高密度点所在的类簇中从而完成聚类。

2 DPC 算法改进

2.1 基于加权共享近邻的局部密度改进

DPC 算法定义了2 种密度计算方式，2 种方式都是以欧几里得距离来衡量数据点的密度，但是欧几里得距离只考虑数据点之间的局部一致性特征，忽略了全局一致性特征，因此，当数据样本点分布不均时，基于欧几里得距离得到的密度通常不能准确地捕捉到固有的数据结构，最终导致聚类性能下降。为了适应更多复杂且分布不均的数据集，本文将共享近邻引入密度计算中，充分考虑样本的整体分布，以更好地平衡样本点的全局一致性与局部一致性。共享近邻［10］与样本间的相似度定义如下：

定义1（共享近邻）对于数据集X中的样本点xi与xj，点xi的K 近邻记为Γ(xi)，点xj的K 近邻记为Γ(xj)，则点xi与xj的共享近邻SNN(xi,xj)定义为：

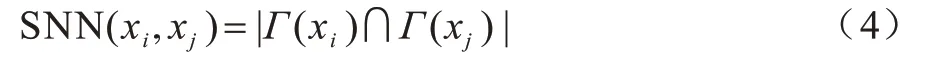
定义2（样本间的相似度）根据共享近邻的定义，样本点xi与xj间的相似度sij定义为：

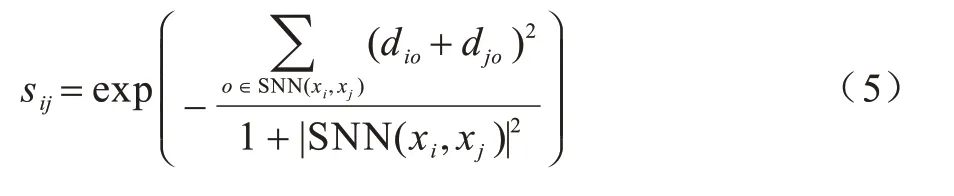
其中：ο为共享近邻中所取的样本点；|SNN(xi,xj)|表示属于共享近邻的样本数目，其值越大，表明点i、j的相似度越大，(diο+djο)越小，点i、j之间的相似度也越大。当2 组样本的共享近邻数目相等时，如图1 所示，点i和j、点i和k的共享近邻个数 都为1，且 此时dij=dik，根据三角形的三边关系可知，有根据式（5）所定义的相似度，则认为点i与点k间的相似度大于点i与点j间的相似度，这样更能反映空间中样本点的分布特征。

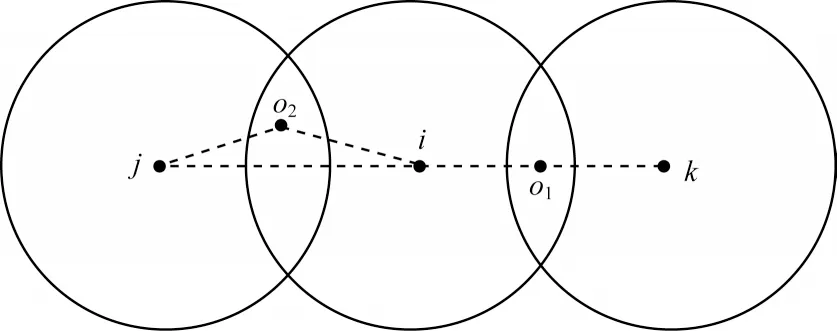
图1 共享邻居示意图Fig.1 Schematic diagram of shared neighbors

此外，在面对不同密度和大小的类簇时，位于数据密集区域的样本点和位于数据稀疏区域的样本点对聚类中心选取的贡献度不一样，因此，在解决数据分布不均的问题上，除对数据进行过采样和欠采样调节外，对样本点的贡献度进行加权处理也可以起到很好的平衡作用。本文以样本点间的共享近邻数作为密度的重要衡量指标，以对每个样本点所在的区域相似度进行权重调整，为此，引入图2 所示的sigmoid 函数，其定义如下：

图2 sigmoid 函数图像Fig.2 Image of the sigmoid function

相比于一元一次函数，sigmoid 函数在一定程度上可以对数据相似度进行权重调整，减少了因数据分布不均而带来的误差。本文将sigmoid 函数引入密度计算中，以互近邻点的数目作为变量x值，分析可知，在式（6）中，当共享近邻数目较多时，表明2 个样本点间的相似度较高，有较大的可能性会被聚为一类，通过图2 函数变化图像可知，当互近邻点的数目足够多时，其函数值为1，这表明在处理高密度区域的点时，所加权重接近1，对于高密度样本点而言，其本身就有较大概率被选作聚类中心，此时可令其相似度的权重为1，当互近邻点的数目不断减少或为0 时，其权重则由1 非线性递减到0.5，这时非聚类中心点与聚类中心有了更加明显的区分，能够使得式（5）所定义的相似度更具合理性和准确性。经过加权后，局部密度ρi如定义3 所示。

定义3（局部密度）对于样本点i，根据其相似度定义密度ρi为：

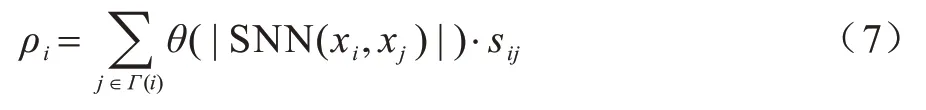
通过定义3 所给出的密度度量公式，可计算出数据集中所有点的局部密度及相对距离。

为了进一步说明所改进的密度在处理分布不均数据集时的有效性，以Pathbased 数据集为例，DPC算法与加权共享近邻的改进DPC 算法的决策图如图3 所示。从图3（a）可以看出，DPC 的决策图在确定聚类中心时很容易将第3 个聚类点处理为噪声点，从而导致最终聚类结果出现偏差；从图3（b）可以看出，对密度进行改进后，决策图中聚类中心分布在右上角，均位于高密度区域，通过该决策图可以准确选出目标聚类中心。实验结果表明，改进DPC 可以对数据进行全局考虑，解决数据集中的分布不均问题，从而确定正确的聚类中心。

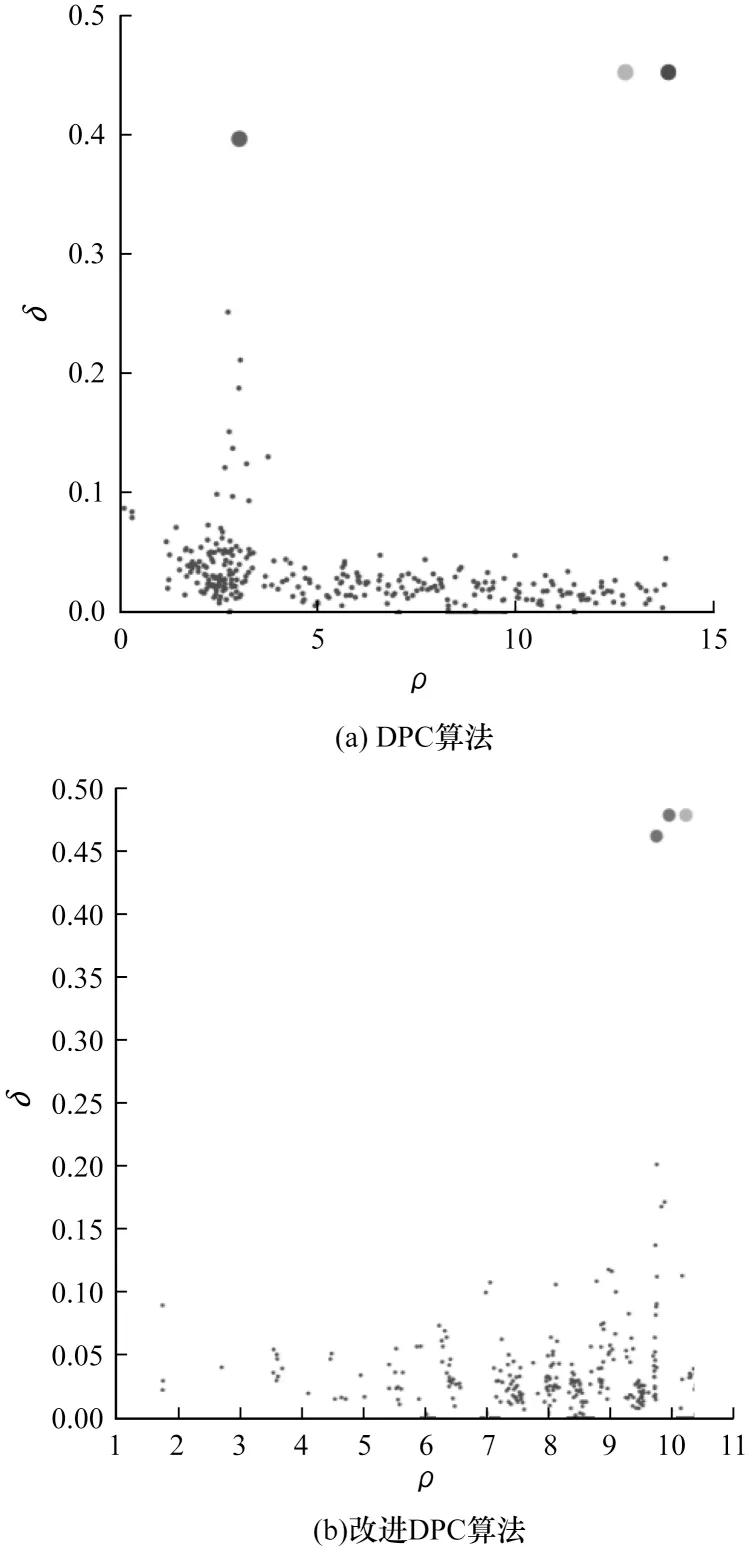
图3 2 种算法的决策图对比Fig.3 Comparison of decision diagrams of two algorithms

2.2 聚类中心选取方法改进

DPC 算法在选取聚类中心时，需要人为参与决策，通过决策图来选取ρ与δ均较大的点，但对于聚类中心较多的数据集，这种方法显得复杂低效，而且出现错选的概率较大。本文提出一种新的聚类中心选取方法，首先定义决策值γi如下：

为消除ρi与δi量纲不同而造成的误差，对ρi与δi进行归一化处理，将归一化后结果的乘积作为决策值γi。本文将γi进行降序排列得到一组降序值，将其记为γ′，根据聚类中心的性质可知，在γ′=[γ1,γ2,…,γn]中，只有前面几个较大值所对应的点应被选作聚类中心。对此，本文参考文献［18］所定义的一种新的非负序列累加生成方法，对于非负序列定义其累加序列为其中：

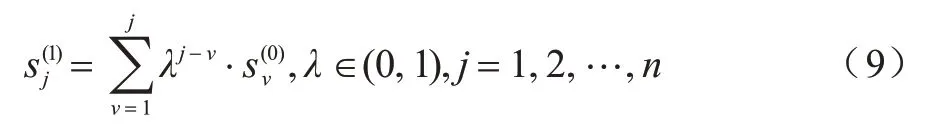
观察式（9）可知，由于λ∈(0,1)，因此该序列在累加过程中，靠前位置信息的影响权重在不断降低，而信息越靠后，权值越大。

对于γ′而言，需要保留前面一部分较大的值，因此，本文对式（9）进行调整，使其在累加过程中不断降低序列靠后位置信息的权值，而增大靠前位置信息的权重，使其更好地满足本文的需求。修改后的累加定义如下：

由于γ′为降序排列的序列，因此在逐步累加的过程中，累加序列的值也越来越接近，最终大量的点会不断地集中在一起。在累加序列γ(t)中，定义均值μ为：

在选取聚类中心时，只需在γ(t)序列中挑选比均值μ小的点，将其作为聚类中心。以类别数为7 的Aggregation 数据集为例，图4 展示了其γ′的累加序列分布情况（彩色效果见《计算机工程》官网HTML版），图4（b）是图4（a）中方框线内的局部放大图，以便更好地观察均值μ的位置分布。从图4（b）可以看出，在累加过程中，大量的点不断地集中在一起，红色点u表示这组序列的均值μ，其也位于堆积点附近，而聚类中心点对应的累加值则位于均值的前方，此时只需选取那些累加值小于均值的点作为中心进行聚类即可，即将前7 个γ′所对应的点选取为聚类中心。因此，将累加序列γ(t)的均值作为聚类中心和非聚类中心的临界点，可以准确选取聚类中心，从而实现聚类中心的自适应。

图4 Aggregation 数据集的γ(t)序列分布Fig.4 γ(t)sequence distribution of Aggregation dataset

综上，聚类中心选取策略步骤为：

1）根据式（8）和式（11）得到累加序列γ(t)，并求得其均值μ，将小于均值μ的γ′个数作为聚类中心数目m。

2）将前m个γ′值所对应的点选取为聚类中心。

2.3 算法描述

改进DPC 算法描述如算法1 所示：首先，计算样本点间的距离矩阵；然后，根据式（3）、式（7）分别计算相对距离与局部密度，在求得每个点的距离与密度后，根据式（11）、式（12）自动选择聚类中心；最后，按照DPC 的分配策略对剩余点进行分配聚类。

算法1DPC-WSNN 算法

2.4 算法复杂度分析

对于含有N个样本点的数据集，DPC 算法的时间复杂度为O(N2)。对于本文所提的DPC-WSNN 算法，设近邻数为K，其计算局部密度ρi是基于共享近邻的，时间复杂度为O(KN)；在选取聚类中心时，需多计算一个决策值γi，其时间复杂度为O(N)。综上，本文所提DPC-WSNN 算法的时间复杂度为（O(N2)+O(KN)+O(N))～O(N2)。因此，相较于DPC 算法，DPC-WSNN算法的时间复杂度并未增加。此外，在相关算法中，FKNN-DPC 算法的时间复杂度为O(N2)，DBSCAN 算法的时间复杂度为O(N2)，AP 算法与K-Means 算法的时间复杂度分别为O(N2lbN)与O(N)。

3 实验结果及分析

3.1 实验数据集

为了评估本文所提算法的有效性，采用如表1、表2 所示的8 个合成数据集和8 个UCI 数据集对其进行验证。

表1 合成数据集Table 1 Synthetic datasets

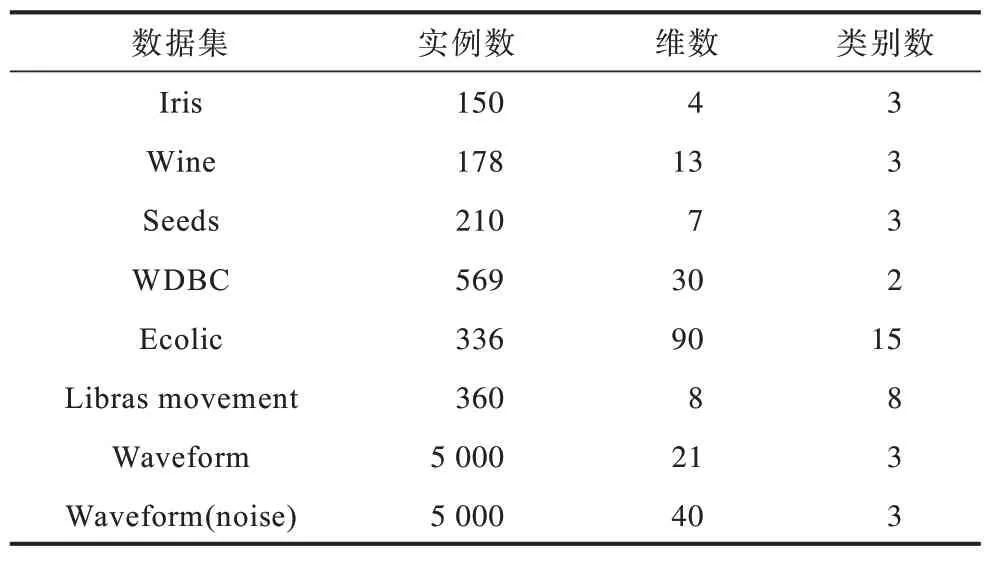
表2 UCI 数据集Table 2 UCI datasets

3.2 评价指标

在实验中，本文将DPC-WSNN 算法的聚类结果与FKNN-DPC、DPC、DBSCAN、AP、K-Means 的聚类结果进行比较，评价指标选取FM 指数（FMI）［19］、调整兰德指数（Adjusted Rand Index，ARI）［20］和调整互信息（Adjusted Mutual Information，AMI）［21］。各指标具体如下：

1）FMI 指标。FMI 是成对精度与召回率的几何均值，定义如下：

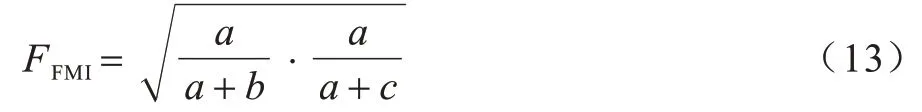
其中：a表示在C和C*中都属于同一类的数据点对数；b表示在C中属于同一类但在C*中不属于同一类的数据点对数；c表示在C*中属于不同类但在C中属于同一类的数据点对数。FMI 指标的取值范围是[0,1]，数值越大表示聚类效果越好。

2）ARI 指标。兰德指数（RI）的定义式为：

其中：a代表在C和C*中都属于同一类的数据点对数；b代表在C*中属于不同类但在C中属于同一类的数据点对数代表数据集中可组成总元素的对数。在使用RI 指标时，不能保证类别标签在随机分配的情况下其值接近0。因此，本文引入ARI［20］来解决这一问题，ARI 指标的定义式为：

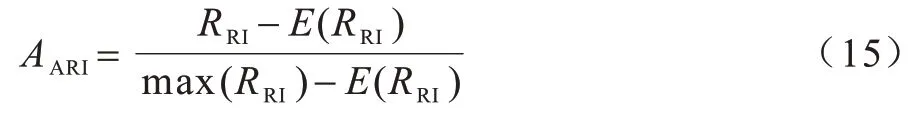
其中：E(RRI)表示RI 的数学期望。ARI 的取值范围为[-1,1]，值越大表示聚类结果越精确。

3）AMI 指标。与ARI 相似，AMI 也是一种常见的聚类评价指标，其定义式为：

其中：H(A)、H(B)表示2 个类别标签的熵。AMI 是基于互信息（MI）来衡量聚类效果的类别信息，E(MMI)表示MI 的数学期望。AMI 的取值范围是[-1,1]，值越接近1 表示聚类结果越好，即与真实结果越吻合。

3.3 算法参数设置

为了更好地测试算法的聚类效果，对各对比算法进行参数调优。DPC-WSNN 算法和FKNN-DPC算法需要设定样本近邻数K，该参数可根据不同数据集在5～30 之间择优选取。DBSCAN 算法需要设定邻域半径ε和邻域内包含的最少样本数Minpts，其中，邻域半径ε以0.01 为步长，在0.01～1 之间选取，邻域内包含的最少样本数Minpts 在5～30 之间选取。AP 算法没有通用的规则来选取参数，本文考虑将参数搜索上限设置为最大相似度的几倍，逐渐缩小搜索范围［10］。由于K-Means 算法中类簇中心的选取对聚类结果有较大影响，因此对每个数据集进行30 次重复实验，取最优结果。

3.4 结果分析

选取8 种合成数据集和8 种UCI数据集，对本文所提算法进行测试和评价，并将其实验结果与FKNN-DPC、DPC、DBSCAN、AP、K-Means 进行对比，各算法的3 种评价指标值如表3～表6 所示，其中，加粗值表示最好的聚类结果。从表3、表4可以看出，本文所提DPC-WSNN算法相比其他对比算法具有更好的聚类表现，尤其对于Jain 数据集，本文算法的聚类准确率较对比算法具有大幅提升。从表5、表6 可以看出：对于维度高且样本点密度变化大的数据集，DPC、DBSCAN、AP、K-Means的聚类效果都不理想，无法得到较高的聚类指标值；FKNN-DPC 算法在Wine 数据集上达到最优，而在其他数据集上的聚类效果略差于DPC-WSNN 算法，由于DPC-WSNN 算法在DPC 的基础上引入SNN 来对密度公式进行改进，充分考虑了数据分布稀疏的情况，进而可以得到更准确的密度。DPC-WSNN 在UCI 数据集上的聚类指标值整体更高，在所有对比算法中，其聚类表现最优，在其他数据集上也能达到较好的聚类效果。相比DPC 算法和其他几种对比算法，DPC-WSNN 算法在处理大部分问题上均能达到较好的效果。

表3 6 种算法在前4 个合成数据集上的聚类结果比较Table 3 Comparison of clustering results of six algorithms on first four synthetic datasets

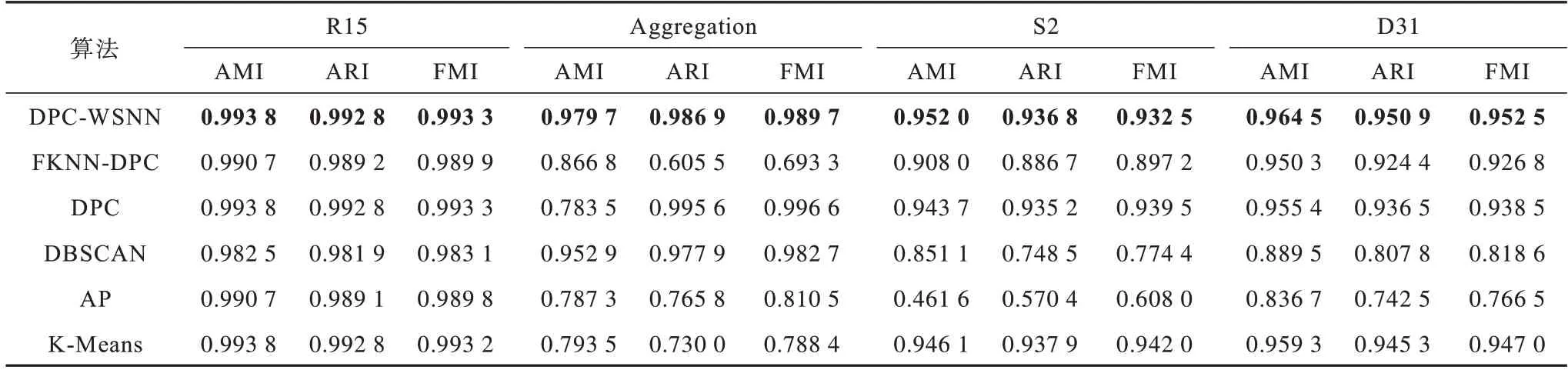
表4 6 种算法在后4 个合成数据集上的聚类结果比较Table 4 Comparison of clustering results of six algorithms on last four synthetic datasets

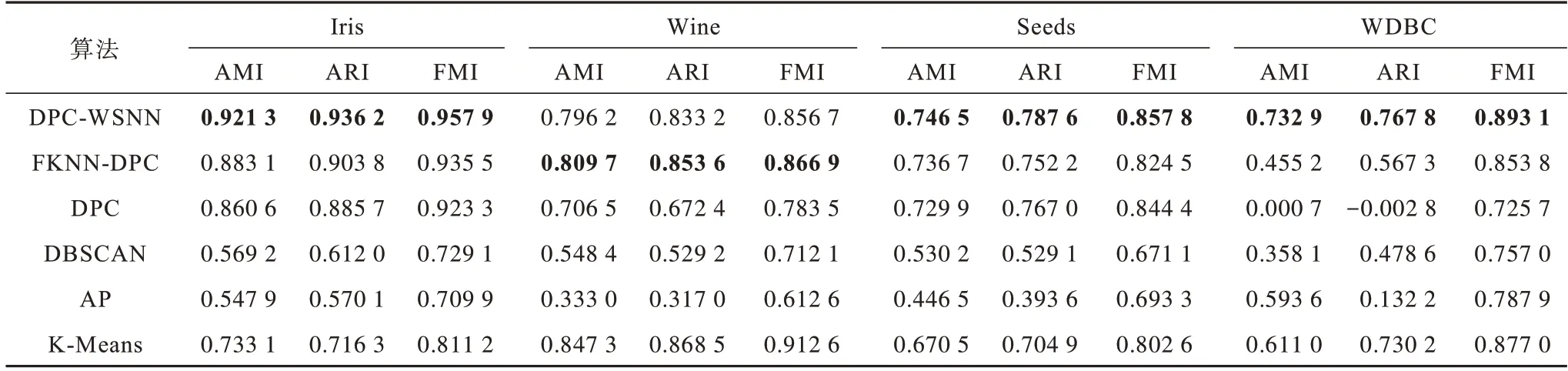
表5 6 种算法在前4 个UCI 数据集上的聚类结果比较Table 5 Comparison of clustering results of six algorithms on first four UCI datasets

图5～图7分别为DPC-WSNN、FKNN-DPC、DPC、DBSCAN、AP、K-Means 这6 种对比算法在Jain 数据集、Flame 数据集、Pathbased 数据集上的聚类效果（彩色效果见《计算机工程》官网HTML 版），图中不同颜色的点被分配到不同的类簇中，其中，蓝色星形代表聚类中心点，叉形代表噪声点。

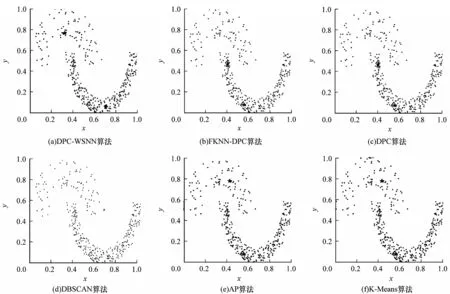
图5 6 种算法在Jain 数据集上的聚类效果Fig.5 Clustering effects of six algorithms on Jain dataset

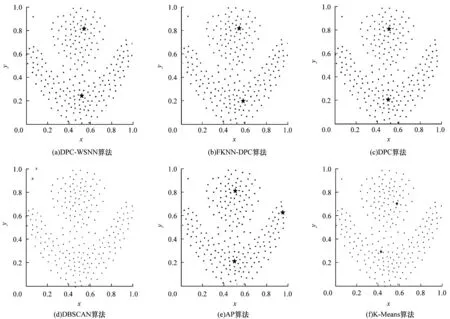
图6 6 种算法在Flame 数据集上的聚类效果Fig.6 Clustering effect of six algorithms on Flame dataset

图7 6 种算法在Pathbased 数据集上的聚类效果Fig.7 Clustering effects of six algorithms on Pathbased dataset

从图5 可以看出：本文DPC-WSNN 算法不仅可以找到正确的聚类中心，而且聚类结果也完全正确；DPC-KNN 算法、DPC 算法、AP 算法、K-Means 算法都将本该属于下半部分的类簇错误地分配到了上半部分，从而出现了错误的聚类结果；DBSCAN 算法下半部分类簇的聚类结果正确，但上半部分左端几个数据点被错误分配。

从图6 可以看出：DPC-WSNN 算法、DPC-KNN算法、DPC 算法、DBSCAN 算法均得到了正确的类簇数目，其中，DBSCAN 算法将左上角的2 个点识别为噪声点，导致聚类准确率有所降低，AP 算法错误地识别类簇数目，导致将聚类结果分为了3 类，而K-Means 算法将本该属于红色类簇的点错误地分配给了蓝色类簇。

从图7 可以看出：本文DPC-WSNN 算法聚类准确度较高；AP 算法不能准确识别出类簇中心，导致聚类结果出现明显偏差；DPC-KNN 算法、DPC 算法和K-Means 算法虽能正确识别类簇中心，但将半环部分的类簇点进行了错误分配；在DBSCAN 算法中，虽然2 个类簇被正确分配，但半环部分被识别为噪声点，导致聚类准确率大幅降低。

3.5 参数敏感性分析

DPC-WSNN 算法在运行过程中，需要人为设置参数K值，为了验证该参数对算法聚类结果的影响，通过改变参数K值大小来探索DPC-WSNN 算法在不同数据集上的聚类结果变化。实验选取3 个合成数据集和3 个UCI 数据集，以AMI 值作为稳定性衡量指标，K在5～30之间取值，所得的AMI指标值结果如图8所示。从图8 可以看出：对于合成数据集而言，不同的K值所得到的结果较为稳定，波动较小，具有很好的鲁棒性；对于UCI 数据集，前期当K取值较小时，聚类值有一定的波动，但随着K的不断增大，其波动逐渐减小，结果趋于稳定，这意味着当K近邻个数增大时，所设计的加权共享近邻的密度度量具有更好的优势，因此，聚类实验验证了DPC-WSNN 算法对参数K的敏感性较低，算法具有较强的鲁棒性。

图8 K 值对DPC-WSNN 算法聚类效果的影响Fig.8 Influence of K values on clustering effect of DPC-WSNN algorithm

4 结束语

本文对DPC 算法进行改进，提出一种基于加权共享近邻与累加序列的密度峰值算法DPCWSNN。该算法考虑各数据点的邻域分布情况，利用加权共享近邻重新定义局部密度的度量方式，同时使用γ的累加序列来实现聚类中心的自动选取。实验结果表明，相比DPC、AP 等算法，DPC-WSNN算法具有较高的聚类准确度。本文算法执行过程中涉及参数K，虽然参数K相较截断距离dc更容易确定，但其仍然需要人为决策。此外，DPC 算法对剩余点的分配方法也可能会影响DPC-WSNN 的聚类效果。因此，实现参数K的自适应以及对DPC 算法中剩余点分配策略进行改进，将是下一步的研究方向。