考虑特征重要性值波动的MI-BILSTM 短期负荷预测

孙 辉，杨 帆，高正男，胡姝博，，王钟辉，刘劲松

（1. 大连理工大学电子信息与电气工程学部,辽宁省 大连市 116024；2. 国网辽宁省电力有限公司电力科学研究院,辽宁省 沈阳市 110055；3. 国网辽宁省电力有限公司调度控制中心,辽宁省 沈阳市 110004）

0 引言

短期负荷预测通过对数学、统计学等各种分析工具的运用,探究历史负荷之间的关系与规律,并对未来几小时或几天的负荷大小进行推测［1］,以保障电力系统的安全运行。近年来,随着储能、新能源、电动汽车接入电网的规模不断增大,以及基于激励、价格的需求侧响应模式的持续发展,短期负荷预测的复杂度明显增加。同时,在电力市场化改革不断推进的背景下,高效、实时的电力交易成为必需,这给短期负荷预测的精确性、快速性和可靠性提出了更高的要求。

围绕着电力负荷数据强时序性和强非线性的特点,国内外学者持续不断地开展研究。目前,基于机器学习的短期负荷预测已经成为相关领域研究和应用的热点之一。文献［2-4］使用支持向量机进行负荷预测,文献［5-7］采用了人工神经网络方法。上述方法能够很好地解决非线性问题。但是,以上方法的共同缺点在于对负荷的时序信息考虑不够,需要手动添加相关信息。近年来,深度递归网络（RNN）、长短期记忆（LSTM）网络（下文简称LSTM）和门控循环单元（GRU）等凭借其特有的循环单元,能够同时处理时序性和非线性问题,使得深度学习模型在短期负荷预测中被广泛应用。文献［8-9］基于LSTM 进行短期负荷预测,提高了预测精度；文献［10-12］以GRU 为底层模型进行负荷预测,验证了其有效性；文献［13］将孪生网络、灰狼优化算法和LSTM 结合进行负荷预测,在保证预测值精度的同时,提高了算法的运行效率；文献［14-15］采用双向长短期记忆（BILSTM）网络（下文简称BILSTM）进行负荷预测,证明了相较于LSTM,BILSTM 对于连续时间序列具有更好的表达能力。为了防止参数过多影响训练效率［16］,文献［8-15］中的模型采用权值共享结构对电力负荷的时序信息进行提取,文献［17］首次对权值共享结构的时不变性进行讨论,但目前的研究中尚未针对时不变性对负荷预测的影响进行探究。

在使用深度学习模型进行短期负荷预测前,需要选取影响负荷变化的因素作为输入特征,包括气象、日期和历史负荷值等。输入特征在不同时刻下对负荷变化的影响力不同,即其重要性值发生了波动。例如,温度在一天中的不同时刻对负荷变化的影响大小具有明显差异［18］。而权值共享结构的时不变性,使之不能动态追踪输入特征的重要性值随时间而产生的波动,进而影响预测精度。因此,需要量度不同时刻下输入特征的重要性,并进行动态修正,以提高预测精度。文献［19-20］采用皮尔逊相关系数（PCC）法量度输入特征的重要性,但PCC 只能反映线性相关性。 近年来,互信息（mutual information,MI）法由于其非线性提取能力和自适应性在量度特征重要性中被广泛应用［21-23］。但上述量度特征重要性的研究是进行输入特征选择,未能将所选择的输入特征重要性值随时间而发生的波动考虑在内,无法补足权值共享结构的缺陷。

为了追踪输入特征的重要性值随时间出现的波动,进一步提高预测精度,本文提出一种考虑特征重要性值波动的MI 和BILSTM（下文简称MIBILSTM）短期负荷预测方法。该方法先采用MI 法提取不同时刻下输入特征的重要性值,形成重要性值波动矩阵。接着,通过矩阵对原始输入特征进行动态修正,使之内部包含波动信息。最后,将修正后的输入特征代入BILSTM 中进行短期负荷预测,不仅保留了权值共享结构在精简参数方面的优势,并且弥补了其无法提取重要性值波动的缺陷,提高了预测精度。

1 权值共享结构分析及重要性值波动矩阵提取

1.1 权值共享结构分析

LSTM 预测结构见图1。采用LSTM 预测时,对应某一时刻t的输出预测值ot,有z种不同种类的输入特征序列it=[it,1,it,2,…,it,z]T,不同时刻的输入序列保持相同的种类和结构,输入特征序列所对应的权值W=[w1,w2,…,wz]。例如,第1 类特征it,1对应的权值为w1,第2 类特征it,2对应的权值为w2,以此类推。特征所对应的权值越大,说明该特征对于最终的输出负荷影响越大,即特征的重要性越大。但是由于LSTM 权值共享机制的时不变性,在不同时刻的输入序列所对应的权值W=[w1,w2,…,wz]保持不变,即认为不同时刻下输入特征具有同样的重要性,换而言之,权值共享机制不能随时间动态追踪输入特征的重要性值波动,这会导致最终的预测精度下降。因此,事先提取出输入特征的重要性值波动信息,再代入模型中进行预测,就可以弥补权值共享结构的不足,具体理论推导过程如附录A 所示。其他含有权值共享结构的深度学习模型分析与LSTM 类似,不再赘述。

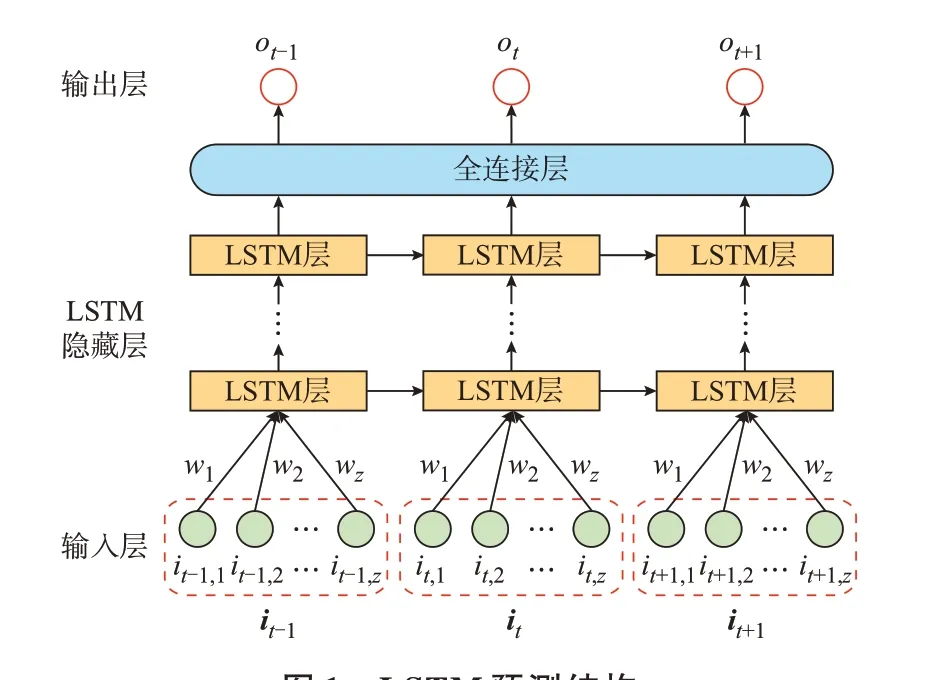
图1 LSTM 预测结构Fig.1 Structure of LSTM forecasting

1.2 重要性值波动矩阵

采用MI 法量度输入特征的重要性,用提取到的MI 值表征输入特征的重要性值,MI 值越大,说明输入特征与负荷之间的相关性越大,即重要性值越大。按照一天中采样点的先后顺序,依次提取输入特征的重要性值,以时间维度为行,输入特征种类为列,形成重要性值波动矩阵。通过矩阵中具体数值的大小,反映输入特征重要性值的时序波动。

此外,日负荷场景受多种因素（日期特征、温度、湿度等）影响,可以分为不同类型,其输入特征的重要程度大小也表现出明显的差异。例如,高温场景下由于空调、电风扇、冷气机等降温设备的使用,温度的重要程度会明显增大。因此,重要性值波动矩阵的提取分为两步:首先,采用高斯混合模型（Gaussian mixture model,GMM）聚类从原始数据库中划分出不同的日负荷场景；其次,针对划分出的具体场景,分别提取输入特征的重要性值波动矩阵。

1.2.1 基于GMM 的日负荷场景聚类

GMM 聚类按照概率划分成员,具有更加灵活的类簇形状。GMM 聚类后生成的结果为一系列的概率值,样本中的个体对应不同的类别都有其对应的概率,选取最大概率的所属类别作为分类依据。采用期望最大化（expectation-maximization,EM）算法估计GMM 中单个高斯分布函数参数。EM 算法分成期望步和最大化步。

1）期望步:根据给定的初始值或前一步最大化步计算得出的3 组参数,计算样本xi由第j类别所生成的概率γj(xi),3 组参数如式（1）所示,计算公式见式（2）。

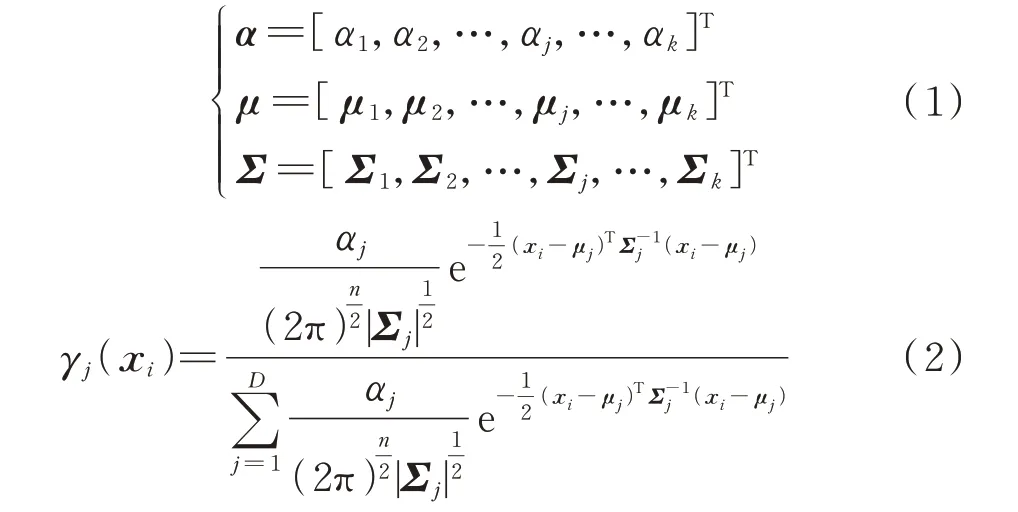
式中:αj、μj和Σj分别为第j个高斯分布的权重、均值和协方差；k为高斯分布的总个数；xi为日负荷场景划分的输入数据；n为xi的维度；D为日负荷数据库中的总天数。

2）最大化步:根据最大似然估计对上述3 组参数α、μ和Σ进行更新,如式（3）所示。

式中:α′j、μ′j和Σ′j分别为第j个高斯分布更新后的权重、均值和协方差。

循环进行上述期望步和最大化步,直至参数收敛或似然函数收敛,得到日负荷场景聚类结果。GMM 聚类的超参数（最佳聚类数量）常采用贝叶斯信息准则（Bayesian information criterion,BIC）确定［24］,选取最低BIC 值所对应的聚类数量作为最优值。BIC 值的计算公式和原理见附录B。

关于选取表征日负荷场景划分的输入数据如下:

日期特征是影响日负荷场景划分的显著因素。因此,初次GMM 聚类以日期特征为输入完成聚类。日期特征分为工作日、周末、法定节假日3 种不同的情况,按照one-hot 编码形式对日期特征进行编码,即工作日为［1,0,0］,周末为［0,1,0］,法定节假日为［0,0,1］。当周末与法定节假日重合时,统一按照节假日处理,后续在节假日场景下进行预测时,加入“是否为周末”这一特征作为区分。将上述经过编码后的三维日期特征作为初次GMM 聚类的输入,完成初次聚类,得到以日期特征为划分的日负荷场景。

二次GMM 聚类以气象特征作为输入,对日负荷场景进一步细分。气象特征包括温度、湿度、降水量等不同类型的数据。由于温度是影响日负荷变化的显著因素,选用一天中的最高温度、最低温度、平均温度作为二次GMM 聚类的输入,得到最终的日负荷场景划分结果。

1.2.2 基于MI 提取重要性值波动矩阵

MI 来自信息论中熵的概念,反映任意两个随机变量之间的相关性关系。用输入特征和负荷之间的MI 值表征输入特征的重要性值。

MI 值的计算公式为:式中:M(P,Q)为随机变量P和Q之间的MI 值；pPQ(p,q)为随机变量P和Q的联合概率密度函数,其中,p和q分别为P和Q中的元素；pP(p)为随机变量P的边缘概率密度函数；pQ(q)为随机变量Q的边缘概率密度函数。两个变量间的相关性越强,MI值越大,当两个变量相互独立时,MI 值为0。

重要性值波动矩阵的具体提取步骤如下:

步骤1:确定输出负荷数据集。根据上述日负荷场景划分结果,将电力负荷数据集按照一天中的负荷采样点个数分成n组,并将其作为输出数据集O=[O1,O2,…,Ot,…,On],其中,Ot为t时刻的输出负荷数据。

步骤2:确定输入特征数据集。取与上述输出负荷数据集相对应的输入特征矩阵I,即

其中,t时刻输出Ot对应的输入特征It=[It,1,It,2,…,It,z]T。

步骤3:t时刻输入特征的重要性值计算。计算t时刻输入特征与输出负荷的MI 值并进行归一化处理得Mt=[M(It,1,Ot),M(It,2,Ot),…,M(It,z,Ot)]T,用上述序列中值大小作为t时刻不同输入特征的重要性值,如第1 类输入特征在t时刻的重要性值为M(It,1,Ot)。

步骤4:重复计算步骤3。t从1 到n循环求解不同时刻下输入特征的重要性值,当t=n时,求解完毕。得到随时间变化的输入特征的重要性值波动矩阵M,即

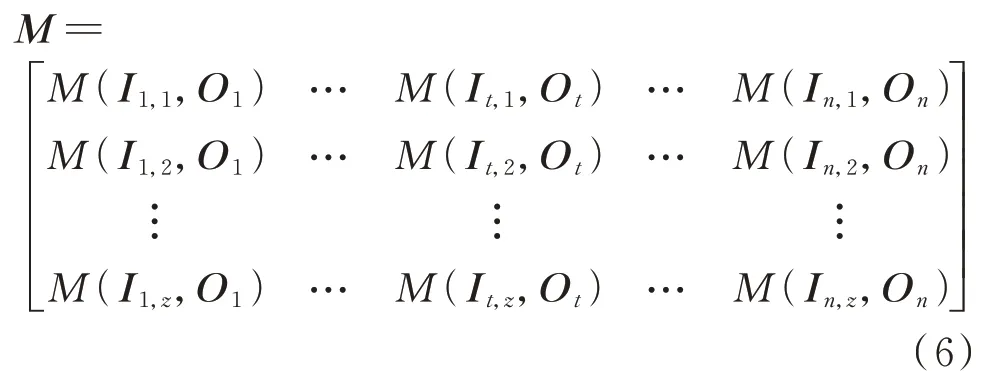
M中包含了不同维度下输入特征的重要性信息。通过横向时间维度对比可以反映同类输入特征在不同时刻下的重要性值波动,而纵向种类维度对比可以反映不同类型的输入特征在同一时刻下的重要性差异。提取重要性值波动矩阵的整体流程如附录C 图C1 所示。

2 基于MI-BILSTM 的短期负荷预测方法

2.1 BILSTM 模型

短期负荷预测中,当前时刻的负荷值同时与历史时刻的信息及未来时刻的信息相关联。本文选用考虑双向时刻信息的BILSTM 作为短期负荷预测的底层模型。基本LSTM 单元的结构如附录A 图A1 所示,BILSTM 结构如附录D 图D1 所示。

BILSTM 的计算公式如式（7）—式（9）所示。

2.2 MI-BILSTM 预测流程

基于MI-BILSTM 的短期负荷预测方法流程见图2。

图2 MI-BILSTM 预测流程图Fig.2 Flow chart of MI-BILSTM forecasting

为了弥补BILSTM 模型权值共享结构的时不变性,将1.2 节提取到的重要性值波动矩阵M作为系数修正BILSTM 的输入特征,如式（10）所示。式中:“°”表示两个矩阵的哈达马积,即两矩阵对应位置的元素分别相乘；I′为更新后的输入特征矩阵。

原输入特征矩阵I经式（10）转换为能反映重要性值波动的输入特征矩阵I′。将I′代入BILSTM 模型中进行训练,使得BILSTM 模型可以动态追踪输入特征的重要程度变化。

3 算例分析

3.1 数据预处理和BILSTM 输入特征选取

选取中国某地区2012 年1 月1 日—2014 年6 月30 日的电力负荷数据库和气象数据库进行算例验证,电力负荷数据采集的时间间隔为15 min,一天采样96 个点,气象数据库为每天的平均温度、最高温度、最低温度、相对湿度和降水量。采用式（11）对数据x进行归一化处理,将数据映射到［0,1］区间上。

式中:x′为归一化后的数据；xmin和xmax分别为数据中的最小值和最大值。

针对聚类后划分的不同数据库,建立相应的MI-BILSTM 模型,模型的输入特征数据分为气象特征、日期特征和历史负荷特征。在所有的日负荷场景下,气象特征保持一致,包括最高温度、最低温度、平均温度、相对湿度和降水量。

对日期特征而言,GMM 聚类已经将不同日期特征下的日负荷场景划分,所以日期特征中不需要区分工作日、周末、法定节假日的特征。但是当两种日期类型重叠或相邻时,负荷曲线会出现相互影响的情况。对于工作日而言,临近休息日（周末、法定节假日）时,负荷曲线会发生变化,例如后一天是休息日时,当天的负荷曲线在后半段会出现跌落；反之前一天是休息日时,当天负荷曲线在前半段会明显较低,所以在工作日场景中加入“是否为休息日前一天”和“是否为休息日后一天”两个特征。如果休息日为周末,该特征取1；如果休息日为法定节假日,该特征取2；如果休息日是周末和法定节假日重叠,该特征取3；不是上述情况取0。对周末而言,主要是受法定节假日导致的调休影响,所以在周末场景下加入“是否为调休日”这一特征,如果该天调休,该特征取1,否则取0。由于初次聚类时,将法定节假日和周末的重叠情况统一按照法定节假日处理,为了表示区分,在法定节假日场景下加入“是否为周末”这一特征,如果是周末取1,否则取0。

历史负荷特征的选取受短期负荷预测的类型影响,由于本文进行的短期负荷预测类型为日前预测,预测日当天的负荷值默认为未知状态,所以选取的历史负荷特征只能从预测日之前的数据库中选取。对工作日而言,选取同一场景下前一工作日对应时刻的负荷值作为历史负荷特征。在周末场景下,选取同一场景下前一相同星期日期对应时刻的负荷值作为历史负荷特征。不同的法定节假日下负荷曲线性质不同,所以选取前一相同节假日对应时刻的负荷值作为历史负荷特征。最终,各日负荷场景下的输入特征种类见附录E 表E1。

3.2 重要性值波动矩阵的提取与分析

3.2.1 日负荷场景聚类结果

根据日期特征和气象特征,分别进行初次GMM 聚类和二次GMM 聚类。其中,GMM 聚类的超参数（最佳聚类数量）采用BIC 确定［24］。按照日负荷场景数目S（S=2,3,…,10）,循环计算对应的BIC 值,将BIC 值最小时对应的日负荷场景数作为GMM 聚类的超参数。

初次GMM 聚类的BIC 值随S逐次增大时发生的变化如附录F 图F1（a）所示。按照BIC,其BIC 值在S=3 时达到最小值,所以选择3 作为最佳聚类数。经初次聚类后从原始数据库中划分出3 类不同的日负荷场景,分别为576 d 的普通工作日场景、228 d 的周末场景和108 d 的法定节假日场景。

温度是影响负荷变化的显著特征,因此,二次GMM 聚类的输入特征为三维温度特征:最高温度、最低温度、平均温度。如附录F 图F1（b）、（c）、（d）所示,工作日场景划分为3 类,分别为工作日1（高温）、工作日2（中温）、工作日3（低温）；周末划分为2类,分别为周末1（高温）、周末2（低温）；法定节假日同样划分为2 类,分别为节假日1（高温）、节假日2（低温）。经过2 次GMM 聚类后,划分出的日负荷场景及其天数如表1 所示。

表1 日负荷场景的聚类结果Table 1 Clustering results of daily load scenarios

3.2.2 重要性值波动矩阵的提取结果

使用MI 法分别提取上述日负荷场景下的输入特征重要性值波动矩阵。数据库中一天的采样点个数为96,按照附录E 表E1 选取输入特征,提取结果如图3 所示。图3 中,为方便表示,用A、B、C、D、E、F、G、H、I、J、K、L 分别表示最高温度、最低温度、平均温度、相对湿度、降水量、是否为休息日后一天、是否为休息日前一天、前一工作日对应时刻负荷值、是否为调休日、前一相同星期日期对应时刻负荷值、是否为周末、前一相同节假日对应时刻负荷值这12 种输入特征。

由图3 可以看出,在不同的日负荷场景下,输入特征的重要性值波动矩阵表现明显不同,验证了提前进行日负荷场景划分的必要性。

图3 输入特征的重要性值波动矩阵展示图Fig.3 Illustration of fluctuant matrix for importance value of input feature

从时间维度上看,由于温度往往通过影响人的行为来影响负荷的变化,所以温度在中高温度的场景下（工作日1、工作日2、周末1、节假日1）所表现出的重要性值往往随着人一天中的生产活动规律发生波动。在一天的凌晨至上午,重要性值逐渐下降,随着生产活动的开启,重要性值逐渐增大至高峰,等到一天的下班时间,重要性值陡然下降,接着晚上用电负荷迎来高峰,温度的重要性值也随之升高。值得注意的是,由于负荷曲线具有在时序上连续的特点,“是否为休息日后一天”在一天中的前几个时刻重要性值较大,而“是否为休息日前一天”在一天中的后几个时刻重要性值较大。历史负荷特征的重要性值在一天中的所有时刻下几乎都保持最大。除了上述有明显规律的特征外,其他特征的重要性值在时序上也同样表现出波动特性。

作为对比,选择经典的PCC 法提取重要性值波动矩阵,提取结果见附录G 图G1。由图可知,在工作日2（中温）、工作日3（低温）场景下,PCC 法提取出的重要性值波动矩阵几乎一致,但中温场景下温度对负荷变化的影响大小应该介于高温场景和低温场景之间,这说明PCC 法应用在中温场景下具有一定的局限性；同样在节假日1（高温场景）的场景下,PCC 法的提取效果也不理想,没有正确反映出高温下温度对负荷变化的影响。而MI 法相较于PCC法,在工作日2、节假日1 下,提取到了更多的非线性关系,这说明MI 法在提取特征的重要性值波动矩阵上有更好的适用性。

3.3 预测结果对比分析

本文选取的算例评价指标为平均绝对百分比误差（MAPE）和均方根误差（RMSE）。经过3.2.1 节的日负荷场景聚类,将原始数据库聚类成7 类不同的日负荷场景,每一类数据库数量按照9∶1 划分出训练集和预测集,进行连续日前预测,训练集和测试集的具体划分结果如附录H 表H1 所示。将3.2.2 节MI 法提取到的输入特征重要性值波动矩阵作为系数按照式（10）对原始输入特征进行修正,修正后代入模型中完成训练和预测。

选 取 LSTM、BILSTM、MI-LSTM、PCCBILSTM、MI-BILSTM 这5 种不同的模型进行对比。由于本文的主要工作在于提取重要性值波动矩阵,并对原始的输入特征进行修正,所以文中在对比时应该控制深度神经网络模型的相关参数不变,观察原始输入特征和修正完成后的特征代入模型进行预测的精度变化。因此,LSTM 和MI-LSTM 模型的参数设置一致,BILSTM、PCC-BILSTM、MIBILSTM 模型的参数设置一致。 LSTM 和BILSTM 模型的超参数采用控制变量法［12,14］多次试验进行模型调优。记录下不同日负荷场景下的MAPE 和RMSE。实验结果见表2。

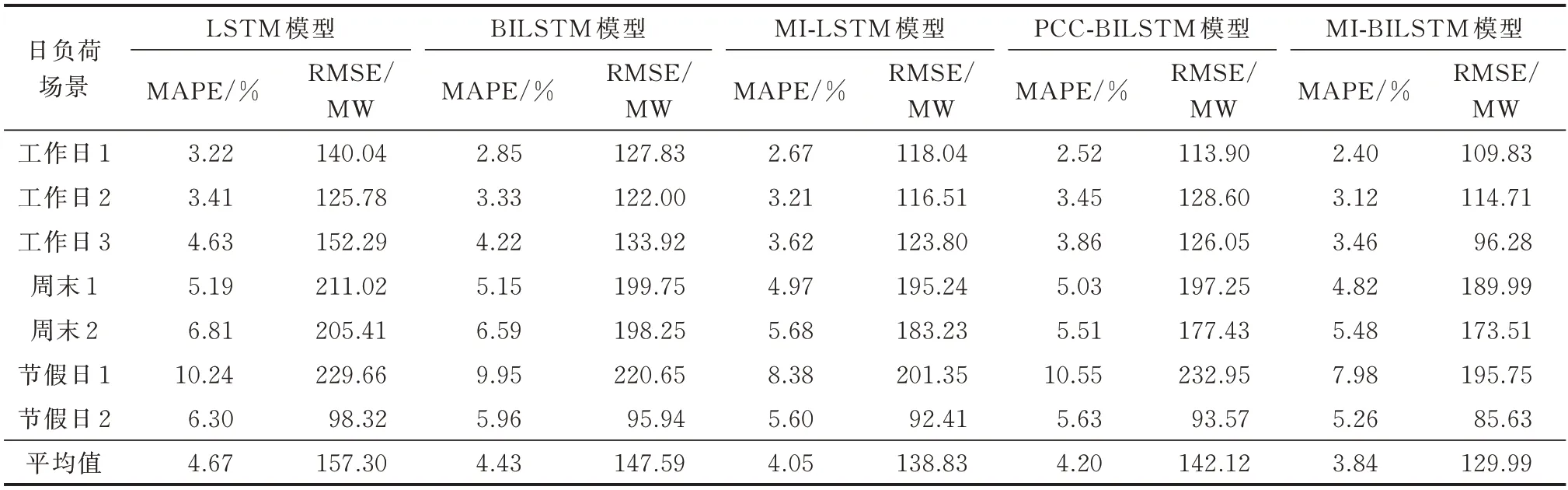
表2 全场景下不同模型预测结果比较Table 2 Comparison of prediction results for different models in whole scenarios

由表2 可知,LSTM 模型的平均预测精度在5 种模型中最低；BILSTM 模型由于可以考虑双向信息,预测精度高于LSTM 模型；MI-LSTM 模型将输入特征的重要性值波动考虑在内,预测精度相较于LSTM 模型有了明显的提高；PCC-BILSTM 模型在多个场景上的精度以及平均精度都优于原BILSTM 模型,这表明采用PCC 法提取重要性波动矩阵也具有一定的适用性。但在工作日2、节假日1场景下,预测精度反而有所下降,这是由于PCC 法线性提取的局限性,导致在工作日2 和节假日1 场景上提取到的波动矩阵未能反映正确的重要性值波动的特性,并因此导致精度下降；对于MI-BILSTM模型,其在7 种不同的日负荷场景下的预测精度都优于其他模型,这说明MI 法提取到的重要性值波动矩阵相较于PCC 法对精度有更明显的提升效果。

MI-BILSTM 模型在工作日1 至3 场景下的MAPE 分别为2.40%、3.12%、3.46%；在周末1 和2场景下的MAPE 分别4.82%、5.48%；在节假日1 和2场景下的MAPE 分别为7.98%、5.26%；在所有日负荷场景下的平均值为3.84%,相较于其他4 种模型的平均值分别提高了0.83%、0.59%、0.20%、0.36%。各场景下MI-BILSTM 模型的RMSE 依次为109.83、114.71、96.28、189.99、173.51、195.75、85.63 MW,平均值为129.99 MW,相较于其他4 种模型的平均值分别提高了27.31、17.6、8.84、12.13 MW。

不同模型结果对比如图4 所示,由图4 可知,MI-BILSTM 模型的预测精度在5 种模型中最高。在负荷曲线的波峰与波谷处,该模型不仅考虑了双向信息流,还实现了输入特征重要性值波动的动态追踪,针对真实负荷曲线具有更好的拟合效果。

图4 不同模型结果对比Fig.4 Result comparison of different models

为了探究重要性值的波动大小与精度提升之间的关系,设计了相关的对比实验,具体如附录I 所示。由附录I 可知,无论是不同场景下还是同一场景下,单纯考虑重要性值波动的大小与预测精度的提升之间均没有明显的正相关或负相关关系,这是因为特征的重要性值波动对精度的影响是一个综合性的影响,不仅每个特征的波动对精度提升具有差异性,而且共同作用时还需要考虑叠加效应。其次,是否考虑重要性值的波动与精度提升之间有明显的关系,当考虑重要性值波动时,精度有明显的提升,见表2。最后,使用不同方法提取重要性值波动对精度提升的效果不同,能够综合提取线性和非线性关系的MI 法相较于只能提取出线性关系的PCC 法在提取重要性值波动矩阵、提高预测精度方面具有更好的适用性。

4 结语

本文为了追踪输入特征的重要性值波动,进一步提高预测精度,提出一种考虑特征重要性值波动的MI-BILSTM 短期负荷预测方法。经过实际算例验证,得出如下结论:

1）通过对LSTM 权值共享结构的分析,发现含有循环单元的深度学习模型存在一定的局限性,具体表现在此类模型的权值不能随时间变化,无法追踪输入特征的重要程度随时间出现的波动；

2）观察输入特征重要性值波动矩阵的展示图,验证了在短期负荷预测中输入特征的重要程度会随时间的推移发生波动；

3）采用重要性值波动矩阵修正输入特征,在不增加BILSTM 模型参数的情况下,弥补了权值共享结构存在的缺陷,提高了预测精度；

4）在多种日负荷场景下,文中所提出的预测方法都表现出了更高的预测精度。这说明该方法不局限于特定场景,具备良好的自适应性和稳定性。

本文在构建输入特征时,未能将影响负荷变化的市场因素考虑在内,后续工作会构建更加丰富的输入特征。此外,本文所提模型在周末、法定节假日场景下的预测精度较低,下一步将从输入特征和模型两方面入手,进一步提高周末和法定节假日场景下的预测精度。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。