考虑环境外部性和风光出力不确定性的虚拟电厂运行优化

孙晶琪，王 愿，郭晓慧，周奕全，王玉玮，薛万磊

（1. 华北电力大学经济与管理学院,北京市 102206；2. 华北电力大学经济管理系,河北省 保定市 071003；3. 国网山东省电力公司经济技术研究院,山东省 济南市 250022）

0 引言

2020 年9 月,在第75 届联合国大会的一般性辩论上,习近平总书记作出中国“二氧化碳排放力争于2030 年前达到峰值,努力争取2060 年前实现碳中和”的重要承诺。作为中国实现“双碳”目标的关键支撑,“构建以新能源为主体的新型电力系统”不仅为电力行业的发展指明了道路,同时也对电力系统的灵活性提出了更高的要求。

虚拟电厂（VPP）是指由常规机组、可再生能源机组、储能装置和柔性负荷整合而成的电源协调管理系统［1-2］,作为能源电力系统去中心化的新兴主体［3］,VPP 能够以最佳方式集合、协调和利用不同类型的分布式电源参与电力市场和电网运行,从而增强电力系统的灵活性［4］。然而,目前关于VPP 运行优化策略的研究尚未考虑其在建设运行过程对环境造成的不良影响,优化结果对可再生能源消纳潜力的挖掘不足,制约了VPP 对“双碳”目标的助力效果,因此将环境外部性引入VPP 的调度运行中具有重要价值。

“外部性”这一术语源于1890 年马歇尔在《经济学原理》一书中“外部经济”的概念引申［5］。对于燃煤发电,其外部性至少包括2 种成本:污染物排放成本和温室气体排放对环境造成损害的成本［6］。文献［7］中使用生命周期评价方法研究了煤炭发电的环境外部性,并通过相关成本理论计算并分析了煤炭发电的能源消耗成本和环境外部成本。在新能源发展愈发成熟的阶段,一些学者以煤电环境污染物的外部性成本为基础,进而衡量风电对煤电替代的环境价值［8］,加入环境价值的风电较火电在发电成本上具有很大的成本优势［9-10］,文献［11］在光伏发电成本中也加入环境外部性进行成本上的对比,在此之后,煤电、风电以及光伏发电的外部性成本核算从污染物排放角度被加入VPP 的调度问题中［12-13］,上述研究对于风电和光伏发电的环境外部性核算大多都是正向描述的［14-15］,关于其负向环境外部性,如设备运行等发电过程中所带来的核算研究较少,并且现有的研究并未将煤电、风电和光伏发电的环境外部性的单独核算作为VPP 经济调度的一个重要因素。

由于风电和光伏发电的波动性和随机性会影响发电机组的运行状况,影响VPP 的出力稳定性。因此,考虑风电和光伏发电等可再生能源出力不确定性的调度方法在VPP 调度中尤为重要。随机优化（SO）和鲁棒优化（RO）是2 种最为常用的解决不确定性的方法,但是存在过于保守、求解效率低等问题［16-18］。一种基于Wasserstein 距离的两阶段分布鲁棒优化（DRO）模型可以有效解决上述2 种模型存在的问题［19-20］,且该模型被用来解决电-气耦合系统弹性提升优化［21］、热电联产机组的微电网日前最优运行［22］以及风-光-水-电多种能源的协同优化等问题［23］。但鲜有文献将DRO 用于VPP 中解决风光出力不确定性问题。

综上,VPP 经济调度面临环境外部性、风光出力不确定性问题。本文首先定量核算煤电、风电和光伏发电的环境外部性成本,将之引入VPP 经济调度中,进而考虑风光出力不确定性,构建基于Wasserstein 距离的VPP 的DRO 调度模型,使VPP在最优经济运行的基础上更加环保。最后,通过算例验证模型的可行性和有效性。

1 环境外部性成本模型

1.1 煤电的环境外部性成本

煤电的环境外部性成本包括环境对策成本和环境损失成本:

式中:F为年环境对策成本；F0(A/P′,ib,nY)为原始投资,其中,A为年金,P′为年金现值,ib为基准收益率,nY为电厂排污设备寿命年限；Y为年运行维护费用；Qg为煤电历史年输出功率；PE为环境损失总成本；Fei为第i种污染物的单位排放成本；Emi为第i种污染物的排放当量,中国现行火电厂以污染物当量收取排污费,即

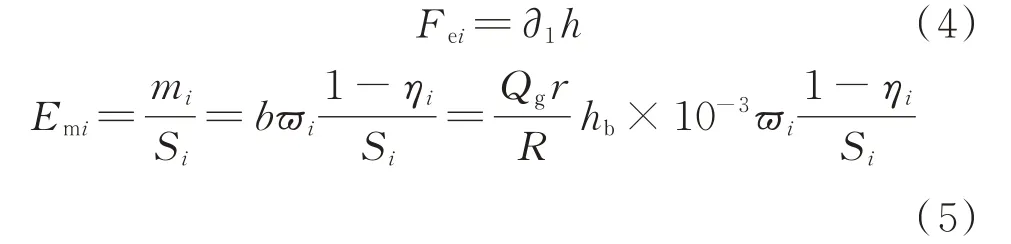
式中:∂1为排污收费标准的调整系数；h为每当量污染物应缴纳的排污费；mi为第i种污染物的排放总量；Si为第i种污染物的当量值；b为燃料消耗量；ϖi为燃煤机组对于第i种污染物的排放系数；ηi为除去第i种污染物的效率；r为发电标煤消耗率；R为原煤低位发热量；hb为标煤低位发热量,一般取值为29 310 kJ/kg。

1.2 风电和光伏发电的环境外部性成本

风电和光伏发电的环境外部性成本由环境价值成本和环境弥补成本组成,即

式中:Ui为生命周期内第i种污染物单位发电量的排放量；Vi为第i种污染物的单位环境价值；Mqj为在第q阶段的第j种材料的消耗量,可根据文献［7,24-25］求得；Dqj为在第q阶段的第j种材料的排放因子；Qwp为风电历史年发电量；I为污染物类型总数；L为全生命周期的所有阶段；J为材料总数。

光伏发电的单位发电量环境弥补成本核算与风电类似,这里不再赘述。

2 VPP 成本模型

2.1 VPP 结构

本文考虑的VPP 包括可控单元（火电、燃气轮机、燃气锅炉、余热锅炉、电制冷机、吸收式制冷机）,不可控单元（风电机组、光伏发电机组）,储能（电储能、热储能）和负荷（电负荷、冷负荷、热负荷）,符合多能互补背景下VPP 的发展趋势。一方面,可控单元和储能可用于平抑不可控单元出力的波动性,使VPP 达到整体可控,并提高调度的灵活性；另一方面,燃气轮机等能量转换设备可以提高能源的利用效率,一定程度上能减小VPP 的环境外部性成本。

VPP 中的电负荷由火电、燃气轮机、电储能、风电机组和光伏发电机组供给；冷负荷由电制冷机和吸收式制冷机供给；热负荷由燃气锅炉、余热锅炉和热储能供给。VPP 的具体结构如附录A 图A1 所示,图中箭头为能量流动方向。

2.2 目标函数

2.3 第1 阶段约束条件

VPP 实际运行中存在弃风和弃光现象,且风电和光伏发电具有较强的不确定性,为应对此问题,在第2 阶段成本中引入弃风和弃光惩罚成本并采用DRO 模型进行建模求解。

3 DRO 模型

将风光出力的历史数据拟合得到其出力分布函数,从而构造合适的模糊集。一个恰当的模糊集应涵盖所有潜在风光出力的真实概率分布［26-27］。基于Wasserstein 距离构建的模糊集假设包含所有可能的概率分布,并具有置信水平,且随着历史数据的增加,此集合保证未知分布收敛到真实分布,有效解决VPP 中风光出力不确定性的问题。

3.1 风光出力不确定集合构建

式中:ρ表示一个大于0 的数；μ^ 为样本均值。

3.2 数据驱动不确定集

给定样本集合{ω^1,ω^2,…,ω^N}一个支持集Ξ,对样本标准化处理得:

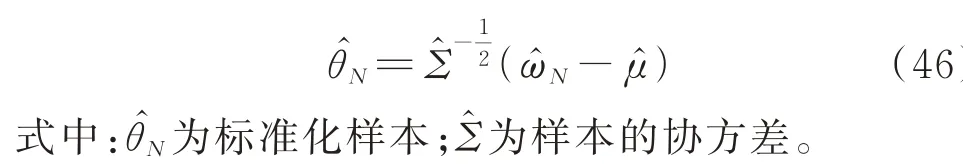
3.3 第2 阶段模型转化

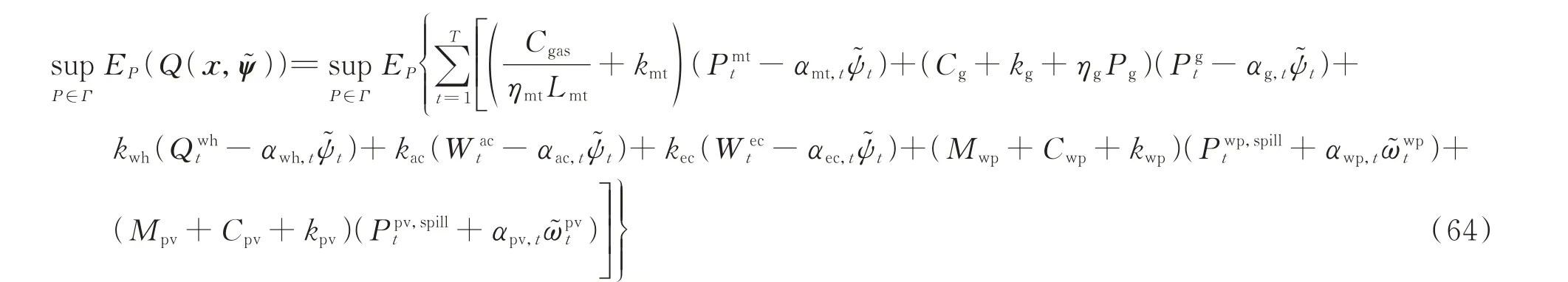
式中:[Cgas/(ηmtLmt)](Pmtt-αmt,tψ～t)为t时段燃气轮机的燃料成本；kmt、kg、kwh、kac、kec、kwp、kpv分别为燃气轮机、火电机组、余热锅炉、吸收式制冷机、电制冷机、风电机组和光伏发电机组的单位运维成本；ηg为单位发电量燃煤消耗率；Pg为燃煤价格；Mwp为单位发电量弃风惩罚成本系数；Mpv为单位发电量弃光惩罚成本系数。

第2 阶段约束条件以弃风和弃光约束为例,如式（65）所示。式（65）为考虑风光出力误差后的出力约束条件,其余机组约束条件见附录A 式（A1）—式（A15）。

3.4 模型求解

4 算例仿真以及对比分析

4.1 环境外部性成本核算

算例数据来自国内某实际运行VPP,其中,煤电、风电、光伏发电机组装机容量分别为300 MW、47.5 MW、1 MW,详细参数见附录A 表A1 至表A3。计算得出煤电单位环境损失成本为0.37元/（MW·h）；单位环境对策成本为26 元/（MW·h）；单位环境外部性成本为26.37 元/（MW·h）。

风电和光伏发电生命周期内的污染物排放量以及污染物排放强度计算结果分别见表1 和表2。风电和光伏发电的单位环境外部性成本计算结果见表3。

表1 全生命周期内各个污染物排放量Table 1 Emissions of various pollutants throughout whole life cycle

表2 全生命周期内污染物排放强度Table 2 Pollutant emission intensity throughout whole life cycle

表3 风电和光伏发电的单位发电环境外部性成本Table 3 Environmental externality cost per unit of power generation of wind and photovoltaic power

4.2 优化模型数据来源

算例中风电和光伏发电的数据取自PJM 的公开数据［28］；系统初始负荷及风光出力预测曲线如附录A 图A2 和图A3 所示,模型将在附录A 图A1 所示VPP 上进行仿真,调度的周期为1 d,分为24 个时段,各个机组的具体参数见表A4。

在原始数据和上述所提DRO 模型的基础上,采用MATLAB R2016b 软件CPLEX 和Yalmip 求解器,在操作系统为Windows10 64 bit,内存为8.0 GB,CPU 为Intel Core i5 的电脑上进行仿真,时间为3.631 s。优化所得VPP 最优成本为1.53×106元,火电机组、燃气轮机、电制冷机输入、电储能充放电以及弃风和弃光出力方案如图1 所示,VPP 内部余热锅炉、燃气锅炉、电制冷机输出、吸收式制冷机、热储能吸放热方案如图2 所示。

图1 最优电力调度Fig.1 Optimal electricity dispatch

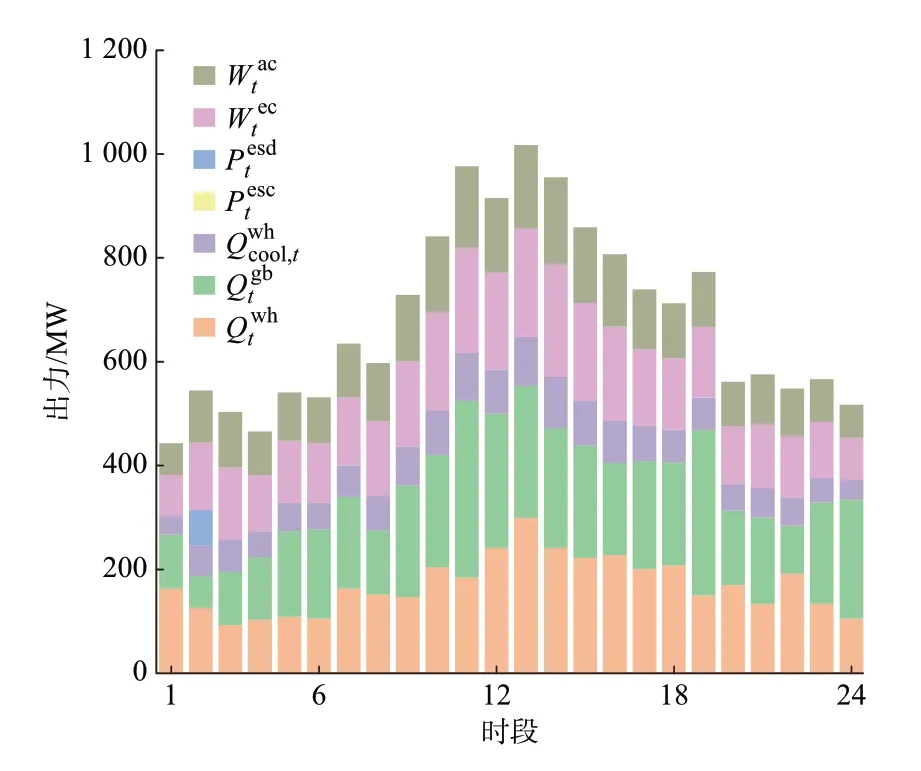
图2 最优冷热调度Fig.2 Optimal heat and cooling scheduling

根据图1 和图2 以及附录A 图A2 所示负荷曲线可知:各个机组出力调度趋势符合系统负荷需求。火电机组和燃气轮机是系统电能的主要来源,火电机组和燃气轮机的功率在时段10 至12 升高是由于系统电负荷在时段12 左右达到最高峰；在时段1 至6、时段17 至24,风电功率逐渐升高,系统电负荷降低,电储能的充电功率相应增加以满足电负荷的平衡。

在时段19 至24,冷负荷逐渐降低,吸收式制冷机以及电制冷机基本保持在最低输出功率,电制冷机的单位运行维护费用较低,因此可以提供更大输出功率以满足冷负荷的需求。

在时段7 之前,系统热负荷增加缓慢,热负荷需求由燃气锅炉的输出功率满足,并且在时段10 左右输出功率最高；在时段21 至23,系统电、热负荷降低,受燃气轮机热电耦合性的影响,余热锅炉输出功率相应降低,燃气锅炉功率升高以达到系统热平衡。

4.3 不同情景下的优化结果对比分析

为验证考虑环境外部性和风光出力不确定性的DRO 模型的优越性,设置以下4 种情景进行对比仿真,对比结果见表4、图3 至图6。

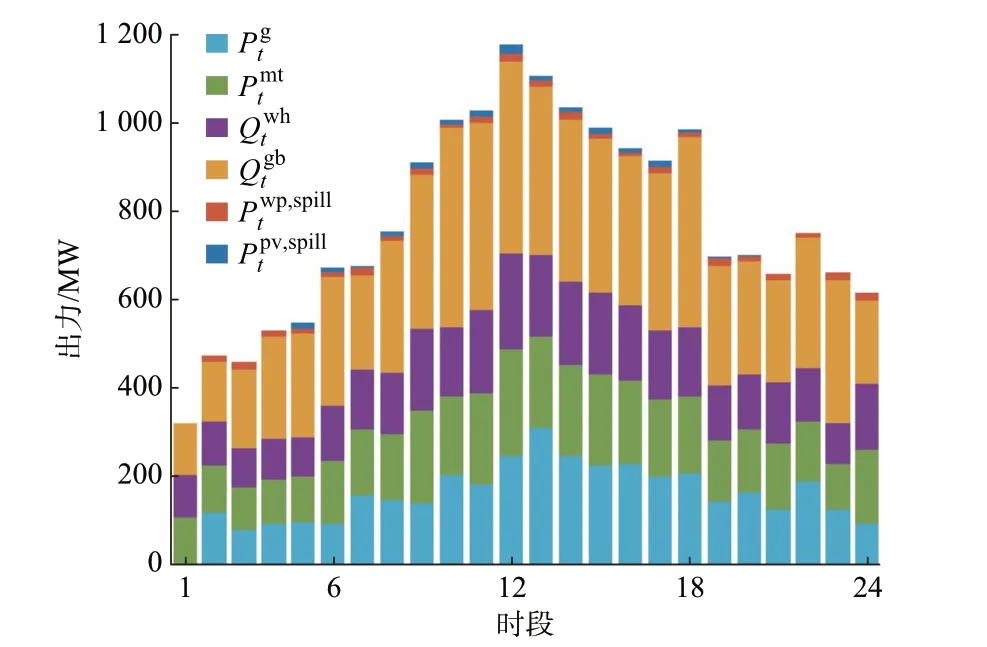
图3 情景1 机组24 h 出力Fig.3 24-hour output of unit in scenario 1

图4 情景2 机组24 h 出力Fig.4 24-hour output of unit in scenario 2

图5 情景3 机组24 h 出力Fig.5 24-hour output of unit in scenario 3

图6 情景4 机组24 h 出力Fig.6 24-hour output of unit in scenario 4

表4 不同情景下VPP 各机组及系统最优成本Table 4 Optimal cost of units and systems in VPP in different scenarios

情景1:不考虑环境外部性的确定性模型。

情景2:考虑环境外部性的确定性模型。

情景3:不考虑环境外部性的DRO 模型。

情景4:考虑环境外部性的DRO 模型（本文所提模型）。

根据表4、图3 至图6 中不同情景下典型机组24 h 出力可以得出如下结论。

考虑环境外部性之后,情景2 相较于情景1 的火电机组出力降低,风电、光伏发电机组出力升高,风电和光伏发电的总成本降低是由于其单位环境外部性成本为负,火电的环境外部性成本以及单位运维成本较高导致机组出力降低,燃气轮机出力升高使系统电负荷达到平衡,燃气锅炉出力降低进而满足系统热负荷的平衡,VPP 最优成本降低7.27%。同样地,情景4 相较于情景3 的风电和光伏发电的利用率得到提升,VPP 最优成本降低9.14%。

对比情景4（本文所提模型）与情景2,分析考虑风光出力不确定性对VPP 优化运行的影响。由于风电和光伏发电的波动性造成在情景2 下得到的VPP 最优成本较高,而在情景4 中,DRO 模型充分利用风光出力的历史数据,采用Wasserstein 球限制风光出力概率分布的波动范围,使得系统最大限度地提高风电和光伏发电的利用率,风光出力增加使得其成本升高,火电出力有所降低使得其最优成本降低36.44%,燃气轮机、电制冷机等柔性资源的出力升高促进风电和光伏发电的消纳,VPP 最优成本降低9.26%。情景3 与情景1 相比较最优成本同样有所下降。

情景1 和情景4 相比,在情景4 中,同时考虑环境外部性、风光出力不确定性,火电的成本降低44.47%,风电和光伏发电的利用率显著提升,系统的最优成本降低36.07%。

综上所述,引入环境外部性处理VPP 运行中的污染问题,并运用DRO 模型解决风光出力的不确定性,能够降低火电的输出功率,充分发挥风电和光伏发电的能源优势,使VPP 在最优经济运行的基础上更加环保,从而为推进“双碳”目标与能源体系建设的融合提供策略依据。

4.4 不同优化模型的结果对比分析

本文所提模型用于解决风光出力的不确定性,为验证模型的适用性以及优越性,将其与SO 和RO模型进行对比分析,RO 和SO 模型参考文献［17］,不同样本量下3 种模型的最优成本和求解时间分别如表5 和表6 所示。

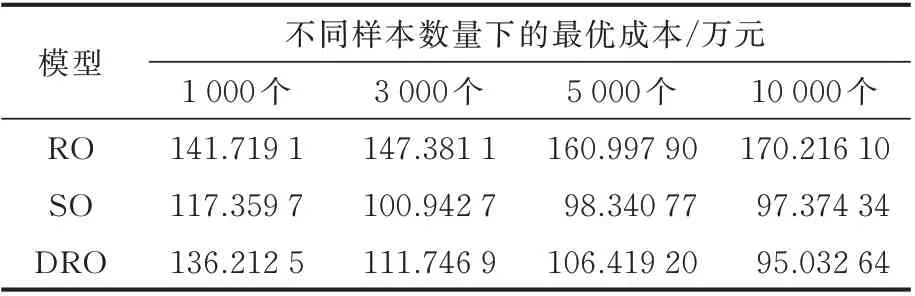
表5 不同样本量下3 种模型的最优成本Table 5 Optimal cost of three models with different sample sizes

表6 不同样本量下3 种模型的求解时间Table 6 Solution time of three models with different sample sizes

如表5 所示,当样本量为1 000 个时,DRO 的最优成本与RO 的最优成本相差不大。由于RO 考虑环境最恶劣时的成本最小,因此随着样本数量的增加,RO 的成本越来越高,但是环境出现恶劣情况的概率极低,RO 具有一定的保守性。而DRO 模型考虑了风电和光伏发电不确定性的分布特性,针对概率极低的极端场景不会采用大量资源来应对,从而使结果的保守性较小。在样本量足够大时,DRO 的成本和SO 的成本相差不大,DRO 趋近于SO,但如表6 所示,随着样本量的增加,SO 的求解时间远远高于DRO。根据上述分析可知,所提模型避免了SO 求解效率低、RO 保守的问题,同时考虑了风光出力的不确定性,模型求解时间较短,更具有一定的代表性和适用性。

5 结语

本文对煤电、风电和光伏发电的环境外部性进行了单独核算,并将其纳入VPP 的运行成本。在此基础上,进一步考虑风光出力不确定性的干扰,构建了基于Wasserstein 距离的风光出力预测误差模糊集的两阶段DRO 模型,研究VPP 的运行优化问题,所得结论如下:

1）考虑环境外部性、风光出力不确定性之后,VPP 中风电和光伏发电的能源利用效率提升,火电的发电量有所下降,系统最优成本降低36.07%,符合“双碳”目标下构建清洁低碳、安全高效的能源体系的政策导向。

2）将本文提出的DRO 模型与SO 模型、RO 模型相对比,一方面,DRO 模型能够克服RO 模型过度保守的问题,从而在风光出力不确定性的干扰下,改善VPP 运行的经济性,另一方面,DRO 模型的运行简便性优于SO 模型,较短的运行时间确保了其在实践中的可行性。

大规模可再生能源的接入及其出力的不确定性增加了灵活性资源的需求,如何在VPP 中将煤电等机组参与辅助服务的灵活性价值计入调度模型以保证系统整体的运行灵活性,是后续研究工作的重点。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。