拖锥系统管路延迟时间分析研究

姜延欢，吴娅辉，杨军，刘渊，谢兴娟，田森

（航空工业北京长城计量测试技术研究所计量与校准技术重点实验室，北京 100095）

0 引言

准确可靠的静压是飞机计算空速、高度的重要参数，常用的静压测量方法主要有GPS参考高度法、真空膜盒气压计法、拖锥法等。然而，除拖锥以外的几种试飞方法大多存在校准精度难以满足国际适航认证等缺点。拖锥系统主要通过安装在飞机内部的收放机构将拖锥放到飞机尾部后1～2倍展翼位置处，通过静压管上的静压孔将空气引入管内进行测量，能够避免机身附近复杂流场的影响［1］，实现静压的准确测量，进而确保飞行高度和飞行速度的准确测量［2］，因而广泛地适用于各种飞行测试。不足之处在于拖锥导管与压力传感器之间的距离较长，引起拖锥系统的时间延迟严重。因此，对拖锥系统的延迟时间进行深入分析，确定其影响在测量系统精度容许范围内，是保证拖锥测量数据有效性的必要条件［3-4］。

拖锥系统的概念模型最早由道格拉斯飞机公司于1959年提出［5］，对于飞行中的飞机而言，拖锥系统管路的长度超出一定翼展后，静压场将不受飞机周围的流场干扰［6］，可以测得稳定的静压。随后，道格拉斯飞机公司、皇家航空机构、海军测试中心、联邦航空局和美国国家航空咨询委员会均对拖锥系统进行了设计及测试。美国国家航空咨询委员会在针对空速的测量精度和测量程序的研究中指出，粘性延迟随飞机飞行高度、垂直下降速度和拖锥软管长度增加而增大，但与软管直径成反比［7］。

目前，针对拖锥系统管路压力时间延迟的理论研究主要有两种方法：一种是基于压力管路的动态特性研究系统的迟滞特性，从而确定系统的迟滞指标；另一种是基于小扰动理论推导出管路的静压延迟时间。

中国商飞上海飞机设计研究院的宋歌［8］基于所建立的管路模型，并结合流体力学中的哈根-泊肃叶（Hagen-Poiseuille）流动公式，得到静压延迟时间的理论模型，为了便于分析，其假设空速系统中的所有管路均为直管路，并将带有管路的空速系统等效为一阶系统，推导出管路的静压延迟时间。

航空工业成飞的李南伯［9］针对民机适航试飞静压测试中的静压校准计算机误差分析进行了研究，考虑到声学延迟的影响比重较小，故仅考虑了黏性延迟的影响，给出了拖锥系统管路中由黏性延迟引起的压差计算方法。

航空工业洪都650所的汤黄华［10］基于JL8飞机的静压系统开展研究，将静压系统简化为包含进气管和泄气管的容器，对静压系统施加阶跃压力信号，获得系统压力的响应规律，从而确定系统进气和泄气过程中的迟滞指标。

宁波大学的朱国瑞［11］在针对航空器压力测量管路的迟滞特性进行理论研究时，基于小扰动假设，将管路内的流动简化为一维层流的准定常流动，同时忽略运动方程中的惯性力项及管内气流的径向运动，在流动为等温过程、管路入口为等速率变化时，得到粘性压力滞后，但是该公式只能在层流条件下才能够很好地预测管路的滞后特性，且适用于管长与管径比l/D=102～103的范围。

综上所述，在对管路的延迟时间开展理论研究时，考虑到模型本身的复杂性及计算的成本，将管路系统简化为一阶系统，并基于连续方程和动量方程对管路系统从时域建模是常用的方法。虽然简化后的模型仍能够对工程设计进行理论指导，但是往往都有其特殊的应用范围，这主要还是因为模型过度简化导致模型的预测能力降低。对于拖锥系统而言，飞机的飞行工况复杂，加之拖锥系统自身包含超长的管路，使得管路内的流动也随之变得复杂，将管路系统简化为一阶系统无法真实反映其管路延迟时间。基于时域的建模方法则需要重点考虑管路摩擦力造成的粘性延迟对压力响应迟滞的影响，进而实现拖锥系统延迟时间的准确预测。为此，本文基于连续性方程和动量守恒方程对拖锥系统管路系统进行建模，并在此基础上研究管路结构参数和环境参数对拖锥系统管路时间延迟的影响规律。

1 拖锥系统管路建模

管路中可压牛顿流体流动过程的建模主要考虑连续性方程和动量守恒方程。连续性方程假设流体为连续介质模型，流体宏观物理量是空间点及时间的连续函数。对拖锥系统压力延迟的模拟主要是研究系统内的流动和压力分布状况，并作出如下假设：①拖锥系统管路中的气体介质满足连续性介质假设；②管路内的气体满足理想气体状态方程；③拖锥系统的管路为绝热，管路内部气体介质与外界环境之间不存在热传递［12］；④管路内部气体流动径向的空间梯度忽略不计，即流动被认为是一维的［13］；⑤流体性质在横截面上取平均值，并且仅取决于轴向位置和时间［14］；⑥管路中气体的流动方向垂直于重力加速度方向，因此，忽略重力的影响。

连续性方程为

式中：ρ为拖锥系统中可压缩气体介质的密度，kg/m3；u为气流速度，m/s；t为时间，s；z为管道沿轴线的位置，m。

为了能够更准确地描述拖锥系统气体压力延迟过程，必须考虑管路璧产生的摩擦力，包含摩擦力的动量守恒方程为

式中：fc为可压缩摩擦因子；D为管路直径；p为气体介质的压力。管路中的气体满足理想气体状态方程，即p=ρRgT。其中Rg为空气的气体常数，J/（kg·K）；T为介质的温度，K。管路内的压降Δp可通过Darcy-Weisbach公式计算，即

不可压缩流的Darcy摩擦因子f和可压缩摩擦因子之间存在如下关系

式中：γ为比热比；Ma为马赫数，Ma=u a，其中声速a的计算方式为

Darcy摩擦因子f是计算管路中摩擦力的主要参数，当管路内的流动为层流时，f可通过如下公式计算［15］

式中：Re为流动的雷诺数，其计算方法为

式中：η为气体介质的动力粘性系数，N·s/m2。

当管路中为湍流时，f可通过Haaland方程进行计算［15］

式中：ε为管路璧面的绝对粗糙度，m。

当管路中的气体介质由层流向湍流转变时（即Recr，min＜Re＜Recr，max），f可通过差值进行求解。当流体由层流向湍流转变时，Re的临界值Recr，min和Recr，max的计算为［15］

综上所述，本文所构建的管路模型考虑了层流、层流向湍流转变及湍流三种不同的流动状态，适用性更强。在求解的过程中，时间项的离散格式为全隐式，密度项的离散格式为一阶迎风，速度项的离散格式为中心差分与一阶迎风的混合格式；时间步长定为0.000 01 s，管路的璧面粗糙度为1.5×10-5m。

2 模型验证

为了验证理论计算的准确性，选用激波管产生标准阶跃压力信号，试验所采用的激波管能够产生非常理想的阶跃式压力，阶跃压力上升时间小于等于1μs。所采用的试验装置如图1所示。

图1 阶跃压力发生装置Fig.1 Step pressure generating device

基于阶跃压力校准装置对计算结果进行验证。在试验的过程中，在激波管末端安装标准传感器，通过工装在管路系统及其末端安装被校传感器，最后由数据采集系统完成标准传感器和被校传感器信号的采集。在试验的过程中需要保持管路水平，避免管路弯曲造成的压力损失。

图2 激波管末端传感器及信号采集系统Fig.2 Sensor at the end of the shock tube and signal acquisition system

在对数据进行采样时，采样率设置为5 MHz。通过对比标准传感器和被校传感器测得的压力信号，得到管路的延迟时间。由图3可以看出，理论计算得到的理论延迟时间与试验差别较小。

图3 理论及试验对比Fig.3 Comparison of theory and experiment

同时选取管长为5 m时管路末端压力信号的幅值进行仿真，为了确保试验信号与仿真信号的可比性，仿真过程中的激励信号采用被校传感器的波形。由图4可以看出，仿真波形与试验波形整体的符合程度较好。

图4 理论信号与试验信号波形归一化比对Fig.4 Normalized comparison of theoretical signal and experimental signal waveform

3 结果和讨论

3.1 管路长度对拖锥系统延迟时间的影响研究

管长是影响拖锥系统延迟时间的核心因素，为了明确管路长度对拖锥系统延迟时间的影响规律，项目选取管长分别为5，10，20，40，60 m和80 m。对比不同管长条件下，阶跃压力信号传递至管路端面时的压力分布曲线可以看出：管路长度对压力信号的分布主要体现在压力上升时刻、压力峰值和压力波形三个方面。如图5所示，当管路直径小于20 m时阶跃信号的峰值会显著放大，大于初始阶跃信号的压力；当管路直径大于20 m时阶跃信号的峰值显著降低，压力波形也呈现出明显的双峰形状。

图5 管长对拖锥管路中压力的影响Fig.5 Effect of pipe length on the pressure in the pipe of trailing cone system

随着拖锥系统管路长度的增大，拖锥系统管路的延迟时间呈现出线性增长的趋势。压力波传播所需要的延迟时间增大，此外，管路璧对流体产生的阻力也急剧增大。在两种延迟机理的共同作用下，拖锥系统管路的延迟时间迅速增大，如图6所示。

图6 管长对拖锥管路中压力延迟时间的影响Fig.6 Effect of pipe length on the delay time of pressure in the pipe of trailing cone system

3.2 管路直径对拖锥系统延迟时间的影响研究

为了研究管路直径对拖锥系统延迟时间的影响，在长度为80 m的管路入口处施加50 kPa的阶跃压力，分析管路末端的动态压力特性，进而测得拖锥系统管路的压力延迟时间。不同管路直径下管路中的压力曲线形状相似，随着管路直径的增大，管路中的压力整体增大，压力迅速升高，所对应的时刻提前，压力曲线第一个峰值与第二个峰值的比值不断增大。当管径为12 mm时，第一个压力峰值明显超过第二个压力峰值，如图7所示。

图7 管径对拖锥管路压力的影响Fig.7 Effect of pipe diameter on the pressure in the pipe of trailing cone system

随着管路直径的增大，拖锥系统管路延迟时间呈现出非线性降低的趋势，管路直径为6 mm时，出现明显的拐点，如图8所示。这主要是由于随着管路直径的增大，粘性阻力造成的延迟时间的比重逐渐降低引起的。

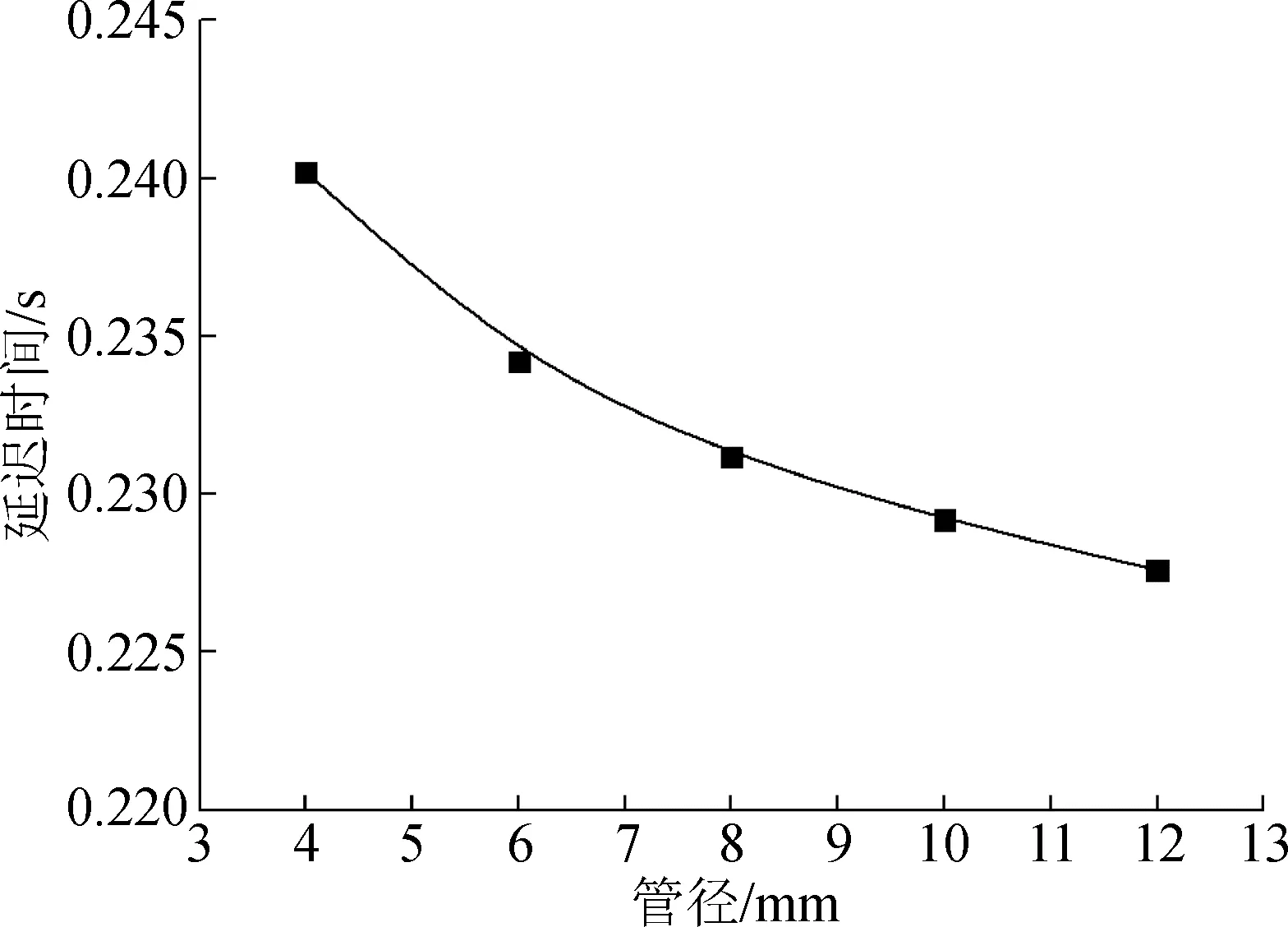
图8 管径对管路延迟时间的影响Fig.8 Effect of pipe diameter on the delay time of pipe

3.3 阶跃压力对拖锥系统延迟时间的影响研究

选取阶跃压力分别为10，30，50，70，90 kPa，研究阶跃信号的阶跃压力对拖锥系统管路压力分布的影响规律。可以看出，随着阶跃压力的增大，管路末端的压力整体增大，压力信号的脉宽逐渐增大，压力信号第一峰值和第二峰值的比值逐渐降低。当阶跃压力为90 kPa时，压力信号的第一峰值显著低于第二峰值，如图9所示。

图9 阶跃压力对拖锥管路压力的影响Fig.9 Effect of step pressure on the pressure in the pipe of trailing cone system

由阶跃压力对拖锥管路延迟时间的影响可以看出，随着阶跃压力的增大，延迟时间呈现出非线性降低的趋势。这主要是由于阶跃压力的提升，增大了压力波在管路中传播的速度，声学延迟时间显著降低，然而由于速度的增大，显著增强了管路璧对气流的粘性阻力，由粘性引起的延迟时间增大，但延迟时间由声学延迟时间主导，如图10所示。

图10 阶跃压力对管路延迟时间的影响Fig.10 Effect of step pressure on the delay time of pipe

3.4 环境背压对拖锥系统延迟时间的影响研究

在具体的飞行过程中，飞机需要适应不同海拔的变化，其环境背压也在不断变化。对比不同环境背压下管路端面的压力分布，压力分布的曲线形状差别整体较小，压力波形的脉宽、峰值差别不大，如图11所示。

图11 环境背压对拖锥管路压力的影响Fig.11 Effect of ambient pressure on the pressure in the pipe of trailing cone system

由环境背压对管路延迟时间的影响可以看出，随着环境背压的增大，拖锥系统管路的延迟时间整体呈现出增大的趋势。由于在仿真过程中阶跃压力保持一致，环境背压的变化直接引起管路中气体自身属性的变化。随着环境背压的增大，管路中气体的比热比增大，导致当地声速增大，声学延迟降低；与此同时，密度增大，管路由于粘性产生的阻力增大。最终的综合效果导致管路的延迟时间随着环境背压的增大而增大，如图12所示。

图12 环境背压对管路延迟时间的影响Fig.12 Effect of ambient pressure on the delay time of pipe

3.5 环境温度对拖锥系统延迟时间的影响研究

为了模拟飞机飞行环境中环境温度对拖锥系统管路延迟时间的影响，选取环境温度分别为233.15，253.15，273.15，293.15 K和313.15 K。环境温度对拖锥管路末端压力分布曲线形状的影响主要体现在信号脉宽、压力曲线的第一和第二峰值上。如图13所示，随着环境温度的增大，第一压力峰值呈现出降低的趋势，第二压力峰值呈现出增大的趋势，但是变化幅值均不大。

图13 环境温度对拖锥管路末端压力的影响Fig.13 Effect of ambient temperature on the pressure at the end of thepipe of trailing cone system

如图14所示，随着环境温度的升高，拖锥系统延迟时间呈现出非线性降低的趋势，这主要是由于随着环境温度的升高，压力波传播的速度增大，粘性产生的阻力也降低，声学延迟和粘性延迟均降低。

图14 环境温度对管路延迟时间的影响Fig.14 Effect of ambient temperature on the delay time of pipe

4 结论

拖锥系统管路压力延迟的快速、高精度预测是确保飞行安全的基础。本文提出了一种基于连续性方程和动量方程对拖锥管路中的可压牛顿流体流动过程进行理论建模的方法，同时重点考虑了管路璧面粘性阻力对管路时间延迟的影响因素，更加贴近真实工况。通过与激波管试验进行比对，验证了所构建模型的准确性，在此基础上，研究了管路结构参数和环境参数对管路时间延迟的影响规律，随着拖锥系统管路长度、环境背压的增大，管路末端阶跃压力的峰值逐渐降低，拖锥系统管路的延迟时间呈现出线性增长的趋势。随着管路直径、阶跃压力的增大，管路末端的压力增大，拖锥系统管路的延迟时间呈现出非线性下降的趋势。随着环境温度的增大，拖锥系统管路的延迟时间呈现出非线性下降的趋势。