11辊矫直机压下量与板材初始参数的关系研究
段勋兴,谭正生,刘志芳
(1.重庆化工职业学院 智能制造与汽车学院,重庆 400812;2.重庆理工大学 机械工程学院,重庆 400050)
0 前言
板材在车辆、船舶、桥梁 航空航天等领域应用广泛。然而,在其生产过程中,由于板厚不均、温度变化和冷却相变差异等原因可能会产生弯曲、中波和边波等板形缺陷,因此需要通过矫直工序来消减板形缺陷和控制残余应力,才能最终实现板材的高质量生产[1]。辊系压下量是矫直工艺中至关重要的参数,它需要根据板材的厚度、屈服极限和弹性模量等初始参数计算,研究压下量与板材来料初始参数之间的内在关系,对于矫直机在线工艺参数的设置十分重要。
近年来,很多学者采用各种手段研究了压下量的求解方法。宋浩[2]建立了双金属复合板在矫直过程中的有限元模型,分析了复合板在矫直过程中不同压下规程下纵向位移的变化规律以及对残余应力的影响。王若然[3]模拟了1 800 mm大型型钢矫直机在矫直过程中其压下量对矫直质量的影响。宋小平[4]通过分析板材在矫直过程中塑性变形率、各矫直辊下板材相应曲率和压下量三者间关系,获取一种计算矫直辊压下量的简化方法。张立杰[5]通过数值模拟对比了大变形、小变形、小倾角整体倾斜、大倾角整体倾斜4种矫直方案中钢板的残留挠度和残余应力,并分析了矫直速度对矫直过程的影响。李中喜[6]采用有限元软件研究了金属带材边浪的生成及拉伸弯曲矫直过程,为生产现场选取较佳的矫直工艺参数提供帮助。此方法精度较高,但计算时间成本较高。殷璟[7]以出口残余曲率为零为目标函数,建立了正向求解理论压下量与残余曲率关系的多辊矫直解析模型,计算结果表明单个辊系的挠曲线可以用余弦函数的形式表示。张赵宁[8]分析出了不同的目标曲率、伸长率下张力和压弯量的配置关系。王效岗[9]将大变形平行辊缝矫直方案应用于高强板矫直实践中,并建立边辊调整计算方法,通过实验方法对大变形平行辊缝矫直方案进行验证。李董超[10]通过有限元软件分析研究了不同张力下矫直辊压下量对板形瓢曲的影响程度,并在两弯一矫型式的拉伸弯曲矫直机上进行了实验分析。王勇勤[11]建立了矫直压下参数与中厚板原始参数之间关系的优化模型,优化结果与现场的数据保持了较好的一致性,但是由于每次优化仍然需要数秒的时间,不适合现场在线应用。Guan[12]基于曲率积分法研究了如何针对随机原始曲率的板材进行矫直的研究。Zhang[13]基于分析了张力和弯曲综合效果在带钢张力矫直过程中的效果。
本文探讨压下量与板材初始参数之间的内在联系,并进行现场数据的验证。
1 压下量与板材来料初始参数的关系
本文研究的单变量初始参数是指板材来料的厚度、屈服极限、弹性模量。目前曲率积分法是描述矫直过程的有效方法[14],其特点在于该方法将板材与矫直辊的接触点位置设为未知量,并与矫直辊弯曲曲率进行解耦求解。王勇勤等已经提出了高效的求解方法并开展了工艺参数优化求解[11,14],本文主要引用他们的模型和方法分析压下量与板材来料初始参数的关系。
以某钢铁企业生产线的11辊矫直机为例,上辊直径为285 mm、辊距为300 mm,该设备由四个油缸实现压下量的设定,并配有弯辊系统用于消除弹性变形和实现正负弯辊凸度。从操作简化的角度出发,尾辊压下量很多品种均设置为0,即如果能够只调整首辊压下量,则辊系压下量可以按照线性递减的方法确定。以生产线中材料编号为A572Gr50的板材为例,将板材厚度从5 mm变化到30 mm,在满足最大塑性变形率[pl]达到75%和出口平直度为2 mm/m的条件下,不断调整压下量δ2,得到如图1所示关系。压下量与弹性模量和屈服极限的关系如图2和图3所示。对比分析发现:压下量δ2与厚度的关系呈现单调递减的非线性关系,与屈服极限呈现单调递增的线性关系,与弹性模量呈现单调递减的不明显非线性关系。
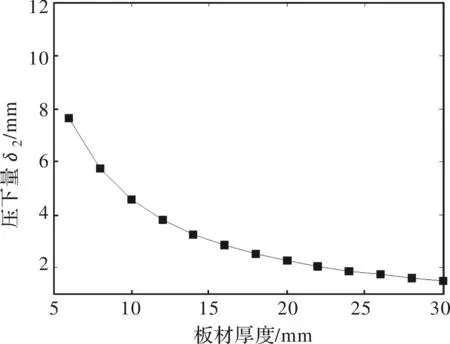
E=127 510 MPa,δs=195.7 MPa,[pl]=75%图1 压下量δ2与板材来料厚度H的关系

E=127 510 MPa,H=30 mm,[pl]=75%图2 压下量与板材来料屈服极限的关系
数据处理时发现,将屈服极限、弹性模量E和厚度H合并为一个变量,即:κt=2σs/EH,则压下量δ2与κt的关系如图4所示,三条曲线基本重合,这说明无论板材来料屈服极限、弹性模量和厚度如何变化,只要保持它们的κt不变,则压下量就可以不变,这对于快速设置压下量非常有利。弹性极限曲率的含义是,如果板材初始曲率为κt,则将其反弯到曲率为0时,板材边层刚好处于弹塑性状态的边界状态,所需要的弯矩为弹性极限弯矩Mt=B×H2×σs/6,其中B为板材宽度,H为板材厚度。
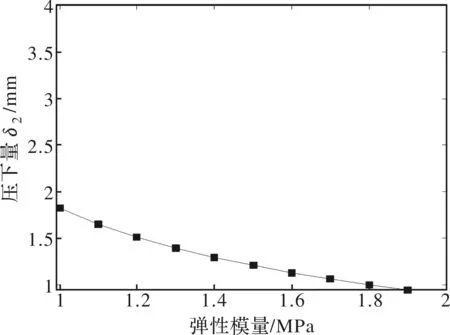
σs=195.7 MPa,H=30 mm,[pl]=75%图3 压下量与板材来料弹性模量的关系

图4 压下量与弹性极限曲率的关系
2 数值模拟结果与现场数据的对比验证
根据本文研究,从生产线上随机找到一个材料为AB/AH32的板材,该板材的参数见表1。

表1 板材来料原始参数
计算该规格板材的弹性极限曲率κt为0.105 7,在图4曲线中进行差值得到压下量δ2为1.604 6。为了验证该结果的可靠性,借助MSC.Marc有限元软件进行非线性接触有限元仿真,有限元模型如图5所示,矫直辊均设置为刚体,板材设置为变形体,单元类型为4节点平面应变单元,沿着厚度方向划分了4层单元,下排辊只有旋转运动,上辊辊的压下量分别为1.604 6、1.203 5、0.802 3、0.401 2、0,上排辊先压下,然后所有矫直辊同步旋转,依靠摩擦力将板材送入辊缝进行矫直。
图6所示为矫后效果,图7为解析法、现场数据和有限元计算的各个矫直辊的矫直力分布,通过对比发现,他们具有较好的一致性,由此可见,本文研究的压下量与板材原始尺寸之间的关系具有较好的可靠性,适合现场在线设置辊系压下量。
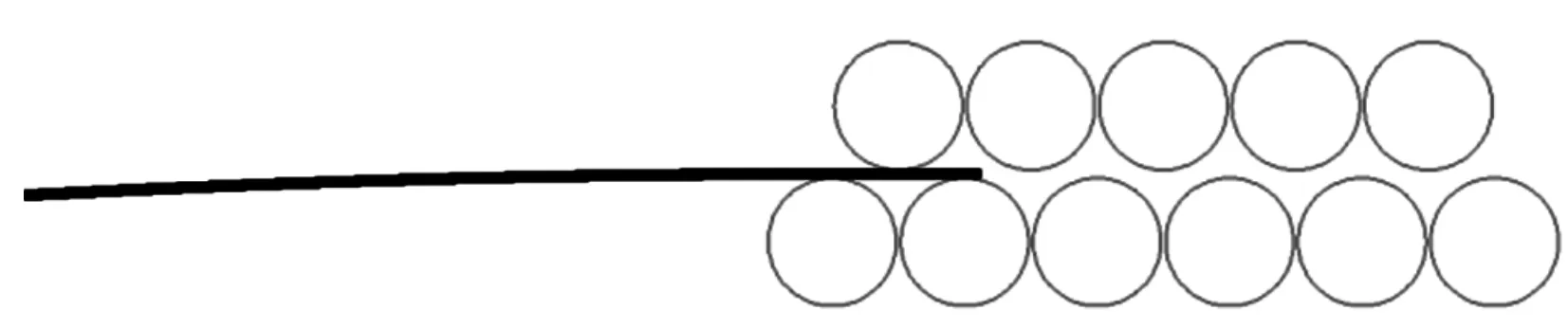
图5 有限元模型
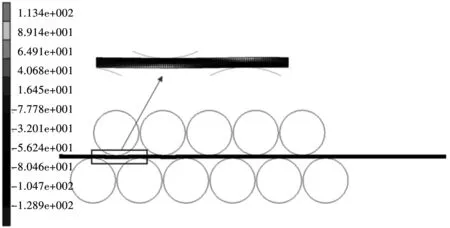
图6 矫直仿真效果

图7 矫直力的对比
3 结论
(1)压下量与厚度呈现非线性关系、与屈服极限呈现线性关系、与弹性模量呈现不明显的非线性关系。
(2)无论板材来料参数如何变化,只要其弹性极限曲率不变,压下量可以设置成相同参数。
(3)板材的合理压下量可以通过压下量与弹性极限曲率的关系曲线快速差值获得,从而用于在线工艺参数设定。

