基于改进前馈补偿模糊PID的随动特性分析

彭 斌，王文奎，马军祥，冶 振

(1. 兰州理工大学，甘肃 兰州 730050；2. 航空工业兰州万里航空机电有限责任公司，甘肃 兰州 620100)

1 引言

一般客机在夜间地面滑行时凭借固定式安装滑行灯照亮前方道面，在转弯过程中会出现内侧视线盲区。为了满足飞机驾驶员对前方照明条件的主观需求，在转弯时扩大其视野，提高驾驶安全性，提出了一种能够实现随动转向的智能滑行灯控制系统。同时，SAE-ARP693规范对滑行灯和跑道转弯灯在飞行员前方和侧方都有具体的照度要求[1]，但跑道转弯灯分布于左右两侧，安装在前起落架或翼根部位，总和机身主轴线呈一定角度[2]，这样虽然扩大了视野，但不免会在停机坪或其它滑行场地给周围人造成炫目感。基于此，该系统在满足照明要求的情况下可减少照明设备同时还能避免眩光。

控制算法作为伺服系统的核心。考虑到自适应模糊神经网络控制和借助于线路基础数据库的离线分析法等需要基于大量的训练样本和基础数据库才可取得较为理想的稳定性和自适应能力，延长了线下研发周期[3]。而在线控制中模糊控制作为一种基于专家经验、将模糊理论转化为可数学实现的控制算法，虽然具有极强鲁棒性，但在响应速率和稳态精度上有待改进[4]。PID控制作为经典的线性控制法，因固定的参数难以兼顾动静态特性，抗扰动性不足[5～7]。 于是，将模糊理论和PID控制相结合可以兼顾鲁棒性和精确性[8]，但经过试验发现该算法在低转速系统中开始响应阶段出现局部过灵敏、容易发散的现象，当改变摩擦系数会出现较严重的震荡现象，其论域的适应范围较窄。

在低速伺服系统中，摩擦现象无疑是影响系统响应的最主要因素之一，而摩擦补偿技术又分为固定摩擦模型补偿、基于部分摩擦特性的补偿和基于变参数摩擦模型的自适应补偿。薛进学在牙科CT转台上应用到了的摩擦补偿策略[9]，有效地改进了转台系统低速带来非线性影响，但该类前馈补偿策略是根据系统理论输入值来实现前馈补偿的，对误差响应较为迟钝，不具有很好的自适应能力。罗青竹等在MFC系统中提出了前馈模糊逻辑PID 算法[10]，虽然解决了非线性问题，优化PID参数，提高了抗干扰能力，但模糊逻辑的初始逻辑很难把握，应用在直流伺服系统中依然无法满足起始的动态响应问题。鉴于以上考虑，本文以滑行灯随动转向系统为研究对象，建立了基于计算速度误差的摩擦模型前馈补偿算法结合模糊PID控制，提出的理论根据是在低速转动系统当中导致转速偏差的主要因素是摩擦阻尼效应，建立对应摩擦模型，将误差值实时地以电流-转矩的形式前馈补偿给系统，目标在于消除主要非稳定因素，实现更加精确快速的灯具动态响应。有效弥补后者在参数整定中因适应能力不足而出现的不稳定现象。

该系统主要包括三大模块：数据采集、中央智能控制和执行模块。其中智能控制模块通过预定程序将从信息采集模块接收到的相关信息进行分析计算，然后向执行模块发出指令驱动执行机构完成系统工作。

2 建立转角模型

要实现灯具的随动转向，首先应建立其转角模型，可根据滑行速度和前轮转角等输入信号确定理论转角。这里为了方便计算，将飞机主起落架上的若干主轮等效为后左右轮，从而建立起三轮转弯模型如图1(a)。

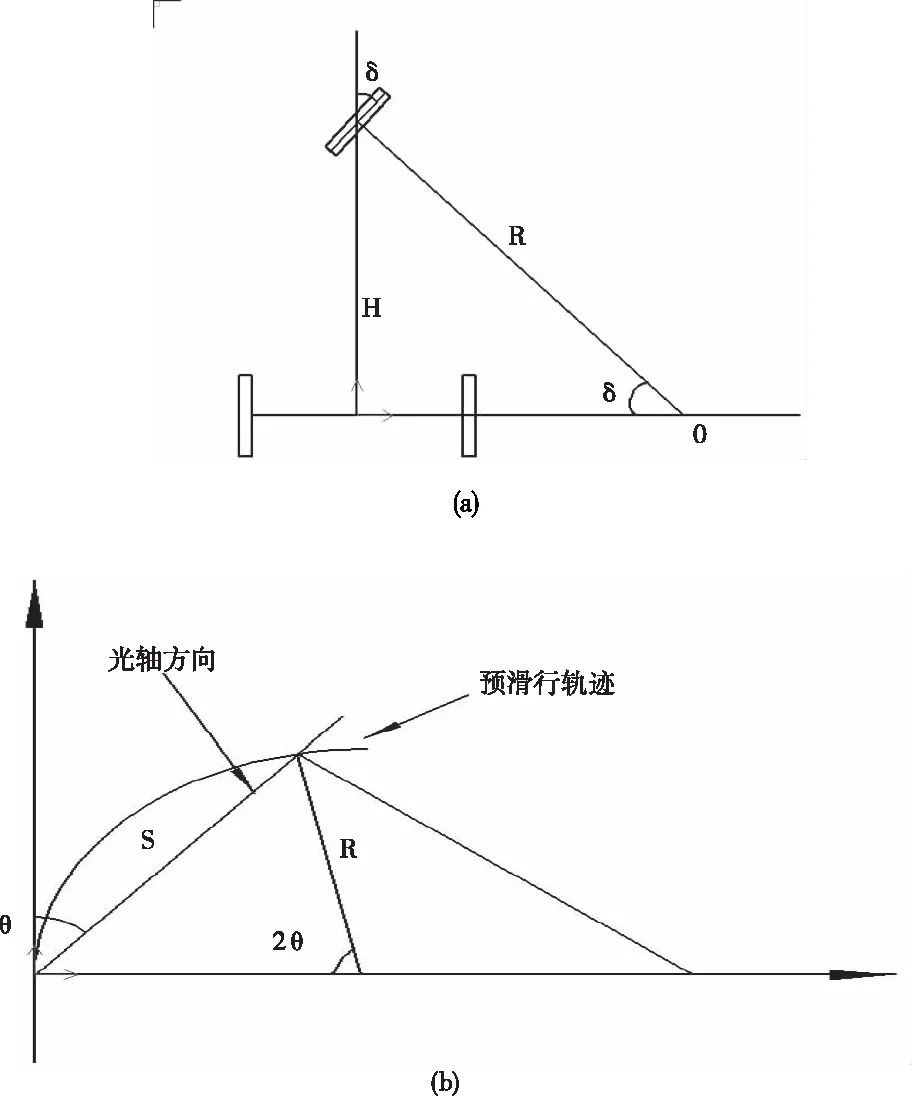
图1 转角原理示意图

参照阿克曼转向原理[11]，以前后轮的轴线延长线交点为圆心，仅以前轮轨迹线切圆半径为飞机的瞬时转弯半径R，前轮转角为飞机行驶转角δ。适航标准对滑行灯转弯时照度没有明确要，可根据其直线滑行标准规定灯具最大转向角为±15°由图1(a)几何关系有

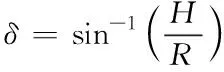
(1)

并通过理论制动距离建立滑行速度与灯具转角之间的关系。光轴沿预设滑行轨迹的割线方向，称S为停机视距。 由图1(b)的几何关系得：S=2RsinS=2Rsinθ。所以

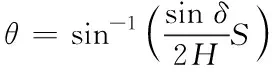
(2)

(H为飞机主、前轮轴距，取31.88m，δ为前轮转角，θ为灯具转角)。

停机视距S=S1+S2+S3.根据相关资料，A380主机轮承载整机90%的重量，沥青道面摩擦系数μ为0.8。

由

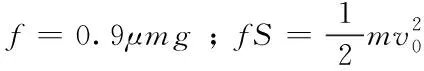
(3)

得

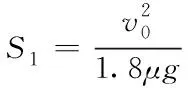
(4)

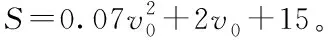
则

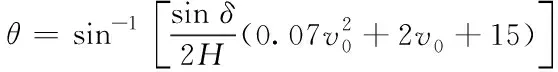
(5)

三维图像见图2。

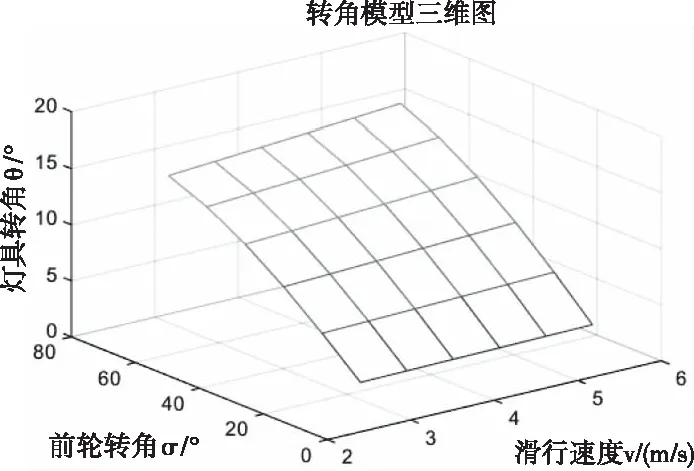
图2 灯具三维转角模型

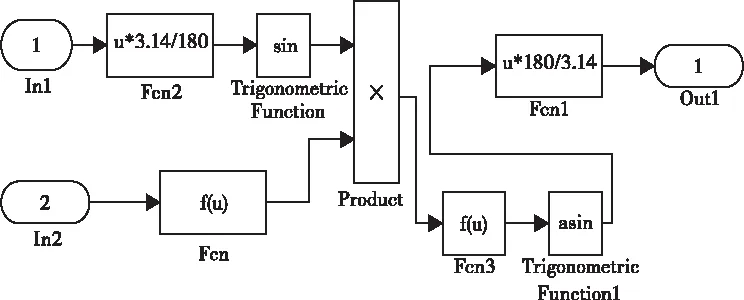
图3 滑行灯转角仿真模型

系统结构如图4所示。

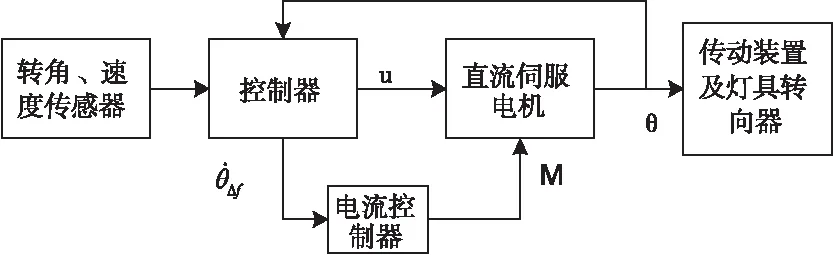
图4 系统结构简图

3 电机模型

被控对象主要是伺服电机以及带有减速机构的负载模型。具体通过改变输入电压u控制输出角速度ω，再经过减速器输出目标转角θ。直流伺服电机具有转速范围广、堵转转矩大、不受频率与极对数的限制、机械特性及调节特性的线性度高、功率损耗小等优点。本文选用直流伺服电机FAULHABER2342L012CR参数[12]。

其开环传递函数为

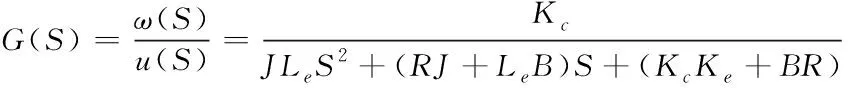
(6)

式中：u——输入电压值；ω——输出轴(灯具)转速；S——拉氏算子。

4 摩擦模型

作为影响机械系统动态响应的主要因素之一，已被提出的摩擦模型主要有Karnopp 模型、Dahl模型、Lu Gre模型及 Stribeck模型[13]。经典摩擦模型中摩擦力是速度的线性函数，针对本系统的低速伺服特性，本文选用Stribeck摩擦模型，在客服了静摩擦力后并不随着速度的增加而线性增加，在一定的速度范围内有连续下降的现象，称为负斜率摩擦现象，在此基础上再添加黏性摩擦项，Stribeck摩擦模型可表示如下：

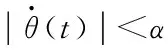
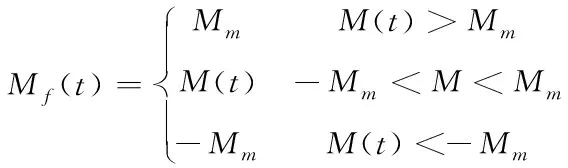
(7)

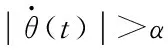
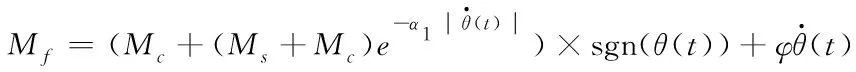
(8)

其中Ms为最大静摩擦力，Mc为库伦摩擦力φ为黏性系数，α和α1都为很小的常量

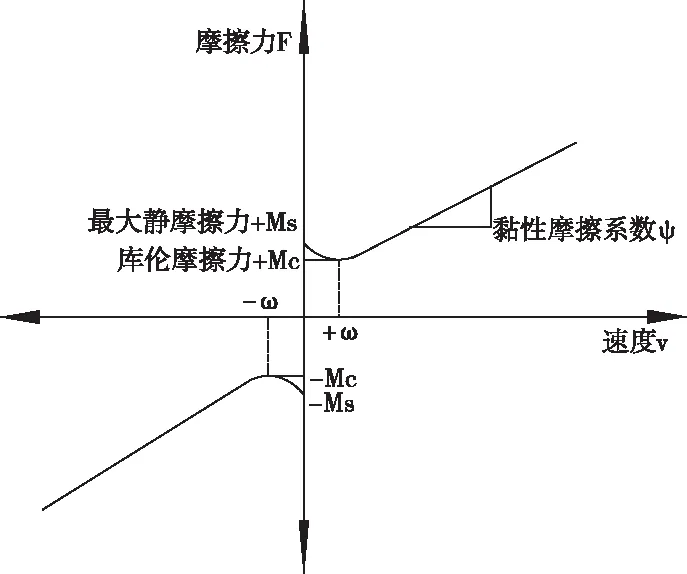
图5 摩擦模型

又

Δu=ue-ub；

(9)

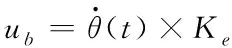
(10)

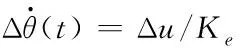
(11)

(等效建立)

综合式(8-11)得

MΔf=(Mc+(Ms+Mc)e-α1|Δu/Ke|)×

sgn(Δu/Ke)+φΔu/Ke

(12)

其中MΔf为前馈补偿力矩；Δu为电动势差；控制电流和力矩呈线性关系

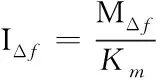
(13)

摩擦模型中的参数是通过动力学仿真系统辨识以及结合经验所得，本文所取参数见表1，摩擦模型框图见图6。

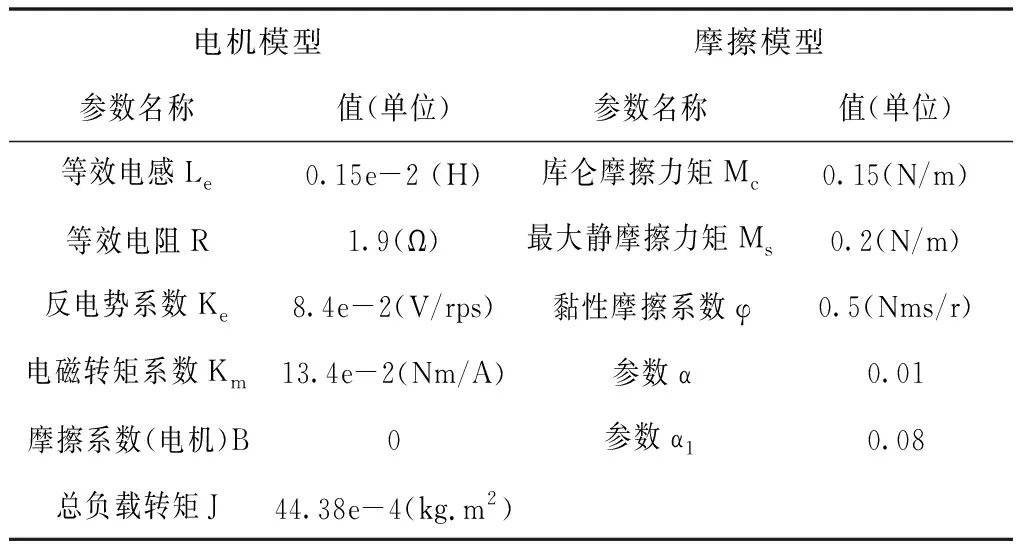
表1 电机-摩擦模型参数

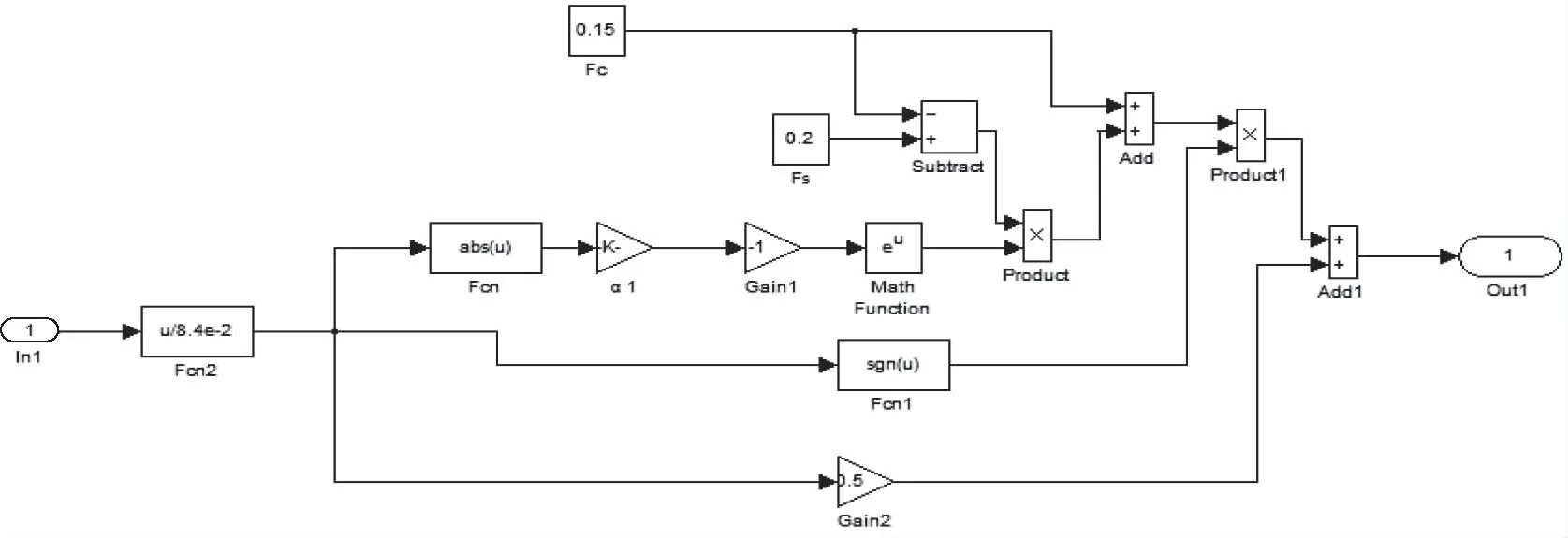
图6 Simulink-摩擦模型

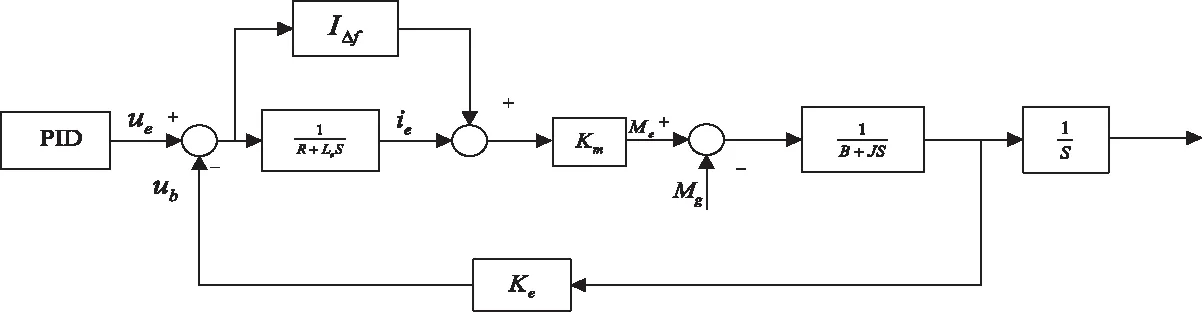
图7 加摩擦前馈补偿的简化电机模型

5 模糊PID控制器

PID控制应用于液位、温控等具有非线性、时变性、时滞性的系统当中，其原理是将设定目标或理论值和反馈值之间的偏差的比例P、积分I、微分D结果通过线性组合生成控制量对系统进行控制[14]。 本系统的研究涉及到多输入和诸多不稳定因素的影响，而PID控制的优劣决定于比例、微分和积分三个参数的设定，确定的参数在控制过程中无法更好地适应该类系统[15]。 因此，采用模糊理论实现PID参数的在线自整定，来改善动态响应特性[16-17]。

5.1 PID控制算法

常规的PID控制算法

(14)

其中：e(t)为偏差值，Kp为比例系数，TI为积分时间常数，Td为微分时间常数。 为了便于计算机的实现，将积分和微分部分改为求和与求差的形式：

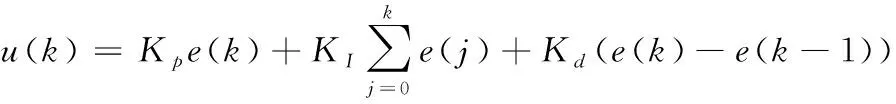
(15)

其中的k指采样点的个数，Kp、KI、Kd分别表示比例、积分和微分常数。

5.2 模糊自整定原理

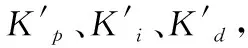
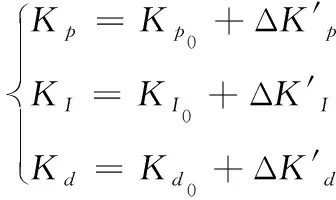
(15)

所以，该模糊控制器所调整的是PID三个控制参数的变化量，而Kp0、KI0、Kd0、通过传统的临界比例度法获得的。

5.3 模糊PID控制器设计

5.3.1 选择变量及模糊化

根据本系统的要求采用两输入三输出的形式，输入变量：偏差e和偏差变化率ec取量化论域分别为[-3，3]和[-1，1]，都取七个模糊子集，语言变量为{NB，NM，NS，ZO，PS，PM，PB}，输出变量：ΔKp、ΔKI、ΔKd取量化论域都为[-1，1]，取五个模糊子集{NB，NS，ZO，PS，PB}。 在MATLAB中的Fuzzy工具箱中定义以上论域及语言变量，并选用灵敏度较高、分布相对均匀的三角形函数作为隶属度函数。

5.3.2 建立模糊规则

根据实际生产和工作经验，PID控制参数在各种工况下的自整定一般符合以下规则[18]。

1) 当|e|较大时，无论偏差变化率大小，为了提高系统的快速响应性能，应取较大的Kp和较小的Kd，同时为了尽量减小系统的超调量，应限制积分作用，取较小的KI值。

2) 当|e|中等大小时，为使系统响应在具有较小超调的同时保证系统的响应速度，应取较小Kp，而KI和Kd大小要适中。 其中Kd的取值对系统响应的影响较大。

3) 当|e|较小时，为保证系统具有较好的稳态性能，Kp和KI应取的大些，同时为了提高系统的抗干扰能力，当ec较小时，Kd取大些； 当ec较大时，Kd应取小些。

通过分析和参考专家经验，得出模糊控制规则表，见表2。

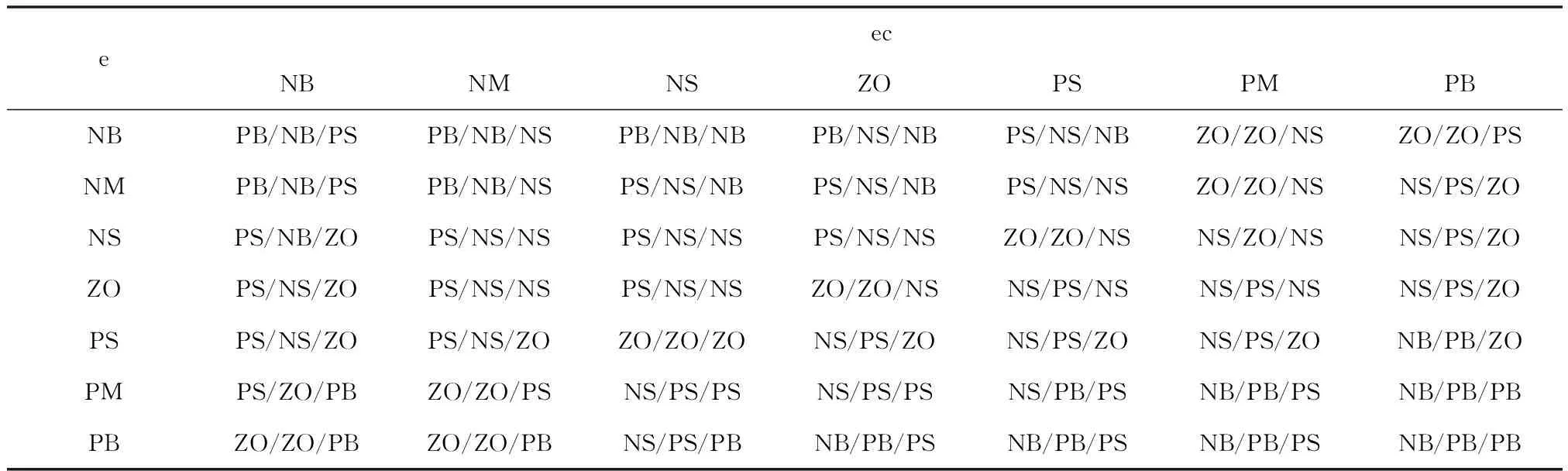
表2 ΔKp/ΔKI/ΔKd控制规则调整表

以上规则可以If……then……的形式表达，如：

Ruler：If (e is NB) and (ec is NB) then (△Kp is PB) and (△KI is NB) and (△Kd is PS)；……

然后将所有模糊变量及模糊规则输入至MATLAB中的Fuzzy工具箱，建立模拟模糊控制器如图8、图9所示，选centroid解模糊法。

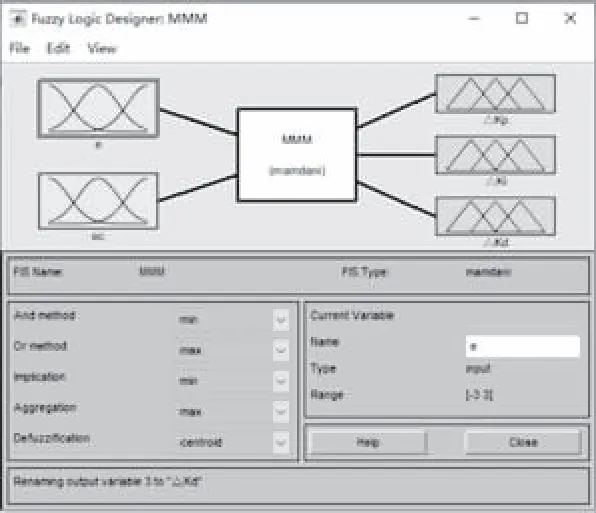
图8 模糊逻辑设计图

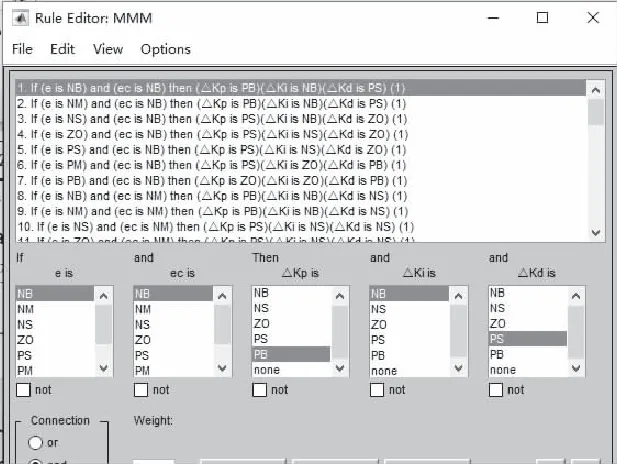
图9 模糊规则的确立

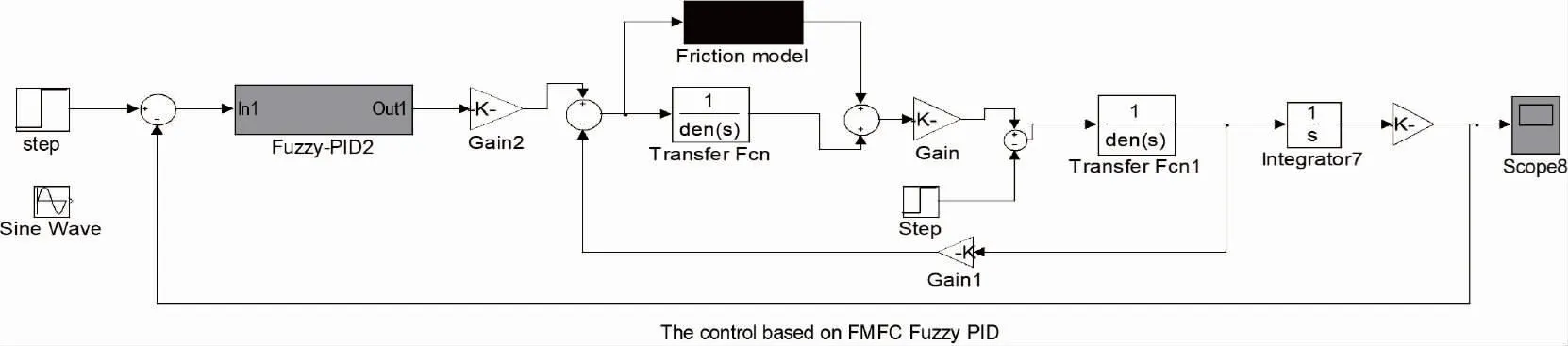
图10 转矩前馈补偿模型模糊PID控制

6 系统仿真

利用Simulink模块进行系统仿真[18]，利用试凑法取量化因子：Ke=0.5，Kec=0.02，比例因子：Up=200，UI=1，Ud=0.1，通过传统Z-N整定法获得PID参数的初始值：Kp0=200、KI0=0.01、Kd0=2以下仿真将从两个方面作出验证。

6.1 阶跃输入下的动态特性

当控制端发出转向命令时，灯具需要作出快速稳定的响应，设定阶跃输入幅值为1°，仿真时间为2s，步长0.01s。 图13为系统仿真框图，对比五种不同控制方案(PID控制、模糊PID控制，摩擦模型前馈补偿控制、摩擦模型前馈补偿PID控制、摩擦模型前馈补偿模糊PID控制)下的动态特性曲线，如图12所示，测量结果见表3所示。

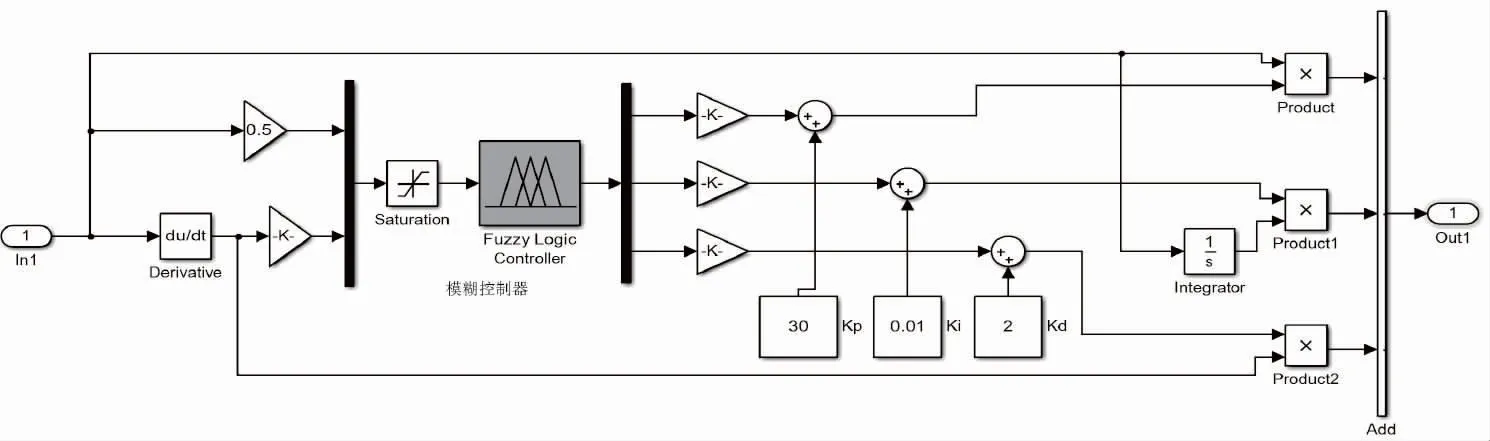
图11 模糊PID控制器

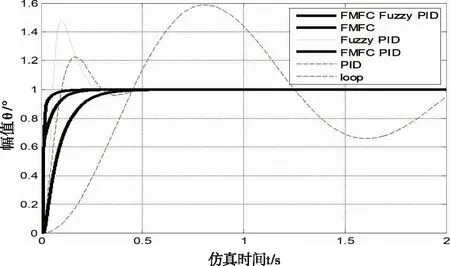
图12 正弦输入响应曲线(注：FMFC：Friction model feedforward control)

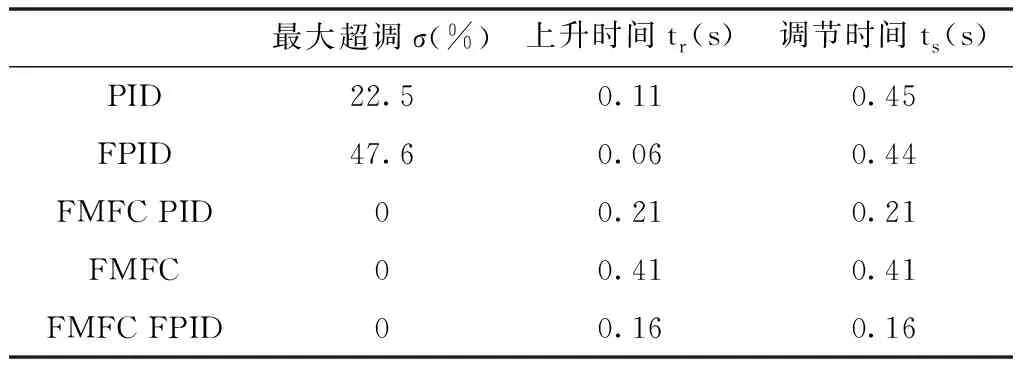
表3 动态特性曲线指标对比

由仿真结果可以看出：加入了摩擦模型前馈补偿后的动态响应曲线各指标明显优于单纯的PID控制和模糊PID控制，经前馈补偿后的模糊PID控制具有更加稳定快速的响应特性。

为了测试以上控制策略的抗干扰能力，于仿真时间1.3s处加入一扰动转矩：-0.15Nm，观察结果见图13、14。

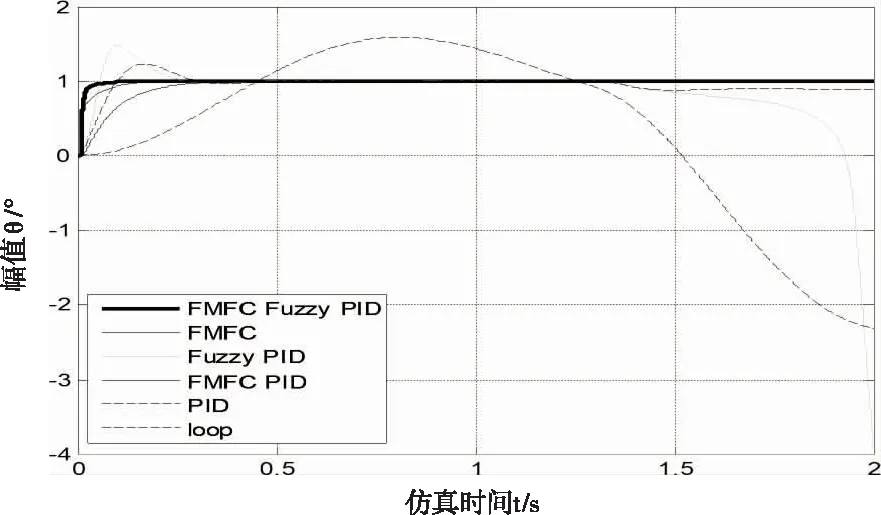
图13 扰动响应曲线

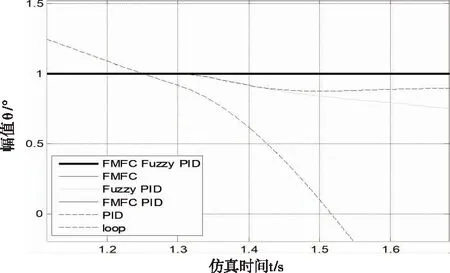
图14 局部响应曲线

加入扰动后发现PID和模糊PID控制出现了较大的偏差，甚至后者还出现了较大的振荡现象，这在实际工作中是非常危险的，而加入摩擦模型补偿的其它三种控制策略都表现出了很好的稳定性。

6.2 正弦输入下的动态特性

除了验证瞬态响应和抗干扰能力还需要被控系统具有不错的跟随性能，当输入为幅值为1°，频率为2r/s的正弦信号时，见图15、16：由误差变化曲线可以看出仅有摩擦前馈补偿的闭环控制误差大于±0.1°，单纯的PID和模糊PID控制在经受扰动后都出现了比较大的偏差，只有基于摩擦前馈补偿的PID和模糊PID控制总维持在±0.02°范围内，体现出不错的跟随能力，经上述综合对比，基于摩擦模型前馈补偿的模糊PID控制具有最优的动态响应性能。

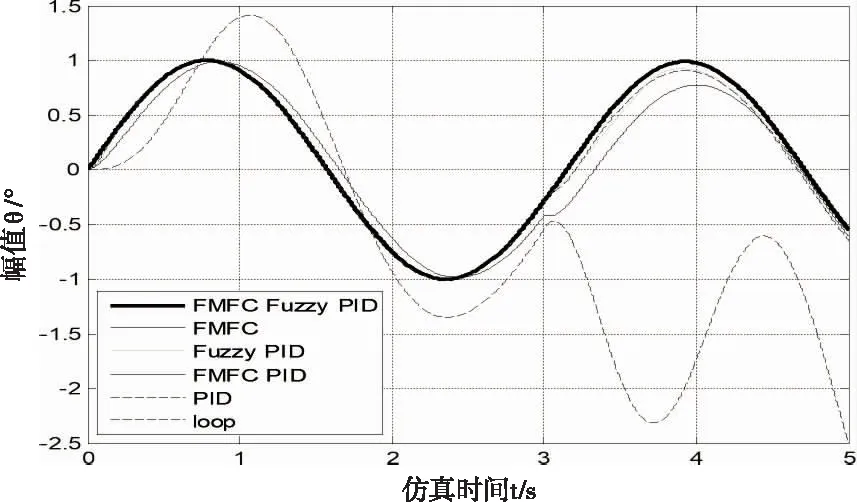
图15 正弦响应曲线

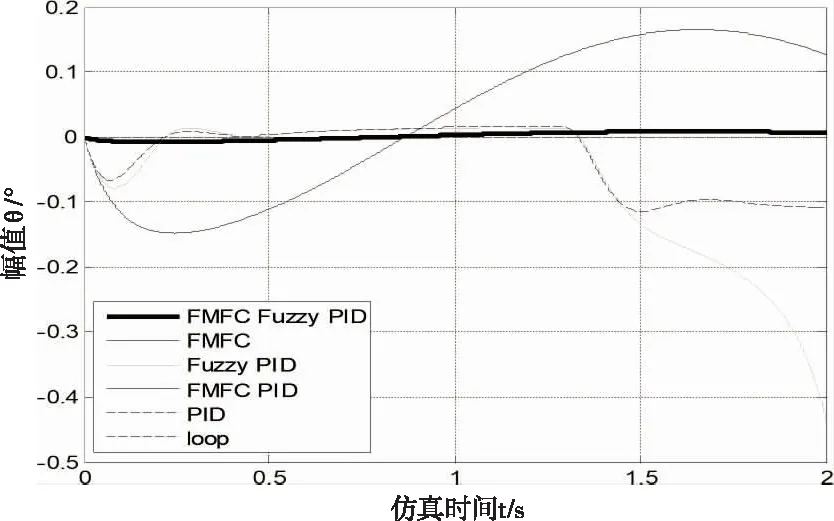
图16 跟随误差曲线

7 结束语

该滑行灯随动转向系统采用了三轮转向模型，根据前轮转角和滑行速度两个输入变量结合飞机地面滑行理论制动距离建立起灯具转角模型。以直流伺服电机作为执行机构，将负载模型与电机模型合并建立等效电机模型，将影响系统响应的主要因素摩擦现象提出来，建立Stribeck摩擦模型，通过压差——速度误差值计算摩擦转矩实现控制电流的前馈补偿。然后利用MATLB/Simulink建立系统仿真模型，比较了PID控制、模糊PID控制，摩擦模型前馈补偿控制、摩擦模型前馈补偿PID控制、摩擦模型前馈补偿模糊PID控制五种控制方案，结果表明基于摩擦模型前馈补偿的模糊PID控制具有响应速度快、超调量小、跟随性能和鲁棒性强等特性，适用于该控制系统。