非恒定流作用下的阶梯形丁坝局部冲刷特性

钟 亮，姜 利，姜 彤，李国际，陈镜元

(1.重庆交通大学 国家内河航道整治工程技术研究中心，重庆 400074； 2.重庆交通大学 河海学院，重庆 400074)

1 研究背景

丁坝是常见的航道整治建筑物，具有束水攻沙和改善流态等作用。航道整治中，丁坝纵剖面多采用单一断面型式(简称“单式断面丁坝”)；但对某些汛期泥沙淤积严重、退水期冲刷不及的碍航浅滩河段，为增加航槽冲刷和减小防洪影响，丁坝纵剖面常采用2级整治水位相结合的型式，并设计成阶梯形(简称“阶梯形丁坝”)[1]，目前阶梯形丁坝在航道整治中应用广泛[2-3]。

丁坝周围的冲刷可分为局部冲刷和普通冲刷，其中局部冲刷是坝体水毁的主要原因[4]，因而受到广泛关注。单式断面丁坝方面，潘军峰等[5]、Bey等[6]、Zhang等[7]、Kuhnle等[8]采用水槽试验和数值模拟等方法，分析了丁坝周围的水流结构特征，认为丁坝周围形成的马蹄涡、尾涡和下潜流等水流结构，是造成局部冲刷的主要原因；彭静等[9]根据最大冲深将冲刷过程分为初始阶段、发展阶段和平衡阶段，其中初始阶段的丁坝局部冲刷最为明显；Pandey等[10]、张立等[11]的丁坝清水冲刷试验研究显示，最大冲深与上游来流强度、冲坑平面展宽速率和泥沙粒径等有关；宁健等[12]应用水流泥沙数学模型，探讨了河宽束窄率对最大冲深的影响；喻涛等[13]基于概化水槽试验，研究了非恒定流作用下的丁坝局部冲刷问题，发现随着坝后冲坑下游沙垄的形成与消亡，冲坑范围会出现短时减小的现象。阶梯形丁坝方面，钟亮等[1,14]基于水槽试验和数值模拟等方法，探讨了阶梯形丁坝的水流流速分布特征及下游回流规律，为冲刷特性研究奠定了基础；丁晶晶等[15]探讨了台阶尺度、级数等对台阶式丁坝局部冲坑的影响。

综上所述，国内外丁坝局部冲刷问题研究主要针对单式断面丁坝，且多为恒定流条件，非恒定流作用下的阶梯形丁坝局部冲刷特性问题研究还较薄弱，相关认识仍需加强。为此，本文以阶梯形丁坝为例，通过自回归马尔柯夫模型概化天然非恒定来流过程，基于平面二维水流泥沙数学模型，探讨非恒定流作用下的阶梯形丁坝局部冲刷特性。

2 数值模拟

2.1 模型控制方程

采用平面二维水流泥沙数学模型进行研究，模型控制方程和相关计算公式如式(1)—式(6)所示。

水流连续方程为

(1)

水流运动方程为

(2)

(3)

泥沙输运模型主要采用Engelund-Hansen输沙理论，总输沙率Stl表示为

(4)

泥沙连续方程为

(5)

河床变形方程为

(6)

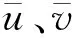
2.2 模型率定与验证

采用喻涛[16]的水槽试验资料进行模型率定与验证，试验流量为非恒定流，试验水槽为矩形玻璃水槽，长30 m、宽2 m、高1 m，水槽中部铺设了长8 m的动床段，丁坝周围槽底铺沙厚22 cm，其余区域铺沙厚10 cm，床沙粒径d50=1.0 mm，重度γs=26.5 kN/m3；丁坝位于水槽左岸，距进口12.75 m，丁坝高10 cm、底长75 cm、底宽42.5 cm，迎水坡坡比1∶1.5、背水坡坡比1∶2、坝头坡比1∶2.5，坝头为圆弧形直头。

计算区域采用三角形网格进行剖分，网格边长约8 cm，丁坝区域网格进行了局部加密处理，边长约2 cm，求解格式精度采用一阶精度方法。在水流运动模块中，设定水槽左右两岸均为陆边界，水流的法向分量恒为0，Vn(x,y,z,t)=0，无热、盐交换，不考虑风、柯氏力影响；主时间步长与最大时间步长取值为0.2 s，最小时间步长取值为0.001 s，临界克朗数取为0.8；不考虑密度梯度流，选择Barotropic正压模型，即温度和盐度为常数，密度则保持不变；设定湿水深hwet=0.05 m，干水深hdry=0.005 m，淹没水深hflood=0.05 m；水平涡粘系数采用Smagorinsky公式，Cs取为0.28；曼宁系数为70，即设定糙率n为0.014 3。在泥沙输移模块中，设定泥沙输移仅受单一水流条件作用，进口与出口边界均为0梯度，即无泥沙输入与输出。

2.2.1 水位验证

选取最大洪峰流量时的水位进行验证，限于篇幅，这里仅给出左岸、中轴和右岸3条纵向水面线的验证结果(图1)，对比显示，计算值与实测值的符合程度较高，水面线走势吻合较好，水位偏差基本在0.1 cm以内。

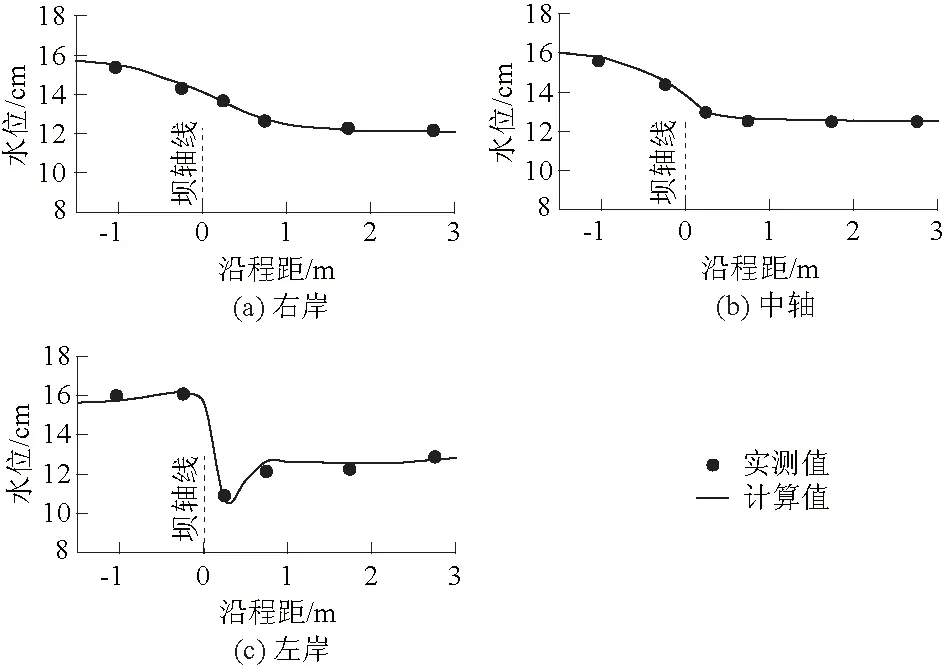
图1 水位验证Fig.1 Verification of water level

2.2.2 流速验证

图2给出了纵向时均流速的验证结果，图中实测值为最大洪峰流量时的流速；以坝轴线(CS2)为基准，上游测流断面CS1距坝轴线26.25 cm，下游测流断面CS3、CS4分别距坝轴线73.75 cm和173.75 cm。验证表明，计算流速与实测流速在大小、分布上均较吻合，流速偏差基本在0.05 m/s以内。

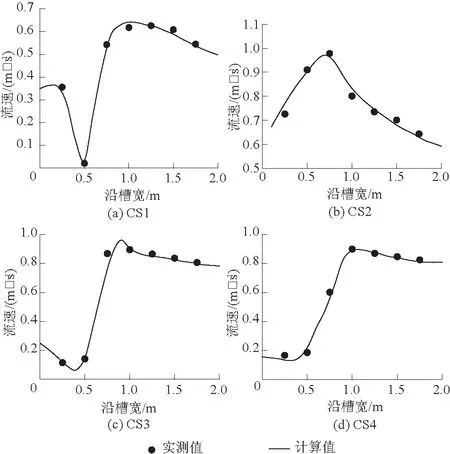
图2 流速验证Fig.2 Verification of flow velocity

2.2.3 冲淤变形验证

图3给出了典型断面的河床冲淤变形验证，图中冲淤深度正值表示淤积，负值表示冲刷，零值表示不冲不淤；断面CS1位于丁坝上游26 cm，断面CS2、CS3、CS4分别位于丁坝下游26、76、176 cm。结果显示，计算和实测的泥沙冲淤部位基本一致，冲淤偏差基本在0.5 cm以内，符合程度良好。

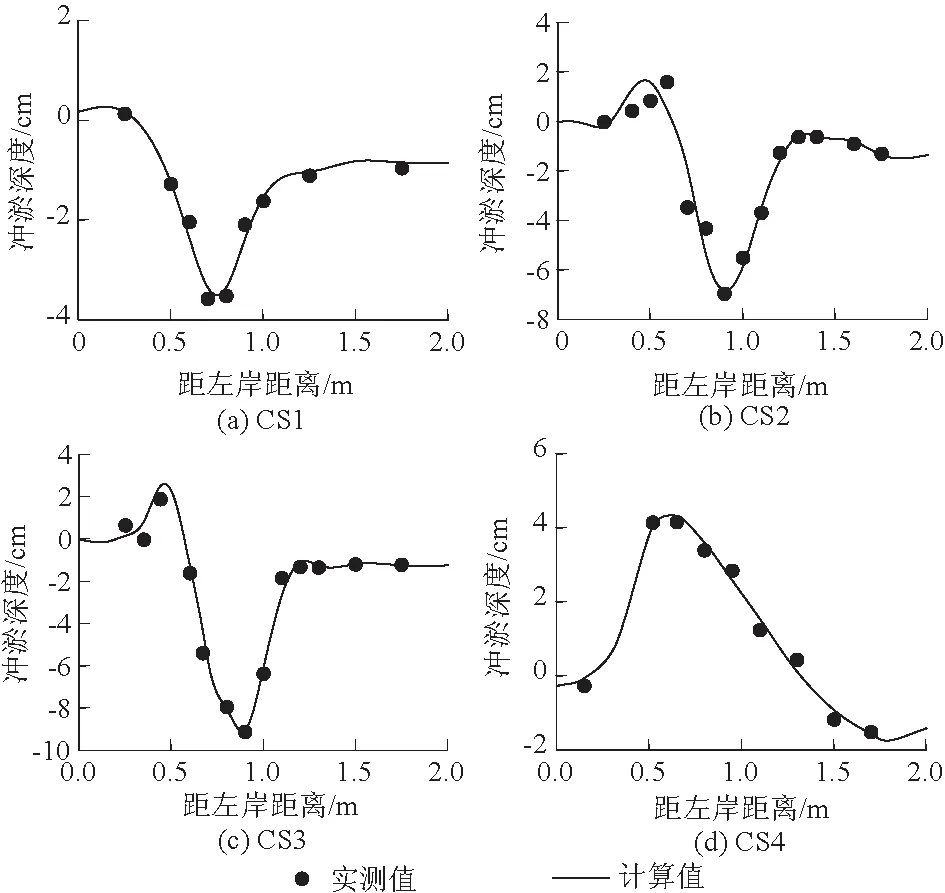
图3 冲淤变形验证Fig.3 Verification of erosion and deposition deformation

综上所述，水位、流速、河床冲淤变形的计算值与实测值吻合良好，本文模型可用于后续研究。

2.3 计算条件

参考《航道工程设计规范》(JTS 181—2016)，并考虑水槽和丁坝对水流泥沙运动的影响，数值模拟时，采用正挑阶梯形丁坝，迎水坡坡比为1∶1.5，背水坡坡比为1∶1.5，坝头坡比为1∶1，坝头采用圆弧形直头。

本文研究主要针对非淹没丁坝，丁坝总高H=0.1 m，坝顶宽b=0.1 m，一级坝高Hd1=0.05 m，一级坝长Ld1=0.8 m，二级坝长Ld2=0.55 m，床沙中值粒径d50=0.8 mm，丁坝尺度及网格划分见图4。为与恒定流条件下的局部冲刷特性进行对比，设置了1组恒定流计算工况，流量Q=80 L/s，尾门断面水深h=0.08 m，丁坝纵剖面、床沙条件均与非恒定流条件保持一致。研究表明[9,17]，该恒定流条件下冲刷6 h床面冲刷即可达到平衡。数值模拟时，其余参数设置均与模型率定与验证时保持一致。

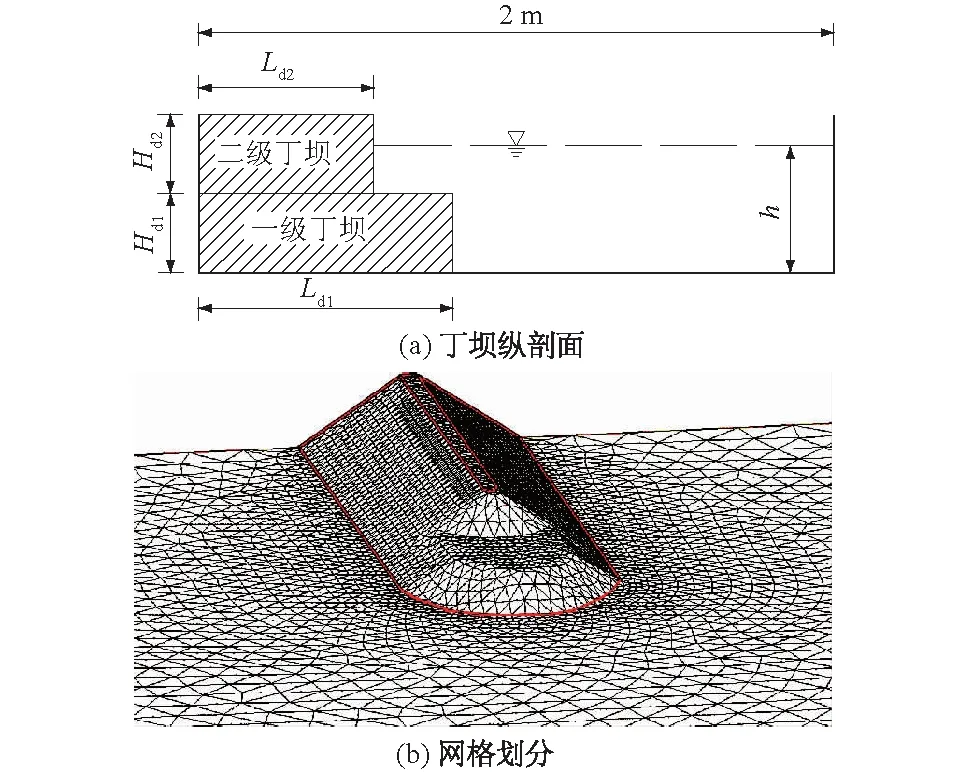
图4 丁坝纵剖面及网格划分Fig.4 Longitudinal profile and grid division of spur dike

为模拟天然河流的典型非恒定来流过程，选用长江上游寸滩水文站1955—2012年的实测日均流量资料，并统计获得年径流序列过程；然后根据Mann-Kendall突变检验法，确定年径流序列中的14个突变点，并将其剔除；最后采用自回归马尔柯夫模型[13]，结合正弦变化流量特征曲线，得到相应的模拟流量过程[17]见图5(a)。为使非恒定来流总量与恒定来流时保持一致，将得到的模拟流量过程，按比例重新分配到平均流量为80 L/s、周期为6 h的流量过程内，该时段内的总来水量为1 728 m3；尾水位则采用明渠均匀流公式计算得到。数值模拟采用了周期相同、起始流量不同的2种概化来流过程，即波谷起冲与波峰起冲，见图5(b)；随冲刷历时的增加，波谷起冲来流过程依次经历涨水期和落水期，波峰起冲来流过程依次经历落水期和涨水期。

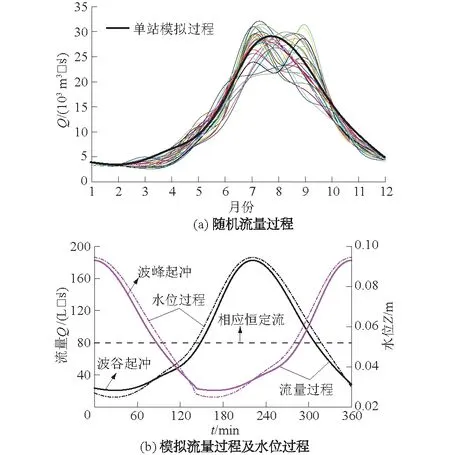
图5 典型来流过程概化Fig.5 Generalization of typical inflow process

3 结果分析

3.1 丁坝区流速分布特性

图6给出波谷起冲和波峰起冲条件下不同时刻的丁坝区平面流场分布，其中水流正向由左至右，流速为0的区域为床面淤积处。与恒定流时相似，受丁坝阻水和挑流等作用的影响，非恒定流作用下的丁坝水流可分为主流区、上游滞流区和下游回流区[18]。

图6 平面流场分布Fig.6 Distribution of plane flow field

波谷起冲来流过程下，在涨水期(t≤3.75 h)，随着上游来流量的逐渐增大，水流靠近丁坝时产生绕流，使得坝头局部流速增大，坝后主流区流速增大，主流高速区逐渐向丁坝岸侧、丁坝断面处移动；受水槽左边界的影响，偏移的主流区使下游回流区的范围被逐渐压缩，回流长度与宽度逐渐减小，回流区流速逐渐增大。在落水期(t>3.75 h)，随着上游来流量的逐渐减小，主流区流速也随之减小，下游床面落淤逐渐出现，且淤积量逐渐增多；受淤积区的影响，主流区被逐渐分离成2个区域，回流区的长度与宽度缓慢减小，回流区流速也逐渐减小。

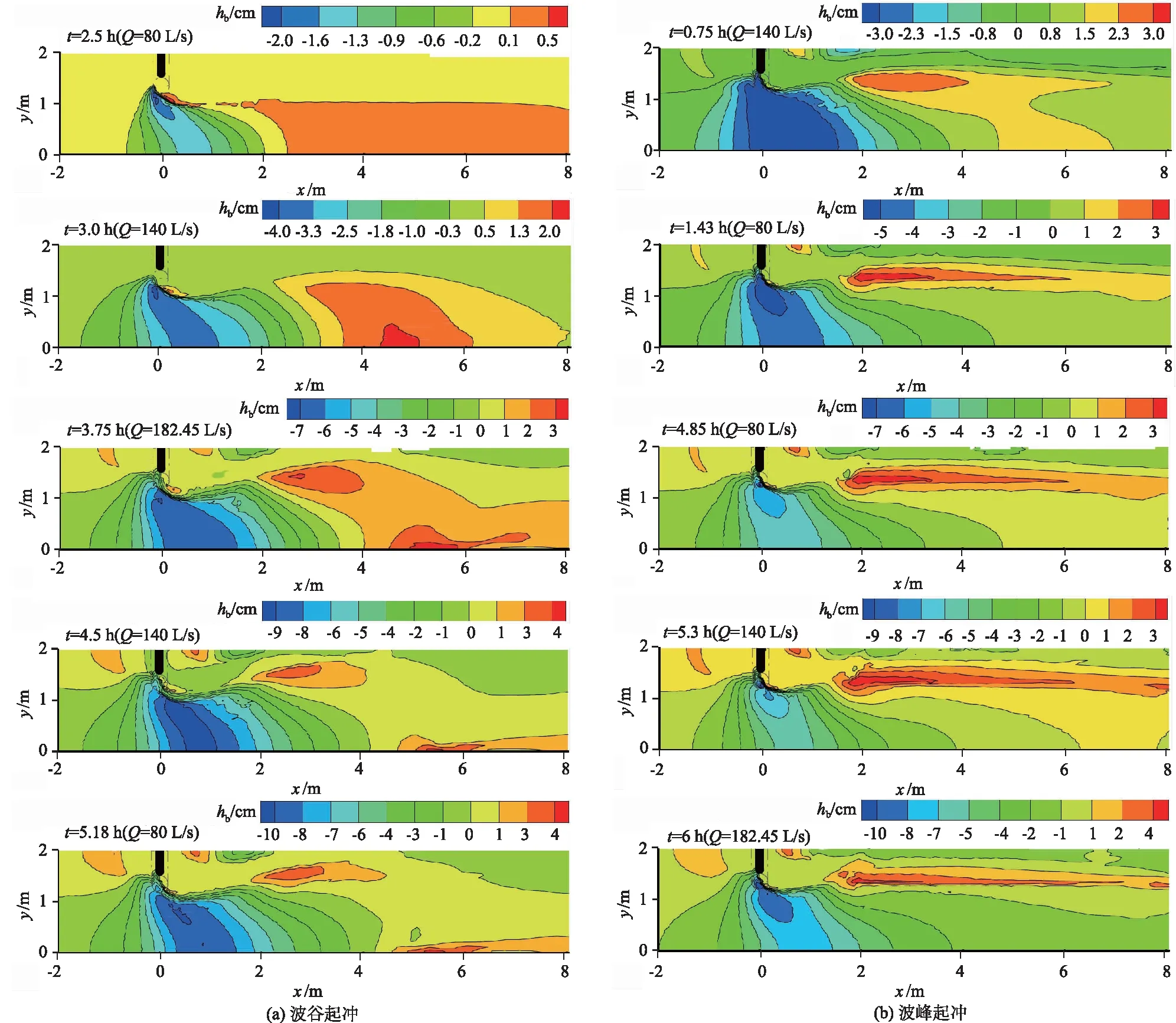
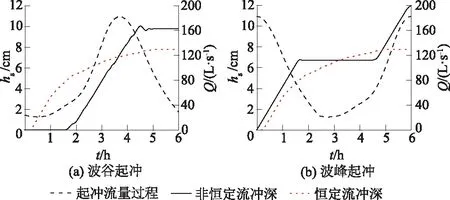
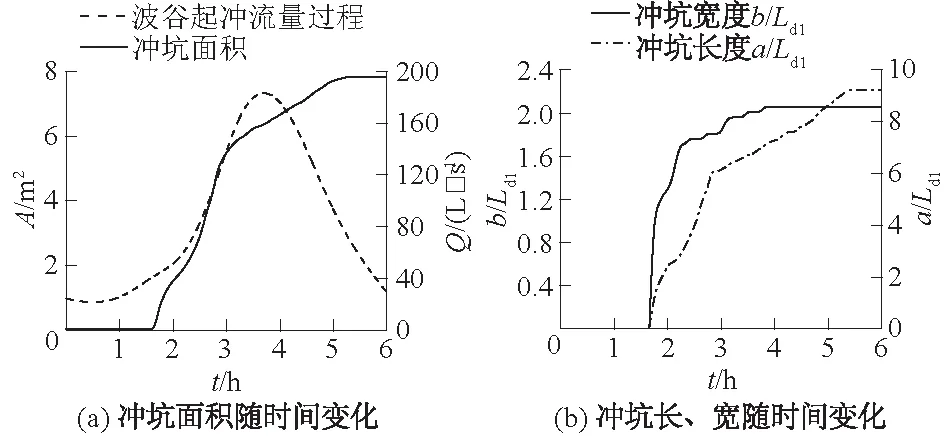
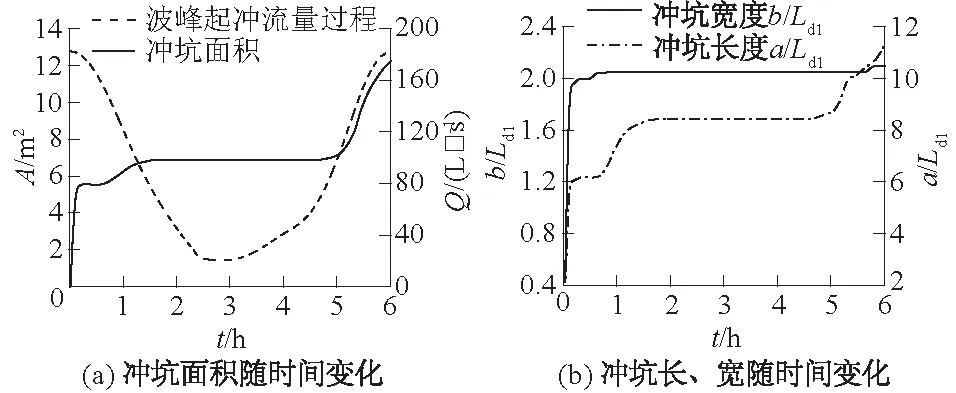
波峰起冲来流过程下，在落水期前期(t≤1.43 h)，由于初始流量为最大流量，下游河床开始产生了较大的冲淤变形，随着上游来流量的逐渐减小，背离丁坝岸侧的主流区流速也随之减小，下游床面淤积逐渐增多；受淤积区和水槽左边界的影响，主流区开始被分离成2个区域，其中靠近丁坝岸侧的主流区流速逐渐增大，回流区的长度、宽度和流速逐渐减小。在落水期后期和涨水期前期(1.43 h

总体而言，6 h冲刷历时中，当上游来流量相同时，波谷起冲条件下，涨水期的主流区流速、回流区尺度均较落水期大，但落水期的下游床面淤积较涨水期明显；波峰起冲条件下，受下游淤积区及水槽左边界的影响，小流量时的涨水期主流区流速、回流区尺度较落水期无明显变化，大流量时的涨水期主流区流速、回流区尺度较落水期小，但其中靠近丁坝岸侧的部分主流区流速较落水期大。

3.2 坝头冲坑发展过程

3.2.1 冲坑形态发展过程

图7给出了波谷起冲和波峰起冲时的床面冲淤形态变化,图中hb表示床面冲淤高度。波谷起冲来流过程下，涨水期(t≤3.75 h)，坝头附近的冲刷随上游来流量的增加迅速发展，冲刷深度逐渐增大，冲坑沿横向和纵向均明显延长，上游边界逐渐由上凸形发展为下凹形；坝后主流高速区向丁坝侧移动，回流区宽度减小、流速增大，使得靠近坝头的冲坑下游边界逐渐向强冲深区收缩；与此同时，较高流速水流的持续冲刷，使冲坑后方淤积区有被分成2个区域的趋势。落水期(t>3.75 h)，随上游来流量的逐渐减小，冲坑下游边界沿纵向继续延长，而上游边界变化极小；由于落水期前期的上游来流量较大，受主流区较高流速水流的持续冲刷，冲坑后方淤积区被冲刷成了2个区域；受下游淤积区的阻水影响，冲坑下游边界向下游凸出后回缩，接近回流区的冲坑下边界逐渐变得平缓。

图7 床面冲淤形态Fig.7 Erosion and deposition patterns of bed surface

波峰起冲来流过程下，落水期前期(t≤1.43 h)，冲坑上、下游边界沿横向和纵向的变化与波谷起冲落水期的冲坑边界发展相似，但由于2种条件下的坝后淤积区位置不同，下游边界向下游凸起后未回缩；受初始流量大小的影响，波峰起冲条件下的下游河床，开始便出现了较大的冲淤变形，而坝后淤积区受主流区较高流速水流的挤压，逐渐在靠近丁坝岸侧处，形成一条狭长的淤积带；受淤积带的阻流作用，靠近淤积区的冲坑下游边界逐渐向强冲深区收缩。在落水期后期与涨水期前期(1.43 h

3.2.2 坝头最大冲深发展过程

图8给出了最大冲深hs随冲刷历时的变化。波谷起冲来流过程下，冲刷大约在t=1.75 h(涨水期Q=43.2 L/s)时开始，随着上游来流量的增大，冲坑迅速发展，冲深随时间呈线性增长；达到最大流量后，由于主流区流速较大，冲刷仍将高速发展，直到t=4.5 h(落水期Q=140.0 L/s)时，冲深才达到最大值；随着主流区流速的逐渐减小，水流冲刷能力显著减弱，此时冲坑边壁由于不稳定而坍塌，冲深有所减小，到t=4.92 h(落水期Q=100.6 L/s)时，最大冲深趋于稳定。

图8 最大冲深随冲刷历时的变化Fig.8 Variation of maximum scour depth withscouring duration

波峰起冲来流过程下，由于初始流量为最大流量，冲刷在t=0 h时便开始，冲深随着时间呈线性增长；当t=1.75 h(落水期Q=60.1 L/s)时，冲刷发展到一定的深度，由于落水期过渡到涨水期的一段时间内，上游来流量始终较小，此时的水流挟沙能力较弱，局部冲刷不再发展，冲深保持在一个稳定值；直到t=4.58 h(涨水期Q=62.8 L/s)时，流速增至可继续冲刷，冲深随时间再次呈线性增长，增长速率与t≤1.75 h(落水期)时基本一致。

与恒定流条件对比，恒定流的冲深发展速率随冲刷历时逐渐降低，非恒定流的冲深发展速率随冲刷历时几乎不变。6 h冲刷历时中，恒定流条件下的最大冲深可达7.77 cm；非恒定流波谷起冲、波峰起冲条件下的最大冲深分别可达9.75 cm和11.99 cm(t=6 h)，较恒定流时增加25.5%～54.3%。

3.3 冲坑平面尺度的发展规律

3.3.1 波谷起冲条件下的发展规律

图9给出了波谷起冲条件下的冲坑尺度随时间变化，其中A为冲坑面积，a/Ld1、b/Ld1分别为无量纲化后的冲坑长度和冲坑宽度。

图9 波谷起冲条件下的冲坑尺度随时间变化Fig.9 Scale variation of scour pit with time underthe condition of trough inflow process

对于冲坑面积随时间变化，坝头局部冲刷开始后(t=1.75)，随上游行近流速的逐渐增大，主流高速区向丁坝岸侧偏移，使冲刷坑面积在涨水期迅速增长；因非恒定流的流量、流速等各水力参数之间存在着不同步的现象，当流速达到最大时，流量还未达到最大[16]，因而在最大流量到达前，冲坑面积增长速率开始变缓；落水期的冲坑面积增长也基本保持着这一增率，直到t=5.3 h(落水期Q=67.9 L/s)，冲坑面积才达到稳定。

对于冲坑长度和宽度随时间变化，冲坑长度随冲刷历时的增长速率与冲坑面积基本一致，涨水期增长速率较快；在t=2.83 h(涨水期Q=122.2 L/s)之后，受水力参数不同步性与统计范围限制，增长速率变缓，直到t=5.42 h(涨水期Q=62.3 L/s)后达到稳定，约为9.2Ld1。冲坑宽度在涨水期t=(1.75～2.17)h呈线性的急速增长，随后呈台阶状缓慢增长，这是由于冲坑的整体发展与变化是由上下游两侧边界共同决定的；到t=3.83 h(落水期Q=181.2 L/s)时，冲刷坑的宽度达到最大值，约为2Ld1，并且在之后的流量过程中不再变化。

3.3.2 波峰起冲条件下的发展规律

图10给出了波峰起冲条件下的冲坑尺度随时间变化。对于冲坑面积随时间变化，冲坑在开始的5 min内高速发展，其面积在t=1.5 h(落水期Q=77.4 L/s)前呈先增长后稳定再增长的变化趋势；随着上游来流量的减小，冲坑面积逐渐不再变化，直到t=4.75 h(涨水期Q=75.0 L/s)，冲坑面积随流量的增大又呈线性快速增长趋势。

图10 波峰起冲条件下的冲坑尺度随时间变化Fig.10 Scale variation of scour pit with time underthe condition of peak inflow process

对于冲坑长度和宽度随时间变化，在t=(0～4.75)h时，冲坑长度变化与面积变化具有相同的趋势；在t=4.75 h后，冲坑长度随流量的增大而增大，增长速率呈两段式，结合图7(b)可见，这与冲坑边壁坍塌及坝后狭长淤积带有关；当冲刷结束时(t=6 h)，冲坑长度可达11.3Ld1，由于此时流量达到最大，冲刷并未达到稳定，冲刷坑长度有继续增长的趋势。冲刷坑宽度的增长与波谷起冲条件下具有相似性，均为在线性高速增长后呈台阶状缓慢增长，其成因与波谷起冲也基本相同；不同之处在于，当t=0.83 h(落水期Q=136.6 L/s)时，由于上游来流量在一段时间内均较小，冲坑发展极为缓慢，冲坑最大宽度暂时保持稳定；直到t=5.75 h(涨水期Q=175.4 L/s)时，流量的持续增大导致床面受到较高流速水流的持续冲刷，冲坑最大宽度才有所加宽，可达2.1Ld1。

4 结 论

(1)不同流量过程下，坝后主流区和回流区的流速均随上游来流量的变化而变化，波谷起冲时主流区随冲刷历时的增加逐渐分为2个区域，而波峰起冲时主流区在初期便被分为2个区域；波谷起冲时涨水期的回流区尺度较落水期大，而波峰起冲大流量时涨水期的回流区尺度较落水期小。

(2)受主流区变化和冲坑后方淤积区的共同影响，波谷起冲时的冲坑下游边界向下游凸起后回缩，波峰起冲时的冲坑边界向坑内收缩后扩散到下游；6 h冲刷历时中，波谷起冲、波峰起冲时最大冲深分别可达9.75 cm和11.99 cm，较恒定流时增加25.5%～54.3%。

(3)非恒定流条件下的冲坑平面尺度呈台阶式线性增长，若以一级丁坝长度Ld1来表征冲坑尺度，单个冲刷周期中(6 h)，波谷起冲时冲坑长度、宽度最大值分别可达9.2Ld1和2Ld1，波峰起冲时则分别可达11.3Ld1和2.1Ld1。