一类Lorenz型系统中的混沌分析
杨文杰,张 帆,郑前前
(许昌学院 数理学院,河南 许昌 461000)
1963年气象学家Lorenz对气象模型进行数值模拟时发现了一种奇怪的吸引子-Lorenz吸引子[1].它的出现引发了人们对混沌现象的研究并提出了一系列的混沌系统[2].
时滞通常是指系统状态的预期发展不仅取决于现在和将来的时间状态,也关系到过去的时间状态.它影响着人们生活的方方面面,无论是生物体受到外部刺激的反应过程,还是生物医学、航空航天、工程设计、机械制造以及电子通信等领域中的反应过程,物理化学等领域的科学研究和建设过程都不可避免受到时滞的影响[3].而且,不同系统中的时滞对系统的影响不同,这意味着在研究分析和探索这些实际系统时,时滞是一个不可忽视的重要研究对象.譬如,研究发现在一些非线性系统中,时滞可以引起系统的解产生振荡不稳定性[4],说明了时滞可以使得Vander Pol-Duffing Oscillator中产生周期运动等现象[5].而这些现象或运动直接影响着诸如生育节律性、相位反转、径向俘获、相位跳跃和振幅空间中的螺旋模式等.因此,研究时滞对系统的影响具有很好的实用价值.
1 模型
Calderon-Saavedra等人给出了一个新的Lorenz型系统[2],主要研究了该系统中的分岔从超临界转变成亚临界的条件,最后证明了受干扰系统经受亚临界Hopf分岔的控制律.然而,该系统在时滞影响下的现象值得研究,为此,考虑在该系统中加入时滞变量τ构成新的Lorenz型系统,具体形式为
(1)
其中x,y,z为状态变量,a,d,b,f,g为系统参数,τ(>0)为时滞量,a>0,f≥0,g≥0,且f+g>0,b,d∈R.下面考虑在具有时滞的情况下,该系统Hopf分支产生的条件、方向以及周期解的稳定性,这些结果在物理、化学或生物系统中有着很广泛的应用.
2 系统平衡点的稳定性分析
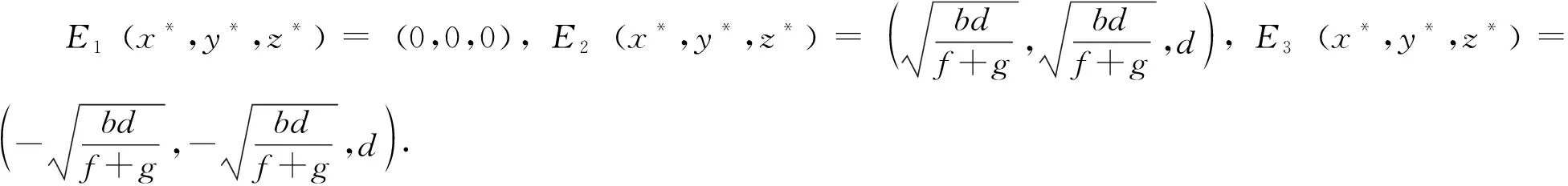
令u1(t)=x(t)-x*,u2(t)=y(t)-y*,u3(t)=z(t)-z*,从而可将平衡点平移到原点处,并得到其在原点处的线性化系统为
(2)
且可得系统(2)的特征方程为
-λ3+q1λ2+q2e-λτλ2+q3λ+q4e-λτλ+q5e-λτ=0,
(3)
其中q1=d-b,q2=-a,q3=bd-gx*2,q4=ad-ab-az*,q5=abd-2afx*2-agx*y*-agx*2-abz*.
当τ=0时,由Routh-Hurwitz判据可知,若q5<0,q1+q2<0,(q1+q2)(q3+q4)>-q5则有
①当E=E1时,系统的平衡点是渐进稳定的;
②当E=E2或E=E3时,方程(3)至少有一个正实根,因此E2和E3均是不稳定平衡点.
因而,下面只讨论平衡点E=E1的情况.
令iω(ω>0)是方程(3)的特征根,代入(3)得
-(iω)3+a1(iω)2+a3(iω)2e-iωτ+a3(iω)+a4(iω)e-iωτ+a5e-iωτ=0,
令v=ω2,可得
G(v)=v3+e1v2+e2v+e3,
(4)
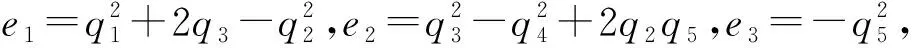
G′(v)=3v2+2e1v+e2.
从而,得到如下的结论.
引理1 对于方程(4),有
①若e3<0,则(4)至少有一个正根;
②若e3≥0,则(4)至少有一个正根当且仅当z*>0,使得G′(v*)=0且G(z*)≥0.
若系统(1)的系数均给定,运用MATLAB软件,可以很容易算出(4)的所有根.
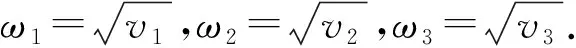
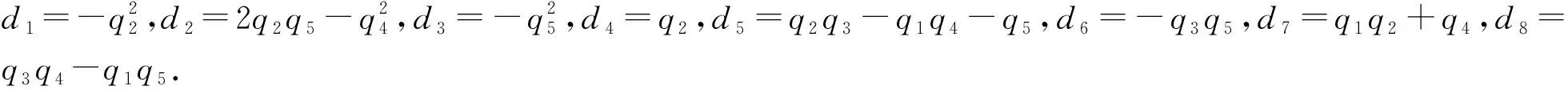
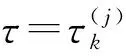
由以上的结论与假设,结合Ruan与Wei在文[6]中的结论可以得到.
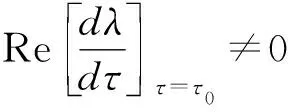
①当τ∈[0,τ0)时,系统(1)的平衡点是渐近稳定的,
②当τ>τ0时,系统(1)的平衡点是不稳定的,
③当τ=τ0时,系统(1)出现Hopf分支.
证明对于特征方程(3),当τ=0时,若q5<0,q1+q2<0,(q1+q2)(q3+q4)>-q5,则当E=E1时,系统的平衡点是渐进稳定的.
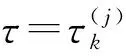
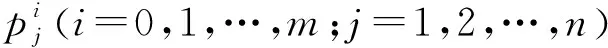
3 分支周期解的稳定性和分支方向
为进一步计算并讨论Hopf分支的方向和分支周期解的稳定性.设t=τt,且μ=τ-τk,则μ=0为系统(1)的Hopf分支值.考虑其等价系统
其中x=(u1,u2,u3)T∈R3,L(μ)是C([-1,0],R3)到R3上的连续映射.由Riesz表示定理及Hassard方法[7],可得
它们决定着中心流形上分支周期解在临界值τk处的性质.即μk确定分支周期解的方向,若μ2>0(<0),则Hopf分支为上临界(下临界)分支且分支周期解出现在τ>τ0(<τ0);β2确定分支周期解的稳定性,若β2<0(>0),则分支周期解是稳定的(不稳定的);T2确定分支周期解的周期,若T2>0(<0),则其分支周期解的周期是增加的(减少的).
4 数值模型分析及结论
为了验证前面的理论结果,考虑如下的时滞系统
(5)
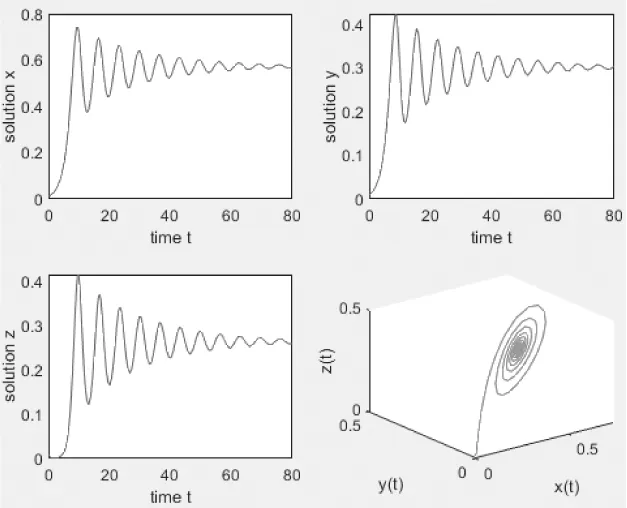
图1 系统(5)在τ=0.158 5时的轨迹及相图
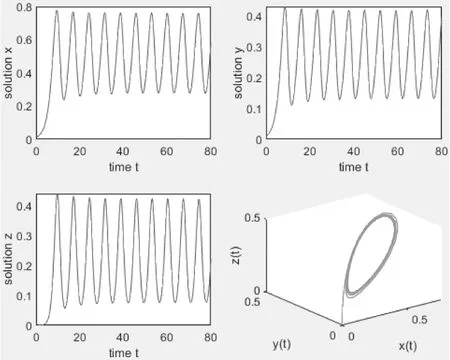
图2 系统(5)在τ=0.337 4时的轨迹及相图
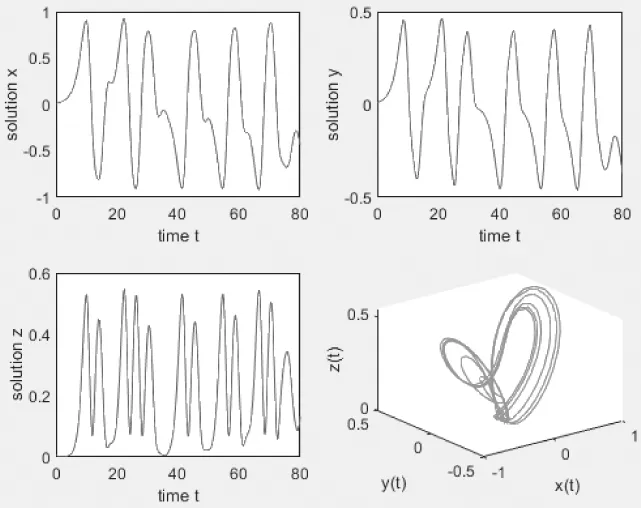
图3 系统(5)在τ=0.737 4时的轨迹与相图
通过研究一类具有时滞的Lorenz型系统.首先,分析了系统平衡点的局部稳定性和Hopf分支的存在性,得到了当以τ为分支参数时系统的局部渐近稳定、不稳定、Hopf分支发生的条件.进一步得到了关于Hopf分岔的一些显式公式.其次,发现了μ2决定Hopf分支的方向,β2决定分支周期解的稳定性,T2确定分支周期解的周期.最后,通过数值模拟验证了理论分析的正确性.

