A Kind of Integral Representation on Complex Manifold

Teqing Chenand Zhiwei Li

1School of Information Management,Minnan University of Science and Technology,Shishi 362700,China;

2School of Mathematics and Computer Science, Quanzhou Normal University,Quanzhou 362000,China.

Abstract.In this paper,by using the Hermitian metric and Chern connection,we study the case of a strictly pseudoconvex domain G with non-smooth boundaries in a complex manifold.By constructing a new integral kernel,we obtain a new Koppelman–Leray–Norguet formula of type(p,q)on G,and get the continuous solutions of¯∂–equations on G under a suitable condition.The new formula doesn’t involve integrals on the boundary,thus one can avoid complex estimations of the boundary integrals,and the density of integral may be not defined on the boundary but only in the domain.As some applications,we discuss the Koppelman–Leray–Norguet formula of type(p,q)for general strictly pseudoconvex polyhedrons(unnecessarily non-degenerate)on Stein manifolds,also get the continuous solutions of¯∂–equations under a suitable condition.

Keywords:Complex manifold, strictly pseudoconvex domain,non-smooth boundary,Koppelman–Leray–Norguet formula,¯∂–equation

1 Introduction

As early as 1831,Cauchy found the famous Cauchy integral formula,which named by his name.Many mathematicians were aware of the importance of integral representation in complex analysis.Later,the integral representation method gradually became one of the main methods of complex analysis in several variables,because one of its main virtues is that it is easy to estimate like the Cauchy integral formula in one complex variable.It is well known that the integral representations and their applications for(0,q)differential form in Cnhave been deeply studied(see,for instance[1–10]).But the research for integral representations on complex manifolds began in 1980s.Most of the results,so far,have been concerned with Stein manifolds(see,for instance[4,5,11-13]).In the early 1990s,Berndtsson B[14]studied the theory of integral representations on general complex manifolds and gained in a quite general integral kernel under a suitable condition.Using this kernel,the Koppelman formula on complex manifolds was obtained.Based on it,Zhong T[15]got the Koppelman–Leray–Norguet formula of type(p,q)on a bounded domainGwith piecewiseC1smooth boundaries in a complex manifold,and gave the continuous solutions of¯∂–equations onGunder a suitable condition.

In this paper,by using the Hermitian metric and Chern connection,the case of a strictly pseudoconvex domainGwith non-smooth boundaries in a complex manifold is studied.By constructing a new integral kernel,a new Koppelman–Leray–Norguet formula of type(p,q)onGis obtained,and the continuous solution of¯∂–equations onGunder a suitable condition is given.The new formula doesn’t involve integrals on the boundary,thus complex estimations of the boundary integrals can be avoided,and the density of integral may be not defined on the boundary but only in the domain.As an application,Cnand Stein manifold are taken as examples to discuss the relationship between the conclusion of this paper and the corresponding conclusion in[4].The Koppelman–Leray–Norguet formula of type(p,q)for general strictly pseudoconvex polyhedrons with unnecessarily non-degenerate on Stein manifolds is also discussed,and the continuous solution of¯∂–equations under a suitable condition is given,it implies the corresponding result in paper[13].

2 Basic knowledge and lemma

3 New Koppelm an–Leray-Norguet formula

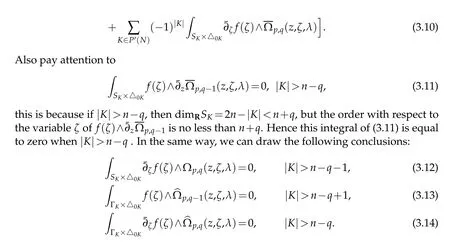
If Θe=D2e=0,then we haveQp,q(z,ζ,λ)=0,Cn[Θ]p,q(z,ζ)=0.From Lemma 3.2,Lemma 3.3,formula(3.10)to(3.14)and Koppelman–Leray–Norguet formula(Lemma 2.1),the formula(3.6)holds whenζ∈∂Gand dρk(ζ)0.

Second,we consider the general case that we do not have to assume dρk(ζ)0,(k=1,···,N),whenζ∈∂G.In this case,we prove the theorem by considering a sequence of strictly pseudoconvex domainsGmwhich are in finitely close toG.And all constructions in this section are uniform convergence with respect tom.From this we complete the proof of the Theorem 3.1.

Example 3.1.IfM=Cn,then the vector bundleEis chosen as an trivial bundle of ordern,the sectionηis usually chosen asη=ζ−z,andξkis chosen as the section of the Cauchy–Leray vector bundle.It is clear that the corresponding results for strictly pseudoconvex domains with non-smooth boundaries in Cncan be obtained from Theorem 3.1,it contains the Theorem 3.1.3 in paper[4].

Example 3.2.IfMis a Stein manifold of complex dimensionn,Gis a strictly pseudoconvex domain with non-smooth boundary inM,s(z,ζ),ϕ(z,ζ),κis the same as Lemma 4.2.4 in paper[4],T(M)andT∗(M)are the complex tangent bundle and the complex cotangent bundle ofM,respectively,(M)and∗(M)are pullback maps ofT(M)andT∗(M)with respect to projectionM×M→M,(z,ζ)z.EandE∗are chosen as(M)and∗(M),respectively.The sectionsξ1, ···,ξNofE∗,which are taken asrespectively.We choose holomorphic cross sectionη=s(z,ζ)such that{η=0}=Y∪P,wherePis a closed set disconnected toY,the exceptional zero point ofηleads to new difficulty.To overcome this difficulty,we introduce a holomorphic functionϕ,which has the propertyϕ(z,z)=1.From Theorem 3.1,we obtain Koppelman–leray–norguet formula with weight factorϕν(z,ζ)(ν≥max{nκ∗,nκ}).This is the corresponding result of strictly pseudoconvex domain with non-smooth boundary in Stein manifolds.It contains Theorem 4.10.4 in paper[4].

4 New formula for general strictly pseudoconvex polyhedron on Stein manifold

Acknowledgments

This work was supported by Educational and Scientific Research Funding Program for young and middle-aged teachers in Fujian Province,China(Grant No.JT180700).