Gradient Bounds for Almost Complex Special Lagrangian Equation with Supercritical Phase

Jiaogen Zhang

School of Mathematical Sciences,University of Science and Technology of China,Hefei 230026,China.

Abstract.In this article,we will consider the Dirichlet problem for special Lagrangian equation on Ω⊂M,where(M,J)is a compact almost complex manifold.Under the existence of C2-smooth strictly J–plurisubharmonic subsolution u,in the supercritical phase case,we obtain a uniform global gradient estimate.

Key words:Special Lagrangian equation,almost complex manifold,gradient estimates,maximum principle.

1 Introduction

In this paper,we consider the Dirichlet problem for the special Lagrangian operator,in the real setting which can be written as the the form

Here Θ is a topological constant called the phase angle,D2uis the real Hessian ofu.Under the coordinate system{x1,···,xn},D2ucan be regarded as the matrixAfter an elementary orthogonal transformation,

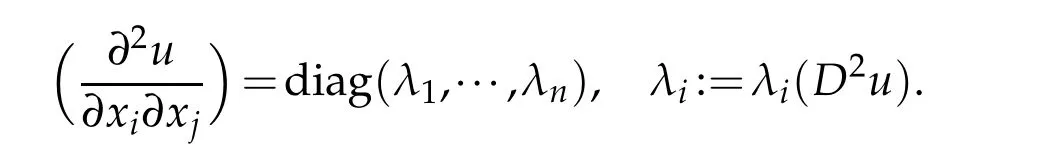
Eq.(1.1)was introduced by Harvey–Lawson[10]when they studied the Calibrated geometry.In this case,the gradient graphx(x,Du(x))defines a calibration and also determines a Lagrangian graph,which is a minimal submanifold of Rn×Rn.In fact,anyC2Lagrangian submanifoldM2nis locally represented by a gradient graph(x,Du(x))over its tangent plane.The interested reader can also refer to the Warren’s PhD thesis[25]for more details of this topic.The investigation of Lagrangian manifolds also has many important applications in both geometry and physics,especially the works done by Stromingeret al.[24]about mirror symmetry,which gave a very geometric picture of how mirror manifolds are connected.

In the real setting,the Dirichlet problem for Eq.(1.1)on smooth domain with strictly pseudoconvex boundary was also considered by Cafferalli–Nirenberg–Spruck[1]whenMoreover,they also showed that the special Lagrangian operator is concave in this setting.After that,the special Lagrangian equation with supercritical phase has also been studied extensively in the past few years.For instance,Warren-Yuan[26]considered the interior gradient estimates,and the interior second order estimates were obtained by Wang–Yuan[27].For special Lagrangian equations with more general phases,one can refer a serious works of Harvey-Lawson[11,12,14]et al.and references therein.

At the same time,in the complex setting,there were also many excellent works.For instance,Collins–Picard–Wu[4]obtained the existence and regularity theorems under the existence of subsolution for the Dirichlet problem,in both of real and complex cases.Dinew–Do–Tˆo[8]also obtained a continuous viscosity solution by using the classical Perron’s envelope method.The complex special Lagrangian equation has an intimate connection with the deformed Hermitian-Yang-Mills equation.The interested reader can refer to[17–19]et al.for more profound understanding.

It is remarkable that the almost complex manifold has been studied extensively during past few years,which is motivated by differential geometry and mathematical physics([6,13]and references therein).In the current note,we wish to investigate the Dirichlet problem for special Lagrangian equation on the almost complex manifold.

Let(M,J)be a compact almost complex manifold of real dimension 2n,and Ω⊂Mbe a smooth domain with smooth boundary∂Ω.Fix a Hermitian metricωonM.We wish to consider the Dirichlet problem for the almost complex special Lagrangian operator which can be written in the following form

Hereϕ,hare given functions onλ1,···,λnare the eigenvalues ofwith respect toω.

We now state our main result.Assumei.e.,thesupercriticalphase case,we have the following global gradient estimates,under the existence ofC2subsolution.

2 Preliminaries

2.1 Basic technique

2.2 Comparison principle

2.3 Existence of subsolution

3 C0and C1estimates

3.1 Uniform estimates

3.2 Boundary gradient estimates

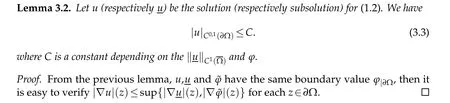
3.3 Interior gradient estimates

Acknowledgments

The author would like to thank his advisor professor Xi Zhang for his constant encouragements.He would also like to thank the referees for many useful suggestions and comments.The author was partially supported by National Natural Science Foundation of China(Grants Nos.11625106,11571332 and 11721101).The research was partially supported by the project“Analysis and Geometry on Bundle” of Ministry of Science and Technology of the People’s Republic of China.