Density Functional Theory for Electrocatalysis

Xiaobin Liao,Ruihu Lu,Lixue Xia,Qian Liu,Huan Wang,Kristin Zhao,Zhaoyang Wang*,and Yan Zhao*

It is a considerably promising strategy to produce fuels and high-value chemicals through an electrochemical conversion process in the green and sustainable energy systems.Catalysts for electrocatalytic reactions,including hydrogen evolution reaction(HER),oxygen evolution reaction(OER),oxygen reduction reaction(ORR),nitrogen reduction reaction(NRR),carbon dioxide reduction reaction(CO2RR),play a significant role in the advanced energy conversion technologies,such as water splitting devices,fuel cells,and rechargeable metal-air batteries.Developing low-cost and highly efficient electrocatalysts is closely related to establishing the composition-structureactivity relationships and fundamental understanding of catalytic mechanisms.Density functional theory(DFT)is emerging as an important computational tool that can provide insights into the relationship between the electrochemical performances and physical/chemical properties of catalysts.This article presents a review on the progress of the DFT,and the computational simulations,within the framework of DFT,for the electrocatalytic processes,as well as the computational designs and virtual screenings of new electrocatalysts.Some useful descriptors and analysis tools for evaluating the electrocatalytic performances are highlighted,including formation energies,d-band model,scaling relation,egorbital occupation,and free energies of adsorption.Furthermore,the remaining questions and perspectives for the development of DFT for electrocatalysis are also proposed.

Keywords

analysis tools,density functional theory,descriptors,electrocatalysis

1.Introduction

With the increase in energy demand and worldwide natural environment crises,it is imperative to develop green and sustainable energy systems to produce clean fuels and chemicals,which can replace fossil fuels and reduce carbon dioxide emissions.[1-3]A promising strategy is to develop advanced electrochemical technologies that can convert some common molecules(e.g.,water,carbon dioxide,and nitrogen)into high-value chemical products(e.g.,hydrogen,hydrocarbons,oxygenates,ammonia,and carbonates).[4-7]The important energy-related electrocatalytic reactions,including hydrogen evolution reaction(HER),oxygen evolution reaction (OER),oxygen reduction reaction(ORR),nitrogen reduction reaction(NRR),carbon dioxide reduction reaction(CO2RR),are the key conversion routes.In the complex processes for the electrocatalytic reactions,an efficient,highly selective,and stable electrocatalyst plays a pivotal role in speeding up the reaction kinetics and decreasing the overpotential,[5,8,9]which can enhance the sustainable energy conversion efficiency.Over the past few decades,tremendous progresses have been made in the establishment of electrocatalysts preparation and fundamental catalytic mechanisms.[6,7,9-18]Nevertheless,those breakthroughs still stay at the stage of experimental synthesis and lack of indepth understanding of fundamental principles of the active site on the catalyst surface and catalytic reactions mechanisms,which seriously limits the development of efficient catalysts.Researchers are full of enthusiasm about preparation of advanced catalysts with ideal properties,expecting to establish the composition-structure-function relationships.Density functional theory(DFT)calculations are based on quantum mechanics,which can calculate the electronic structure of the whole catalytic system.It is probably the most powerful computational approach to investigate the structure-activity relationships of electrocatalysts at atomic level.With the rapid advances of computer technology,DFT calculations have created tremendous opportunities in shedding light on the electrocatalytic mechanisms and predicting promising catalysts.[19,20]

Identification of the active sites and understanding of the reaction mechanisms are the two key aspects for the study of electrocatalytic reactions.[21]For the former,the experimental approach for identifying active sites is indirect by prepared specified catalysts and establishing definite correlations between catalytic performances and controllable factors.[22,23]Actually,many intermediate states of electrocatalytic reactions and electron transfer processes are extremely difficult to probe due to their ultrashort lifetimes and complex reaction conditions.That always makes the active sites indefinite and the corresponding catalytic mechanisms ambiguous.Thus,it is a relatively direct strategy by combining experimental characterizations and DFT calculations to identify the active sites involved in various electrocatalytic reactions.Meanwhile,deeply comprehending the catalytic mechanisms of electrocatalytic reactions can accelerate the screening of potential catalysts.Considerable studies have demonstrated the useful applications of DFT for advanced catalysts predictions and discoveries.We strongly believe that the interplay of theoretical calculations and experimental investigations will effectively change the traditional trial-and-error approach of catalysts design,paving the way for rational designing new advanced electrocatalysts.

In this review,we are introducing the impressive progress of DFT,and the application of DFT in electrocatalysis,which can build a fundamental bridge between structures and activities.The review is organized as follows.The history and development of DFT methods are thoroughly summarized in Section 2.Section 3 provides several representative descriptors developed by DFT calculations,including the binding energy,formation energy,[24-26]d-band center,[27-29]scaling relations,[30-33]egorbital occupation,[34-36]and free energy of adsorption.[37-39]Meanwhile,at Section 4,we will describe the practical tools derived from DFT calculations,which are useful for further investigation of the electrocatalytic activity.Section 5 gives a brief introduction of the catalytic mechanisms of specific electrocatalytic reactions,including HER,ORR,CO2RR,and NRR.At the end,we conclude the review with perspectives for the application of DFT in the research of advanced electrocatalysis.

2.Development and Assessments of Density Functionals

Density functional theory is,in principle,exact theory for the solution of the many-electron Schrödinger equation,but the underlying exchange-correlation functional needs to be approximated.Developing new density functional is an ongoing hot research area because there are still many challenges for the approximated density functionals.Throughout this section,we review the developments and applications of density functionals in electrocatalysis.

2.1.Background of Density Functional Theory

Density functional theory has been considered as the most common approach for the many-electron systems,such as complex organic systems and solids in the form of the electronic density for the threedimensional system.[40]Most of the modern DFT calculations are based on the Kohn-Sham scheme,which involves filling electrons in the N fictitious single-particle spin-orbitals of the non-interacting electrons.By contrast,the wave function theory(WFT)describes the N electrons in the system by a 3N-dimensional antisymmetric wave function.[41]WFT methods are systematically improvable and can give excellent accuracy for small molecules,and sometimes even rival the experiments.However,the computational cost of the correlated WFT methods is prohibitively too high to be applied to the periodic systems with hundreds of atoms,and DFT competes well with WFT in terms of costperformance ratio.

Using “reductio ad absurdum,”Hohenberg and Kohn proved that the ground-state total energy E is a functional of the electron density ρ=ρ↑+ρ↓for the N-interacting-electron system formed by a collection of atoms,where ρ↑and ρ↓are the up-and down-spin electron densities,respectively.Using atomic units(¯h=m=e2=1),the oneelectron Kohn-Sham equation for a system can be written as:

2.2.Density Functionals

Over two hundred approximate functionals have been developed.They can be grouped into five classes:1)local functionals;2)functionals with nonlocal exchange;3)functionals with nonlocal van der Waals correlation;4)doubly hybrid functionals;and 5)functionals with molecular mechanics dispersion.

2.2.1.Local Functionals

The popular representations of the UEG ec（rs,ζ）,for example,VWN80,[53]PZ81,[56]and PW92,[51]have been developed by fitting to the Quantum Monte Carlo(QMC)data of Ceperley and Alder,[57]but they do not recover the low-density limit expansion(Eq.15).Recently,our group have developed an nonempirical analytical representation of the W20(stands for Wuhan 2020)UEG ec（rs,ζ）by using an interpolation ansatz without any fitting parameters.The elegant W20 ansatz is employed to interpolate the high-and low-density limits(Eqs.13 and 15).The comparative assessments against the QMC data of Spink et al.[58]have shown that W20 performs better than VWN80,PZ81,and PW92 for the low-density regions.

As the LSDA assumes that the density is the same everywhere as in UEG,it performs considerably well in the solid system,giving reasonably accurate lattice constants,but fails to describe the chemistry involving atoms and molecules.[59,60]The errors originate from the underestimation of the exchange energy and overestimation of the correlation energy in LSDA.[61]The next step of taking the inhomogeneity into consideration is to add the gradients of the spin densities∇ρ↑and∇ρ↓to the functional form.Surprisingly,the second-order gradient expansion approximation(GEA)gives worse performance than LSDA.Langreth and Perdew[62]explained that the GEA for correlation energy is failed by using a wave-vector analysis.In order to overcome the problems in GEA,the generalized gradient approximations(GGAs)[63-66]have been proposed and are widely used in quantum chemistry.One of the early popular GGAs in organometallics is BP86,where B denotes Becke’s 1988 exchange GGA functional(usually abbreviated as B88 or B),[64]and P86 is Perdew’s 1986 GGA correlation functional.[63]Some popular GGAs are the Lee-Yang-Parr(LYP)functional[65]and the PBE functional of Perdew,Burke,and Ernzerhof.[66]Although having the same ingredients as GGAs,the non-separable gradient approximations(NGAs)[67]employ a more general functional form than GGAs,and the UEG terms and the density gradients enhancement factors are not separated in NGAs.N12[67]and GAM[68]are the representative NGAs.The more complex local density functionals are the meta-GGAs,which depends on the orbitals in the form of the spin kinetic energy densities(τ↑and τ↓)and/or the Laplacian of the density.Some popular meta-GGAs include the Becke95 correlation functional,[69]TPSS,[70]SCAN,[71]M06-L functional of Zhao and Truhlar,[72]MN15-L,[73]HLE17,[74]and revM06-L.[75]

2.2.2.Functionals with Nonlocal Exchange

The main challenge for conventional local functionals is the selfinteraction error(SIE).[56,76]One way to alleviate this problem is to combine a fraction of Hartree-Fock exchange(nonlocal exchange)with pure DFT functionals.The functionals with nonlocal exchange include global hybrid GGAs,screened-hybrid GGAs,screened-hybrid NGAs,global hybrid meta-GGAs,and global hybrid meta-NGAs.[77,78]In these functionals,a percentage X of local exchange is replaced by HF exchange,where X is a global constant,and the general formula can be written as:

2.2.3.Functionals with Nonlocal van der Waals Correlation

2.2.4.Doubly hybrid functionals

The combination of WFT and DFT(also denoted as doubly hybrid functionals)is an effective way to achieve better accuracy with less computational cost.[110]The “doubly hybrid”is first coined in the MC3-type functionals of Zhao and Truhlar,[111]where the MC3 is the abbreviation of “multi-coefficient three-parameter.”In the MC3-type doubly hybrid functionals,a fraction of second-order Møller--Plesset(MP2)correlation energy based on the HF orbitals with a small basis set is mixed with a hybrid DFT energy with a large basis set,and this combination significantly reduces the computational cost.

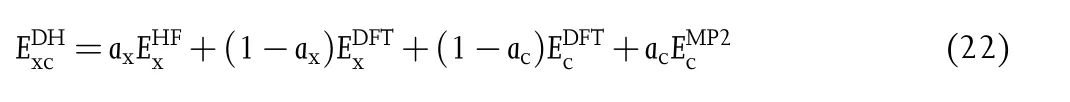
In the Grimme’s double-hybrid density functionals(DHDFs),[112-114]the Kohn-Sham orbitals are employed for computing the MP2 correlation energy,where axand acare two empirical parameters,and they are optimized against the G2 set of experimental heat of formation in the first DHDF,B2-PLYP.[113]Later,Grimme’s group developed the MPW2-PLYP-D,[115]PWPB95-D,[116]and PTPSS-D[116]DHDFs.Martin’s group have developed a large number of DHDFs,and they are reviewed in a recent paper.[117]Zhang et al.have employed the B3LYP orbitals for the MP2 correlation energy calculation in their XYG3 and XYG3-OS DHDFs.[118]Mardirossian and Head-Gordon have combinatorically optimized the ωB97M(2)DHDF,[119]which employs the range-separated DFT orbitals for the MP2 correlation energy.Some DHDFs have been developed without empirical fitting parameters,for example,PBE0-DH(2011)[120]and PBEQIDH(2014),[121]and they are reviewed in a recent paper of PBE0-QIDH.[122]

2.2.5.Functionals with Molecular Mechanics Dispersion

There are some other DFT-D methods which have been developed to calculate the C6coefficients for each atom pair in a molecule.The Tkatchenko-Scheffler(TS)method[125-127]employed the atomic volumes,and Sato et al.[128,129]developed a method to calculate the C6coefficients based on the local response approximation of Dobson and Dinte.[130]Becke and Johnson[131,132]have developed the exchangehole dipole moment(XDM)method for computing the systemdependent C6coefficients.

The widely used DFT-D methods include PBE-D3,B3LYP-D3,ωB97X-D(range-separated GGA+MM),[133]APF-D(global hybrid GGA+MM),[134]PW6B95-D3(global hybrid meta-GGA+MM).[87]Some DHDFs have been developed with molecular mechanics dispersion,for example,DSD-PBEP86,[135]mPW2-PLYP-D,[115,123]and B2-PLYP-D3.[116]

Perdew proposed a “Jacob’s ladder” for density functional approximations,[136,137]which is a ladder from the Earth(Hartree world)to Heaven(chemical accuracy)(Figure 1).All the density functionals can be ordered by the “Jacob’s ladder” according to the complexity of the exchange-correlation functionals.The first rung of the ladder is completed by the LSDA which only depends on spin densities.GGAs and NGAs complete the second rung,in which the local spin density gradients are added into their constructions.The meta-GGAs are on the third rung,and spin kinetic energy densities and/or the Laplacians of densities are added to the constructions.[138]The fourth rung is more complex and completed by the hybrid density functionals,which contains a fraction of HF exchange.Doubly hybrid functionals complete the fifth rung,which employs the virtual orbitals for the exchange-correlation energy calculations(e.g.,MP2 correlation energy).

Figure 1.Jacob’s ladder of density functional approximations.

2.2.6.Software

A variety of quantum chemical software packages have been developed to predict the properties of various compounds and reactions.Most of the popular DFT computer programs are summarized in Table 1.Among them,the Gaussian program based on the Gaussian basis set is the most widely used package for the chemistry community,and the Vienna Ab initio Simulation Package(VASP)is the most popular package for physics and materials science.Furthermore,The DMol3 code developed from a numerical basis can be used for calculations of isolated molecules and for solid and surface with low computational cost.In order to reduce the computational cost,the relative inert core electrons are usually treated with the effective core potential(ECP),[139]pseudopotentials,[140]and projector-augmented wave potentials(PAW)methods.[141]

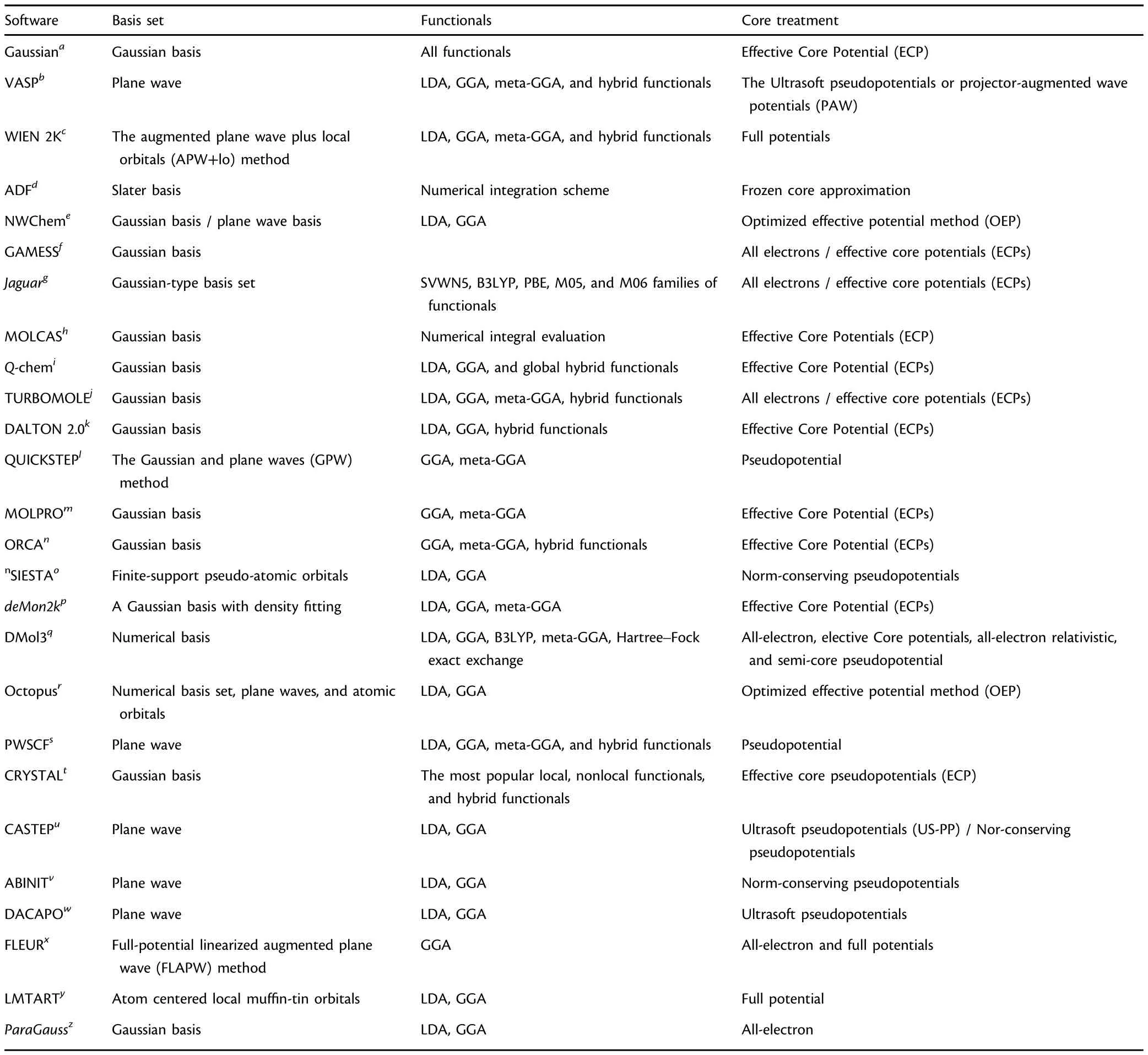
Table 1.Software and the related basis set,functionals,and core potential.

2.3.General performances of density functionals for catalysis

A major difficulty in choosing density functionals for applications in electrocatalysis is that density functionals are not systematically improvable.This section is focused on the assessment of different functionals,including atomic and molecular systems,transition metal systems(pure metal and compounds),and absorptions.

2.3.1.Databases

In the past decades,many databases for different properties have been developed and collected for the developments and assessments of density functionals,including atomization energies,reaction barriers,lattice constants,and band gap.Common Database 2.0 of the Truhlar group[142]consists of CE345(chemistry energetic database with 345 data),PE39(physics energetic database with 39 data),CS20(chemistry structural database with 20 data),and PS47(physics structural database with 47 data).It evolves into Minnesota Database 2019,[143]which comprises of a diverse set of chemical data,and is divided into a primary collection of 31 subdatabases and an auxiliary collection of 25 subdatabases.The GMTKN55(GeneralMain-groupThermochemistry,Kinetics,andNon-covalent interactions database,55subsets) database[144]is collected by the Grimme group,which consists of 1505 diverse relative energies.Head-Gordon’s group collected MGCDB84(Main-Group Chemistry Database),which comprises of 84 diverse datasets of 4986 relative energies.[145]It is worth noting that the three databases(Minnesota 2019,GMTKN55,and MGCD84)have considerable overlaps.

2.3.2.Atomic Energies and Main-Group Chemistry

The performance of the density functionals for atomic energies is highly relative to electrocatalysis,for example,HER,ORR.In Minnesota Database 2019,there is the AE17 set of 17 atomic energies.The performances for the AE17 databases summarized in Table 2,in which the functionals with MUEs(mean unsigned errors)below 5.2 kcal mol-1are listed,including the PW91 GGA,the B3PW91,B98,MPW3LYP,and SOGGA11-X global hybrid GGAs,the MPWKCIS1K,M06-2X,M08-HX,and M08-SO global hybrid meta-GGAs,and the MN12-SX range-separated hybrid meta-GGA.These are the best functionals for atomic energies calculations.

Table 2.The best functionals for the AE17(atomic energies)databases.The data are extracted from Ref.[142].

For molecular systems,Peverati and Truhlar[142]have summarized the performances of density functionals for the MGAE109/11 subset of main-group atomization energies.The best functionals for the MGAE109/11 database are M06-2X,PW6B95,ωB97X,MN12-SX,ωB97X-D,M11,and BMK,with MUEs in the range of 0.50±0.03 kcal mol-1per bond.For the NCCE31/05 subset of noncovalent interactions,M11,PWB6K,M05-2X,M06-2X,and MN12-SX all show remarkable MUEs of 0.30 kcal mol-1or less.Grimme and coworkers assessed 84 functionals with and without dispersioncorrelation for the GMTKN55 databases.[144]If we use the WTMAD-1(weighted total mean absolute deviations 1)value as the metric for performance,the best performing functionals without molecular mechanics dispersion correction for the GMTKN55 databases are M05-2X,M06,M06-2X,M08-HX,M11,MN15,B2GPPLYP,[151]PWPB95,[116]DSD-BLYP,[152]DSD-PBEP86,[135]and DSD-PBEP95,[153]with the WTMAD-1 average errors below 4 kcal mol-1.The performances are remarkably improved by adding the molecular mechanics dispersion energies to the DFT energies.The best performing dispersion-corrected density functionals are PW6B95-D3(BJ),M052X-D3(0),M062X-D3(0),M08HX-D3(0), ωB97X-D3(0)and ωB97X-V,B2PLYP-D3(BJ),B2GPPLYP-D3(BJ),MPW2PLYP-D3(BJ),PWPB95-D3(BJ),DSD-BLYPD3(BJ),DSD-PBEP86-D3(BJ),and DSD-PBEB95-D3(BJ),with the WTMAD-1 values below 3 kcal/mol.The D3 tail with(0)and(BJ)denoted that the dispersion-correlation is used either with the original damping function(D3(0)),or the Becke-Johnson(BJ)damping function.[116]Mardirossian and Head-Gordon reported an extensive assessment of 200 density functionals on the first four rungs of Jabcob’s ladder for the MGCDB84 database.[145]The database is divided into eight categories:NCED(non-covalent interactions for dimers),ID(difficult isomerization energies),NCEC(non-covalent interactions for clusters),TCE(thermochemistry energies),NCD(difficult non-covalent dimer interactions),TCD(difficult thermochemistry data),IE(isomerization energies),and BH(barrier heights).As shown in the Figure 2,the GGAs show the large errors and are not recommended for practical applications.The B97M-rV functional in the meta-GGA row shows an acceptable performance,but most of the meta-GGAs functionals perform much worse than the hybrid functionals.

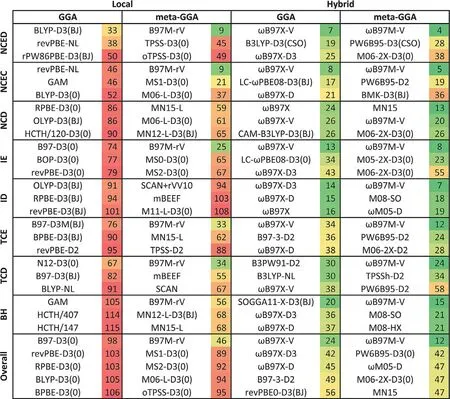
Figure 2.The average RMSDs(Root Mean Square Deviations,in kcal mol-1)of the best functionals for the MGCDB84 databases.The functionals are partitioned by type(local/hybrid and GGA/mGGA)and ranked for each of the datasets that correspond to the eight data types.The overall row is an average over the eight average data type ranks.Reprinted with permission from Ref.[145]Copyright 2017,Taylor and Francis Ltd.

In summary,the assessments of the Truhlar,Grimme,and Head-Gordon groups for relative energies in main-group molecular systems give the performance trends of density functionals consistent with Jacobb’s ladder.Most of the best performing functionals for GMTKN55 and MGCDB84 are DHDFs,belonging to the highest rung of Jacobb’s ladder.

2.3.3.Transition Metal Solid

Transition metals play very important roles in electrocatalysis,and this section is focused on the performances of density functionals for transition metal solids.In 2004,Staroverov et al.have compiled a dataset of lattice constants for 18 solids,including four transition metals,Cu,Rh,Pd,and Ag.This subset has been named as TMLC4(TransitionMetalsLatticeConstants).[154]Figure 3 presents the MUEs of 35 density functionals for TMLC4,which are taken from the review article of Peverati and Truhlar.[142]As shown in Figure 3,the best performing functionals for the TMLC4 databases are MN12-L,revTPSS,[155]PBEsol,[156]N12-SX,SOGGA,TPSS,MN12-SX,N12,and VSXC,[157]with MUEs below 0.04˚A.Similar results are found in the works of Perdew et al.[156]and Csonka et al.[158]Haas et al.[159]compiled a large set of lattice constants for 60 solids,and SOGGA and PBEsol are the two best performing functionals.Paier et al.[160]have shown that PBE0 and HSE03 give better performances for TMLC4 than PBE but B3LYP fails for metals.In 2018,Jana et al.assessed the performances of GGAs(PBE,PBEsol[156])and meta-GGAs(TPSS,modTPSS,[161]oTPSS,[162]revTPSS,regTPSS,[163]M06-L,MS0,MS1,MS2,SCAN,[71]TMTPSS,[164]TM)for predicting the lattice constants,bulk moduli,and cohesive energies of transition metals from 3d to 5d.[165]For the lattice constants,PBE and modTPSS are the best performing functionals for 3d transition metals,whereas revTPSS and regTPSS are the best performing functionals for 4d and 5d transition metals.For the bulk moduli,the PBE and modTPSS are the best performing functionals for 3d transition metals,and TPSS is the best performing functional for 4d transition metals,and PBEsol is the most accurate for 5d transition metals.For cohesive energies,PBE is the best performing functional for 3d and 5d transition metals,and TPSS is the best for 4d transition metals.

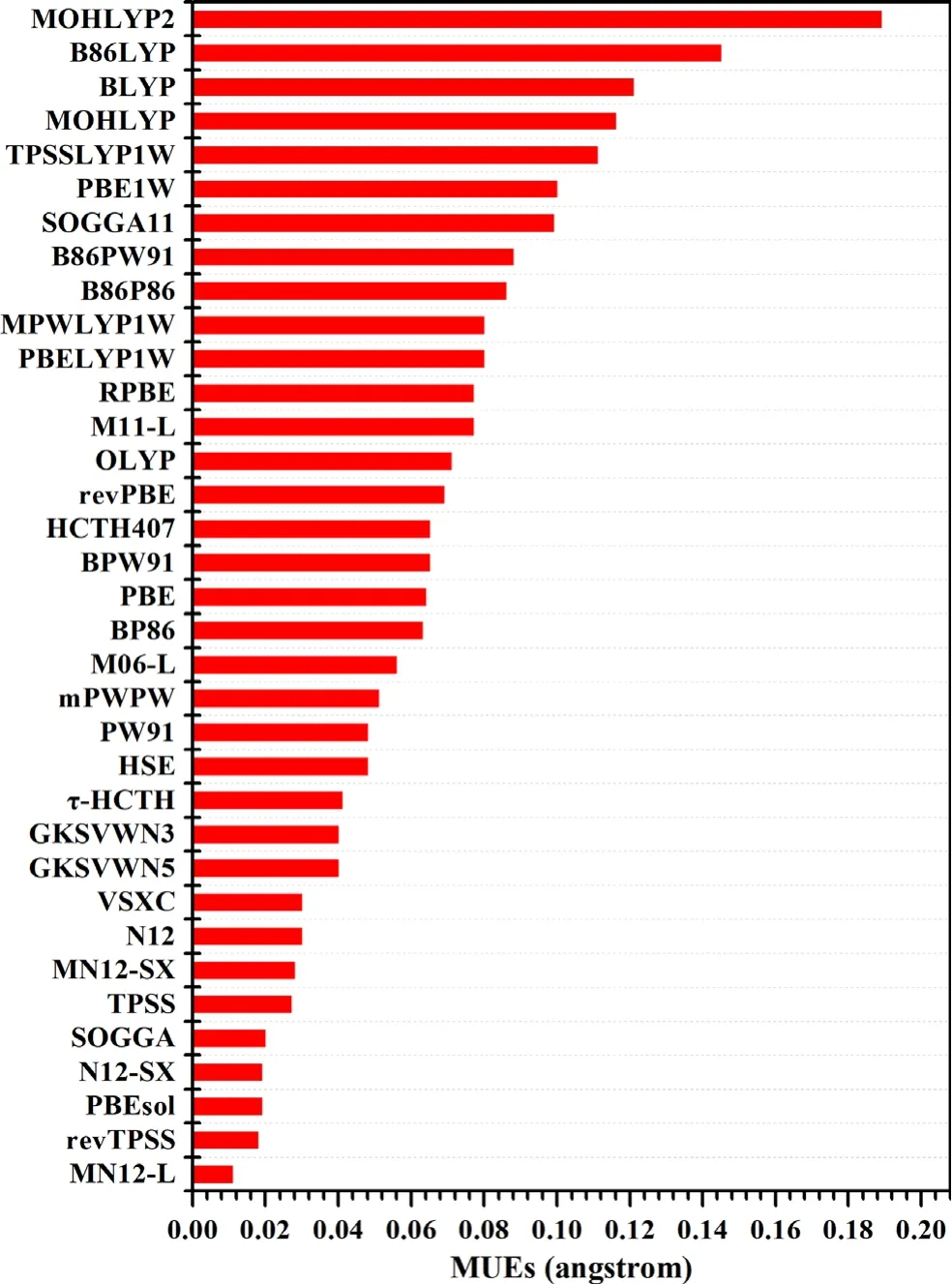
Figure 3.MUEs for the transition metals lattice constants database(TMLC4).(All values in angstrom;functionals are ordered according to MUE for TMLC4.).The value is extracted from Ref.[142]

Other important properties of transition metal solids are the surface energy and work function.Meier de Andrade et al.[166]have reported an assessment of LSDA,GGAs,and vdW-DF for the prediction of surface energy and work function of Ni(111),and they found that the LSDA and vdW-DF-cx[107]are the best performing functionals for the surface energy of Ni(111),whereas the PBEsol-D3,PBE-D3,RPBE-D3 functionals overestimate it,and the PBEsol,PBE,RPBE,optPBE-vdW,revPBE,SCAN,SCAN-rVV10 functionals underestimate it.The vdWDF-cx functional is the best performing functional for the work function of Ni,slightly underestimating it.LSDA overestimates the work function of Ni,and all the other tested functionals underestimate the work function.Similar results can be found in the work of De Waele et al.[167]Vega and Viñes evaluated the accuracy of PBE,PBEsol,VV,and VVsol functionals for predicting properties of 27 transition metal bulks and 81 transition metal surfaces;[168]they found that PBE and VV are the best performing functionals for predicting cohesive energies of transition metal bulks,whereas PBEsol and VVsol are the best performing functionals for calculating surface energies,and PBE and PBEsol are the best performing functionals for predicting work function.

2.3.4.Transition Metal Compounds

Transition metal chemistry is more challenging for density functionals than main-group chemistry,due to the complexity of the neardegeneracy multireference characters in most of transition metals.[142,154,169]Self-interaction error[56,76]is one of the major problems in density functional approximations,causing the failure for describing the strongly correlated systems,for example,the systems with localized electron states(d or f orbitals),such as those in the transition metal oxides(TMOs).[170]It is generally accepted that the strong correlations may be described by adding the system-dependent Hubbard parameters U.[171]The DFT+U method includes empirical correction terms of the Hubbard Hamiltonian for localized orbitals,[170,172,173]

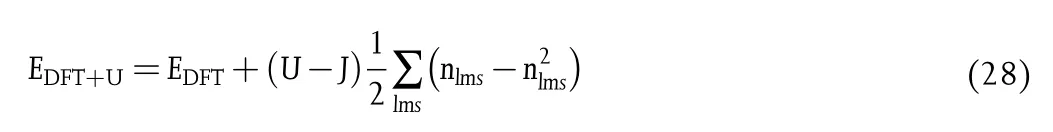
where U is the coulomb potential and J is the exact exchange potential(in principle),and n is the occupation value of an atomic orbital defined by the quantum numbers l,m,and s.In practice,the difference Ueff=U-J is empirically fitted to certain physical properties,such as lattice constants,band gaps,[174]and/or reaction energetics(thermochemistry and kinetics).[175]One must be cautious with the DFT+U approach,and in most instance,it is a trade-off between accurate electronic structure and accurate thermochemistry.Lutfalla et al.[176]have calibrated the PBE+U method for predicting reduction energies for metal oxides of Ti,V,Mo,and Ce.They found that the Ueffparameters optimized against the lattice parameters or band gaps are significantly different from those optimized against the experimental reduction energies,and the use of these Ueffparameters may result in errors in redox energies of over 100 kJ/mol.They also found that,when a transition metal element has more than two oxidation states,the redox energies between different pairs of these states require slightly different Ueffparameters.[176]Getsoian and Bell[177]compared the RPBE+U method to M06-L for predicting the structural and electronic properties of a family of reducible transition metal oxide(RTMO)catalysts:MoO2,MoO3,and Bi2Mo3O12,which are challenging for DFT methods.They found that the performance of M06-L is better than that of RPBE(+U)except that the computational cost of M06-L is moderately higher than RPBE+U by a factor of 4-5 using the VASP software.Significantly,for redox reactions on the surfaces of RTMOs,M06-L exhibits superior performance for predicting reaction barriers and heat of adsorption.The capability of M06-L to capture non-covalent interactions shows potential applications in aqueous electrochemical systems,in which non-covalent interactions play an important role.[177]

Flores et al.[178]studied the crystalline structures and electronic properties of bulk ZnX(X=O,S,Se,Te)by using PBE,PBE+U,and HSE06 functionals.The PBE+U exhibits a relatively larger error in lattice constants than PBE and HSE06,but gives better performance for the prediction of the band gap.Rödl et al.[179]have shown that PBE+U and HSE06 provide accurate results in magnetic properties and band structure of CuO.[179]DFT+U have also been employed in the studies of TiO2,[180]α-MoO3,[181]CeO2,[182]VO2,[183]lanthanum group,[184]and two-dimensional layered disulfide.[185]

In summary,the local and semilocal functionals perform well in the prediction of lattice constants for transition metal systems but usually fail to predict the energy and electronic properties due to selfinteraction errors.GGA+U and hybrid functionals show improved performances for the electronic properties,but the empirical systemdependent Ueffparameters in GGA+U are also property-dependent,meaning different properties require different Ueffparameters.

2.3.5.Absorption properties

In an electrocatalytic reaction,the adsorption properties play a vital role on activity,selectivity,and stability of catalysts.DFT can be employed to calculate adsorption energies of intermediates,active site structures,activation energy barriers,and reaction pathway preferences and mechanisms.However,as pointed out by Schimka et al.,[186]the local and semilocal density functionals tend to underestimate the surface energy and overestimate the chemisorption energies.Optimizing the functionals improves the performance either for the surface energy or the chemisorption energy but worsens the other.A classic example is the “CO puzzle,”which is a longstanding issue in computational surface chemistry.[187,188]In 2001,Feibelman et al.showed that LSDA or GGAs fail to predict the correct adsorption site of CO on Pt(111).[187]Later,Stroppa et al.[189]assessed PBE,BLYP,HSE,and B3LYP for predicting the adsorption of CO on late 4d and 5d transition metals(111)surface(Ru,Rh,Pd,Ag,Os,Ir,and Pt).They found that the PBE-based hybrid functionals predict the correct site order on all the metals except Pt,but significantly overestimate the adsorption energies.The semilocal BLYP and the corresponding hybrid functional B3LYP yield a better prediction of adsorption energies and the correct adsorption site for all surfaces,but both functionals fail to describe the properties of the metals,considerably overestimating lattice constants and underestimating atomization energies.[189]Luo et al.[190]evaluated the performances of six GGAs(PBE,RPBE,PBEsol,SOGGA,SOGGA11,and BLYP)and two meta-GGAs(M06-L and revTPSS[155])for CO adsorption energies and site preferences on five transition metals(Rh,Pt,Cu,Ag,and Pd).[190]As shown in Table 3,M06-L exhibits improved performance for predicting surface formation energies and adsorption energies,and correctly predicts the site adsorption preferences for Rh,Pt,Ag,and Pd.The PBE-type functionals(PBE,RPBE,PBEsol),revTPSS,and SOGGA-type functionals can only correctly predict the site adsorption preference for one or two of five metals.BLYP gives the correct prediction of adsorption sites for on Rh,Pt,Ag,and Pd,but fails to give accurate adsorption energies.

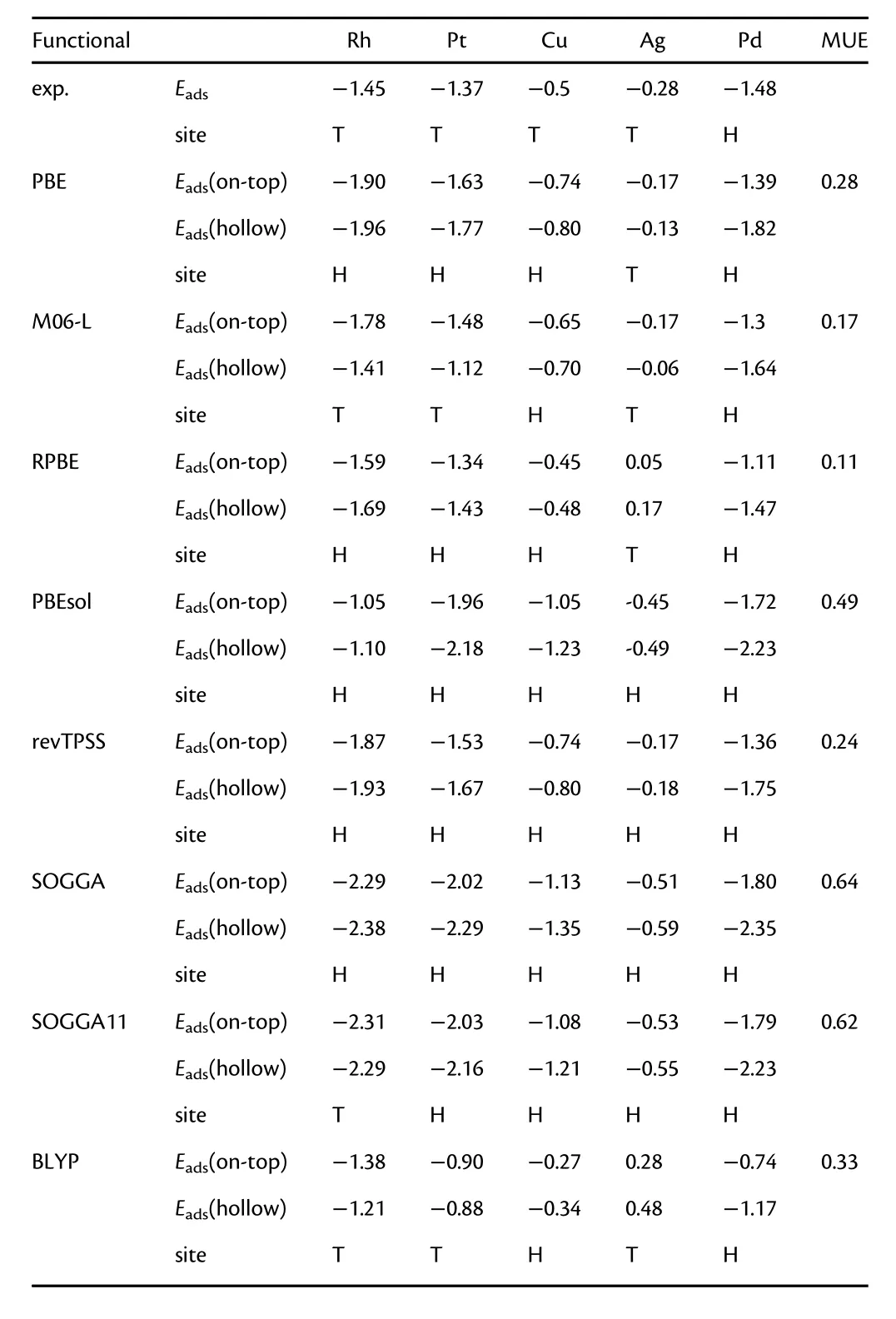
Table 3.The CO adsorption energies(eV)and site preferences on five transition metals from eight density functionals compared to the experiment.The results are from Ref.[190].

In 2012,Wellendorff et al.[108]developed a vdW functional,BEEF-vdW,for surface science by combining the GGA[191]with a nonlocal vdW functional using regularization and cross-validation methods from machine learning.Later,they re fined the mBEEF[192]model by combining an optimized meta-GGA exchange with the PBEsol correlation functional.Their assessments show that mBEEF performs slightly better than BEEF-vdW for the CO puzzle.In 2015,Wellendorff et al.[193]presented an assessment of six functionals(including LDA,PBE,PBEsol,PW91,RPBE,and BEEF-vdW)against a benchmark database containing 39reactions on the transition metal surfaces.Their assessments show that PW91 and PBE overestimate chemisorption energies for the strong covalently bound systems.RPBE performs well for the strongly adsorbed systems,but fails considerably for systems bound by noncovalent interactions.The BEEF-vdW is the best performing functional and provides the same level of accuracy for strong covalent chemisorption and for systems bound with non-covalent interactions.Gautier et al.[194]investigated the chemisorptions of ten molecules(involving ethylene,cyclohexene,benzene,naphthalene,CO,O2,H2,methane,ethane)on Pt(111)using five density functionals(PBE,optPBE-vdW,optB86b-vdW,BEEF-vdW,and PBE-dDsC).Their results show that the optPBE-vdW and PBE-dDsC can provide an overall better prediction of the adsorption energies,[194]and optB86b-vdW is suitable for the description of benzene adsorption on the transition metals surface.It is worth noting that DFT-vdW frameworks trend to overestimate the cohesive energy,because of the attractive nature of the vdW corrections.[195,196]

In summary,from the assessments in the literature,M06-L,BEEF-type functionals,optPBE-vdW,PBE-dDsC,and optB86b-vdW are the promising functionals for predicting the adsorption of molecules on transition metal surfaces,but they are not accurate across the board.One need to quest the functionals that can provide a broadly accurate prediction of adsorptions on different transition metal systems.[194]

3.DFT Descriptors for Electrocatalysts

In this section,we will present several descriptors derived from the DFT calculations for the predictions of the performances of electrocatalysts.

3.1.Formation Energy

The formation energy is a key physical parameter to describe the stability of specific catalysts.The details of the formation energy calculations have been fully reported by Persson et al.,[197]and the formation free energy formula for a compound containing the elements i=1,．．．,n is given as

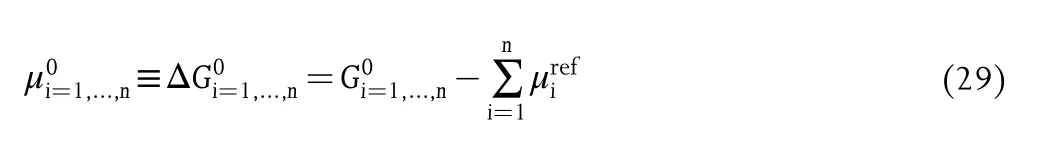
where μ0is the chemical potential, ΔG is the formation free energy,G is the Gibbs free energy of the compound,andis the chemical potential of element i.In principle,a negative value of formation energy indicates a catalyst is energetically favorable,and a positive value suggests the structures are unstable.This equation of formation energy has been widely used to evaluate the stability of target catalysts from the theoretical predictions.[25,92,198-200]

Formation energy is firstly applied to evaluate the likelihood of new catalysts,[198,201]which is usually a necessary precondition for the investigations.[199]If combined with the experimental results,one can deduce the initial guess structures of the catalysts and screen the energetically favorable structures for the catalytic reactions.[202]Meanwhile,formation energies have been employed to guide the design of new catalysts.[25,203-205]

3.2.Adsorption Energy

On basis of the well-known Sabatier principle,[206,207]it is widely accepted that an idea elctrocatalyst should bind adsorbates with an appropriate adsorption strength.A weakly binding interaction may not enable the reaction to be activated.On the other hand,a strong adsorption results in difficulty in conversion and/or desorption of intermediates and final products.The adsorption energy(Eads)can be obtained by using the following equation:

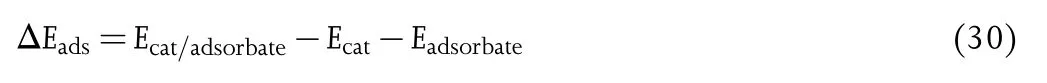
where Ecat/adsorbateis the total energy of the complex formed by catalysts interacting with adsorbates,Ecatis the energy of the electrocatalyst,and Eadsorbateis the energy of the isolated adsorbate.[208-211]The free energy in the form of adsorption energy(ΔGads)is also widely used.[212,213]A negative free energy of adsorption indicates a thermodynamically favorable adsorption,while the positive one reveals an energetically favorable process for desorption.

In general,the suitable range of adsorption energies are variational for different electrocatalytic reactions.For HER,the catalysts with adsorption free energy of hydrogen(ΔG*H)close to zero are considered as the promising candidates.[214-216]The positive ΔG*His detrimental for the adsorption of H on catalytic sites,while a negative ΔG*Hsuppresses the desorption of H2.For OER,the activity is determined by two factors:the difference in adsorption free energies between adsorbed*OOH and*OH,(ΔG*OOH-ΔG*OH),and the relative position of adsorption free energy of adsorbed*O(ΔG*O-ΔG*OH).[217]When ΔG*Olocates at the middle of ΔG*OOHand ΔG*OH,the lowest overpotential is obtained for a specific OER catalyst.[217,218]On the contrary,the correlation of ORR catalytic activity with adsorption free energies is unclear.It is confirmed that the overpotential of ORR is closely related to the adsorption of*OOH or desorption of*OH.[25,198,219]Therefore,the adsorption energy of*OH usually serves as a descriptor in the volcano curve for ORR activity.Furthermore,there is a linear relationship between the adsorption energy of ORR intermediates,[25,198][220]that is,*OOH,*OH,and*O,indicating that the merged volcano curves of adsorption energies of key intermediates can serve as a descriptor for electrocatalytic performance.[198,221]The feature of multiple products of CO2RR demonstrates that the reaction pathway is modulated by several key intermediates.[222]Some studies have shown the reaction pathway is determined by the adsorption energy of*CO.[223-225]For the NRR,there is a transfer of six proton/electron pairs on the NRR process,which involves five main adsorbed species,including,*NNH,*N2H2,*N2H3,*N,*NH,*NH2.Because of the difficulty of activating N2,the catalytic activity of NRR is highly dependent on the*N2H adsorption.[226]Therefore,the adsorption energy of*N2H usually serves as a descriptor in volcano plots to describe the catalytic activity of the NRR catalysts.[227,228]For the aforementioned electrocatalytic reactions,it is convenient to screen high-performance catalysts by calculating adsorption energy of key intermediates.

3.3.Scaling Relations

The scaling relation of adsorption energies between similar adsorbates has already been found in the previous studies,[229-231]and the scaling relation can be used to describe correlation between various reaction species,as shown in the following equation:[232]

where EAand EBrepresent the adsorption energies of species A and B,respectively,and m and b are the slope and intercept of the linear relation,respectively.For a complicated catalytic system,such scaling relations correlate the adsorption energies of most adsorbed species to one or two key intermediates and reduce the degrees of freedom in multistep catalytic reactions,simplifying the understanding of the problem in the interaction of adsorbates-surface.[224,233]The volcano plot can be used for the description of the activity of catalysts,which is expressed as a function of catalytic activity and adsorption energies of key intermediates.[234,235]As shown in Figure 4a,[236]if the reactive species bind too weakly with the catalytic sites,the catalytic process is limited by the adsorption step,whereas if they strongly bind with the catalytic sites,the desorption step is the rate-determining step.

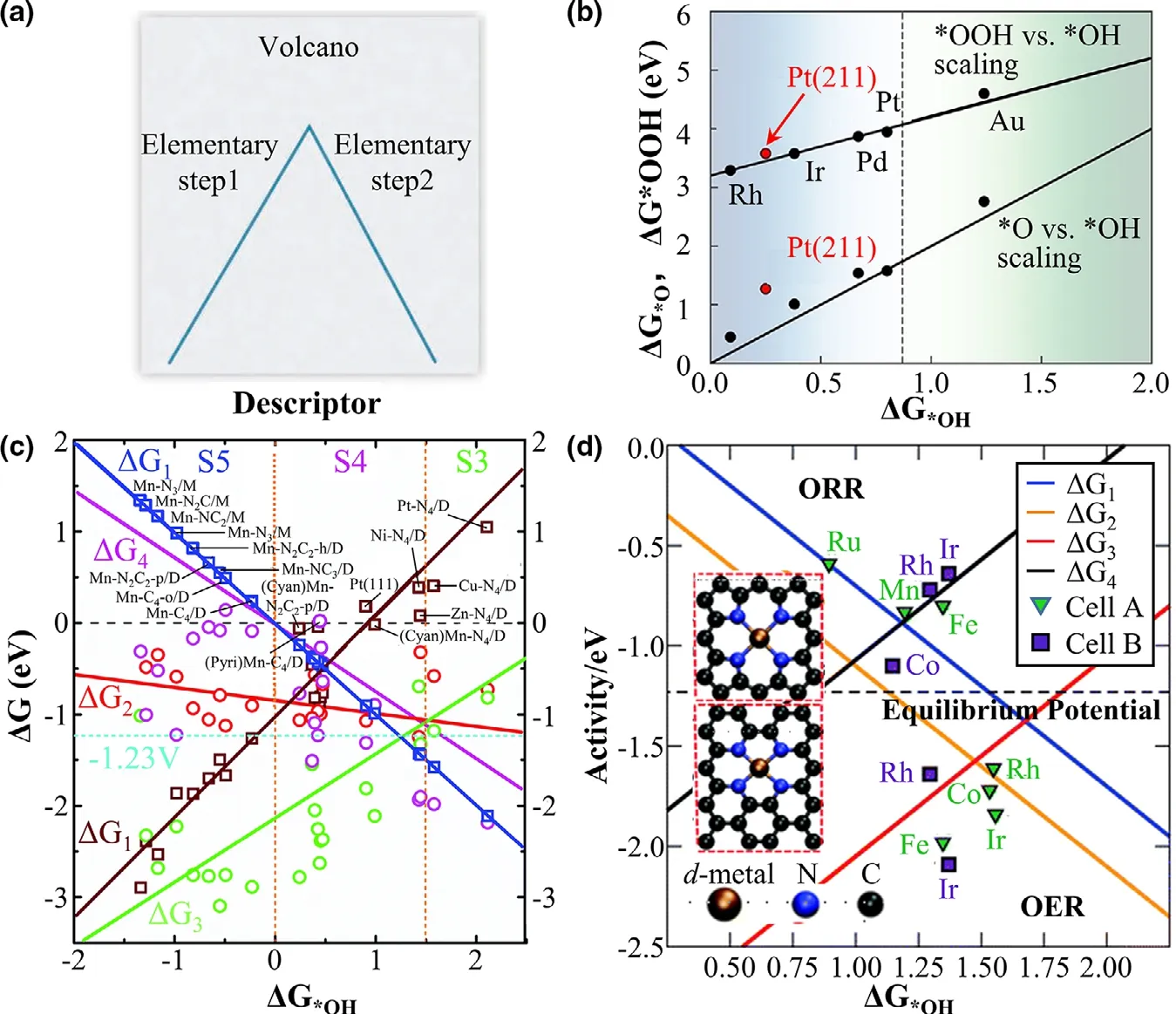
Figure 4.a)Schematic volcano plot for reaction rate.Reprinted with permission from Ref.[236]Copyright 2011,Science.b)Scaling relationships for the chemisorption energies of*OOH and*O for the(111)surface of various metals(black circles)using*OH as a descriptor.Reprinted with permission from Ref.[237]Copyright 2018,American Chemical Society.c)Scaling relation plot for ΔG of each ORR elemental step as a function of ΔG*OH.Reprinted with permission from Ref.[25]Copyright 2019,the Owner Societies.d)Combined volcano plot for the ORR(up)and OER(below).Reprinted with permission from Ref.[219]Copyright 2011,the Owner Societies.

For the ORR,the widely used scaling relations are the relations of ΔG*OOHor ΔG*Ovs ΔG*OH(ΔG denotes the free energy of adsorption).The*OOH vs*OH scaling line generally has a slope close to 1,while the*O vs*OH scaling line has a slope to 2,which is related to the type of bonds formed by O/OH/OOH on electrocatalysts.[237,238]A well-known scaling relation for metal and metal oxides is ΔG*OOH=ΔG*OH+3.2 displayed in Figure 4b.[239]These relations were widely employed in the design of ORR catalysts.[198,201]For instance,Zhu et al.[25]have shown that the five-coordinated(Cyan)Mn-N4/D has an optimum configuration of Mn-Nxstructures with the lowest ORR overpotential(Figure 4c).Furthermore,it is a good strategy to locate the active center in a specific structure with the help of scaling relations(Figure 4d).[219]Combining with experiments,the scaling relations in Figure 5a provide an exploration of the origin of outstanding catalytic performances by the screen of potential active sites.[240,241]Meanwhile,the scaling relations are also well extended to NRR and CO2RR.In Figure 5b,it is obvious that the catalysts with low binding energy to nitrogen impede the conversion of N2to form*N2H,while the rate-determining step is the protonation of*NH to form*NH2or desorption of*NH2to form NH3molecule.[242,243]This provides a strategy of tuning the binding interaction of*N2with the catalyst to boost NRR.For the complicated CO2RR pathways,the scaling relations are usually used to account for the selectivity of products(such as HCOOH,CO,and so on).As shown in the left picture of Figure 5c,the linear relations of CO2→*COOH,*COOH→*CO,*CO→*CHO,and*CHO→*CH2O were established for CO2RR,providing an estimate of overpotential by calculating the difference of the limiting potential ULand the equilibrium potentials.Therefore the CO2→*COOH and CO→*CHO reactions can be used to determine the theoretical overpotential.[224,244]Furthermore,the*CO adsorption energy can act as a descriptor of CO2RR catalytic activity.In general,a low*CO adsorption energy suggests that the rate-determining step is the protonation of CO2to form*COOH,whereas a strong*CO binding to electrocatalysts indicates the protonation of*CO to form *CHO is the ratedetermining step.[245,246]By contrast,the results at the right pane of Figure 5c shows the steps involved in the oxygen-bound intermediates.A weak*OCH3binding strength preferentially leads to the generation of CH3OH,while a high binding strength of*OCH3leads to CH4through breaking the O-CH3bond.[247]

Figure 5.a)ORR and OER volcano plots of overpotential versus adsorption energy of OH*.Reprinted with permission from Ref.[240]Copyright 2016,WILEY-VCH Verlag GmbH&Co.KGaA.b)Activity volcano plot of limiting potential(UL)verse ΔEN*.Reprinted with permission from Ref.[242]Copyright 2019,Elsevier B.V.c)Schematic illustration of the primary protonation steps of CO2RR by predicted limiting potentials(UL)verse EB(*CO)and EB(*OH).Reprinted with permission from Ref.[224]Copyright 2012,American Chemical Society.

The scaling relations can be used for virtual screening of electrocatalysts.[231,238]It has been shown that the environmental change of adsorption induces various responses of adsorbed species,[248-250]which can be used to search for optimal catalysts beyond the scaling relations.The related tactics to go beyond the scaling relations have been developed and summarized in previous works,[251,252],such as the doping of the p-block elements,[229,253-255]the secondary adsorption site,[201,256,257]the proton acceptor groups,[258-260]the alteration of the local environment around catalytic sites,[261,262]and the change of electrolyte composition.[263-265]Lim et al.[266]found that the doping of the p-block element causes an extra stabilization of*COOH via stronger bonding interaction between pzorbital of*COOH and S or As doped Agbased catalysts(Figure 6a),which breaks the scaling relation between*COOH and*CO.This change thus induces a significant decrease of overpotential by 0.4-0.5 V.Shen et al.[267]designed a dual-site cascade ORR mechanism on SnOx/Pt-Cu-Ni catalyst(See Figure 6b).In particular,the*O moiety formed on the SnOxsite transfers to the neighboring Pt site and then keeps on the remaining ORR steps,which reduces the energy barrier for*OOH→*O and improves the catalytic performances.The scaling relations can also be broken by introducing a proton acceptor to stabilize the weakly adsorbed species.As shown in Figure 6c,Gao et al.[268]designed a highly efficient NiO/NiFe layered double hydroxide(LDH)catalyst for OER.The catalytic activity is contributed by the neighboring O sites,as a proton acceptor,facilitating the*OOH dissociation through a weak hydrogen bond interaction.Similarly,for the catalytic systems with too strong or weak adsorption interactions,the grafting of ligands on the surface is also a tactic to change the adsorption states of intermediates and modulate their adsorption properties via extra electrostatic interactions.[269,270]One classic case is the application of strain in the catalysts,it has been proved that the tensile strain shows an effect on increasing binding strength of intermediates,while a compressive strain results in weaker adsorption.[271]The effect of strain on the adsorbed intermediates turns out to be more complex.[272]Xie et al.[261]found that the adsorption of*O was enhanced by applying the tensile strain on nitrogen-doped graphene while leaving the adsorption interactions of*OH and*OOH remain unchanged,therefore breaking the scaling relations.

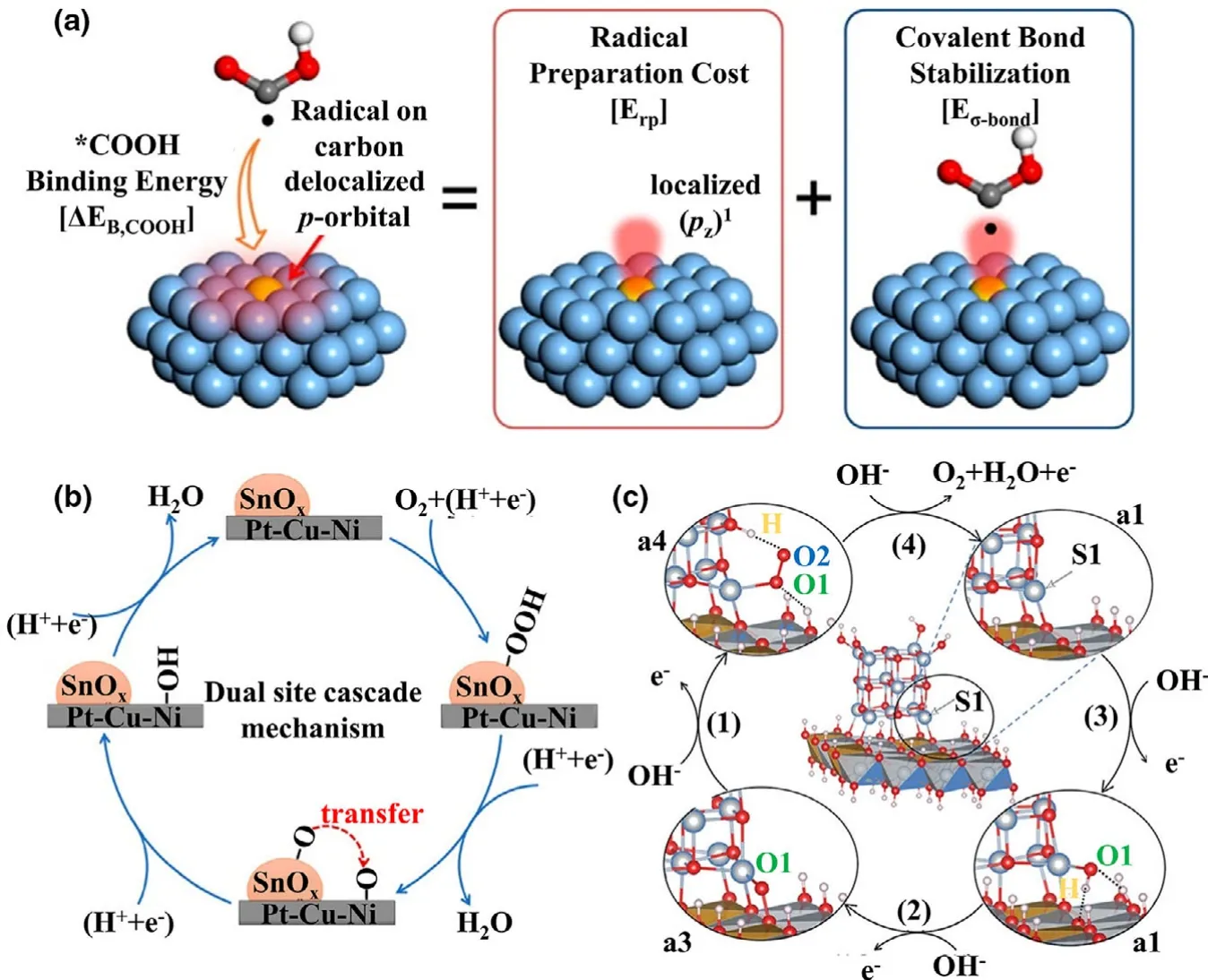
Figure 6.a)Schematic diagram of the COOH binding mechanism on p-block dopants.Reprinted with permission from Ref.[266]Copyright 2014,American Chemical Society.b)Scheme of the dual-site cascade mechanism on SnOx/Pt-Cu-Ni.Reprinted with permission from Ref.[267]Copyright 2019,American Chemical Society.c)Schematic illustration of the OER pathway at S1 site of the NiO/NiFe LDH intersection.Reprinted with permission from Ref.[268]Copyright 2019,Wiley-VCH Verlag GmbH&Co.KGaA.

Some previous works[273-275]have shown that the scaling relations for the lowcoordination sites are not valid,and the solvation effect also impacts the scaling relations.[276]For example,Herron et al.[277]shown that the solvent molecules impede the adsorption of methoxy(CH3O),whereas show minor impact on the binding strength of methanol and hydroxymethyl(CH2OH).Meanwhile,the anions or cations in electrolyte also show significant influences on the adsorption process.For instance,the addition of cations with various sizes,[278]the modifications on the catalytic surface via ions,[264,279,280]and the complexes of ionic liquid and adsorbed species,[281]those strategies associated with electrolyte were able to break the limitation of scaling relations through modifying the adsorption interaction of a specific intermediate.Furthermore,it is worth noting that Doyle et al.[282]proposed spatial confinement that enables the stabilization of*OOH via a nanoscopic channel,while the*OH maintains unaffected.It is a new direction to design efficient catalysts that break the scaling relations.

3.4.d-Band Model

The d-band model theory established by Nørskov and Hammer[288,289]has been successful in describing the trend in the activity of transition metal-based electrocatalysts.In particular,the d-band model demonstrates that the adsorption strength of adsorbates depends on the coupling to the d states of metals.[19,290]For quantifying the effect of the dband on the adsorption interactions,the corresponding d-band center(ϵd)is defined as the local average of the d electron energies:

where x is the energy level and ρ（x）is the density of states of the corresponding d-orbital.Figure 7a shows a clear linear relationship between adsorption energy and the position of d-band center.[19]If the d-band center is close to the Fermi level,the transition metal catalysts are more likely to exhibit higher activity for adsorption.[27,290-292]Generally,the d-band center is governed by two key parameters:the d-band filling and bandwidth.As the number of d electrons increases,the filling level of the d-band rises,and the d-band center will downshift to the lower energy level,which results in a weak adsorption interaction.If the filling level of the band is fixed,a shrunken bandwidth induces a rising level of d-band center and therefore results in a strong adsorption interaction.Consequently,numerous strategies based on the d-band model have been adopted to tune the catalytic activity and to explore the catalytic mechanism of transition metalbased catalysts, including, alloy catalysts,[290,293-295]catalysts with doped species,[296-298]strain,[27,292,299,300]and heterostructure.[301,302]

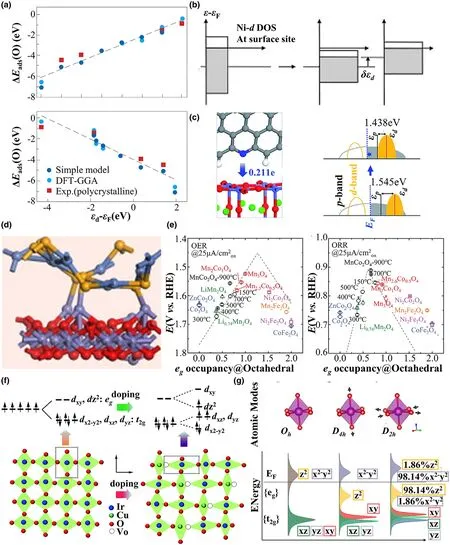
Figure 7.a)Variation in the O adsorption energy,ΔGads(O),on the most close-packed surface of the 4d transition metals.Reprinted with permission from Ref.[19]Copyright 2009,Macmillan Publishers.b)The illustration of the effect of tensile strain on the d-band center.Reprinted with permission from Ref.[283]Copyright 1997,Elsevier Science B.V.c)The charge transfer from 3DNG to PBSCF(left)and the schematic band diagrams of PBSCF and PBSCF with 3DNG(right).Reprinted with permission from Ref.[284]Copyright 2019,The Royal Society of Chemistry.d)The construction of NiSe@Fe2O3heterojunction and model.Reprinted with permission from Ref.[285]Copyright 2020,Elsevier B.V.and Science China Press.e)The OER(left)and ORR(right)volcano plots with the activity as a function of egoccupancy of the active element at octahedral site.Reprinted with permission from Ref.[286]Copyright 2017,WILEY-VCH Verlag GmbH&Co.KGaA.f)Schematic lattice diagram in the ab plane of IrO2(left)and substituted by Cu(right).The top row shows the corresponding Ir-5d orbitals degeneracy of IrO2.Reprinted with permission from Ref.[35]Copyright 2015,The Royal Society of Chemistry.g)Atomic models and corresponding calculated density of states for an isolated MnO6octahedron as a function of increasing deformation.Reprinted with permission from Ref.[287]Copyright 2019,American Chemical Society.

For the alloy catalysts,the d-band center is highly related to the electron transfer originated from the orbital hybridization.[303-305]For example,Wang et al.[306]synthesized a PtGa alloy,which is shown to be a superior HER electrocatalysts.DFT calculations demonstrate that the downshift of d-band center of the outer layer Pt atoms occurs after alloying with Ga.This causes weaker adsorption interaction due to the decrease of electron transfer from the Pt 5d orbital to the adsorbates and boosts the catalytic performances.Besides alloying,the transition metal-derived catalysts,for example,metal sulfides,[307]metal phosphides,[297]metal carbides[298]and single-atom catalysts(SACs)[308]also show adjustable d-band center.[308,309]In addition,the tensile strain can be used to tune the d-band center(Figure 7b).[283]Strasser et al.[292]investigated the Pt-Cu alloy nanoparticles and found that the strain originated from the lattice mismatch between Pt and Cu layers optimizes the Pt d-band states position relative to the Fermi level and results in enhanced ORR performances.

For the heterostructures electrocatalysts,the electron transfers occur at the interfaces of the heterostructures,[302]which can be employed to tune the d-band center.[285]These physical properties can be used to tailor the d-band center of the metal atom and then facilitate the chemisorption of reaction intermediates on the catalytic surface.Bu et al.[284]designed a catalyst,P-3G,a composite of the cation-ordered perovskite(PBSCF)and 3D porous N-doped graphene(3DNG),which exhibits outstanding multifunctional catalytic activities.As displayed in Figure 7c,the high activity of P-3G is attributed to the upshift of the dband center to the Fermi level as a consequence of the electronic transfer from 3DNG to PBSCF.Guo et al.[285]fabricated an outstanding OER catalyst with a core-shell heterogeneous structure(NF/NiSe@Fe2O3).The activity is shown to stem from the tuning d-band center via Fe-Se bond at the interface(Figure 7d).

3.5.egorbital Occupations

Despite its great success,the d-band model fails for transition metal compounds with splitting d-band orbitals,especially for metal oxides,[310]in which the metal coordinated by six identical ligands in octahedral complexes with Ohsymmetry.The d orbitals of the center transition metal atom split into low energy t2gorbitals(dxydxy,dxz,and dyz)and high energy antibonding egorbitals(dx2-y2,dz2).[311,312]The filling state of the egorbitals has been regarded as a descriptor for the activity,which is crucial in governing the binding strength of adsorption/desorption intermediates with catalysts.[313]The calculation of egfilling state is conducted using the well-known formula.[36,311]The catalysts with the medium filling state of egorbitals(eg≈1,namely,the egorbital is occupied by a single electron)usually provide an optimal catalytic activity for OER/ORR(Figure 7e).[286,314]

Based on this descriptor,significant efforts have been made to optimize the catalytic activity of metallic oxides,such as the catalysts with defect,[35]strain,[315]surface reconstruction.[287]Recently, Sun et al.[35]synthesized the copper-doped IrO2catalyst that exhibits better OER activity than pure IrO2.For the pure IrO2,the IrO6nearoctahedral symmetry leaves the electronic configuration of t2g5and eg0of Ir-5d.The low egoccupation hinders the OER process.In the copper-doped IrO2catalyst,Cu0.3Ir0.7Oσ,there is a partial-occupied dz2-antibonding orbital(i.e.,one of eg-antibonding orbitals),promoting the OER catalytic activity(Figure 7f).Zaman et al.adopted the strategy of doping to tune the egoccupation and boost the OER performance.[316]Furthermore,as displayed in Figure 7g,Ignatans et al.[287]found that the mixing of the filled and unfilled egorbitals in the Jahn-Teller distorted LaMnO3facilitates the charge transfer and improves the ORR activity.

In summary,the DFT calculation-derived descriptors can deal with the specific issues that occur in electrocatalysis,such as stability,adsorption strength,and the activity.Furthermore,these descriptors play an important role in the prediction of the performance of electrocatalysts and exploration of the catalytic mechanisms.

4.Tools for Theoretical Analysis

In this section,we will present some tools for the theoretical analysis of the electronic structure of catalysts and the mechanisms of the catalytic reactions.

4.1.Bader Charge

Atomic charges can reveal the bonding environment and charge population of catalytic sites,and shed lights to the mechanisms of the electrocatalysis.The popular charge population analyses are Bader charge,[317]Mulliken charge,[318]Hirshfeld charge,[319]and Voronoi Deformation Density(VDD charge),[320]which are based on different algorithms for partitioning electronic charges to atoms.The Bader charge has been widely employed for the analysis of charge distribution for electrocatalysts.We will focus on some representative works and provide brief introduction of the application of Bader charge analysis in electrocatalysts.

Wu et al.[321]reported that the graphyne demonstrates considerable activity for ORR due to the positively charged carbon atoms(Figure 8a),which acts as the active sites for the adsorption of O2and*OOH and facilitates ORR processes.Zhu et al.[328]synthesized novel Co-Ni3N nanowires,which has much better HER and OER catalytic performance than pure Ni3N nanorods,and the performance enhancement originates from the interface charge transfer.This effect is verified by the XPS spectra and the DFT calculated Bader charges.In addition,electron transfers occur during the adsorption of reaction species(Figure 8b),which activates the reactant and proceeds with the electrocatalytic reaction.Therefore,the number of transferred electrons to adsorbed species increases with the stretched bond length(Figure 8c),[323,329]which can serve as a descriptor for catalytic activity.

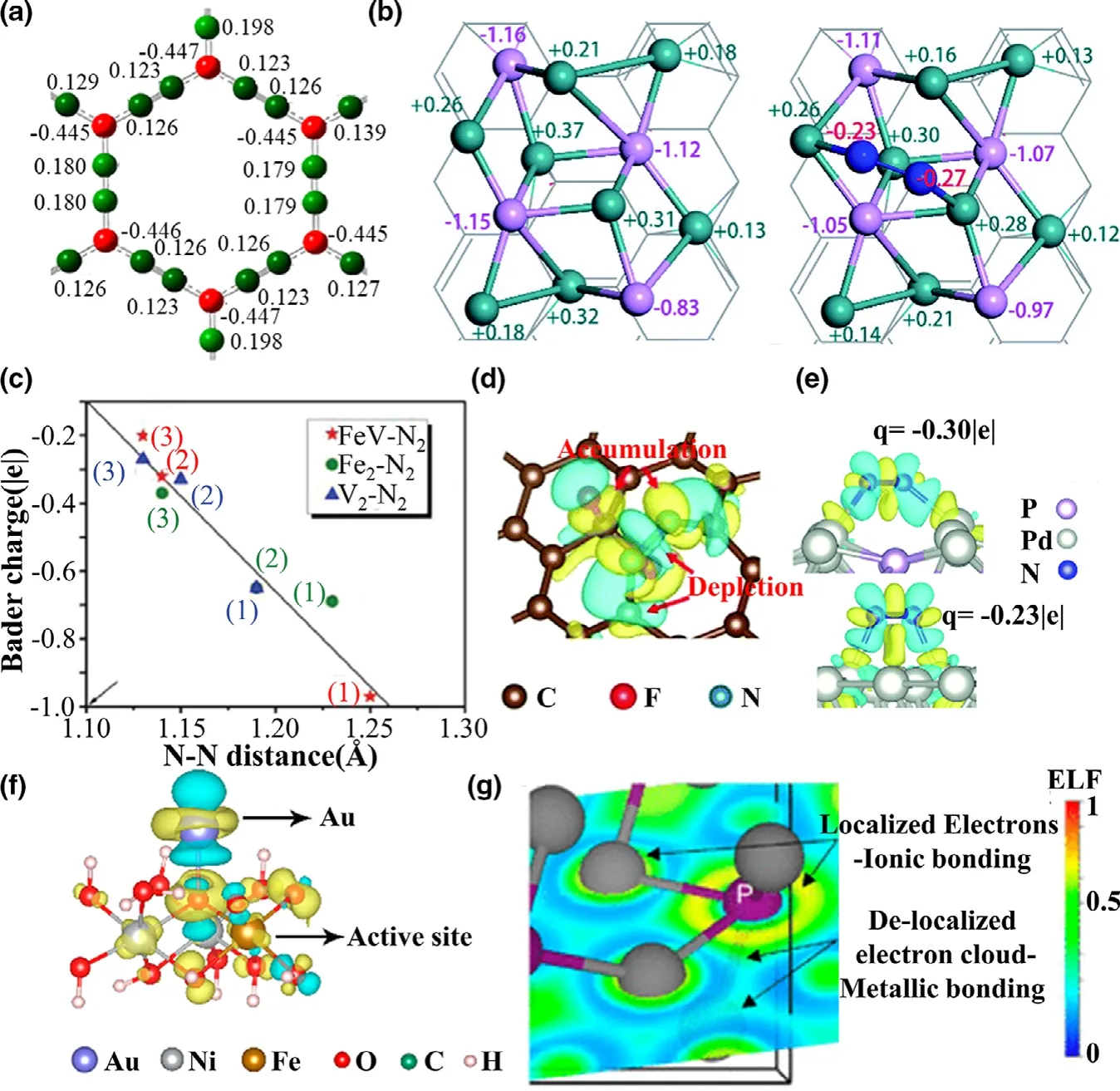
Figure 8.a)Calculated charge distribution on each carbon atom graphene sheet.The red and green colors represent negative and positive charges,respectively.Reprinted with permission from Ref.[321]Copyright 2012,American Chemical Society.b)Optimized geometries and Bader charge results(left)before and(right)after N2adsorption on Ru2P-rGO.Reprinted with permission from Ref.[322]Copyright 2020,The Royal Society of Chemistry.c)Relationship between Bader charges of adsorbed N2 and N single bond and N bond lengths.Reprinted with permission from Ref.[323]Copyright 2020,Elsevier B.V.and Science Press.d)Charge density difference of N2molecules adsorbed on the FC surface.Reprinted with permission from Ref.[324]Copyright 2019,The Royal Society of Chemistry.e)The differential charge density of PdP2(above)and Pd(below)with the adsorption of N2.Yellow and cyan regions represent positive and negative charges,respectively.Reprinted with permission from Ref.[325]Copyright 2019,The Royal Society of Chemistry.f)Differential charge densities of NiFe LDH with and without Au atom when one O atom is adsorbed on the Fe site.Reprinted with permission from Ref.[326]Copyright 2018,American Chemical Society.g)Electron localization function for a plane coincident with two Ni-P bonds.The heat map indicates “localized electrons”in red(ELF ≈ 1)and“delocalized electrons”in green(ELF=0.5)(ELF=0 in blue).Reprinted with permission from Ref.[327]Copyright 2018,American Chemical Society.

4.2.Difference of Charge Density

The difference of charge density is the result of the charge transfer between the electrocatalyst and intermediates via bonding interactions.The strength of the bond depends on the amount of electron transfer,which primarily determines the catalytic kinetics related to adsorption and desorption of intermediates.Therefore,it is not surprising that the difference of charge density analysis becomes popular in the exploration of the electronic transferring process during a catalytic reaction.Yuan et al.[324]reported that the fluorine-doped carbon can serve as an NRR catalyst with an enhanced NRR activity.The DFT calculated charge density difference in Figure 8d shows that the charge transfers occur from the N2molecule to the adjacent C and F atoms.Meanwhile,the electron density of the C and F atoms can donate back to the π*orbitals of the N2molecule,resulting in the weakening of the N-N bond and strengthening of the binding of N2on the electrocatalytic site.In the case of a novel PdP2catalyst for NRR,[325]the charge density difference coupled with Bader charge analysis shows that the charge transfer on the PdP2surface is much greater than that on the Pd surface,unveiling the highly active sites on the PdP2surface and the enhanced NRR catalytic performances(Figure 8e).

The activity of an electrocatalyst is closely related to its electronic structures,and it is necessary to study the role of various modifications in electronic structure,which can broaden the horizon for improving catalytic activity.Zhang et al.[326]synthesized single-atom Au supported on NiFe LDH with a sixfold OER activity enhancement.As displayed in Figure 8f,the high activity is attributed to the hybridization of Au-dz2 orbital and O-pzorbitals,inducing the electronic transfer to s-urrounding O,Ni,and Fe atoms,which facilitates the adsorption of OH and lowers the overpotential.

4.3.Electron Localization Function(ELF)

ELF is a measure of the likelihood of finding an electron in the neighborhood,[330,331]which may reveal the type of bonding interactions:for example,metallic,ionic,and covalent bonds.[332]In general,ELF is a position-dependent function ranging from 0 to 1 which is represented by different electron localization.The ELF value close to 0.0 indicates the ionic bond feature with completely delocalized electrons,a value of 0.5 represents the metallic bond with electron gas-like behavior,and a value of 1.0 represents the covalent bond with complete electron localization character.Laursen et al.[327]reported a noble-metal-free electrocatalyst,Ni3P,with high efficiency for HER.Their DFT calculations revealed that most of the space around the Ni-P bonds shows an ELF value of about 0.46(Figure 8g),indicating a delocalized electron cloud consistent with the metallic bond.The high electron conductivity benefits the electrocatalytic activity of HER.[333]

Meanwhile,ELF can be adopted to estimate the interacting configurations.For instance,Gao et al.[333]disclosed the selectivity of N2adsorption configuration through ELF.They found that the electron lone-pair of N2is easy to participate in the bonding process via the end-on configuration,resulting in greater adsorption energy than that in side-on mode.Furthermore,ELF can be employed to show the type and strength of the chemical bond between adsorbed species and the catalytic surface.[334]

4.4.Density of States

One useful tool for the orbital analysis of solids is the density of states(DOS),which can give an in-depth understanding of the orbital interactions.It is generally recognized that the electronic states crossing the Fermi level without a band gap reveal the metallic conductive behaviors of catalysts,while the presence of a band gap at the Fermi level confirms the semiconductive or insulator property.[335-337]The DOS near the Fermi level can directly reflect the capability of the electron evolution or transfer on the catalyst surface.[271,338]Moreover,the abundant states near the Fermi level may indicate the high activity of the catalysts.[339]For instance,Lu et al.[340]investigated the sulfurdoped graphene for ORR by the DOS analysis.As shown in Figure 9a,the emerged peaks in the DOS profile mainly come from the sulfur dopant and its neighboring C atom,indicating that the enhanced activity stemmed from S-doping.Notably,the popular usage of DOS is to locate the d-band center,which can evaluate the catalytic activities of transition metal-based catalysts.[297,308,309]Besides the orbital symmetry,the matching of the energy level is the prerequisite of chemisorption and the catalytic reactions(Figure 9b).[341]After the adsorption,a covalent bond formed,evidenced by the presence of two resonance mixed orbitals of adsorbed species and active sites.The bonding orbital at a low energy level is mainly composed of s/pcomponent of adsorbates,while the high energy one is the antibonding orbital mostly consisted of p/d-component of the active center(Figure 9c).Furthermore,the difference in the adsorption strength can originate from the antibonding states.The higher location of the highest peak of active center DOS(Ep),the antibonding states move higher with lower occupancy,resulting in a stronger interaction between adsorbate and catalyst surface(Figure 9d).[342,343]

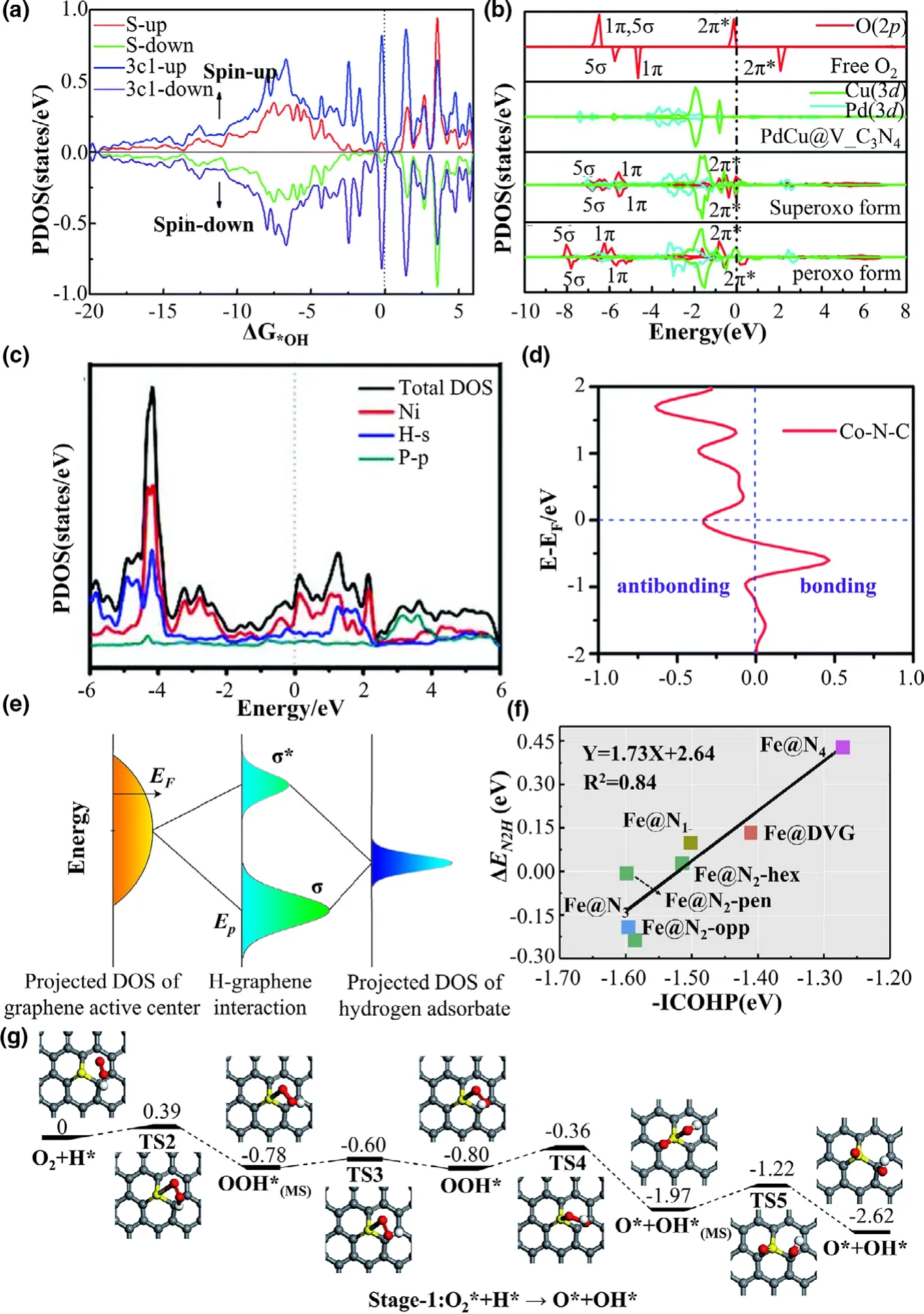
Figure 9.a)The projected density of states(PDOS)for S and three “C1”atoms of SGV.Reprinted with permission from Ref.[340]Copyright 2017,The Royal Society of Chemistry.b)The corresponding PDOS plots for O2on PdCu@V_C3N4for side-on and end-on configurations.Reprinted with permission from Ref.[341]Copyright 2020,The Royal Society of Chemistry.c)Total and projected densities of states(TDOS and PDOS)calculated for Ni12P5.Reprinted with permission from Ref.[212]Copyright 2019,The Royal Society of Chemistry.d)Energy level diagram showing orbital hybridization of active sites and hydrogen adsorbate.EFis the Fermi level of the substrate;σ and σ*indicate bonding and antibonding states,respectively.Reprinted with permission from Ref.[358]Copyright 2016,Macmillan Publishers Limited.e)Calculated-ICOHP versus ΔEfor*N2H adsorbed on Fe@Nx.Reprinted with permission from Ref.[242]Copyright 2019,Elsevier B.V.f)Bonding-antibonding property of the M-N bond reflected by the COHP for M-N4systems.Reprinted with permission from Ref.[359]Copyright 2020,The Royal Society of Chemistry.g)Schematic potential energy profiles for the formation of OOH*and the direct dissociation of OOH*on SGV.The calculated transition and metastable state states are denoted as TS and MS,respectively.Reprinted with permission from Ref.[340]Copyright 2017,The Royal Society of Chemistry.

The orbital interactions between adsorbates and catalysts can be further investigated by using the projected density of states(PDOS).The intrinsic interactions can be revealed by the couplings of the molecular orbitals in adsorbates and those in electrocatalysts.The typical examples are the catalytic reactions in OER and ORR,[344,345]involving absorbed oxygen species.The O2molecule has the triplet state(↑O=O↑)with one pair of σ/σ*consisted of pzorbitals and one pair π/π*consisted of pxand pyorbitals in the molecular orbital.This naturally leads to adsorption interaction of O2molecule on the metal active sites via the interaction of the bonding d-p(π and σ)orbitals,and the PDOS of the π orbital is located at the energy level near the Fermi level(the DOS of σ orbital is at the lower energy level).[346-348]For the*OH and*OOH species,the introduction of H 1s orbital results in the hybridization of p-s,for example,the hybridization of pz+s of*OH.When OH is adsorbed on the transition metal sites via the on-top configuration,the bonding interactions include the π orbitals formed by TM(dxz,dyz)and OH(px,py)and σ orbital formed by TM(dz2)and OH(pz+s).[349]Significantly,the strength of these interactions can be directly revealed by the energy level of the group orbitals in PDOS.The relation between the PDOS results and the adsorption interaction of the adsorbates and catalysts can be correlated by the parallel comparison of the energy level of the bonding orbitals.[344]This relation is also found at the PDOS for catalytic reactions relate to the C[350-352]and N[353-357]species(it is worth noting that the σ(pz+s)orbitals of the P,N,C species located at the higher energy level than the π(px,py)orbitals).

4.5.Crystal Overlap Hamiltonian Population(COHP)

The crystal orbital Hamilton population(COHP)and the crystal orbital overlap population (COOP)analysis[352,360,361]are useful tools to extract chemical bonding information out of the calculated electron density,for example,bonding and antibonding characteristics of the electronic states.[362-364]

For a diatomic molecule,for example,H··H,the electronic structure can be accurately described as a linear combination of normalized atomic orbitals(LCAO):

where χ1and χ2are the 1s hydrogen atomic orbitals(AO)centered on two isolated hydrogen atoms 1 and 2.c1and c2denote the amplitude of the electron densities on proton 1 or proton 2.The molecular orbital(MO)is occupied by 2 electrons,and the electronic population is normalized to be 1:

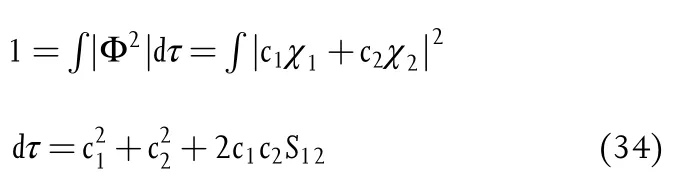
where S12is the overlap integral,indicating the strength of covalent bonding between the two hydrogen atoms.[318]According to the LCAO-MO theory,[365]the positive and negative overlap populations are defined as the attractions(bonding)and repulsions(antibonding),respectively.

Inspired by the overlap populations,the crystal orbital Hamilton population(COHP)analysis can be used as a quantitative measure of bonding strength for the molecular and/or solid systems.[366]Based on the COHP diagram,one can identify bonding,nonbonding,and antibonding regions.In addition,the energy-resolved visualization of chemical bonding interactions in the systems can also be obtained through COHP based on DFT calculations.[362,367,368]For the chemical bonding interactions of two adjacent atoms,the filling of the antibonding state below the Fermi level lowers the bonding strength[369]and the downshifting of occupied antibonding states destabilizes the chemical bonds.[370,371]Furthermore,the positive COHP values around the Fermi level indicate a strong electrondonating ability of the active sites,which can accelerate the electron transfer between adsorbates and catalysts during the catalytic reactions(Figure 9e),such as in ORR.[359]As a quantitative indicator,the integrated COHP(ICOHP)is obtained by integrating the energy up to the Fermi level.In general,the less negative the ICOHP,the larger the binding strength(Figure 9f).[242]Therefore,COHP is a useful tool to decipher the bonding nature in electrocatalysis,which provides the basis for the development of new and efficient catalysts.

4.6.Transition State Theory(TST)

A saddle point(transition state)on the potential energy surface(PES)corresponds to a maximum along a minimum energy path(MEP).[372]The frequently applied algorithms for the transition state searching can be broadly classified into two major categories.The first group is the methods based on the initial guess of transition states,for example,the direct inversion in the iterative subspace(DIIS),[373]geometry direct inversion in the iterative subspace algorithm(GDIIS),[374]and the Berny algorithm.[375]The second group is the method based on the optimized reactant and product structures,for example,the popular linear synchronous transit(LST)/quadratic synchronous transit(QST)method in the DMol3 code,[376]and climbing image nudged elastic band method(CI-NEB)complemented in the VASP code.[377]

By comparing the barrier heights for different reaction pathways,one can find the mechanism of the electrocatalytic reaction.[378-381]Taking the formation of*O and*OH on S-doped graphene as example(Figure 9g),[340]DFT calculations have shown that the first step is the co-adsorption of*O2and*H.Subsequently,the*H moieties approached*O2to form the metastable state of*OOH on the S site.Afterward,the adsorbed*OOH is dissociated into co-adsorption of*O+*OH species and they move to a proper site to form the most stable configuration.

In summary,the above-mentioned theoretical tools facilitate the understanding of catalytic mechanism and guiding the design of highly efficient electrocatalysts.

5.Electrocatalytic reactions

The computational methodology for the treatment of electrocatalytic reactions within DFT is important for exploring the catalytic mechanism.The pH-and potential-dependent free energy can be calculated through the following scheme developed by Nørskov:[382]

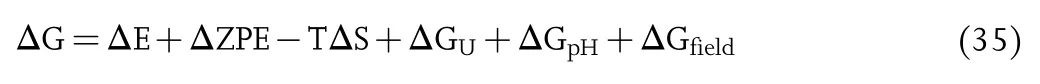
where ΔE is the energy of reaction,ZPE is the vibrational zero-point energy,T is the temperature,ΔS is the entropy.The computations of ZPE and S require the vibrational frequencies calculated by DFT.In order to reduce the computational cost,only the vibrational modes related to the adsorption are computed explicitly.ΔGUand ΔGpHare the free energy contributions due to variations in the electrode potential U and pH,respectively.Note that-ΔGU=neU,where n is the number of electrons transferred and U is the applied electrode potential vs.the standard hydrogen electrode(SHE).ΔGpH=-kBTln(H+)=pH×kBTln10,where kBis the Boltzmann constant.ΔGfieldis the correction of the free energy from the electrochemical double layer,which has been shown to be small and can be neglected according to previous studies.[383]Under the condition of 1 bar of H2,an electrode potential of U=0 vs.SHE,and pH=0,the reaction H++e-=1/2H2is in equilibrium at 298 K.According to the computational hydrogen electrode(CHE)model developed by Nørskov and coworkers,[382]by setting the reference potential to be that of the standard hydrogen electrode,the free energy of 1/2H2can be used in place of the chemical potential for the H+/epair.Since the gas phase H2O was in equilibrium with liquid water at 300 K with a pressure of 0.035 bar,the free energy of H2O was equal to that of the gas phase at 300 K.The free energy of the O2molecule can be calculated from the reaction O2+2H2=2H2O for which the free energy change is 4.92 eV.

From this scheme,if the number of electrons transferred in a catalytic reaction is one,the obtained ΔG(in units of eV)is equal to the reaction potential ULbased on the equation of-ΔG/ne=UL.And the deviation of the reaction potential ULand equilibrium potential E0determines the theoretical overpotential η.The larger the deviation,the larger the overpotential.For a catalytic reaction involved with a multi-electron transfer,for example,ORR,a step for each electron transfer is regarded as an elemental reaction,which can generate a potential deviation relative to the equilibrium potential.The theoretical overpotential η can be calculated by the maximal deviation,and the corresponding step is known as the rate-determining step(RDS).In the case of an ideal catalyst,the overpotential η is identical to 0.Therefore,the design of efficient catalysts aims to the free energy of each step close to the equilibrium potential with the optimal catalytic activity.

5.1.Hydrogen Evolution Reaction(HER)

It is a promising sustainable technology to produce hydrogen(H2)molecules from electrocatalysis powered by renewable sources of energy.Hydrogen evolution reaction(HER)has attracted tremendous attention.HER is a two-electron transfer catalytic reaction involving one intermediate*H.The possible reaction pathway that occurs in an acid medium is either the Volmer-Heyrovsky or Volmer-Tafel reaction mechanism as illustrated in the following equations:[388,389]

The Volmer step(Eq.36)is the adsorption of protons on the surface of electrocatalysts to form H*,followed by either the Tafel recombination step or the Heyrovsky step.In the Tafel step,the H*moiety couples with the adjacent H*to yield H2,and desorbed from the active sites(Figure 10a).Since HER is a 2e-transfer reaction,both the Volmer step and the Heyrovsky/Tafel step determine the HER activity,and the hydrogen adsorption energy(ΔGH*)is a dominant factor for the overall HER process,which can be applied to describe the HER activity.ΔGH*=0 is optimal for HER catalysts.As depicted in Figure 10a,b negative ΔGH*shows a strong binding of H to the catalytic surface,indicating that the desorption(Heyrovsky/Tafel)step limits the HER kinetics;whereas a positive ΔGH*reflects weak adsorption of hydrogen,suggesting that the rate-determining step is the adsorption(Volmer)step.[385]As a result of the adsorption energy ΔGH*on Pt surface approaching 0,Pt and Pt-based catalysts have been regarded as one of the best catalysts toward HER.[390]However,its scarcity and high cost hinder the large-scale application of Pt-based catalysts,many researchers are developing low-cost and high-performance alternatives.

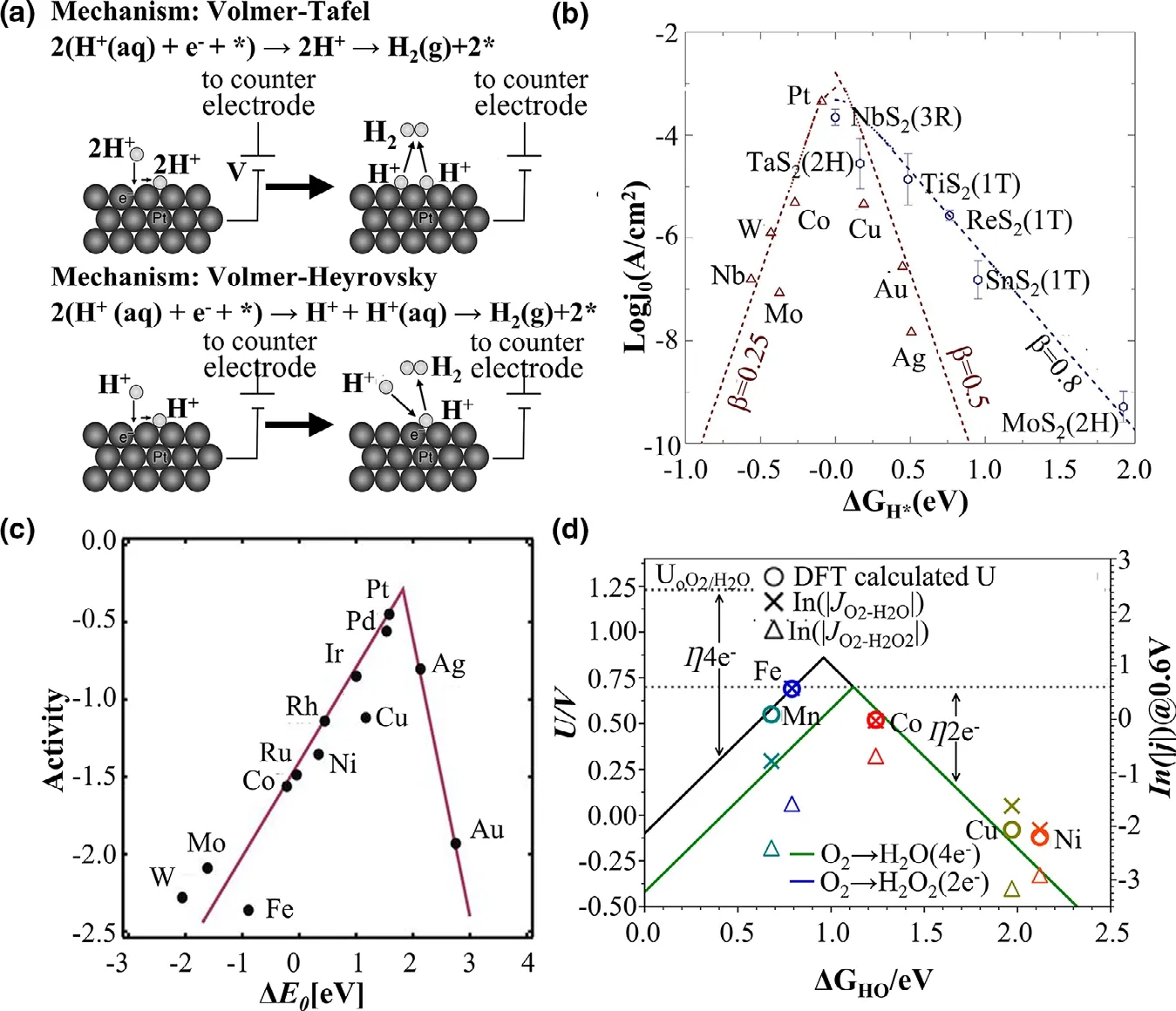
Figure 10.a)Two mechanisms for the HER reaction:the Volmer-Tafel mechanism and the Volmer-Heyrovsky.Reprinted with permission from Ref.[384]Copyright 2012,The American Chemical Society and Division of Chemical Education,Inc.b)Volcano plot of the exchange current density verse the free energy of adsorbed H.Reprinted with permission from Ref.[385]Copyright 2019,Elsevier Ltd.c)ORR volcano plot for metals.Reprinted with permission from Ref.[386]Copyright 2004,American Chemical Society.d)Volcano plots for the two-(green so1lid line)and four-electron ORR(black solid line).Reprinted with permission from Ref.[387]Copyright 2019,American Chemical Society.

In recent years,MoS2is recognized as the most promising alternative to Pt catalysts due to its affordability and its suitable ΔGH*(close to zero).[7]Recently,DFT calculations showed that the Mo edge plane of MoS2is the most active site,with ΔGH*=0.08 eV.The sites on the basal plane of MoS2,have ΔGH*about 1.8 eV,[391,392]and this was confirmed experimentally in a recent report.[393]It has been found that the catalytic performance of a single layer MoS2deposited on Au(110)is proportional to the length of the MoS2,and some strategies have been adapted to expose active planes to further enhance catalytic performance,such as three-dimensional mesoporous MoS2nanostructure,[394]MoS2@conductive-supports,[395]and 1T’-MoS2structure transformed from 2H-MoS2.[396]The catalytic activity of 1T’-MoS2has been investigated by DFT calculations,and the results show that both the basal plane and Mo edge of 1T’-MoS2are active sites with ΔGH*=0.06 and-0.03 eV,respectively,and the catalytic performance of 1T’-MoS2is better than that of 2H-MoS2.[397]

5.2.Oxygen Reduction Reaction(ORR)and Oxygen Evolution Reaction(OER)

The polymer electrolyte fuel cells(PEFCs)are considered as the clean alternative power supply for vehicles and transport applications due to their high power density and low operating temperature.As the half-reaction at the cathode,due to its multistep reaction with slow sluggish kinetics,the oxygen reduction reaction(ORR)hinders the practical large-scale application of PEFCs.[398]A deep insight of the catalytic mechanism is crucial to accelerate the development of ORR catalysts.

In ORR,O2is reduced to form H2O,and involving three intermediates,oxygen(O*),hydroxyl (OH*), and super hydroxyl(OOH*).ORR usually proceeds with the dissociative or associative reaction pathways:[382]

Dissociative:

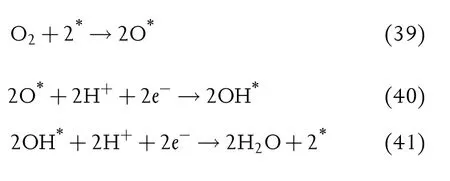
Associative:

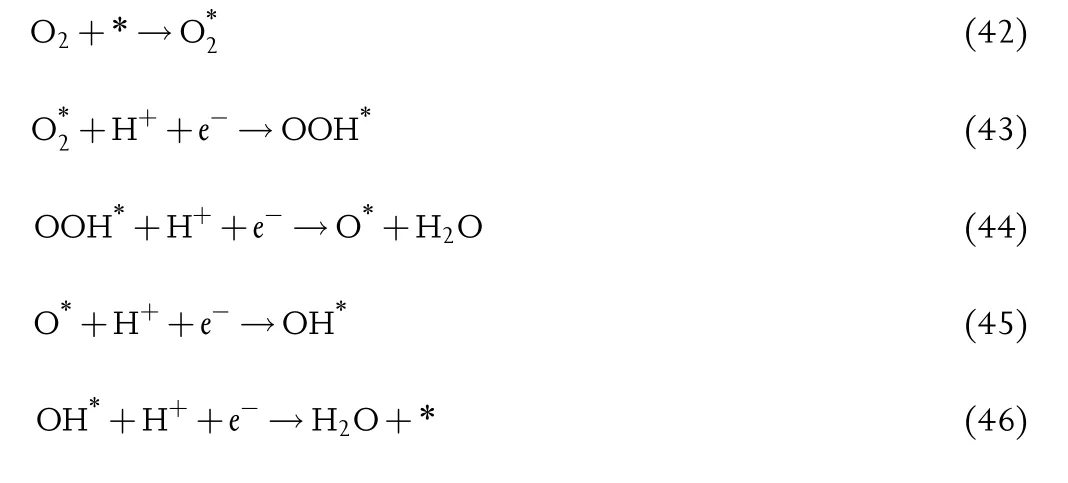
For the ORR multistep electron transfer process,the adsorption strength of oxygen-containing species plays a vital role in the catalytic activity.Furthermore,due to the aforementioned scaling relation,[237]the catalytic activity is usually shown to be determined by the binding strength of one adsorbed species,which was displayed in a volcano plot(e.g.,Figure 10c).[382]Typically,metals that bind intermediates strongly locate at the left branch of the volcano plot,and the ratedetermining step for these metals is the protonation of*O or*OH.For the metals that bind oxygen weakly,they locate at the right branch of the volcano plot,and the proton-electron transfer to O2*(associative mechanism)or the splitting of the O-O bond in O2(dissociative mechanism)are the rate-determining steps.Note that Pt is near the top of the volcano,which has been well-supported by many experimental studies.[399]Nevertheless,the scarcity and high cost of Pt limits its commercial applications in PEFCs.

For the ORR reaction,the hydrogen peroxide production is a competitive reaction,which can convert O2to H2O2involving the intermediate(*OOH)with two-electron transfer process as(Figure 10d):[333]

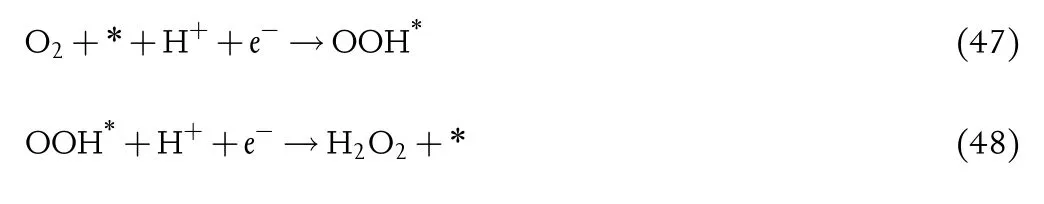
The two-electron transfer processes are similar to HER,the adsorption of*OOH mainly determines the catalytic activity.When ΔGOOH*approaches to a suitable value,the*OOH binds to the surface neither strongly nor weakly,leading to an optimal catalytic activity.Meanwhile,since*OOH is also an intermediate of ORR,if*OOH binds the surface strongly,the four-electron ORR reaction route will dominate the catalytic process.However,the volcano plots of the both are overlapped for the same rate-determining step when*OOH binds weakly.[404,405]

As the inverse process of ORR reaction,the OER reaction produces the O2molecule from H2O involving the same electron transfer and intermediates(*OOH,*OH,and*O).Theoretically,the difference in Gibbs free energies between*OOH and*OH(ΔΔG= ΔG*OOH--ΔG*OH)is 2.46 eV,and the difference in Gibbs free energies between*O and*OH(ΔG*O-ΔG*OH)is1.23 eV for ideal OER catalyst,resulting in the overpotential of 0 V.Actually,due to the limitation of the scaling relation,[382]ΔΔG is typically approximate constant of 3.2 eV for metal oxides,and the ηOERis almost solely dependent on(ΔG*O-ΔG*OH)alone.[217]Therefore,OER activity can be described as ΔG*O-ΔG*OH,and the best activity occurs near 1.6 eV(Figure 11a).[400]When the difference of chemical adsorption energy between O*and OH*is too large,such as ΔG*O-ΔG*OH＞＞1.6 eV,it will bring the high overpotential in the process of desorbing O intermediate,while will need high overpotential to desorb OH intermediate if ΔG*O-ΔG*OH＜＜1.6 eV.

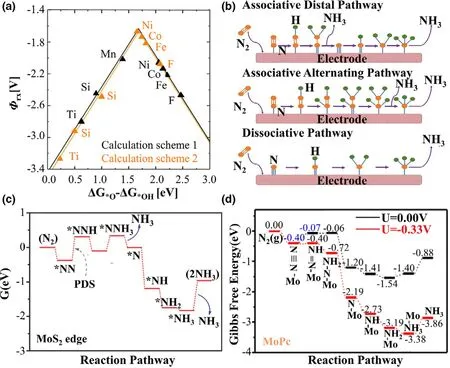
Figure 11.a)The negative of the reaction potentials(-φrx)versus the binding energy differences of ΔG*O-ΔG*OH.Reprinted with permission from Ref.[400]Copyright 2012,American Chemical Society.b)Possible reaction pathways of NRR on metal-based heterogeneous electrocatalysts.Reprinted with permission from Ref.[401]Copyright 2018,The Royal Society of Chemistry.c)Free-energy profile for NRR at MoS2edge site.Reprinted with permission from Ref.[402]Copyright 2018,WILEY-VCH Verlag GmbH&Co.KGaA.d)Calculated free energy profile in NRR on the MoPc catalyst.Reprinted with permission from Ref.[403]Copyright 2020,American Chemical Society.

5.3.Nitrogen Reduction Reaction

The traditional Haber-Bosch process for nitrogen reduction is of high energy demand with enormous CO2emissions,the electrochemical N2reduction reaction is a potential clean alternative technology.Many researchers have conducted DFT calculations to investigate the electrochemical NRR mechanism. For instance,Yang et al.performed the DFT highthroughput screening of catalysts for NRR among a series of transition metal atoms supported on phthalocyanine or borophene monolayer,which provided insights to rational design and explore the efficient and stable NRR catalysts.[403,406]In particular,the NRR reaction(N2+6H++6e-→2NH3)involves several intermediates(*N2H,*N2H2,*N2H3,*NH2,and*N)with two potential reaction pathways(Figure 11b).One is the dissociative pathway,in which the first step is N2dissociates into two separate N atoms before the hydrogenation.The other one is the associative pathway,converting N2to NH3by consecutive proton-coupled electron transfer reactions.

Based on the scaling relation(Figure 5b),a volcano plot was built to understand the rate-determining step on various catalysts by correlating the theoretical overpotential to ΔE*N.[242]It has been proposed that the first protonation of*N2to from*N2H is the potential limiting step on catalysts with weakly nitrogen-binding capability(Figure 11c),while the most difficult step is suggested to be the reduction of*NH2to NH3or the protonation of*NH to form*NH2on catalysts with strong nitrogen binding(Figure 11d).[367,403,407]Moreover,the HER reaction is a competing reaction,decreasing the faradaic efficiency for NRR.Some studies demonstrated that NRR at more negative potentials(-1 to-1.5 V)will dominate over HER because of stronger nitrogen binding on the active site than that of H.[408]

5.4.Carbon Dioxide Reduction Reaction

Great interest has been focused on the sustainable carbon-cycle utilization of the main greenhouse gas(CO2).The electrocatalytic reduction of CO2(CO2RR)is a promising route that delivers a wide range of products of the CO2RR through complex reaction pathways(Figure 12),[409-412]including C1products(carbon monoxide(CO),formic acid(HCOOH),formaldehyde(HCHO),methanol(CH3OH)and methane (CH4), C2products (ethene (C2H4), acetaldehyde(CH3CHO),ethanol(C2H5OH)and acetic acid(CH3COOH)),and C3products(n-propanol(C3H7OH)).[413,414]Since the presence of the scaling relation in CO2RR intermediates,the selectivity of CO2RR products is mainly determined by the adsorption energy of key intermediates.[415]Taking the metallic catalysts as an example,some of the late transition metals(such as Au,Ag,Zn)tend to adsorb and stabilize*COOH strongly and bind*CO weakly,causing that the main CO2RR reduction product is CO.[416]Other metals(Sn,Pb,Hg,etc.)are in favor of the stabilization of*OCHO rather than*COOH intermediate,resulting in the HCOOH as the main product.[417,418]Note that the Cu metal with feasible binding strength for*COOH and*CO yields various C1-3hydrocarbons as well as alcohols.[419]Furthermore,the adsorption energies of key intermediates tailor the catalytic activity of CO2RR.Generally,the adsorption energies of*CO or*CHO dominate the overall CO2RR catalytic performances.[203,411,420,421]

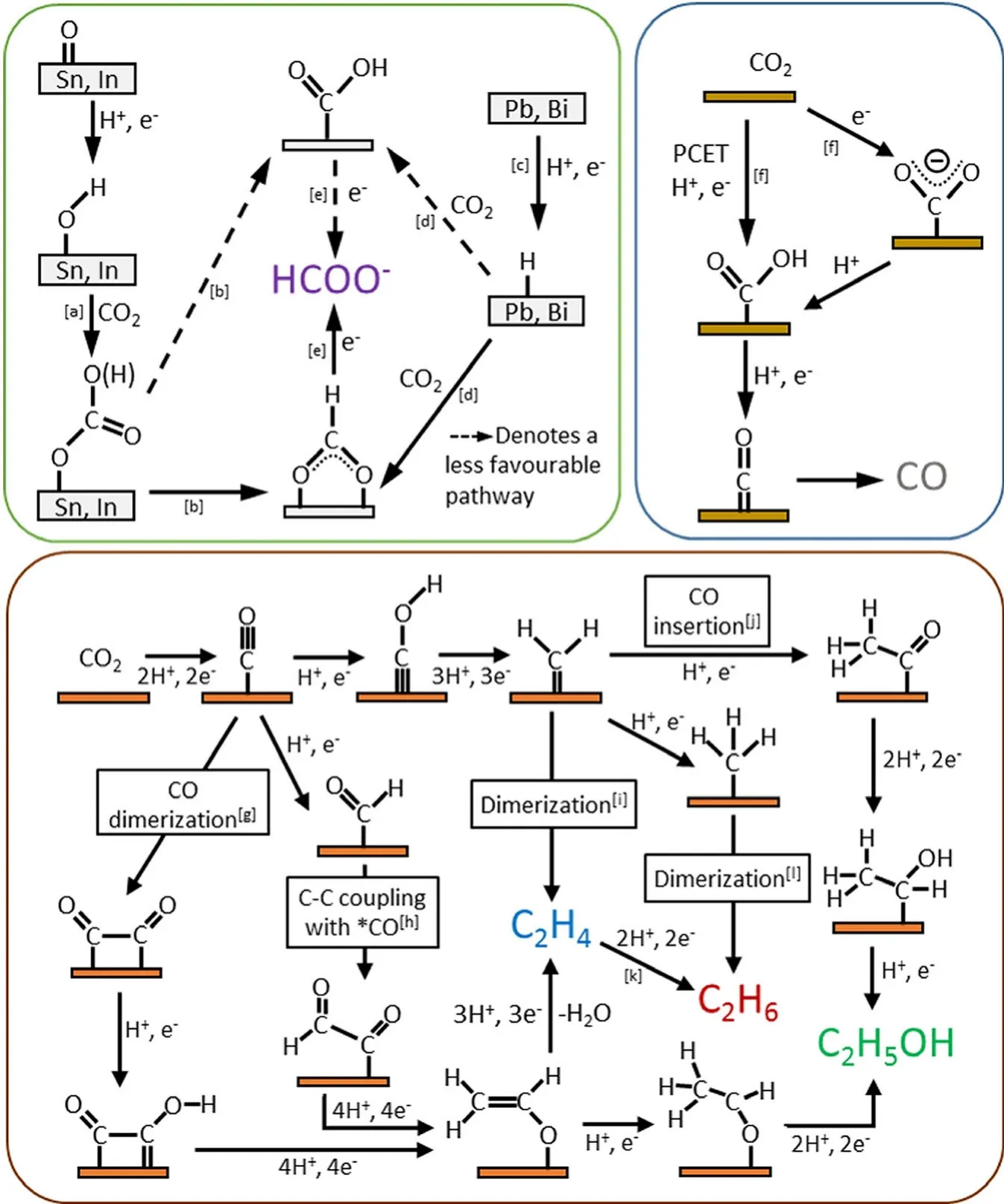
Figure 12.Mechanisms for the reduction of CO2.Reprinted with permission from Ref.[409]Copyright 2018,Elsevier.

6.Perspectives and Outlook

DFT calculations have been widely employed to investigate electrocatalysis for decades,and tremendous progresses have been achieved in developing density functionals to predict the performances of electrocatalysts and to aid the design of highly efficient catalysts.However,density functional approximations are still facing the challenge to accurately predict energetics in complex electrocatalysis.It is a continuous endeavor to develop density functionals which can provide broad accuracy for electrocatalysis and high efficiency for screening of a wider range of potential electrocatalysts.

With a large number of potential non-metal materials (e.g.,doping graphene,[407]g-C3N4,[422]borophene,[423]boron nitride,[424]phosphorene,[425]main-group metals[417])for electrocatalysis, some of the established descriptors of estimating the catalytic activity of transition metal series,such as the d-band model and egorbital occupations,are not suitable for the catalysts composed of main-group elements.Therefore,new descriptors based on DFT calculations for non-metal catalysts should be developed.Recently,Zhou et al.reported that the heterostructures of N-doped graphene supported by MXene monolayers possess highly active ORR and HER bifunctional activities,[426]and the enhanced activities are due to the downshift of the p-band center of carbon atoms(Figure 13a),caused by the interaction of the pzorbital of carbon atoms with the adsorbate.The p-band model has the potential to predict the reactivity of non-metal catalysts(Figure 13b),[368]which is a good start for the development of new non-metal catalysts descriptors.

Figure 13.a)Schematic diagram of orbital hybridization between the C and adsorbate atoms,forming fully filled bonding(σ)and antibonding(σ*)orbitals.Reprinted with permission from Ref.[426]Copyright 2018,The Royal Society of Chemistry.b)The volcano curves of the negative ΔG*O-ΔG*OH versus the calculated O p-band centers relative to Fermi level for Ba3LnIr2O9series.Reprinted with permission from Ref.[368]Copyright 2020,Elsevier B.V.c)The optimized binding geometries of CH3OH,CH2OH,and OCH3on uncharged Pt(111)in vapor and Aqueous phase.Reprinted with permission from Ref.[277]Copyright 2016,National Academy of Sciences.d)Levels of detail necessary to determine whether a reaction pathway is significant.e)Online model exploration methodology.Reprinted with permission from Ref.[427]Copyright 2017,Nature Publishing Group.

In practice,the electrocatalytic processes occur in a complex reaction environment surrounded by electrolyte,whereas the DFT calculations are usually carried out in vacuum,leading to a difference between experimental and computational results.Moreover,the components of electrolyte,including surface coverage,electrode potential,solvent effect,and pH,have a significant effect on catalytic performances.[264,276-278]It is rather challenging to take all these effects into account accurately in DFT calculations.The explicit or implicit solvation models can be adapted to treat solvation effects.For example,the explicit approach is to put several water layers into a supercell to simulate the aqueous electrolyte(Figure 13c),yielding a correction of reaction energy in the subsequent calculations.[277,379,428]However,the number of water molecules which can be added to the supercell is limited by the computing resources.The combined QM/MM method can be partitioned into a region which necessitates a quantum mechanical description(the active site)while the remainder of the system can be treated as a perturbation to the QM region and therefore can be approximated adequately by a molecular mechanics description.[429]This approach speeds up the calculation and can be applied to larger and complex systems including electrolyte.[430-433]

Machine learning is emerging as a promising computational tool for screening efficient catalysts based on experimental results and DFT calculations.Modeling catalyst surface chemistry is a multistep process,from understanding intermediate adsorption configurations to identifying kinetic reaction barriers.Nonetheless,the determination of the rate-limiting steps in the reaction network is computationally expensive.Ulissi et al.[427]built a surrogate model based on group additivity fingerprints using scaling relations and DFT calculations,and Figure 13d presents the key elements in their model.They combined machine learning and group additivity to estimate the free energy of each intermediate species.Then,linear scaling relations are established to predict transition state energies,which reduces the computational cost as compared to the brutalforce DFT calculations.The last step is to analyze the rate-limiting step by tracking transition states.Figure 13e is the work flow of model refinement.In each iteration,the most likely pathway will be selected for calculation with full accuracy(DFT/BEEF-vdW).They successfully applied this model to identify the most likely ethanol production mechanism on rhodium (111).Their study showcased a substantial step forward in combining machine learning and computational DFT catalysis,which is helpful for catalyst screening.Apart from the abovementioned successful applications, the machine learning methods still display many shortcomings at present.For example,the high cost of data curation and model training with high accuracy is an extremely challenging.Meanwhile,the accuracy of machine learning potentials is restricted by the level of DFT.

In addition to machine learning,one promising approach for computational electrocatalystdesign in the presence of complex reaction environments is to develop the concurrent multiscale modeling method[434]which couples DFT,molecular mechanics,coarse-grained models,phase- field methods,and finite element methods in an affordable way.It is a great opportunity for the development of multiscale modeling and calculation methods,which enable to uncover invaluable mechanisms of complex catalytic process with entanglement of spatial and temporal scales.At present,the largely static couplings between the descriptions at the various scales during the treatment of dynamic and adaptive catalysts is the challenge.Integrating emerging machine learning approaches into the multiscale modeling frameworks seems like a promising prospect toward the catalytic systems with higher structural and environmental complexity.[435,436]

In conclusion,DFT-assisted electrocatalysts design has witnessed enormous growth,and DFT calculations play a crucial role in understanding catalytic mechanisms and providing guidelines for the design of new efficient electrocatalysts.Although new challenges are emerging in the field of electrocatalysis,developments of the new DFT-based multiscale models and machining learning methods will bring a bright future for computational electrocatalysis.

Acknowledgments

X.L.and R.L.contributed equally to this work.We thank the following funding agencies for supporting this work:Foshan Xianhu Laboratory of the Advanced Energy Science and Technology Guangdong Laboratory(XHT2020-003);the Fundamental Research Funds for the Central Universities(WUT:2020Ⅲ029,2020IVA100).

Conflict of Interest

The authors declare no conflict of interest.