深埋巷道的爆破开采活动对邻近巷道稳定性影响研究

俞祥杰，陈 晨，张 羽，廖 胜

(合肥工业大学土木与水利工程学院，安徽 合肥 230009)

改革开放以来，我国经济社会高速发展，更多的城市地下空间及地下矿产资源被开发来满足经济发展的需要，大量的地铁、人防地下通道、国防工程坑道和洞库、市政设施地下通道等地下工程已成为我国国民经济、人民生活和国防建设的重要组成部分。地下工程的建造必然会使用爆破施工方法，由于爆破施工自身的破坏性，对建筑物、基础设施及人身安全造成严重威胁，其中爆破产生的冲击荷载将使硐室围岩的裂隙进一步发展，弱化岩石的完整性，甚至引发地下和地表构筑物损毁、巷道冒顶等工程事故。因此，如何避免爆破开挖所产生的冲击荷载对邻近硐室稳定性产生影响，对地下巷道群掘进的安全具有重要意义。

目前，国内外就爆破开采活动对邻近巷道稳定性进行了大量研究，取得了一些成果。徐振洋等[1]分析爆心距与装药量对岩石测震信号的影响，发现爆破的能量频带主要位于10～60 Hz；乔宪队等[2]研究爆破开采作业对周边巷道的影响，分析了周边巷道的振速、应力及其位移的分布情况；阳生权[3]对岩体进行了动力计算，分析了在爆破影响下围岩的位移和应力变化情况；AKIYOSHI等[4]通过求解波动方程，分析了纵波影响下圆形硐室的动应力响应情况；易长平等[5-6]通过研究振动波对周边巷道的作用，分别讨论了波频、巷道尺寸、巷道围岩种类等因素对硐室围岩安全振速的影响问题；刘小乐等[7]基于HHT方法，从三维Hilbert谱、瞬时能量谱及边际谱3个方面对爆破振动信号进行了分析。近些年来，数值计算方法在地下结构抗爆设计中得到广泛应用[8-11]，并为一些复杂问题的解决提供了很好的方案。本文针对某铁矿的既有出矿巷道由于邻近巷道爆破开采而引起面向爆源侧片帮的工程实例，对爆破振动对于邻近既有巷道的影响进行分析研究，以期对爆破危害进行初步探讨，并能够指导工程实践。

1 工程概况

1.1 工程背景

中部地区某铁矿属一类大型铁矿、硫铁矿与硬石膏共生矿床，铁矿石储量丰富，主要采用垂直深孔阶段空场嗣后充填和中深孔分段空场嗣后充填采矿方法进行开采。该矿山岩体中存在大量的断层、节理等地质构造，随着地下开采深度的逐渐增加，地压所带来的危害逐渐凸显，爆破振动对周围巷道的稳定性影响也越来越大。该铁矿开采形成空场后，因岩体既有裂隙的存在以及爆破开采的扰动作用，大面积暴露的矿房侧帮极易产生岩体片帮，对矿柱的稳定性具有较大影响，中间条柱破坏如图1所示。

图1 条柱破坏现场Fig.1 Failure site of strip column

1.2 振动测试试验方案

根据该矿山现场矿柱破坏情况，选择-500 m中段采场进行爆破振动测试，收集现场测试振动数据。考虑到人员安全和仪器保护，共布置5个爆破测振点，本次振动测试采用加拿大Instantel振动监测仪Blastmate Ⅲ对爆破振动效应进行测试，探头采用三轴地震检波器，测试爆破过程中岩体质点的三向速度和岩体三向波速。通过现场试验，分析在爆破开采扰动作用下，邻近既有巷道波速变化及围岩破坏的规律。

2 数值计算模型

本文以某铁矿-500 m中段采场出矿巷道为原型进行数值模拟，分析爆破开采活动对邻近巷道的影响。模型主要是两条埋深500 m的平行直墙式巷道，直墙高度为5 m，拱高为3 m，宽度为6 m，两巷道中心距为12 m，影响范围长为30 m，宽为55 m，高为50 m。考虑到模型的复杂性及计算结果的精确度，对计算模型进行简化的同时，也对巷道及其周边岩体进行了单元加密处理，尽可能提高数值模拟计算的精度。如图2所示，模型共生成了460 896个单元体，模型左边巷道为既有巷道，右边巷道为邻近巷道。既有巷道内沿y轴方向每隔3 m布一组监测点，监测点布置如图3所示。

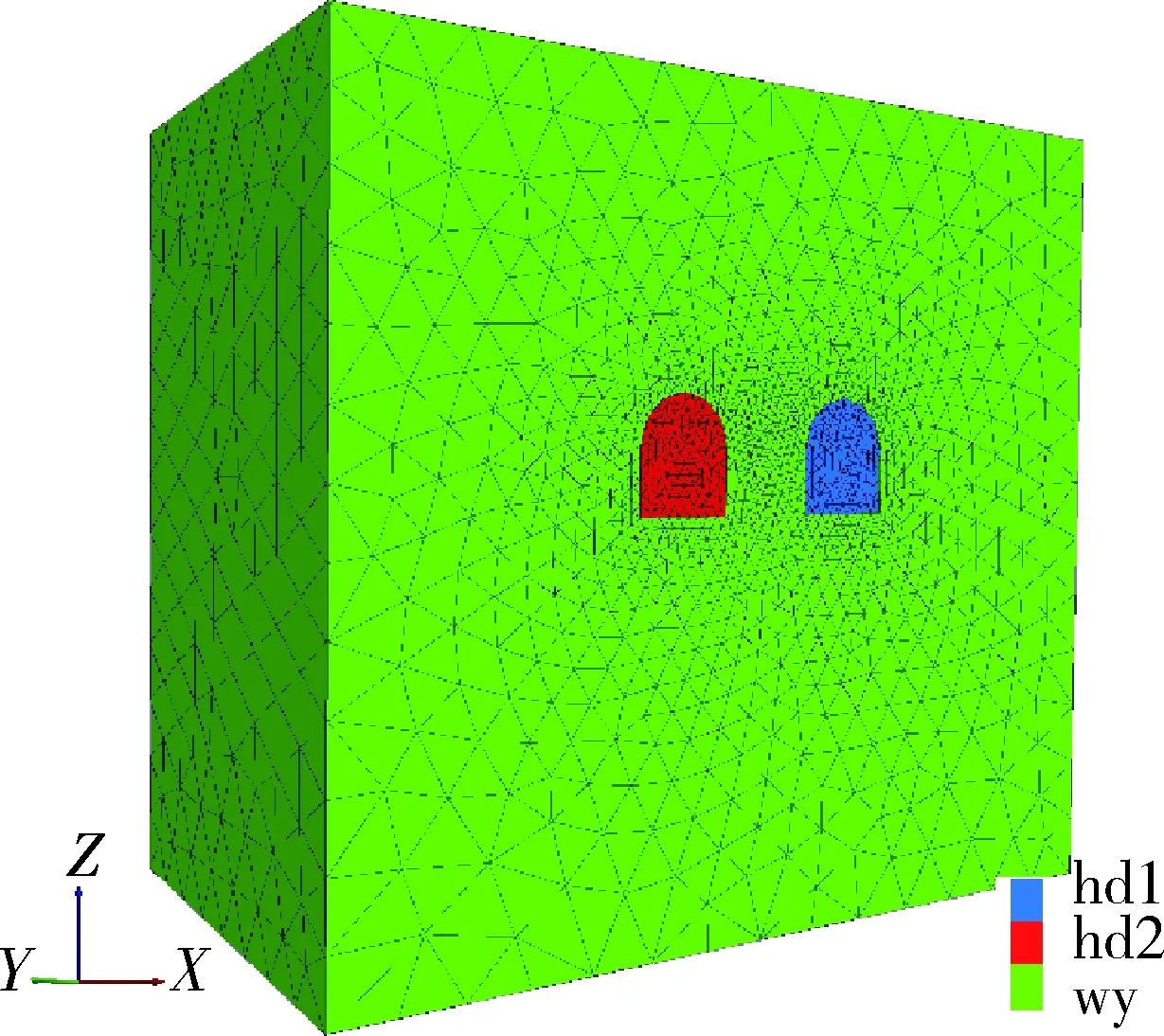
图2 计算模型Fig.2 Calculation model

图3 巷道断面监测点布置Fig.3 Layout of monitoring points for roadway section

本次数值计算分析了σv=13.4 MPa，σh=3.35 MPa的应力条件下，爆破开挖对邻近既有巷道产生的影响(规定邻近巷道沿y轴正轴方向开挖，每次开挖3 m)。开始时对模型四周及底部施加位移约束，顶部保留自由边界；当静力部分计算完成后，为避免模型边界对波的反射影响，去掉施加边界条件，对模型重新施加黏滞边界条件，再进行爆破荷载计算，具体的岩石力学参数见表1。

表1 岩石力学参数Table 1 Rock mechanical parameters

整个数值模拟计算主要由静力计算和爆破荷载计算组成。静力计算是爆破荷载计算的基础，当进行静力计算时，沿着y轴每步开挖3 m，整个过程分10步完成；静力开挖结束之后，将速度时程添加到之前形成的巷道围岩上，进行爆破荷载计算。

3 数值模拟结果分析及现场监测

3.1 位移分析

既有巷道在邻近巷道自重应力和爆破载荷作用下的水平位移分布如图4所示。由图4可知，邻近巷道开挖后，由于重力的存在，既有巷道四周会发生“收缩”，相较于邻近巷道的初始状态，既有巷道左右两侧边墙分别产生了1.51 mm和7.39 mm的朝内收缩位移；当施加动荷载后，周边岩体应力场发生二次重分布并局部发生应力集中现象，围岩位移也随之增大。从总体上看，既有巷道的两侧边墙的水平方向位移都有较大的增长，分别达到了6.3 mm和16.3 mm，特别是面向爆源侧边墙水平位移相较于自重应力作用状态，增幅高达68.2%，这表明邻近巷道的爆破振动使既有巷道在水平方向上产生明显的位移，并且靠近爆源侧围岩变化更明显，这与现场观测结果相符，说明在矿体不断爆破开采过程中，既有巷道围岩特别是靠近爆源侧围岩受到较大的冲击荷载影响，容易处在一种比较危险的状态。

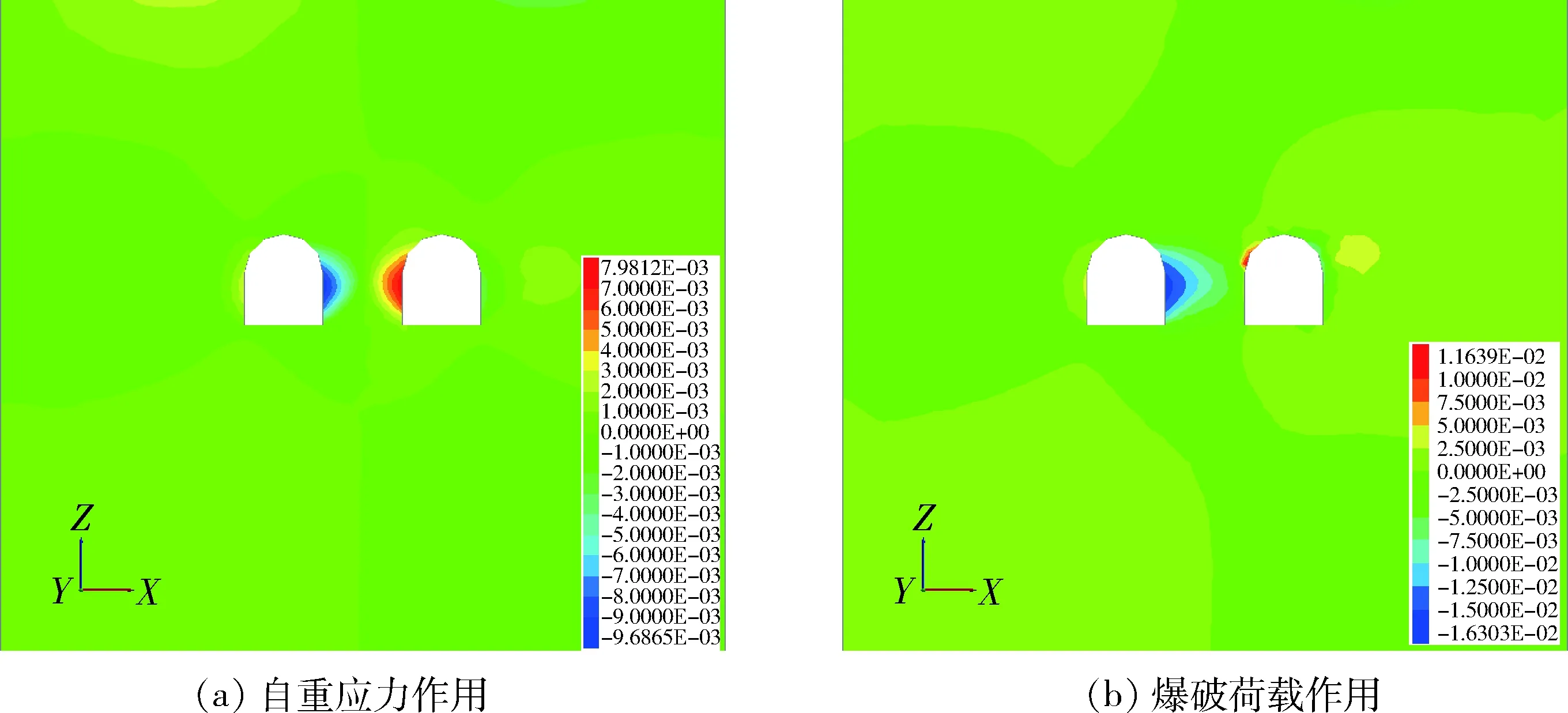
图4 水平位移分布Fig.4 Horizontal displacement distribution

3.2 应力分析

既有巷道在邻近巷道自重及爆破载荷影响下的最小主应力分布如图5所示。从图5(a)中可以看出，在邻近巷道掘进后，在自重应力作用下既有巷道产生了较为显著的拉应力集中现象，拉应力主要集中于既有巷道的顶板以及底板处，最大拉应力达到了0.739 MPa。而通过图5(b)可知，当邻近巷道施加爆破荷载作用后，应力集中区域有着明显的扩大，最大压应力与拉应力都也有着较大程度的增加，最大拉应力甚至达到了1.17 MPa，与自重应力作用状态相比，增幅高达58.6%，且靠近爆源侧围岩变化更明显，这与现场靠近爆源侧围岩容易发生破坏的现象相符。

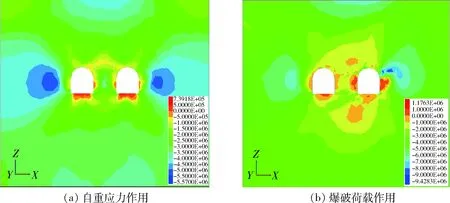
图5 最小主应力分布Fig.5 Minimum principal stress distribution

3.3 塑性区分析

自重应力作用和爆破荷载作用下塑性区分布如图6所示。由图6可知，矿体的开采必然引起周边岩体扰动与破坏，开采过程中岩体受力比较复杂。从塑性区分布情况来看，自重应力作用下既有巷道的塑性区主要分布在巷道周围岩体，各部分破坏形式也各不相同，有拉伸破坏、剪切破坏以及两种破坏形式共存等形式，其中以两种破坏共存的形式为主。而在爆破荷载作用下，由于爆破所产生的冲击荷载的影响，塑性区分布范围比自重应力作用下大得多，并且迎爆侧边墙的岩体由原来的剪切破坏变为了拉伸与剪切破坏这两种破坏共存在的形式，产生了大量塑性积累，具有发生破坏的趋势，这说明爆破振动对既有巷道面向爆源侧边墙处岩体造成的损伤最为严重。结合图4可知，同一位置处塑性区范围变化与其位移变化有着密切关系，塑性区增加的范围越大，位移变化就越大，该位置处岩体的稳定性也越差。

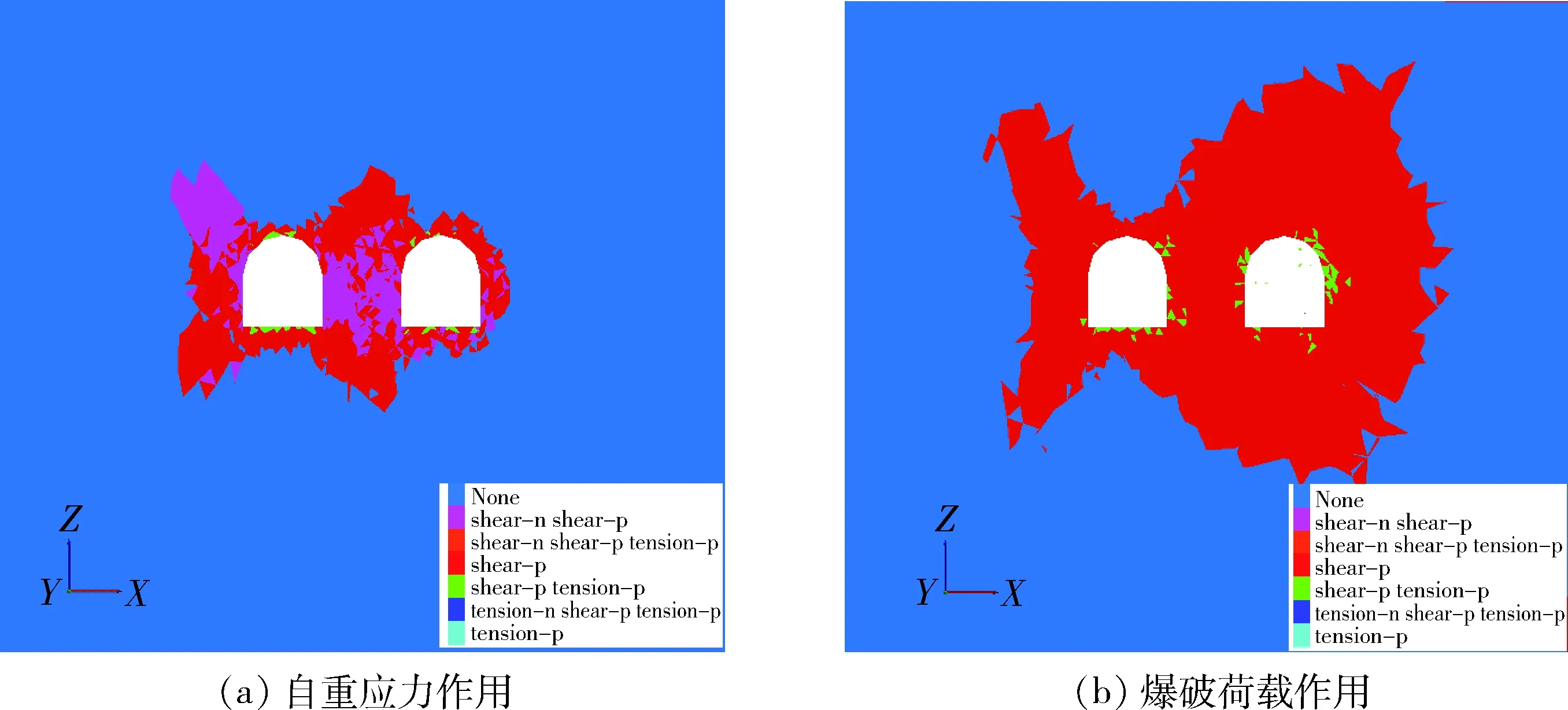
图6 塑性区分布Fig.6 Distribution of plastic zones

塑性区总体积变化如图7所示。从图7可以看出，无论是自重应力作用下还是爆破荷载作用下，塑性区体积随着开挖步数增加基本上呈现线性增长的态势，爆破荷载作用下的塑性区体积增长速度明显快于自重应力作用下，并且同自重应力作用状态相比，爆破荷载作用下的塑性区体积增幅达到了76.5%，这同图6所示的塑性区分布的趋势相符合，这也从一定程度表明爆破荷载所生成的冲击荷载较为明显的影响到了既有巷道的安全性，同现场调查情况相符。

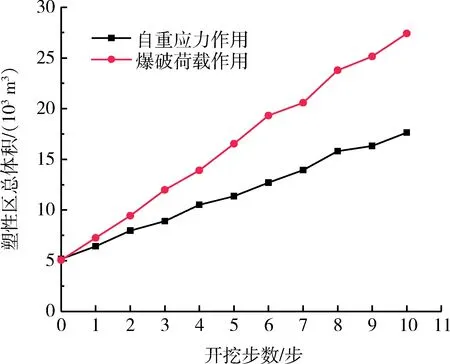
图7 塑性区总体积变化Fig.7 Total volume change of plastic zone

3.4 振速分析

由于实际中常常用巷道围岩的峰值振动速度来判断洞室稳定性好坏，因此计算中重点对巷道围岩的振动速度进行了监测，监测的截面包括了y=3 m、y=9 m、y=15 m、y=21 m、y=27 m这五处剖面，各剖面监测点的峰值振速分布如图8所示。由图8可知，这五个剖面中，靠近爆源侧直墙中部振速最大，这是由于此区域同爆心位置高度较为一致，位于振动波垂直入射的区域，受到爆破的影响最大，发生破坏的可能性也最大；靠近爆源侧直墙下部振速也比较大，这是因为此区域振动波入射角也比较小，但由于底角的夹制作用，直墙下部的危险度要明显比直墙上部小一些，是既有巷道中的次危险部位；由于拱圈的作用，靠近爆源侧拱脚以上部位的振动波入射角度是逐渐变大的，振动波能量的输入得以减小，拱脚到拱顶区域的振速也渐渐减小；而远离爆源侧直墙围岩的振速偏小，这是因为远离爆源侧的振动波的传播是需要绕射的，振动波的强度会得到极大的减弱。综上所述，邻近巷道爆破振动对既有巷道靠近爆源侧边墙中上部围岩的稳定性影响最明显，进行爆破作业时要加强对该区域的支护。

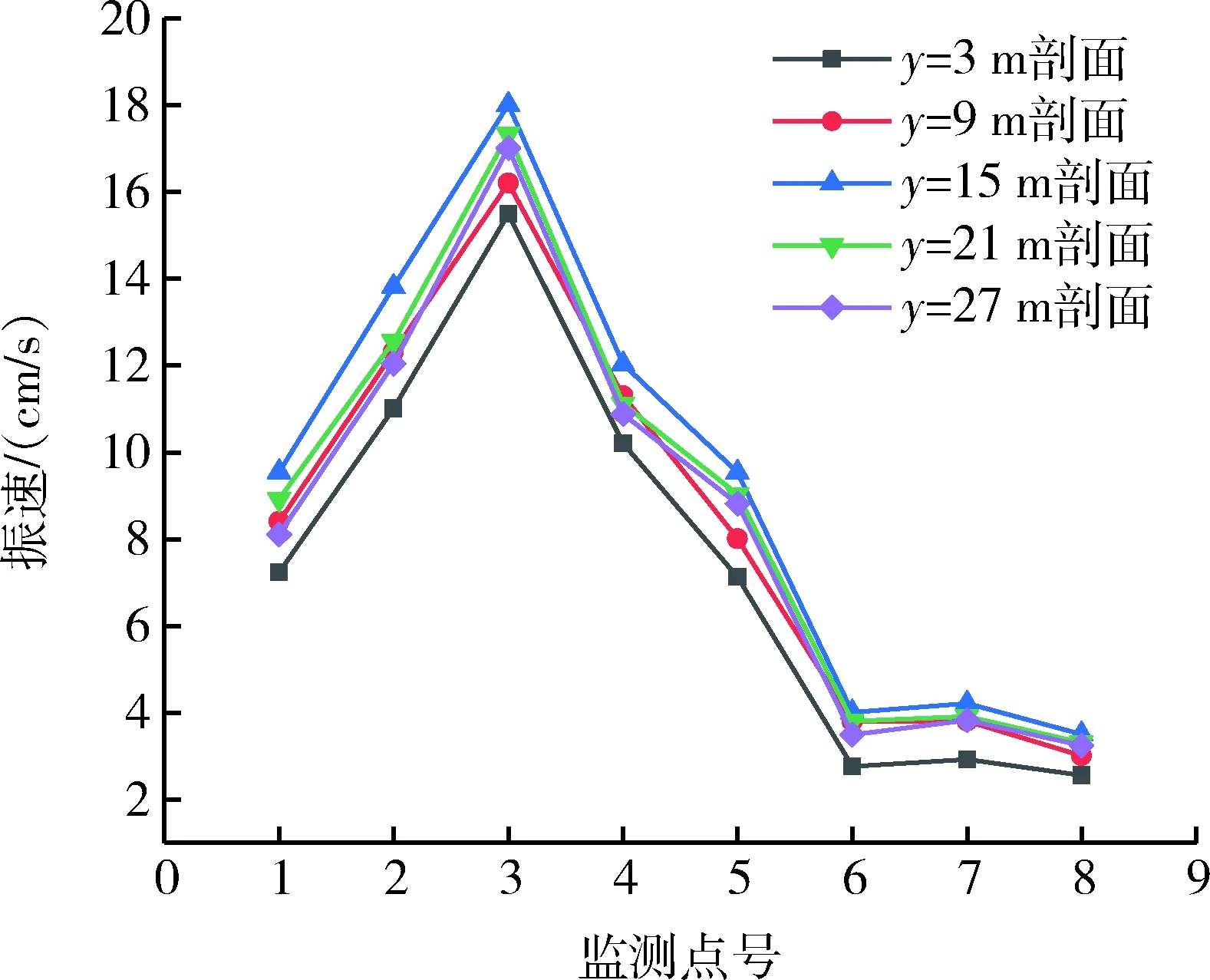
图8 各剖面监测点X向峰值振速分布Fig.8 X-direction peak vibration velocity distribution of each profile monitoring point

3.5 数值模拟结果与实测数据对比分析

通过数值模拟计算，可以获得在爆破冲击荷载下每个监测点的三向振动曲线。将数值模拟结果与现场测量数据展开对比分析，研究爆破规律，验证本次数值模拟计算的准确性。限于篇幅，仅选取X方向振动曲线同现场实测数据进行对比分析，数值模拟X向振动曲线与现场切向振动曲线如图9所示，数值模拟计算曲线与现场实测曲线的的波峰数量、峰值振速都比较一致，并且波形的持续时间也近乎相同，但是数值计算曲线同现场实测曲线的波峰出现的时间有一定误差，这是因为现场实测的振动曲线的切向、径向和垂向同数值模拟中的坐标系之间一定存在着无法避免的偏差，且爆破影响因素较多，造成上述两条曲线之间存在着误差。从总体上来说，数值计算所得振动曲线同实测振动曲线的分布趋势较为一致，这说明了本次数值模拟计算所建立的模型是可靠的，上述计算结果的精度和准确性都是有所保证的。

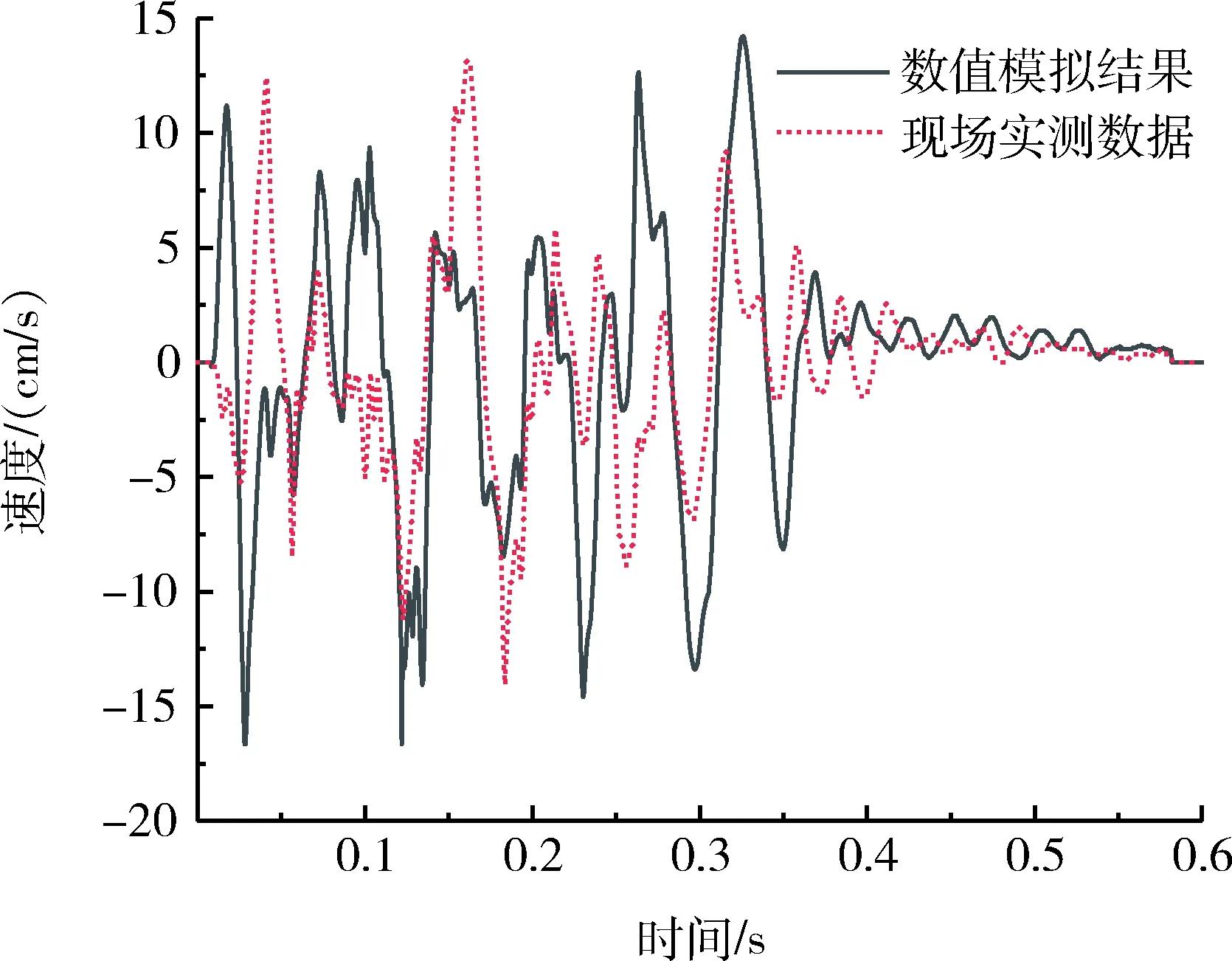
图9 数值模拟X向振动曲线与现场切向振动曲线Fig.9 Numerical simulation X-direction vibration curve and field tangential vibration curve

4 结 论

1)同自重应力状态相比，爆破载荷影响下既有巷道围岩的最大水平位移、最大拉应力及塑性区体积有着很大程度的增长，增幅分别达到了68.2%、58.6%及76.5%，既有巷道发生失稳破坏的概率显著增加。

2)既有巷道截面稳定性由差到好的区域依次为靠近爆源侧围岩中部到拱圈区域、靠近爆源侧拱圈以上区域和靠近爆源侧底角及远离爆源侧，靠近爆源侧围岩的拉应力主要是爆破所产生冲击波的反射作用造成的，而远离爆源侧围岩由于主要受到冲击波的绕射作用，故受影响较小。

3)为避免爆破引发邻近既有巷道失稳破坏，需加强对既有巷道的迎爆测直墙中上部等危险部位的监测与支护，并对地质条件薄弱区域及时采取素喷混凝土、锚网喷混凝土等有效的支护措施。