ε-(AlxGa1-x)2O3/ε-Ga2O3异质结电子输运性质研究
白雅楠,吕燕伍
(北京交通大学理学院,北京 100044)
0 引 言
Ga2O3是一种很有吸引力的宽带隙半导体材料,由于其高击穿场强和超宽带隙[1]的特点,正在成为一种很有前景的高功率开关电子器件、光电探测器和日盲紫外探测器的材料。Ga2O3有五种晶型[2],其中β-Ga2O3是最稳定也是研究最多的相,调制掺杂诱导的高密度二维电子气(2DEG)会导致β-(AlxGa1-x)2O3/Ga2O3异质界面2DEG沟道迁移率的增加,这是由于减少了电离杂质散射并且增强了2DEG沟道对声子模式的屏蔽。要想获得高密度的2DEG,需要对β-(AlxGa1-x)2O3阻挡层进行大量的掺杂以及插入极薄的隔离层,同时还需要严格控制生长参数和突变的异质界面以及尖锐的掺杂轮廓[3]。β-Ga2O3晶体结构具有对称中心,但缺乏任何特殊性质,如压电性、铁电性等[4];而Ga2O3的亚稳相ε-Ga2O3,由于其超宽的带隙和独特的材料特性引起了人们的兴趣。
早在1952年,Roy等[5]通过对Ga(NO3)3进行热分解合成了ε-Ga2O3,他们发现ε-Ga2O3在870 ℃时保持稳定,但是对它的晶体结构一直不清楚。直到2013年Playford等[6]报道了ε-Ga2O3的晶体结构,确定了ε-Ga2O3属于正交晶系,空间群为Pna21(a=0.513 nm,b=0.88 nm,c=0.942 nm)。在2015年,Oshima等[7]证明了使用氢化物气相外延(HVPE)法可以在GaN、AlN和β-Ga2O3衬底上生长纯相ε-Ga2O3薄膜,确定了ε-Ga2O3薄膜的带隙为4.4 eV,表明ε-Ga2O3在制造高性能太阳盲探测器方面具有很大的应用潜力。此外,Maccioni等报道ε-Ga2O3/GaN晶体管在异质结界面上可能具有较高的2DEG浓度(1014cm-2),并且它可能大大优于AlGaN/GaN的2DEG浓度(1013cm-2)[8]。这是因为与Ш族氮化物半导体相比,ε-Ga2O3也具有自发极化和压电极化,并且ε-Ga2O3的自发极化比Ш族氮化物半导体(如GaN和AlN)高近一个数量级,可以在没有掺杂的情况下在异质界面形成高浓度的2DEG,类似于AlxGa1-xN/GaN异质界面,ε-(AlxGa1-x)2O3/ε-Ga2O3具有相对较低的晶格失配,通过优化生长条件,可以在ε-(AlxGa1-x)2O3/ε-Ga2O3异质界面形成高达1014cm-2的2DEG[9]。
与其他的Ga2O3基异质结相比,ε-(AlxGa1-x)2O3/ε-Ga2O3异质结具有相对比较强的自发极化和压电极化,所以异质结界面存在高密度和高迁移率的2DEG,因此可以广泛应用于高频、大功率半导体器件领域,为了进一步提高ε-(AlxGa1-x)2O3/ε-Ga2O3高电子迁移率晶体管(HEMT)的器件性能。本文以ε-(AlxGa1-x)2O3/ε-Ga2O3异质结结构中的ε-(AlxGa1-x)2O3势垒层为研究对象,考虑有限厚度的势垒层和异质结界面的自发极化和压电极化效应,给出ε-(AlxGa1-x)2O3/ε-Ga2O3异质结结构的2DEG特性,在不同Al摩尔组分和ε-(AlxGa1-x)2O3势垒层厚度的情况下,研究它们对2DEG浓度、合金无序散射、界面粗糙度散射和极性光学声子散射的影响,研究结果对控制ε-(AlxGa1-x)2O3/ε-Ga2O3异质结构中的2DEG浓度和提高电子迁移率具有一定意义。
1 理论模型与计算方法
1.1 ε-(AlxGa1-x)2O3/ε-Ga2O3HEMT结构中的2DEG浓度
实验上使用金属有机化学气相沉积法(MOCVD)在c面蓝宝石衬底上生长ε-(AlxGa1-x)2O3/ε-Ga2O3异质结,采用水(H2O)和三甲基镓(TMG)作为试剂和钯纯化的H2作为载体,TMG的温度和压力保持在650 ℃和104Pa,实验结果表明使用H2O要比使用纯氧的效果更好,这是由于原子氧相对于分子氧从水中解离出来的反应性更高,H2O和TMG的分压比在100~1 000范围内变化,通常设定为200[10]。晶体的生长方向为c对称轴,把这个方向记为z轴,x-y平面是垂直于z轴的平面,图1是ε-(AlxGa1-x)2O3/ε-Ga2O3HEMT的基本结构示意图,它的结构是在较厚的ε-Ga2O3层上覆盖一层厚度为几纳米到十几纳米的ε-(AlxGa1-x)2O3,上面是一个由肖特基结充当的栅极,Au和Ti常作为栅极材料[11]。因为ε-(AlxGa1-x)2O3的禁带宽度较大,所以电子会积累在ε-(AlxGa1-x)2O3/ε-Ga2O3异质结下表面的势阱中从而形成2DEG,并且由于ε-(AlxGa1-x)2O3/ε-Ga2O3异质结本身具有很强的自发极化和压电极化效应[12-14],异质结的2DEG浓度可达到1014cm-2[9],ε-(AlxGa1-x)2O3/ε-Ga2O3异质结的能带图如图2所示。
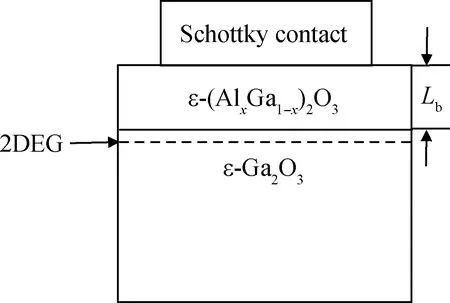
图1 ε-(AlxGa1-x)2O3/ε-Ga2O3 HEMT基本结构图Fig.1 Structure of ε-(AlxGa1-x)2O3/ε-Ga2O3 HEMT

图2 ε-(AlxGa1-x)2O3/ε-Ga2O3异质结能带图Fig.2 Band diagram of ε-(AlxGa1-x)2O3/ε-Ga2O3heterojunction
由于ε-(AlxGa1-x)2O3和ε-Ga2O3晶格的非对称性,导致单位晶胞内的正负电荷中心不重合,形成偶极矩,所以ε-Ga2O3具有很强的自发极化效应,极化方向如图3所示[15]。对于ε-(AlxGa1-x)2O3层,通过对κ-Al2O3和ε-Ga2O3的物理量进行线性差值得出ε-(AlxGa1-x)2O3的相关物理量,其中x表示Al的摩尔分数,表1列出计算中所用参数,ε-(AlxGa1-x)2O3自发极化强度PSP(x)为:
PSP(x)=(-0.033x-0.242) C/m2
(1)
由于ε-(AlxGa1-x)2O3与ε-Ga2O3晶格不匹配,所以两晶格内部存在应变。在ε-(AlxGa1-x)2O3层,应变在垂直于生长的方向是伸张的;在ε-Ga2O3层,应变在x-y方向是压缩的。相比于几百纳米以上的ε-Ga2O3层,几纳米到十几纳米的ε-(AlxGa1-x)2O3作为薄层处理,因此可以近似地认为应变存在于ε-(AlxGa1-x)2O3层中,并产生压电极化效应[15-16]。

图3 ε-(AlxGa1-x)2O3/ε-Ga2O3自发极化和压电极化方向Fig.3 ε-(AlxGa1-x)2O3/ε-Ga2O3 spontaneous polarization and piezoelectric polarization directions

表1 κ-Al2O3和ε-Ga2O3的各项物理参数(300 K)[9,20-21]Table 1 Physical parameters of κ-Al2O3 and ε-Ga2O3(300 K)[9,20-21]
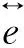
(2)
PPE=e31εxx+e32εyy+e33εzz
(3)
近似计算了ε-Ga2O3沿z方向生长的外延层中的应变分量:
(4)
(5)
(6)
式中:a0、b0表示平衡时衬底ε-Ga2O3的晶格常数;a和b表示外延层ε-(AlxGa1-x)2O3的晶格常数。将式(4)、(5)、(6)代入(3)中可得压电极化表达式为[19]:
(7)
(8)
ε-(AlxGa1-x)2O3是κ-Al2O3和ε-Ga2O3的合金,假设Al的组分为x,根据Vegard定律,可以得到相应的ε-(AlxGa1-x)2O3材料中的极化相关参数如下:
a(x)=(-0.025x+0.513) nm
(9)
b(x)=(-0.041x+0.880) nm
(10)
e31(x)=(-0.049x+0.095) C/m2
(11)
e32(x)=(-0.044x+0.079) C/m2
(12)
e33(x)=(0.107x-0.163) C/m2
(13)
C13(x)=(24x+125) GPa
(14)
C23(x)=(-9x+125) GPa
(15)
C33(x)=(169x+207) GPa
(16)
将以上公式代入式(8)得出ε-(AlxGa1-x)2O3的压电极化表达式。
在自发极化和压电极化的共同作用下,在ε-(AlxGa1-x)2O3/ε-Ga2O3异质结界面出现了极化面电荷,相同方向的压电极化和自发极化使得ε-(AlxGa1-x)2O3/ε-Ga2O3异质结界面的极化电荷密度较大,极化面电荷密度的表达式如下[22]:
σε-(AlxGa1-x)2O3/ε-Ga2O3=|PSP[ε-(AlxGa1-x)2O3]+PPE[ε-(AlxGa1-x)2O3]-PSP[ε-Ga2O3]|
(17)
根据电中性原理和高斯定理可得ε-(AlxGa1-x)2O3/ε-Ga2O3异质结的2DEG浓度ns的表达式为[23]:
(18)
式中:e是电子电量;Lb是ε-(AlxGa1-x)2O3层的厚度;εε-(AlxGa1-x)2O3是ε-(AlxGa1-x)2O3的介电常数;EF是界面处费米能级和ε-Ga2O3导带底之间的差值,EF可以表达如下[24-25]:
(19)
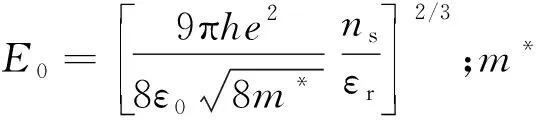
eφB=(0.92x+0.9) eV
(20)
ΔEc(x)是ε-(AlxGa1-x)2O3和ε-Ga2O3之间的导带差值,假设ε-(AlxGa1-x)2O3和ε-Ga2O3界面为理想界面,利用线性插值法得出界面的导带阶表达式为[27]:
ΔEc=0.6[xEg(κ-Al2O3)+(1-x)Eg(ε-Ga2O3)-Eg(ε-Ga2O3)]+1.5x(1-x)
(21)
1.2 ε-(AlxGa1-x)2O3/ε-Ga2O3 HEMT结构中的合金无序散射
合金无序散射源于势垒中随机变化的合金无序电势,且这种散射形式是在合金通道中2DEG载流子迁移率的限制机制,在被限制在势阱的2DEG中,由于2DEG波函数有限地渗透到势垒中而发生合金无序散射[28]。ε-(AlxGa1-x)2O3/ε-Ga2O3材料中合金无序散射的弛豫时间可由式(22)描述[29]:
(22)

异质结ε-(AlxGa1-x)2O3/ε-Ga2O3的合金无序散射迁移率由式(23)表述:
(23)
1.3 ε-(AlxGa1-x)2O3/ε-Ga2O3 HEMT结构中的界面粗糙度散射
对于半导体异质结,由于生长过程中的晶格失配、反应源不能及时切换等原因,其界面通常是凹凸不平的,称之为界面粗糙度。异质结界面几何上的不平整相当于一个起伏的势场,使界面2DEG发生散射,界面粗糙度可用两个参数来表征,一个是界面上起伏的高度差Δ,另一个是沿界面方向起伏的平均周期L。用这两个参数可以写出等效的散射势场,从而算出由界面粗糙度散射决定的弛豫时间[30]。其表达式如下:
(24)
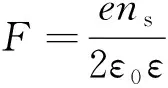
异质结ε-(AlxGa1-x)2O3/ε-Ga2O3的界面粗糙散射迁移率由下式表述:
(25)
1.4 ε-(AlxGa1-x)2O3/ε-Ga2O3 HEMT结构中的极性光学声子散射
极性光学声子散射是高温情况下主要的散射机制,研究人员已经进行了大量的研究[32-34],同时Gelmont、Shur和Stroscio推导出了2DEG中动量弛豫速率的解析表达式[35]。ε-(AlxGa1-x)2O3/ε-Ga2O3的极性光学散射率τOP由下式表示[35]:
(26)
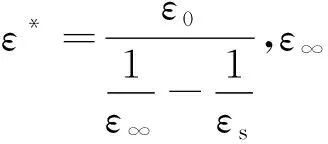
异质结ε-(AlxGa1-x)2O3/ε-Ga2O3的极性光学声子散射迁移率由下式表述:
(27)
2 结果与讨论
本文主要对ε-(AlxGa1-x)2O3/ε-Ga2O3异质结的输运性质进行了研究,接下来将从以下这四个方面来进行讨论:当Al摩尔分数分别为0.2、0.3和0.4时,2DEG浓度与ε-(AlxGa1-x)2O3势垒层厚度的关系曲线如图4所示。由公式(18)可知,2DEG浓度与ε-(AlxGa1-x)2O3势垒层厚度、Al组分含量均存在一定的关系。由图4可以看出,ε-(AlxGa1-x)2O3势垒层会使沟道层中2DEG浓度升高, 但Al摩尔组分的增加会在一定程度上提高2DEG的浓度。Al摩尔组分含量越高, 2DEG浓度随ε-(AlxGa1-x)2O3势垒层厚度的升高越快,且当ε-(AlxGa1-x)2O3势垒层的厚度处于区间5~6 nm时,2DEG浓度保持在相对较高的水平。
合金无序散射迁移率和ε-(AlxGa1-x)2O3势垒层厚度的关系曲线如图5所示,由公式(22)可以看出,合金无序散射迁移率与Al组分含量和势阱中2DEG的波函数有关。当ε-(AlxGa1-x)2O3势垒层中Al组分分别为0.2、0.3和0.4时,随着ε-(AlxGa1-x)2O3势垒层厚度的增加,合金无序散射迁移率呈现升高的趋势,不同的Al摩尔组分下的迁移率相差较大。由此可见,Al组分对合金无序散射迁移率的影响较大,ε-(AlxGa1-x)2O3势垒层厚度对合金无序散射迁移率影响较小。

图4 2DEG浓度和ε-(AlxGa1-x)2O3势垒层厚度的关系Fig.4 Relationship between the 2DEG sheet density andbarrier thickness of ε-(AlxGa1-x)2O3
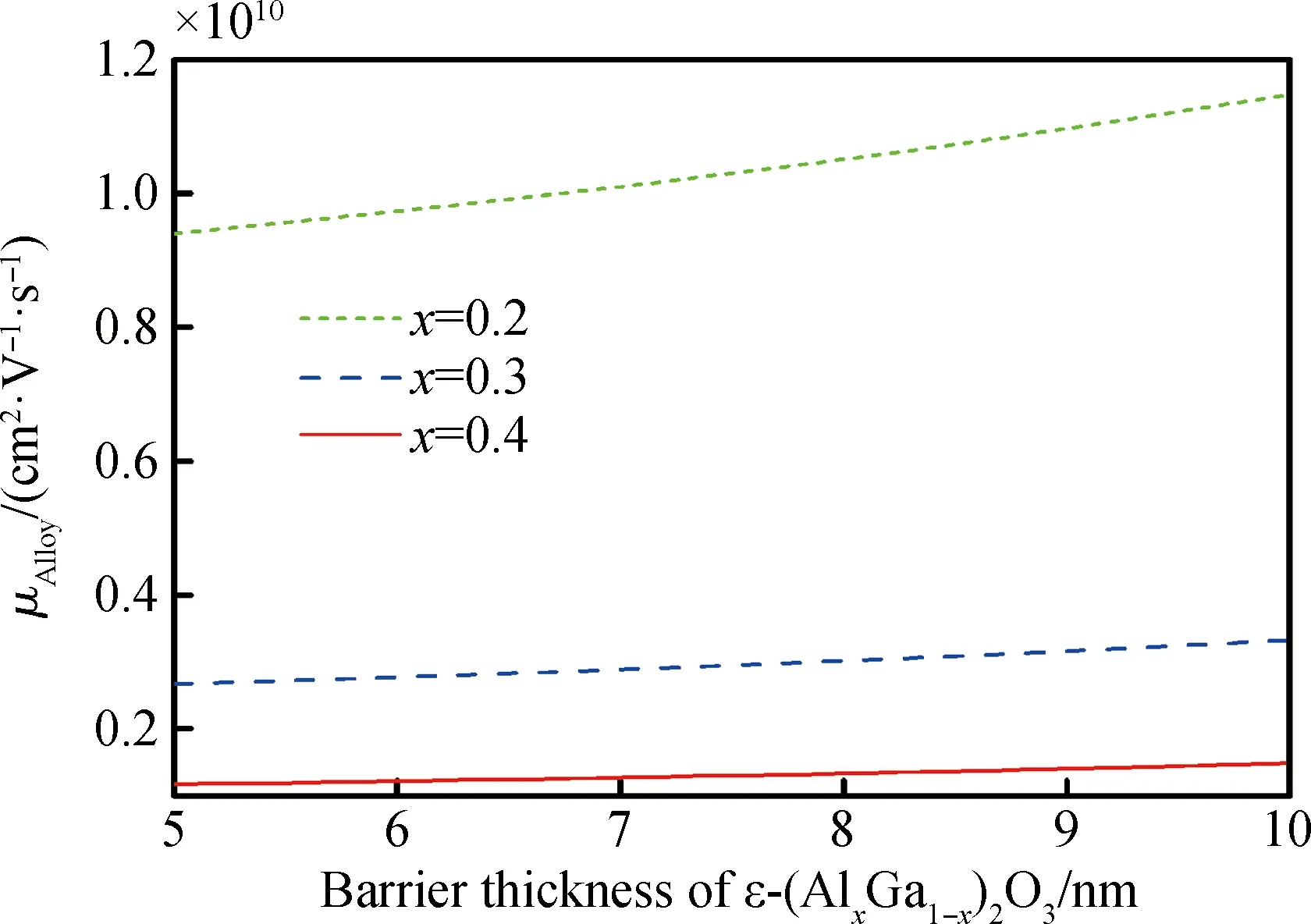
图5 合金无序散射所限制的迁移率与势垒层厚度的关系Fig.5 Relationship between mobility limited by alloy disorder scattering and barrier thickness
界面粗糙度散射迁移率和ε-(AlxGa1-x)2O3势垒层厚度之间的关系曲线如图6所示,由图可知ε-(AlxGa1-x)2O3势垒层的增加会增强界面粗糙度散射,降低界面粗糙度散射的迁移率,且Al摩尔组分越低,随着ε-(AlxGa1-x)2O3势垒层厚度的增加,界面粗糙度散射的迁移率降低越明显,由式(24)和(25)可以看出,界面粗糙度散射迁移率反比于2DEG浓度的平方。由图4可知,ε-(AlxGa1-x)2O3势垒层厚度的增加会使2DEG浓度升高,故随着ε-(AlxGa1-x)2O3势垒层厚度的增加,界面粗糙度散射限制的迁移率降低。换言之,2DEG浓度和界面粗糙度散射的迁移率成反比。
极性光学声子散射迁移率和ε-(AlxGa1-x)2O3势垒层厚度之间的关系曲线如图7所示。保持温度300 K不变,利用表达式(26)和(27)可以得出不同Al组分含量下,极性光学声子散射迁移率和ε-(AlxGa1-x)2O3势垒层厚度的关系。由图可以看出,极性光学声子散射迁移率随ε-(AlxGa1-x)2O3势垒层厚度的增大而降低,且Al摩尔组分越低,极性光学声子散射迁移率随ε-(AlxGa1-x)2O3势垒层厚度的增大降低得越快。
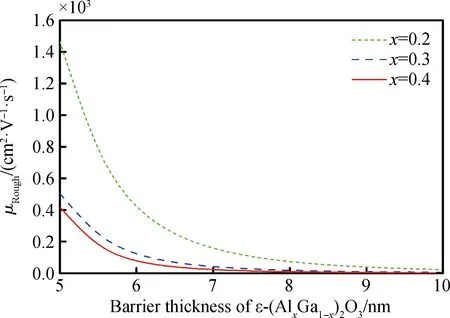
图6 界面粗糙度散射所限制的迁移率与势垒层厚度的关系Fig.6 Relationship between mobility limited by interface roughness scattering and barrier thickness
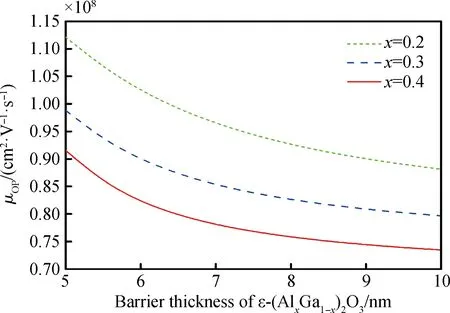
图7 极性光学声子散射所限制的迁移率与势垒层厚度的关系Fig.7 Relationship between mobility limited by polar optical phonon scattering and barrier thickness
综上所述,除了研究合金无序、界面粗糙度和极性光学声子这三种散射对迁移率的影响,还考虑了不同Al摩尔组分下这三种散射所产生的总迁移率与ε-(AlxGa1-x)2O3势垒层厚度之间的关系曲线。如图8所示,发现限制迁移率的主要散射机制是界面粗糙度散射,由图4可知,2DEG浓度随ε-(AlxGa1-x)2O3势垒层厚度的增加在不断升高,因为界面粗糙度散射迁移率反比与2DEG浓度的平方,这时界面粗糙度散射已经成为主导散射机制,所以迁移率会不断减小。总迁移率随ε-(AlxGa1-x)2O3势垒层厚度的增加而降低,并且Al摩尔组分越低,总迁移率随ε-(AlxGa1-x)2O3势垒层厚度的增加而下降得越快。因此,对于ε-(AlxGa1-x)2O3/ε-Ga2O3异质结而言,界面粗糙度散射对载流子的影响最大,极性光学声子散射次之,合金无序散射最弱。

图8 不同Al摩尔组分下,ε-(AlxGa1-x)2O3势垒层厚度和总迁移率的关系Fig.8 Relationship between the thickness of ε-(AlxGa1-x)2O3 and total mobility under different Al mole fraction
3 结 论
本文主要研究了ε-(AlxGa1-x)2O3/ε-Ga2O3异质结的电子输运性质,并且推导出了2DEG浓度的表达式,通过改变不同的ε-(AlxGa1-x)2O3势垒层厚度和Al摩尔组分来研究它们对2DEG浓度、合金无序散射、界面粗糙度散射、极性光学声子散射迁移率和总迁移率的影响。研究发现:(1)ε-(AlxGa1-x)2O3势垒层厚度越大,2DEG浓度越高,从而导致界面粗糙度散射增强,迁移率减小,且Al摩尔组分含量越高,界面粗糙度散射迁移率越低;(2)ε-(AlxGa1-x)2O3势垒层厚度对合金无序散射迁移率的影响较小,且随着ε-(AlxGa1-x)2O3势垒层厚度的增加合金无序散射减弱,迁移率增大;(3)ε-(AlxGa1-x)2O3势垒层厚度的增加会导致极性光学声子散射增强,迁移率减弱,Al摩尔组分含量越高,极性光学声子散射的迁移率越低;(4)总迁移率会随ε-(AlxGa1-x)2O3势垒层厚度的增加而减小,Al摩尔组分越低,总迁移率越高。

