基于矩阵范型的配电网三相谐波潮流算法

林金榕，张 逸，李传栋，邵振国，李宽宏

（1. 福州大学 电气工程与自动化学院，福建 福州 350108；2. 国网福建省电力有限公司电力科学研究院，福建 福州 350007；3. 国网福建省电力有限公司福州供电公司，福建 福州 350009）

0 引言

2020 年我国提出2030 年碳达峰和2060 年碳中和的“双碳”目标。在该背景下，清洁能源的消纳以及分布式电源（DG）的高比例接入，都对配电网的规划和运行提出了更高的要求，由此导致的配电网谐波、三相不平衡等电能质量问题的影响越来越大，这些电能质量问题对配电网的安全运行造成了很大的危害［1-4］。为了评估电能质量问题的影响并为电能质量治理提供依据，三相谐波潮流计算将是一种重要的分析手段。

现有的配电网潮流仿真分析工具［5-6］在处理环网、高渗透率DG 接入引起的多重电能质量问题时建模繁琐、效率较低，而且难以满足在线实时应用需求。文献［7-9］基于前推回代法对三相谐波潮流进行研究，但由于前推回代法固有的局限，在处理各类DG 和局部存在的环网时需要对该方法进行改进［10-12］，这不可避免地增加了算法复杂度，使计算次数增多，收敛性下降。文献［13］基于PQ分解法对三相谐波潮流进行研究，该方法简化了牛顿-拉夫逊法的实现过程，但PQ分解法的应用前提是电抗远大于电阻，而且PQ分解法在算法收敛过程中不修正搜索方向，收敛性差，这导致其在配电网中难以应用。综合现有的研究情况可知，配电网三相谐波潮流的研究方法主要有2 种：一是基于前推回代法的潮流算法，其实现简单，但由于算法固有的梯度简化问题，在配电网DG 高比例接入和电压控制策略日益复杂的情况下，其优势日益削弱，缺陷日益凸现；二是基于牛顿-拉夫逊法的潮流算法，其优势在于搜索方向用的是完整的梯度，收敛性好，同时算法可直接扩展到各类潮流控制策略，其缺点是三相谐波导纳矩阵和雅可比矩阵构造十分复杂，难以构建规范的实现形式，模型扩展和应用难，因此相关研究成果极少。

为了适应未来配电网发展中DG 高比例接入和潮流控制方式日益复杂的情况，本文提出一种通用的规范型式下的三相谐波潮流算法。首先，采用矩阵索引技术生成牛顿-拉夫逊法相关的矩阵；其次，利用矩阵范型生成三相谐波导纳矩阵；然后，利用生成的矩阵计算三相谐波潮流；最后，分别利用IEEE 14 和IEEE 123 节点系统对本文算法的准确性、有效性、效率以及处理环网的能力进行验证分析。

1 三相谐波潮流基础模型

参考文献［14-15］中电气元件对应的谐波等值阻抗，限于篇幅，本文只介绍后文仿真中所使用的模型。

1）线路模型。

当计算的谐波次数不高并且线路长度不大于300 km时，线路单相谐波阻抗近似为：

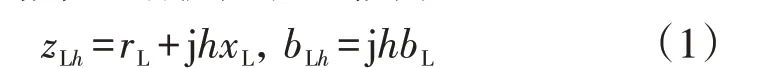
式中：h为谐波次数；r、x、z、b分别为电阻、电抗、阻抗、电纳，下标L表示线路，下标h表示第h次谐波。

2）变压器模型。

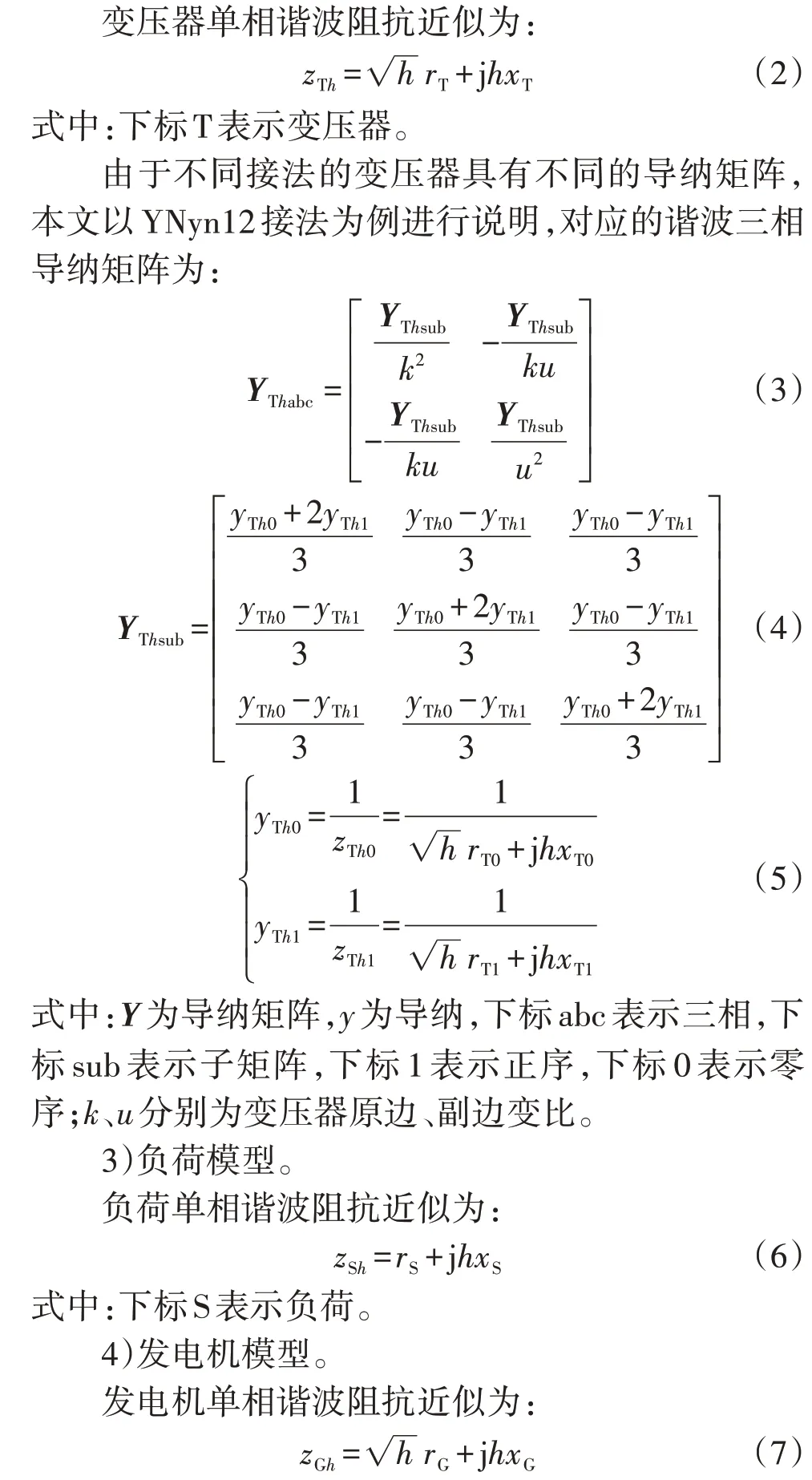
式中：下标G表示发电机。

2 矩阵范型

2.1 矩阵范型算法原理

由于三相谐波潮流模型复杂，相关的工程应用一直难以推进。本文基于矩阵范型框架，提出一种将三相谐波潮流计算中的矩阵元素生成、修改和索引等过程转化为矩阵运算的算法实现框架。该框架组合矩阵内积、关联矩阵和矩阵索引等技术，并通过标准的矩阵运算过程实现电网潮流算法和计算机底层数据结构的解耦。本质上，矩阵范型是一种散列映射算法，其实现了从单相电网的设备序参数列表到三相电网导纳矩阵元素的规范映射。矩阵范型示意图如图1所示。图中：a1—a3为向量的元素；l为矩阵非零元素行坐标；q为矩阵非零元素列坐标；g为矩阵非零元素数值；f为元件首端节点；t为元件末端节点；下标f f表示首端节点对首端节点；下标tt表示末端节点对末端节点；下标f t表示首端节点对末端节点；下标t f表示末端节点对首端节点；⊗表示克罗内克积。此外，由于工程化的需要，本文三相谐波潮流算法中考虑三序参数和三相参数的相互转换、线路和变压器参数到三相谐波导纳矩阵的转换以及矩阵的重排和随机访问。若采用传统的面向元素级别的稀疏矩阵方法来实现以上过程，则编译和调试难度大，且难以实现模型的便捷扩展和算法的功能增加。

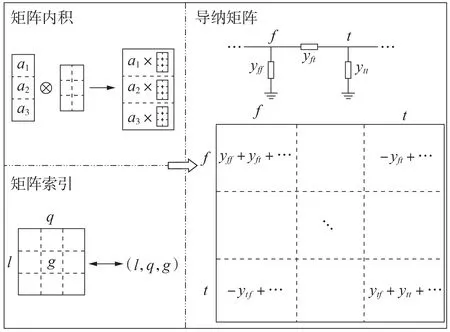
图1 矩阵范型示意图Fig.1 Schematic diagram of matrix paradigm

2.2 矩阵范型过程的实现

为降低配电网三相建模的复杂性，减少计算量，本文将序网参数矩阵作为输入，并通过相应的矩阵范型变换得到本文所需的三相谐波导纳矩阵。范型变换主要分为如下3步。

1）为了便于数据的输入，通过转换矩阵Tr整合同一元件同次谐波的三序参数，并进行相序转换操作，得到三相谐波基础导纳矩阵YHbase，其表示元件首端到末端节点之间的三相支路导纳矩阵，本文称为三相谐波基础导纳矩阵。具体过程如下：

式中：下标H 表示矩阵包含各次谐波分量；下标base表示基础分量参数；下标120 表示三序；Ip为p维单位矩阵，Ep为元素全为1的p维列向量，p=n(m-1)，n为元件总数，m为谐波的最大次数；1∶1∶3p表示以1 为起点，1 为步长，3p为终点的列向量，其他同理；Tabc120、T120abc为相序转换矩阵；函数gsparse(L，M，N)表示以向量L的元素为行坐标、向量M的元素为列坐标、向量N的元素为数值，生成稀疏矩阵。

2）在三相谐波基础导纳矩阵的基础上继续推导出三相谐波子导纳矩阵，包括元件首、末端节点的自导纳矩阵和互导纳矩阵。

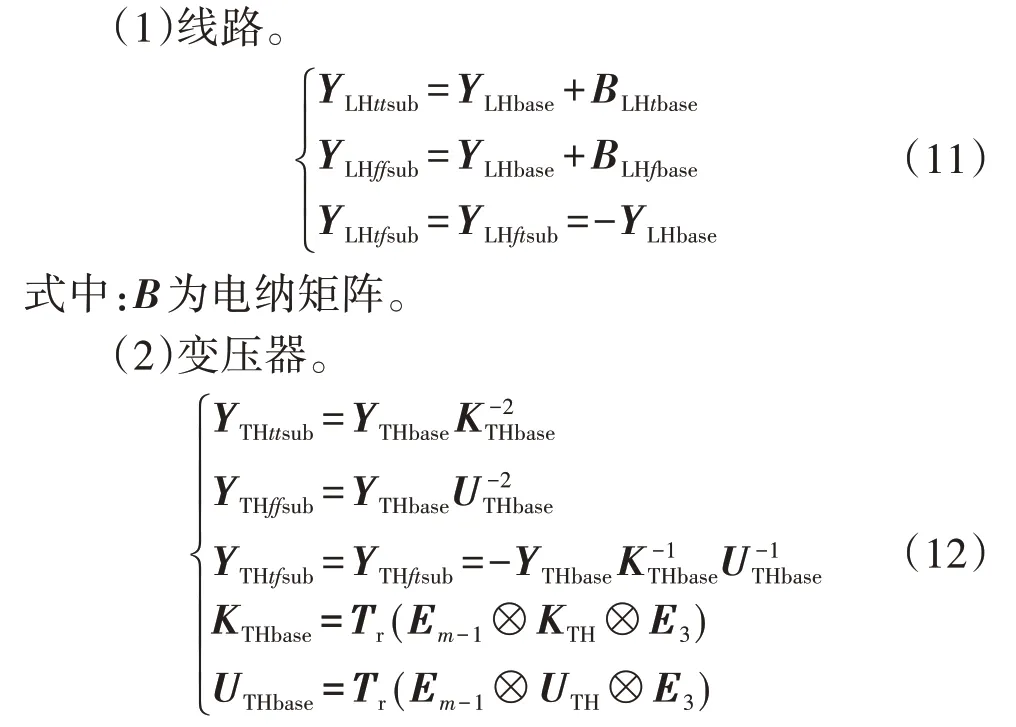
式中：K、U分别为变压器原边、副边分接头变比矩阵。

3）通过构造索引矩阵的方式，将三相谐波子导纳矩阵整合为三相谐波导纳矩阵YH。具体过程如下：

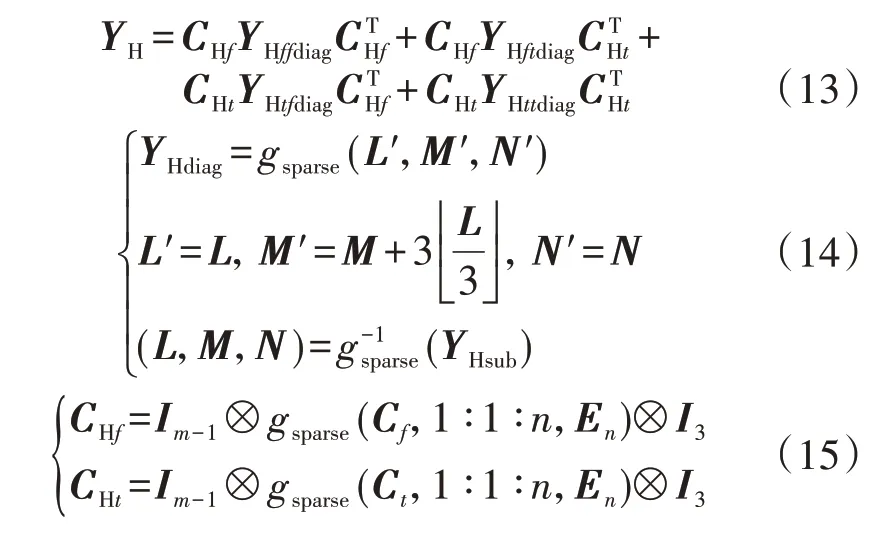
图2 给出了利用本文范型生成三相导纳矩阵的过程。图中：fi、ti(i=1，2，…，n) 分别为第i个元件首、末端节点编号。

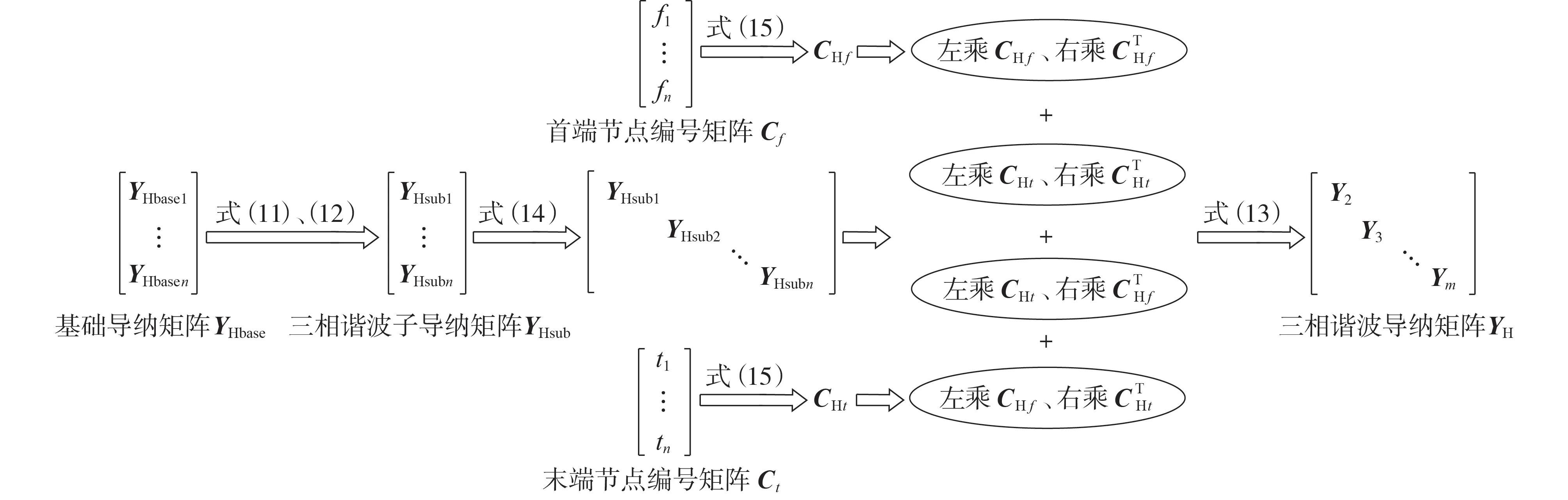
图2 三相谐波导纳矩阵生成图Fig.2 Generation diagram of three-phase harmonic admittance matrix

3 三相谐波潮流过程的实现

3.1 三相谐波导纳矩阵

在具备上述矩阵范型的基础上，生成各种模型的三相谐波导纳矩阵。

1）三相线路谐波导纳矩阵。

首先，构造范型式（8）中的输入矩阵：

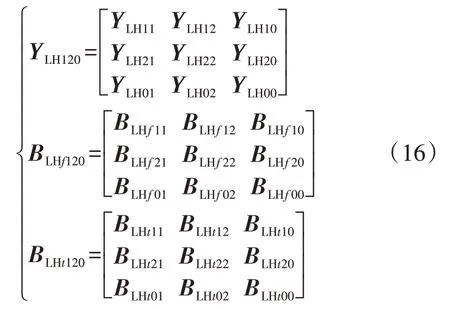
令范型中的n取线路数，由范型式（8）得到三相线路谐波基础导纳矩阵YLHbase，然后由YLHbase推导出三相线路谐波子导纳矩阵YLHsub，再根据范型式（13）即可获得三相线路谐波导纳矩阵YLH。

2）三相变压器谐波导纳矩阵。

由于本文所采用的三相变压器模型无需进行相序转换，因此范型式（8）中的相序转换矩阵可省去。范型式（8）中的输入矩阵为：

令范型中的n取变压器数，由范型式（8）得到三相变压器谐波基础导纳矩阵YTHbase，然后由YTHbase推导出三相变压器谐波子导纳矩阵YTHsub，再根据范型式（13）即可获得三相变压器谐波导纳矩阵YTH。

3）三相负荷／发电机谐波导纳矩阵。

由于本文不考虑负荷与发电机之间的相互影响，其对应的三相谐波导纳矩阵是对角矩阵，可以直接得到三相负荷谐波导纳矩阵YSH和三相发电机谐波导纳矩阵YGH，无需利用范型。

3.2 牛顿-拉夫逊三相基波潮流

牛顿-拉夫逊潮流计算的基础方程形式为：

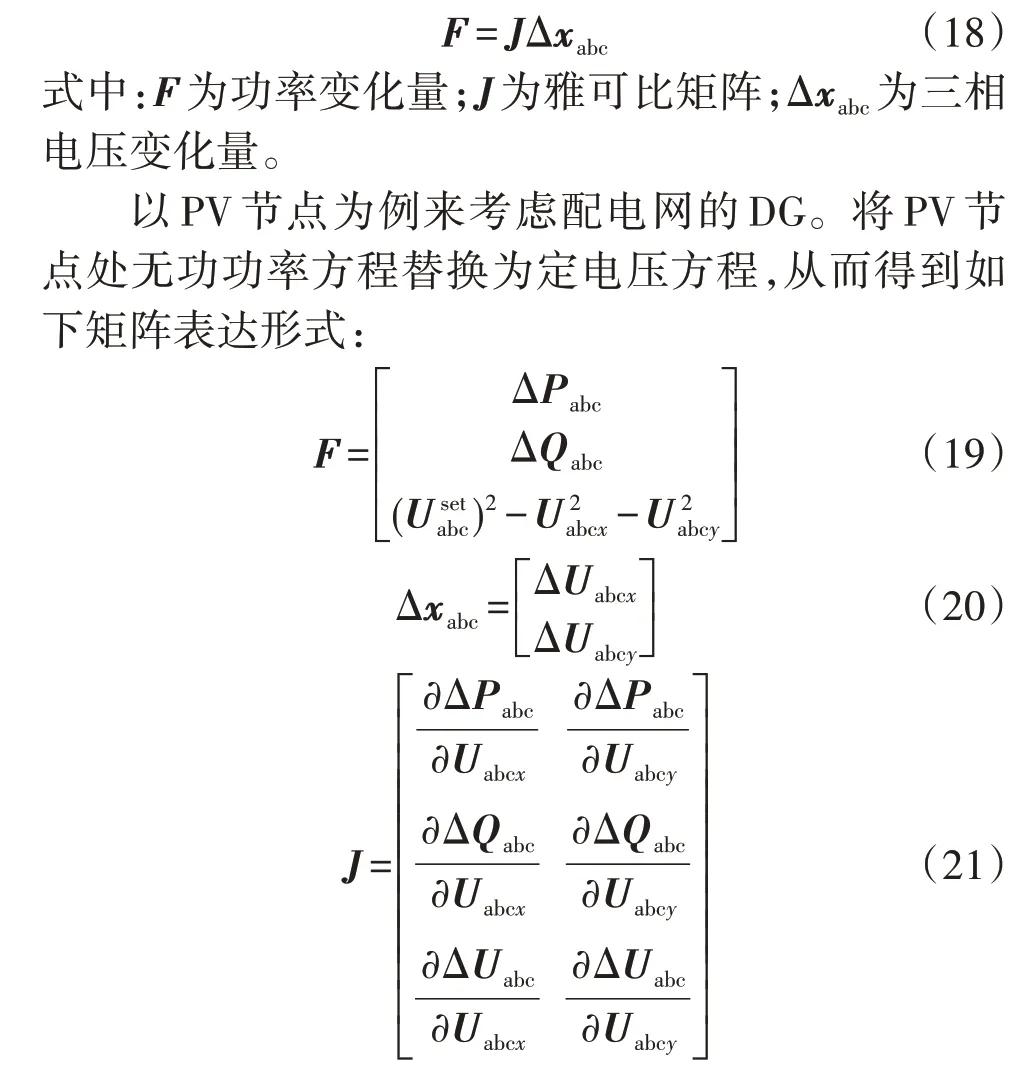
式中：U为电压，上标set 表示设定值，下标x表示实部，下标y表示虚部；P为有功功率；Q为无功功率；Δ表示差分。

3.3 谐波潮流算法

本文谐波源采用的是谐波电流含有率模型，谐波源相角、幅值与基波相角、幅值的关系参考文献［7］。谐波部分的算法使用交替迭代法，可将基波和谐波潮流分开交替求解，即求解基波潮流时以上一次迭代的谐波潮流结果为边界条件，求解谐波潮流时以上一次迭代的基波潮流结果为边界条件，并基于功率守恒原理实现基波和谐波潮流的交替迭代。具体步骤如图3所示。

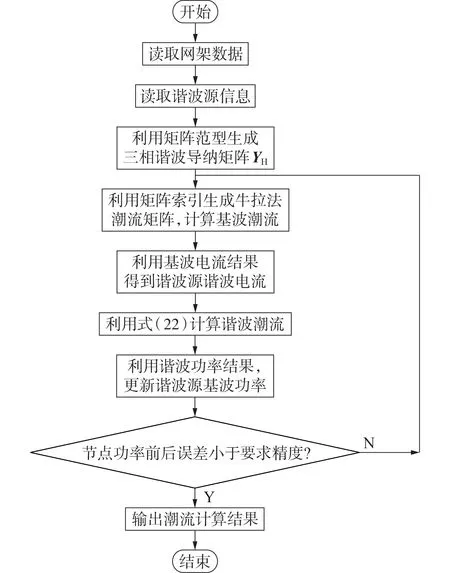
图3 三相谐波潮流算法流程图Fig.3 Flowchart of three-phase harmonic power flow algorithm

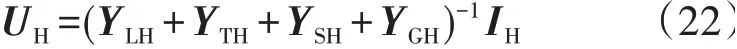
式中：IH为谐波三相电流列向量。

4 算例分析

4.1 有效性验证

本节以IEEE 14 节点系统为例，在节点7、14 接入如表1所示的非线性负荷，即谐波源H1和H2，接线如附录A 图A1 所示，对应的电流频谱如表2 所示。仿真软件为MATLAB 9.5，硬件为CPU inter（R）Core（TM）i7-8750H、8 GB内存。

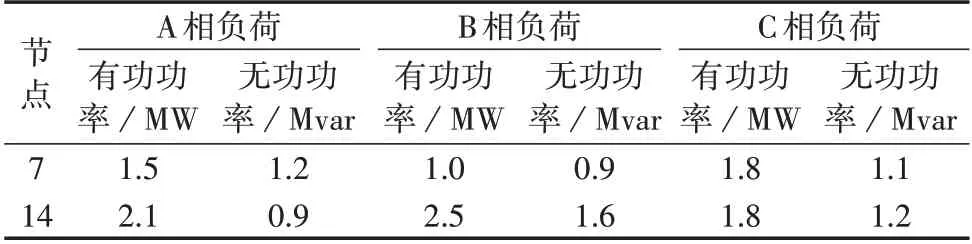
表1 非线性负荷节点信息Table 1 Bus information of nonlinear loads

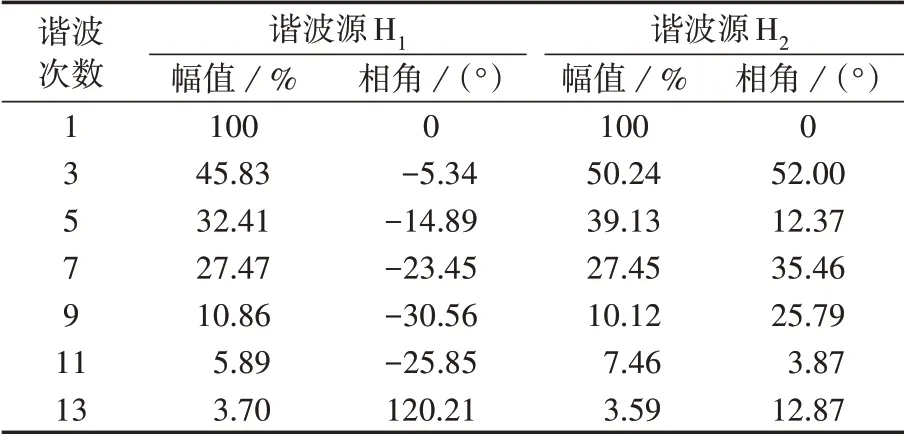
表2 2种谐波源的电流频谱Table 2 Current spectra of two harmonic sources

为了验证本文三相谐波潮流计算结果的准确性和有效性，分别用本文算法和OpenDSS 进行对比计算。潮流收敛精度取为10-10，将本文矩阵范型中的线路元件数n设置为13，最大谐波次数m设置为13，得到线路的三相谐波导纳矩阵，再结合谐波源电流频谱即可计算三相谐波潮流。限于篇幅，算法范型实现的中间过程如附录B 所示，各节点三相电压的总谐波畸变率（THD）如图4 所示，以节点13 为例，2种算法的三相谐波电压如图5所示。

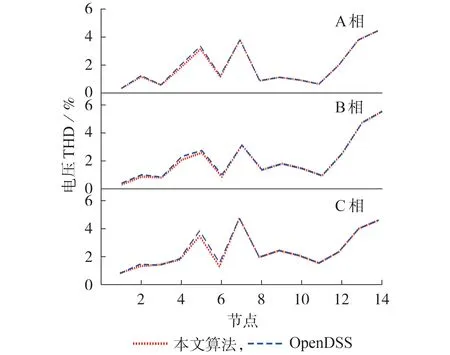
图4 本文算法与OpenDSS三相电压的THD计算结果对比Fig.4 Comparison of THD calculation results for threephase voltage between proposed algorithm and OpenDSS

图5 节点13谐波电压结果对比Fig.5 Comparison of harmonic voltage for Bus 13

由图4和图5可以看出，本文算法计算得到的谐波电压和电压THD 的偏差（电压THD 的平均相对偏差为2.83%，谐波电压平均相对偏差为4.07%）均在合理范围内，满足工程需求，验证了本文算法的准确性与有效性。算法计算结果的细微差异主要源于本文在元件模型、计算精度上与OpenDSS存在差异。

4.2 算法对比

本节在IEEE 123 节点系统中对本文算法与传统前推回代法进行比较，潮流收敛精度取为10-10。为了验证本文算法的计算性能，设置3 种不同运行方式进行对比，不同方式所对应的负荷功率情况如表3所示，2种算法结果对比如图6所示。

表3 IEEE 123节点系统不同运行方式的负荷功率情况Table 3 Load power situation of IEEE 123-bus system under different operation modes

由图6 可知，随着负荷增大，本文算法的迭代次数和运行时间几乎维持不变，而传统前推回代法的迭代次数和运行时间均有不同程度的增长。这是由于牛顿-拉夫逊法采用的是完整的梯度信息，而前推回代法采用的是近似的梯度，搜索效率相对低下。此外，在重负荷情况下，由于潮流解接近静态安全极限，梯度的搜索效率必然会下降。由此可见，本文算法具有计算速度快、效率高和收敛性好的优点。

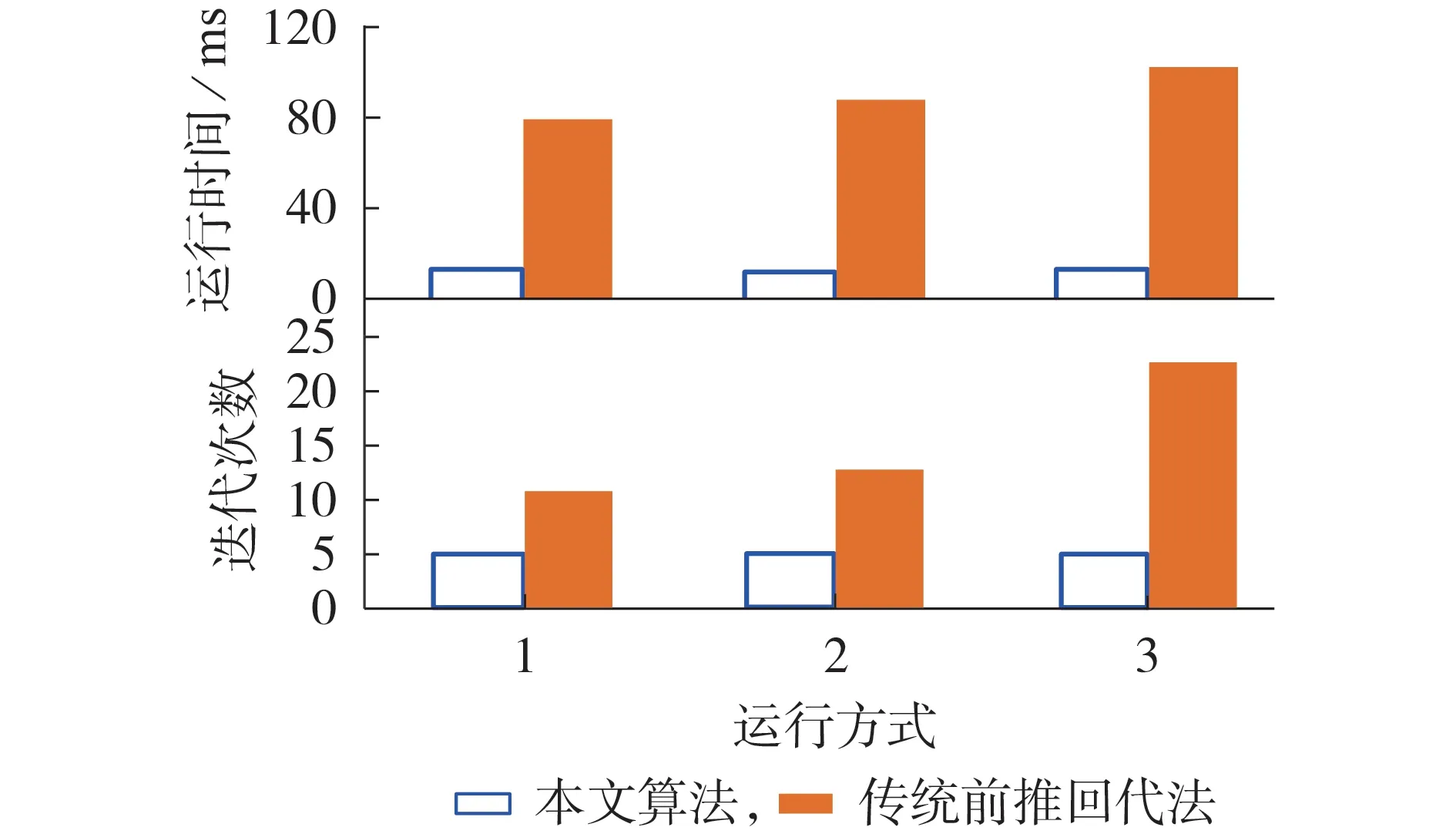
图6 本文算法和传统前推回代法收敛情况对比Fig.6 Convergence situation comparison between proposed algorithm and traditional forward and backward algorithm

在上述IEEE 123 节点系统的基础上，改变系统连接方式，在保持基础连接不变的情况下，连接系统中线路11-27、17-96、36-51、54-94、39-66、119-120、114-122、75-85，构成多个环网，如附录A图A2所示。由于传统前推回代法不具备计算环网的能力，仅给出本文算法的收敛情况，如表4所示。

表4 具有环网情况下的收敛情况Table 4 Convergence situation in case of ring network

由表4 可知，在存在环网的情况下，本文算法的收敛时间与迭代次数与正常情况下相比几乎不变，说明本文算法有较好的处理环网的能力。稳定的迭代次数和较短的运行时间得益于本文矩阵范型较高的运行效率和牛顿-拉夫逊法自身的特性。

由以上算例可知，由于本文算法是基于牛顿-拉夫逊法和散列映射原理构建三相谐波潮流的网络模型，因此算法在环网和放射型网络下的处理效率是相同的。此外，由于本文算法的潮流计算时间为ms级，因此，即使在配电网拓扑结构的频繁切换过程中，本文算法的收敛性和速度仍可以得到保证，在工程实际中具有广泛应用的潜力。

5 结论

本文提出基于牛顿-拉夫逊法并按照矩阵范型运算的三相谐波潮流新算法，该算法保留了牛顿-拉夫逊法二次收敛的稳定性，适用于所有电网结构和运行方式，得到如下结论。

1）基于各序网络独立的原理以及矩阵范型的思想进行算法设计，实现了三相谐波潮流仿真的快速开发和高效计算。将各序网络用矩阵范型的方式进行描述，并充分运用多重索引矩阵等技术，极大地降低了相应算法的复杂性。

2）基于面向矩阵运算的算法，新设备模型的扩展可以通过矩阵以及向量叠加的方式实现，该方式灵活方便，且可以充分运用成熟的矩阵计算程序实现程序的速度优化。

3）算法兼容树形网络和环形网络，能快速适应目前日益复杂的配电网仿真。

笔者后续将尝试采用并行计算方式进一步提高本文算法的效率。

附录见本刊网络版（http：//www.epae.cn）。