低通滤波器对时延耦合振子系统振幅死亡的影响

刘维清，刘汉昌,朱云，许海燕

(1.江西理工大学 理学院,江西 赣州 341000;2.赣南卫生健康职业学院,江西 赣州 341000)

自然界许多系统可以用耦合非线性振子来描述,虽然组成系统的每个个体具有各自的振荡节律,但通过各种形式的相互作用后,耦合振子系统可以表现出有丰富的自组织动力学行为,如各种形式的同步[1-3]和振幅死亡[4-5].其中耦合振子系统的振幅死亡现象对理解生命节律、工程减振、斑图结构形成和系统老化具有重要的意义.

耦合振子系统的振幅死亡是指相互作用的振子系统，由于个体间存在频率失配[6]或耦合作用信号传递产生的时间延迟[7]或耦合通道的响应特性[8-9]等因素影响下而停止振动的现象.有证据表明神经退行性疾病的产生与互相耦合作用的神经元的振幅死亡密切相关[10]，且可以通过压制某些不利的振荡态来控制治疗这些疾病[11].自从瑞利勋爵[12]首次观先察到管风琴的相邻管子会因相互作用而出现消音现象以来,人们在许多耦合振子系统中(如生物系统[13],化学系统[14],激光系统[15],工程系统[16])观察到振幅死亡现象.耦合振子系统振幅死亡的产生条件不仅受系统之间的频率失配的空间分布影响[17-18],还受耦合作用的不对称性[19]和网络结构的影响.在规则网络[20]、随机网络[21]和无标度网络[22]中,耦合系统走向振幅死亡的过程和条件均有所不同.此外,耦合作用的信号传递通道的特性对振幅死亡也具有显著影响.耦合通道的特性主要有幅频特性和相频特性.耦合通道的相频特性中,信号通道对所传递信号产生的时间延迟会导致耦合系统由振荡态走向振幅死亡态[23].邹为等人[24]发现部分耦合通道存在时间延迟有利于促进振幅死亡.在排斥耦合中存在时间延迟时,耦合系统会从振荡态走向振幅死亡态.耦合通道的幅频特性[25]对振幅死亡的稳定性有较大的影响.当耦合通道具有低通滤波特性时,会抑制频率高于某一临界值的信号,从而对耦合振子系统的动力学行为产生影响[26].如在平均场耦合作用下,具有不同截止频率的低通滤波器会使系统从振荡态过渡到各种形式的振幅死亡[27].同时低通滤波器也可以使耦合振子系统产生振荡态与振荡死亡态共存现象.而在时延系统中,对自反馈信号引入低通滤波特性的通道后,可以使耦合振子的振幅死亡区域减小甚至消失[28].低通滤波器是否可以使有时延的耦合系统的振幅死亡区域增大?为了弄清这一问题,以时延耦合朗道周期振子为模型,考虑耦合通道的低通滤波特性对耦合振子系统动力学的影响.结果表明,当耦合振子系统的耦合通道具有低通滤波特性时,其截止频率的减小有利于耦合振子系统走向振幅死亡.

1 模 型

为了更好地研究耦合通道的滤波特性对耦合时延系统振幅死亡的影响,引入耦合朗道振子模型为研究对象

(1)

其中，j=1,2，k=1,2表示耦合振子数，且j≠k,Zj(t)=xj(t)+iyj(t)为振子j的复变量，ε为振子之间的相互作用强度，τ为耦合通道的时间延迟量,α-1为低通滤波器的截止频率,Sk(t)为耦合通道对Zk(t)进行滤波后的输出信号.滤波器对频率低于α-1的信号会进行抑制.ωj为振子j的振荡频率ωj，对于给定不为0的频率ωj，单个子系统会以频率ωj作周期振荡.当通道不存在滤波特性时,即(α=0)时,Sk(t)=Zk(t).

2 理论分析

为了研究耦合通道的滤波特性对有时延的耦合振子振幅死亡的影响，先考查耦合振子系统固定点(0,0)的稳定性.令Z1=Z2=0,S1=S2=0， 并引入微扰量ξi，则微扰的动力学演化可由其特征方程

(2)

确定.考虑2个全同耦合振子，有ω1=ω2=ω，方程(2)可化简为

(1+iω-ε-λ)(α-1+λ)=±α-1εe-λτ.

(3)

特别地，当α=0时，截止频率趋向于无穷，可以看成是耦合通道对通过其的信号Zj没有滤波作用.此时，耦合振子的特征方程[7]可以写成

1+iω-ε-λ=±εe-λτ.

(4)

振幅死亡域对应于方程(4)中实部小于0的特征值λ，所以令λ的实部为0可得振幅死亡与振荡区域的临界线

(5)

振幅死亡区域为(5)式中2曲线所围区域.若2曲线不相交，则耦合振子系统在此参数下不存在振幅死亡.在振子振荡频率为ω=4时，τ～ε参数空间中实线τa和虚线τb没有共同的区域，所以耦合系统在此频率下没有振幅死亡岛，不存在振幅死亡现象如图1(a)所示.

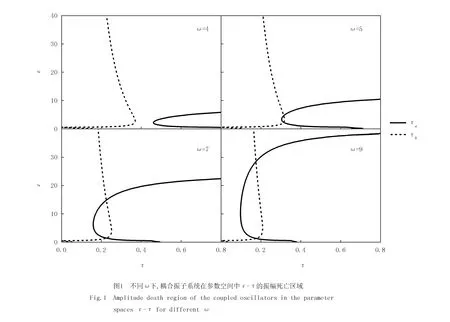
当α≠0时，耦合通道存在低通滤波特性，此时耦合振子振幅死亡区域的临界线可由方程(3)中使特征值实部等于0得到.由于该方程是超越方程，无法得到解析的结果，可通过数值计算得到滤波器具有不同截止频率时的振幅死亡区域.

3 耦合通道滤波特性对耦合时延系统振幅死亡岛的影响

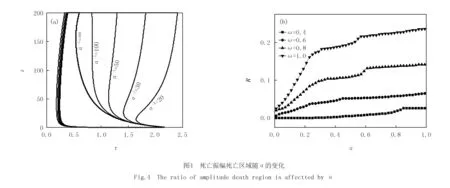
为了探讨耦合通道的低通滤波特性对时延耦合振子系统的振幅死亡区域的影响，分别计算振荡频率为ω=7,9时，通道的低通滤波器的截止频率α-1=30,40,60,80,在参数空间(τ,ε)振幅死亡岛的区域.如图2(a,b)可知，随着低通滤波器的截止频率减小，与没有低通滤波器通道时的振幅死亡岛相比(粗实线所围区域)，振幅死亡岛的面积逐渐增加.因此，通道的滤波特性有利于耦合振子的振幅死亡.

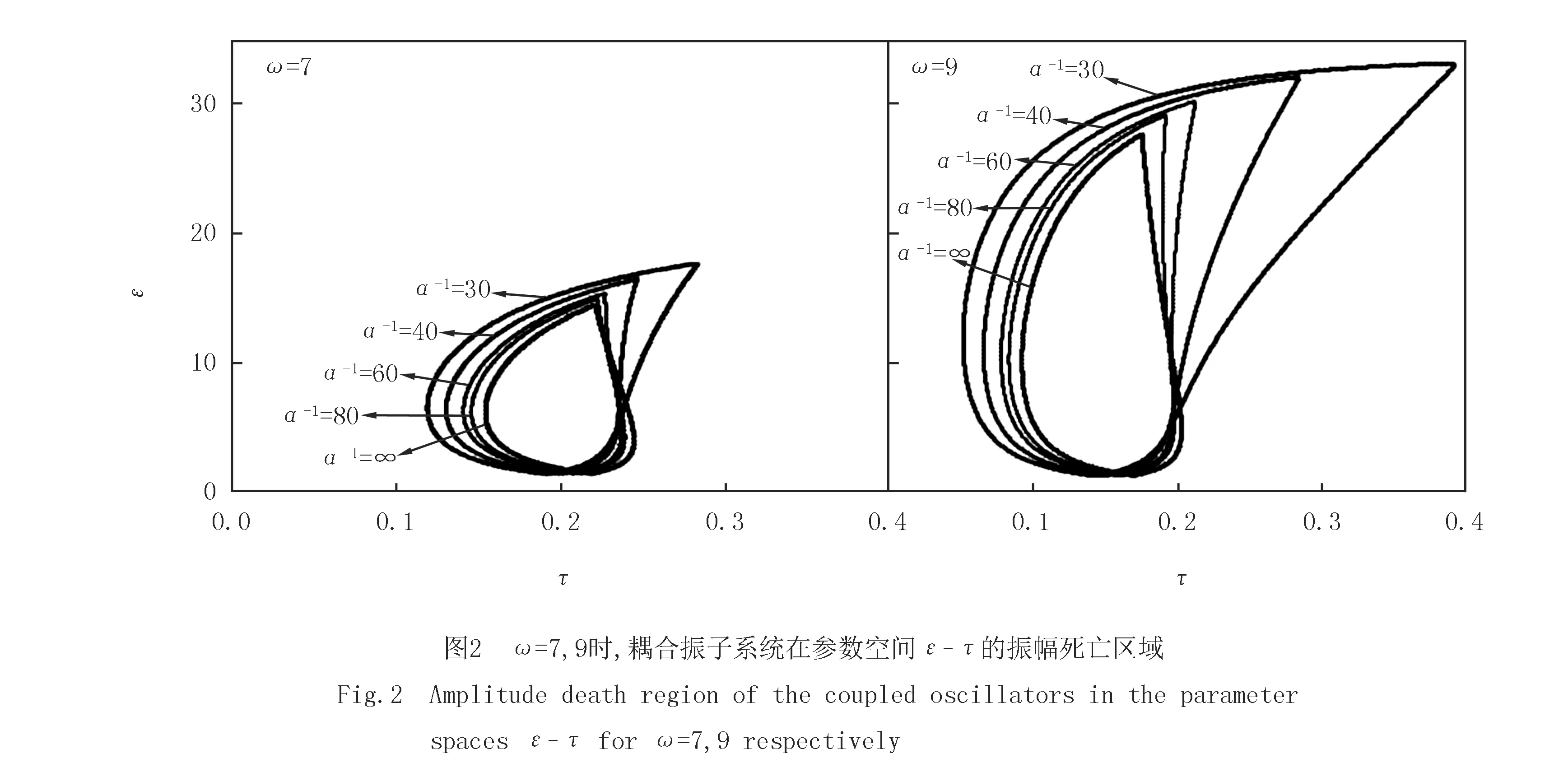
为了更好地确定耦合通道的低通滤波器的截止频率对振幅死亡岛的影响，引入了归一化参量R=S(α)/S0；其中S(α)表示低通滤波器的截止频率为α-1时，振幅死亡岛的区域面积，S0表示参数给定的参数范围τ∈[0,0.9],ε∈[0,35]的区域总面积.在不同振荡频率下，R和α的函数关系如图3所示.结果表明，对于具有不同振荡频率的振子系统，振幅死亡岛的面积会随着低通滤波器的截止频率α-1的减小先快速增加，然后缓慢增加至某一稳定值.频率越大，最终稳定的死亡区域面积越大，且达到稳定值所需的截止频率α-1越大.注意到当ω=3时耦合振子系统在无通道滤波器时不存在振幅死亡现象，而加入通道滤波特性后，随着截止频率α-1减小到3.32时才开始出现振幅死亡岛.因此，低通滤波器有利于2个耦合时延振子产生振幅死亡.值得注意的是邹为等人[28]发现通道的低通滤波器截止频率减少有利于促进耦合振子振荡，减小振幅死亡区域.其低通滤波器是对自反馈的信号进行滤波，而本文中的低通滤波器是对来自耦合振子的信号进行滤波，在实际耦合系统中更具普适性.

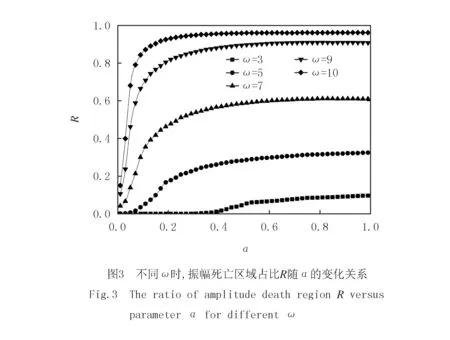
4 时延混沌振子中滤波器对振幅死亡岛的影响

为了进一步研究耦合通道低通滤波器对时延耦合振子系统振幅死亡的影响的普适性，考查耦合混沌振子系统，以耦合Rössler振子系统为例，

(6)

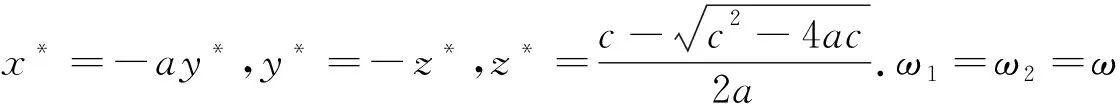
没有时延和通道滤波特性时，耦合全同混沌振子会随着耦合强度的增加而走向完全同步态.当耦合通道只存在时间延时而无低通滤波特性时，耦合系统会在参数空间(τ,ε)存在振幅死亡区域如图4(a)中的粗实线所包围区域.耦合通道同时存在时延和低通滤波特性时，随着滤波器的截止频率α-1减少，耦合振子系统的振幅死亡区域增加.随着截止频率α-1的减少，振幅死亡区域先快速增大，然后缓慢增加，且单个振子的振荡频率越大，振幅死亡区域的面积也越大，其变化规律与前面耦合周期振子的结果相似.与耦合周期振子的情形不同的是，截止频率较小时，耦合振子的振幅死亡岛的面积才趋于稳定值.

5 全联通网络中滤波器对振幅死亡岛的影响

为了研究耦合通道的滤波特性对振幅死亡影响的一般性，进一步讨论耦合全连通网络.简单起见，以N=3为例，讨论全连通耦合网络模型中的朗道振子振幅死亡现象.

(7)

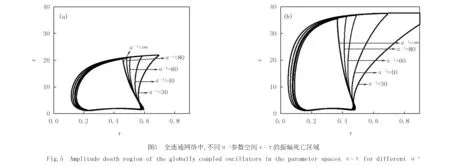
其中，Sk(k=1,2,3,…,N)为低通滤波器，当耦合通道没有滤波器时，耦合振子在参数空间(τ,ε)的振幅死亡岛在ω≥4时才存在.分别以ω=7,9为例，通过数值计算分别得到滤波器在不同的截止频率α-1=30,40,60,80时耦合振子在参数空间(τ,ε)的振幅死亡岛如图5(a,b)中细实线所包围的区域.其中粗实线所包围区域为无低通滤波器时的振幅死亡岛.结果表明，耦合全连通网络中，随着通道滤波器的截止频率α-1减小，振幅死亡岛面积逐渐增加.且初始频率ω越大，振幅死亡岛的区域也越大.

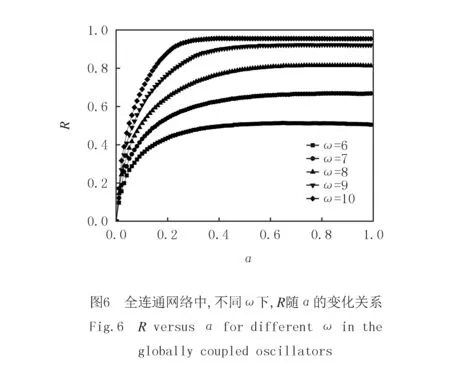
同样地，由归一化参量R与α的关系图6可以看出，随着α的增加，振幅死亡区域先快速地增加，然后缓慢增加到某一稳定值.该稳定值随着单个振子的频率ω的增加而相应地增加，此外，ω越大趋向于稳定所需的α值越小.因此，在全连通网络中低通滤波器的截止频率对振幅死亡岛的影响规律与2个耦合振子系统的结果相似.

6 结 论

耦合振子系统的通道特性对耦合振子系统的振幅死亡具有显著的影响.低通滤波效应越强，越有利于促进耦合振子的振幅死亡.此规律在耦合周期、混沌振子系统，局域耦合和全连通耦合系统均具有普适性.因耦合通道的滤波特性在工程中具有普适性，对耦合振子系统动力学的影响规律可为工程中系统的减振，生物节律的控制提供理论支持.此外滤波器结构简单，易于实现，因此局部滤波器方案在实验上具有可行性，可以应用于非线性电路、混沌控制、耦合激光器和神经系统等.