随机需求下半开放式冷链物流车辆路径优化
李想,闵德权,张祺
工艺与装备
随机需求下半开放式冷链物流车辆路径优化
李想,闵德权,张祺
(大连海事大学 交通运输工程学院,辽宁 大连 116026)
降低冷链物流配送成本的同时,保证客户体验及碳排放达到企业要求。综合考虑运输距离、客户软时间窗约束、碳排放、生鲜变质等因素,以制冷成本及对配送时间惩罚成本在内的总成本最低、碳排放量最低、生鲜产品新鲜度最高为目标,建立多目标生鲜配送路径优化模型,并设计模拟退火算法,以北京某冷链物流企业为例进行求解验证。得出生鲜配送方案,通过配送模式对比表明多中心半开放式在降本和缩短路径长度方面更具优势,其中运输总费用和车辆行驶总距离相比于单中心独立配送模式分别降低了8.41%和36.36%。需求不确定下,合理决策路由可在达到企业对生鲜产品新鲜度及碳排放标准的同时,有效降低配送成本。
冷链物流;路径优化;半开放;不确定需求;随机规划;模拟退火
近年来,随着消费者生活水平的提高和消费观念的转变,生鲜产品冷链物流发展迅速,物流配送规模急剧扩大,小范围的单配送中心配送模式逐渐向多中心模式转变,这对物流企业的配送过程提出了更高的要求。在2020年,由于新冠疫情的突然发生,“冷链”、“冷链运输”、“骨干冷链物流基地”等关键词获得了全社会的空前关注。为确保易腐食物的新鲜度,在整个运输过程中需要进行低温控制,加之生鲜产品的自身特性,导致实际需求量的不可预测性,使得企业在对生鲜冷链运输的路由决策提出了更高的要求。
生鲜配送导致温室气体排放量的增加,环境保护、节能减排等问题受到国际社会的高度重视。碳税作为一种有效的政策工具和环境保护的重要标准,已经被引入到节能减排中,这使得物流企业的配送成本有所上升,因此,在保证产品新鲜度的同时减少环境污染,实现低碳绿色运输,是当今社会中不可避免的问题。故在构建冷链物流路径优化模型中,仅以降低配送成本为目标是远远不够的,生鲜品到货时的新鲜度以及冷藏车在运输环节产生的碳排放也要考虑其中。为了高效解决在配送生鲜产品期间由于冷链配送以及市场需求波动所引起的碳排放和成本问题,文中建立多个目标下的针对冷藏车路由决策的优化模型,利用启发式智能算法进行求解,让冷链配送路线趋于合理。
长期以来,学者对车辆路径问题(Vehicle Routing Problem, VRP)做了大量研究,该问题针对不同标准可拓展为多种子问题,例如,配送中心多于一个,即多配送中心路径优化问题(MDVRP),加入时间窗约束,即带时间窗的MDVRP(MDVRPTW)。在配送模式上又可分为闭合式、开放式和半开放式。文中所研究的即为生鲜品带时间窗的多中心半开放式路径优化问题(Multi-depot Half Open VRP with Time Windows, MDHOVRPTW)[1],与此同时考虑客户满意度和碳排放,即MDHOVRPTW-CSC(Multi-depot Half Open VRP with Time Windows for Cold Chain Logistics Considering Customer Satisfaction and Carbon Emissions)。Adelzadeh等[2]采用双目标规划,以运输距离最小化以及最大化客户服务等级为目标,建立具有不同车辆类型的MDVRPTW模型,利用模拟退火算法求解并应用到ISACO公司实例当中,验证了方法的有效性。刘家利等[3]在模型中加入了商品间的互斥性以及商品与车型间的匹配性等因素,并设计了两阶段自适应遗传算法进行求解,验证了模型的可行性。范厚明等[4]设计了蚁群算法求解联合配送模式下的VRP问题,考虑到生鲜运输时效性要求,设计了相应时间窗及惩罚成本,实验表明该模型可快速对客户需求做出反应,降本的同时有效提高配送效率,从而减少生鲜品的损耗。
从以上的研究可看出,基本以实现最低成本为目标,而不考虑顾客满意度和环境因素。Li等[5]针对冷链物流的绿色车辆路径问题,在模型中加入了产品新鲜度和温室气体排放等因素,结果表明考虑全套的温室气体可以有效降低总成本。Qin等[6]同时考虑了成本、顾客满意度和碳排放,设计了循环进化遗传算法对模型进行计算实验,结果表明碳排放和客户满意度之间存在权衡。Wang等[7]建立了一个碳交易策略下具有混合时间窗的冷链第三方物流服务商(3PL)的低碳两级异构车队车辆路径问题模型,研究表明,客户满意度是影响企业规划车辆路径策略的关键因素。
近年来,出现了大量考虑随机需求的VRP问题。Cao等[8]研究了需求不确定的开放式车辆路径问题,提出了一种改进的差分进化算法来求解在特定有界不确定性集中以运输成本和未满足需求最小化为目标的鲁棒优化模型,提出鲁棒优化可极大避免未满足需求,同时产生较小额外成本。Moghaddam等[9]提出了一种改进的粒子群优化算法来求解需求假定为不确定且分布未知的VRP问题,并通过对比分析验证了算法的有效性。管峰等[10]研究了需求不确定且有容量限制的VRP问题,采用鲁棒优化模型求解,提出该模型在需求波动下可有效保证路径的可行性。邓烨等[11]将客户需求量视为随机变量,设置时间窗构建机会约束模型,最后等价转为确定性模型求解。杨翔 等[12]采用三角模糊数定量刻画模糊需求,设计了两阶段禁忌搜索算法来求解MD-OVRP问题。Hu等[13]研究了在需求和行程时间不确定性下具有硬时间窗的车辆路径问题,设计了一种基于改进的自适应可变邻域搜索启发式的两阶段算法进行计算实验,结果表明该算法可保证车辆数以及总行驶距离不增的情况下得到高质量的鲁棒解。
随着我国三方物流业的发展,配送资源的整合是未来生鲜电商的发展趋势,低效的道路运输造成了不必要的成本和污染排放,这个问题在冷链配送过程中更加严重,因为在冷链运输中,温度控制是为了保证产品的质量,因此,文中提出基于时间窗的多中心联合配送模型,以提供一条环保、低成本的配送路线。该模型考虑了生鲜物流的大部分因素,相较于传统单配送中心独立配送模式,具有效率高、损耗少和服务水平均衡等优势,并使冷藏车和冷库设施等资源得以充分的利用。
1 问题描述及条件假设
1.1 问题描述
冷链物流除了要在恰当的时间以合理的运输方式将生鲜产品交递给需求者,更要给需求者带来最优质的服务[14]。随着近年来可持续发展战略的提出,我国企业纷纷将发展目标转向了低碳环保和顾客体验,所以在构建冷链配送路径优化的模型中加入这2个因素将成为必然。
文中所研究的MDHOVRPTW-CSC问题可描述为:存在多个配送中心,需求点数量已知,但每个需求点订单的需求量未知,每个配送中心有一组负载能力已知的冷藏车。由于需求点的不同,所对应的客户对生鲜品的到达时间要求也有所差异,这就对冷藏车配送方案的合理性提出了较高要求,保证在客户可接受的时间范围内完成配送。在降低总成本的同时,也要满足对客户满意度和碳排放的要求。物流配送模式见图1。

图1 半开放模式下物流配送模式
1.2 条件假设
在生鲜食品冷链物流配送过程中,存在诸多不可控的因素,故而为了简化模型的同时便于计算,文中在不影响模型求解结果,以及规划结果的前提下提出以下几点假设。
1)车辆一旦出发执行配送任务,其服务的客户信息和配送顺序已知,不会出现新的客户或中途指派等突发情况。
2)文中只考虑单纯送货情况,无取货任务。
3)配送网络拥有多个不同位置的配送中心,每台冷藏车均需从配送中心出发,在完成相应指派任务后,可择优选择配送中心进行停靠,不要求返回原配送中心。
4)初始设定的行车路线畅通可行,车辆行驶速度保持不变,不考虑运输过程中室外温度变化。
5)对于不同类别生鲜品,其适用模型以及变质规律不同,故文中考虑的生鲜种类及配送车型均为单一类别,已知冷藏车的负载、油耗以及制冷性能等数据。
6)运输总费用中暂不考虑生鲜产品的库存费用和装卸损耗,此外,每个客户的服务时间固定。
7)客户需求量视为随机变量,且服从正态分布,并且各服务点的需求相互独立[15],配送中心拥有充足存储量以满足客户需求。
2 数学模型
2.1 问题分析并公式化
2.1.1 总成本
文中所构建关于冷链物流的数学优化模型中目标函数所考虑的成本因素除了普遍的车辆运输以及派遣成本外,还包括了冷藏车制冷能耗成本以及因生鲜货物未在客户规定时间内送达所产生的时间惩罚成本。
1)车辆使用成本。

2)运输和制冷成本。冷链物流的特性之一就是易腐性,因此为了保证生鲜食品的货物质量,就要求整个配送过程中让产品始终保持低温状态,在此过程中为了保持车厢温度恒定而必须持续消耗能源,由此而产生的能耗成本即为制冷成本。这部分的成本分为2个过程,首先是在运输过程中所产生的距离成本,以及为保证车厢内保持恒温而产生的制冷成本;其次,由于卸货过程中由于车门处于敞开状态而与外界产生热交换,故防止车厢内的温度迅速上升,到达客户节点后需根据货物量对冷藏车车厢预冷,所产生的预冷制冷成本。
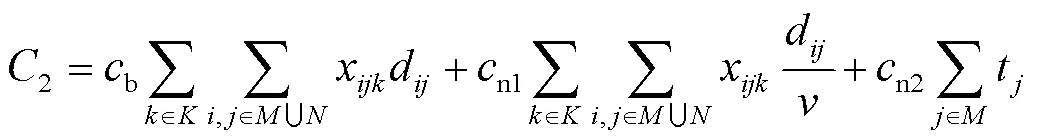


图2 需求点时间窗及惩罚成本


2.1.2 生鲜产品新鲜度
生鲜产品的外表状况即新鲜度,是顾客对产品满意度的重要评价标准。易腐性和时效性等作为生鲜食品的特性,使得新鲜度在很大程度上受货物的配送时长和运输距离的影响。

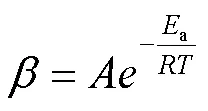

2.1.3 冷链车辆运输碳排放
冷藏车运输期间所产生的碳排放与车辆油耗呈线性关系[17],公式为:
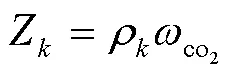
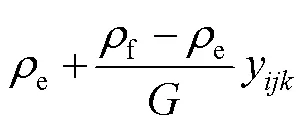

由此可知,冷藏车配送碳排放公式为:
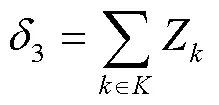
在现实环境中,往往最短距离和最低油耗的配送路线有所差异,虽然车辆的运输距离变长,但具有更合理的负载,进而使得碳排放量有所减少。
2.2 符号说明
2.3 配送路径多目标优化模型
综上所述,随机需求下建立MDHOVRPTW-CSC的数学模型如下。
1)目标函数。
冷藏车配送总成本最小的目标函数为:
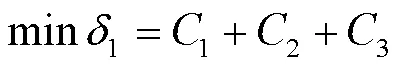
生鲜产品新鲜度最大和冷链车辆运输碳排放量最小的目标函数分别为:
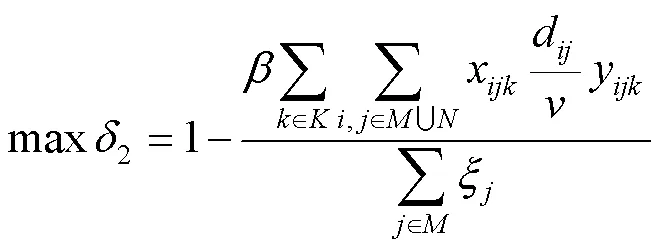
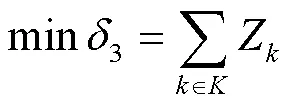
2)约束条件。
确保负责配送车辆数小于已有数量:

冷藏车的负载限制:

满足客户全部需求的概率不小于所设定的置信水平:

每个客户点仅被服务1次:

冷藏车在对某客户服务结束后须前往下一节点:

冷藏车出发后不允许出现未服务客户就返回配送中心的场景:

冷藏车完成指派任务后不必返回原配送中心:

消除冷藏车配送路线中子回路的条件:

运输途中可能由于诸多因素而引起货损,故限制客户需求量小于冷藏车到货实际运量:
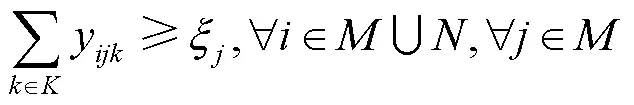
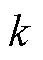


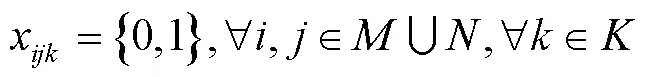
2.4 随机约束转换




综上,随机机会约束(16)可转化为确定约束(28)。
3 算法实现
3.1 主要目标法
求解多目标规划模型一般将多目标优化问题转化为单目标优化问题,所采用的方法以线性加权法和主要目标法为主。文中计划采用主要目标法对模型进行求解,主要目标选取总运输成本最小、生鲜产品新鲜度最大以及碳排放量最小3个目标函数的其中之一,其余2个目标满足一定条件即可。冷链物流企业的战略部署决定了主要目标函数的选择,假如企业更加注重冷藏车的碳排放,那么将碳排量最小作为主目标,而将总配送成本以及客户对生鲜品质满意度作为约束条件,进行数学优化模型的求解,转化方式为:
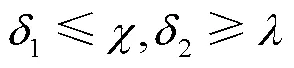
3.2 模拟退火算法
尽管考虑了更多的变量和约束,但所构建的MDHOVRPTW-CSC模型是VRP模型的衍生,计算原理及性质相同。文中采用模拟退火算法(Simulated Annealing,SA)对问题进行求解,因该算法是解决组合优化问题最灵活、最有前途的算法之一,且可以优化不可微或不连续的函数,故该算法处理多目标下的车辆路径优化问题具有一定优势[20]。算法分析步骤见图3。
具体操作步骤如下。
1)文中采用实数编码,负数(−1, −2, −3, …, −)表示配送中心,正数(1, 2, 3, …,)表示客户,例如,代码如−1, 1, 2, −2, −3, 3, 4, −3, 5, 6, −2表示需要3辆车为6名客户服务,具体路线为A-1-2-B、C-3-4-C、C-5-6-B。

图3 模拟退火算法求解流程
4 实例分析
采用模拟退火算法,在需求不确定情况下,分别以运输总成本、生鲜品质新鲜度以及碳排放量为主要目标,其他目标满足一定条件即可。文中实验环境设置为:Intel Core i7-8550U 8 GB,Windows 10专业版,该实例在Matlab R2018a中进行计算。最终得出为线下25家分公司进行生鲜配送的最优规划方案,进而计算出对应方案的总配送费用、生鲜品质满意度以及冷藏车碳排放量,见表2。
从表2中给出的这几组有效解可知,总配送成本、生鲜品质满意度以及车辆碳排放之间存在着效益悖反关系,当运输总费用增加了3.77%,生鲜产品新鲜度下降了1.87%,同时冷藏车碳排放量下降了1.23%,故总费用与其他因素成反比关系。通过结果对比分析看出,以配送总费用为基础考虑生鲜产品新鲜度以及冷藏车碳排放的多目标优化模型,可以让公司根据自身需求,选择相匹配的主要目标对模型进行优化,并且决策者可以更加直观的在不同目标之间进行抉择,由此得出适合本公司的配送方案,因此更加体现出该模型的独有优势。
表2虽然给出在分别满足各目标下的最优解,但均存在某一目标值不满足企业要求的情况,因此为了给出满意解,分别以总成本、生鲜品质新鲜度以及碳排放量为主要目标函数,对该模型进行了多次求解并进行结果对比分析,最终得出同时满足成本、碳排、服务质量的要求的配送方案,见图4,其中菱形、三角形和圆形分别代表从配送中心A、B以及C出发的车辆配送经过的需求节点。配送中心共需16辆冷藏车来完成配送工作,且最优配送路径长度为1 645.32 km。目标函数值即总配送费用随迭代次数的增加而降低,直到达到最佳解21 993.15,运行456次以后总费用已经不再发生变化,结果表明了启发式模拟退火算法在这种情况下的收敛特性。
为了进一步证明文中生鲜产品配送模式及算法的有效性,在相同的假设和系统环境下,以总运输成本为主要目标函数,对该家冷链物流公司进行多模式对比分析。
表1 配送节点及客户需求基础数据
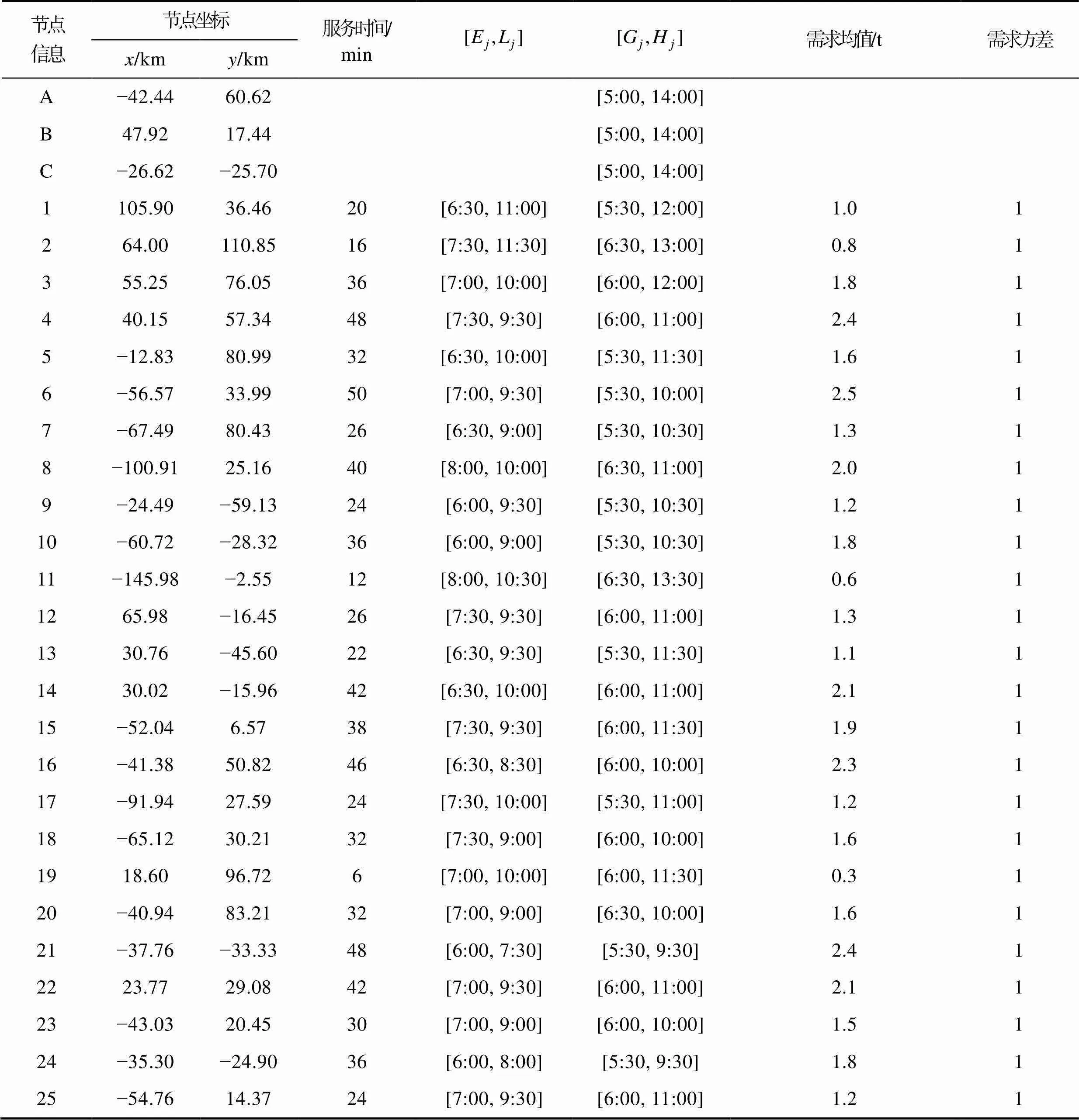
Tab.1 Basic data of distribution nodes and customer requirements
表2 不同主要目标下的结果比较

Tab.2 Comparison of results under different main goals
1)MDHOVRPTW-CSC,即文中所构建冷链物流配送模式,最优配送路径见图5。
2)MDVRPTW-CSC,即不参与联合配送仅执行多中心闭合式配送模式,要求从某一个配送中心出发,完成任务后须返回原出发配送中心。首先使用K-mediods聚类算法[21]对案例数据进行分类处理,并运用文中算法逐一对3个配送中心的路径问题进行求解,最优路径安排见图6。
3)VRPTW-CSC,即单配送中心闭合式配送模式,要求仅使用自有配送中心,且冷藏车始末点均为配送中心,假设点为坐标原点即(0,0),运用文中算法进行求解,最优配送路径见图7,其中四边形表示客户需求点。
在相同系统优化环境下,分别对3种VRP模型运行10次,并将运算结果的均值、最小值及最大值附于表3中,对比多中心闭合模式以及单中心闭合模式,不难看出,配送成本均值分别为22 021.23、22 113.91和24 042.87,文中模型的配送平均总费用分别降低了0.42%和8.41%;配送路径长度均值分别为1 658.19、1 717.30和2 605.75,文中配送模式下分别缩短了3.44%和36.36%的行驶里程。根据结果对比分析可以看出,多中心半开放配送模式能够大幅减少因闭合模式所引起的频繁往返始发中心而产生的多余路径,降低配送费用,生鲜产品配送效率也有了极大地提高,不仅证明了文中模型的经济性,也验证了文中算法的有效性。
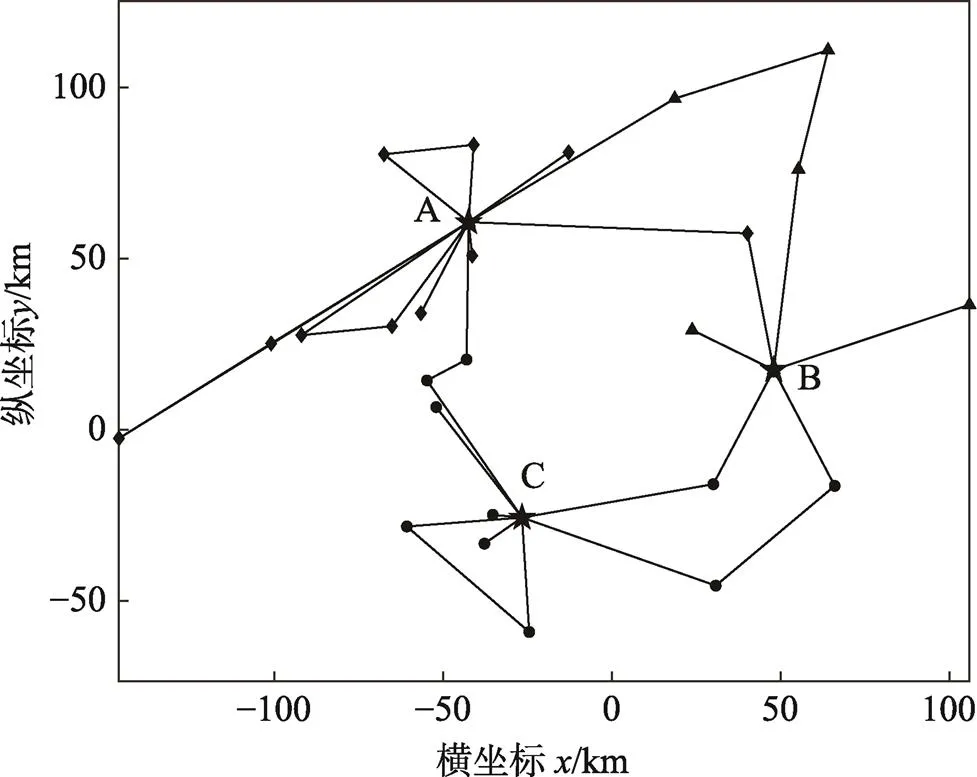
图4 MDHOVRPTW-CSC满意解
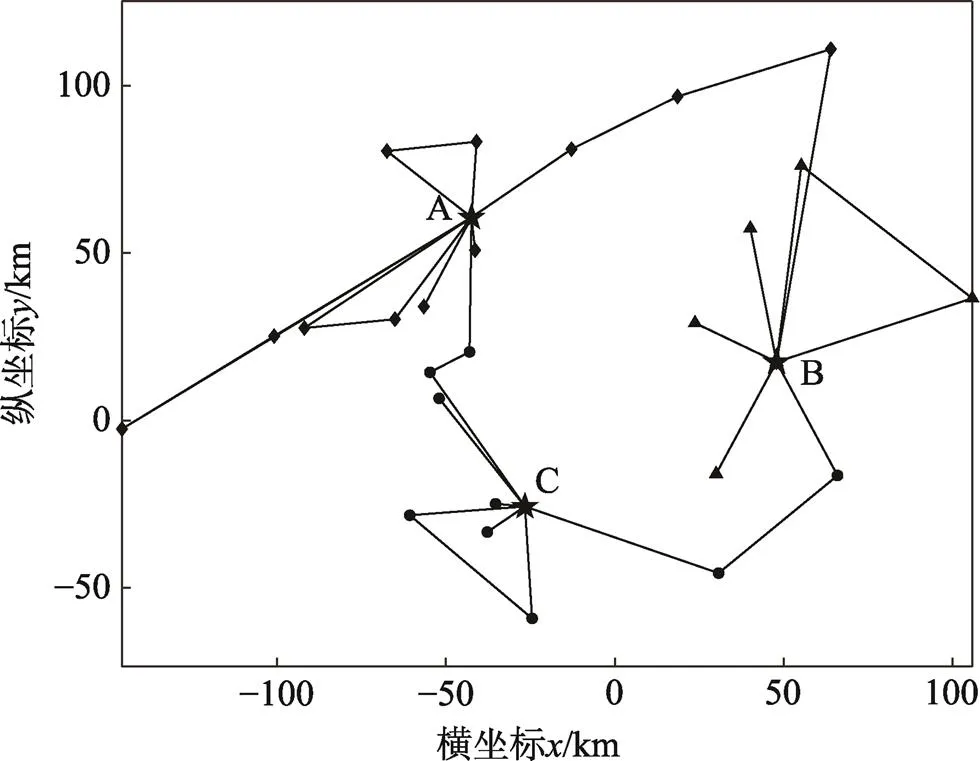
图5 MDHOVRPTW-CSC最优路径
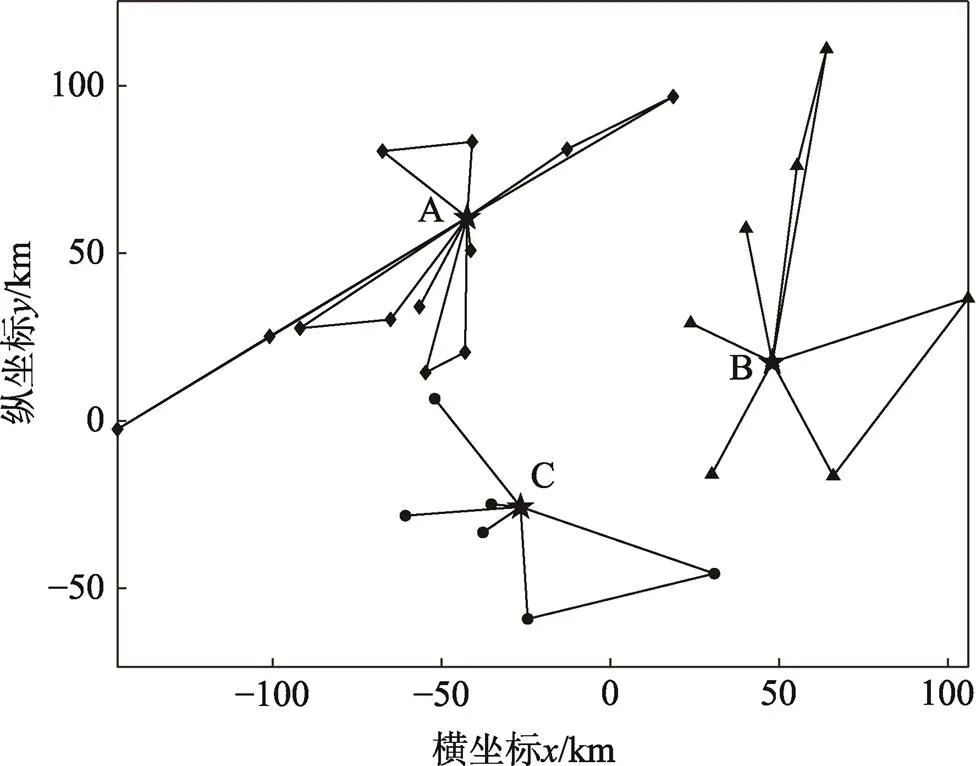
图6 MDVRPTW-CSC最优路径
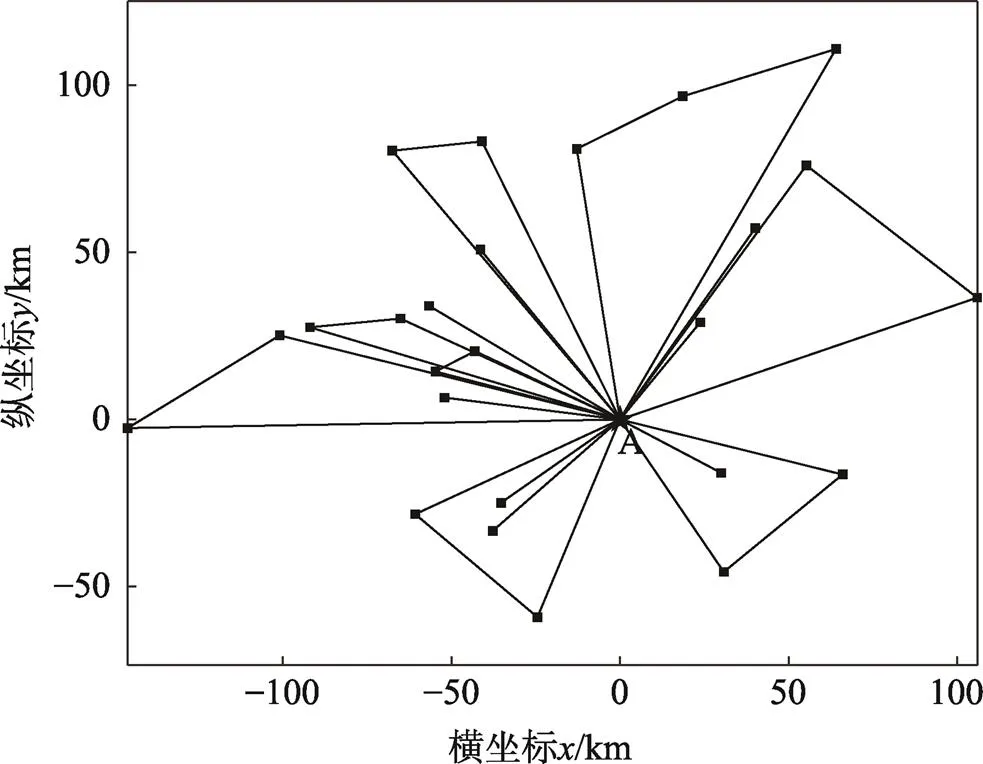
图7 VRPTW-CSC最优路径
表3 不同配送模式下的结果对比

Tab.3 Comparison of results under different distribution modes
5 结语
文中研究了生鲜食品配送行业中一个特殊的车辆路径问题,针对生鲜易腐性和时效性等特点,综合考虑了配送时间、生鲜变质及碳排放等因素,且基于如今单配送中心独立配送不足以满足企业现状,故而建立了不确定需求下的多中心半开放式生鲜配送路径规划多目标模型。利用随机规划思想将随机需求转化为确定约束,使得该模型更具有稳健性,运用模拟退火算法对模型进行求解。最后,使用某冷链物流企业的实例进行多次求解并与闭合配送模式下的单中心和多中心优化方案进行数据对比分析,配送总费用和运输距离均有明显的下降,尤其配送里程缩短了将近1/3,不仅可以减少生鲜品在配送环节的损耗,还能提高客户满意度,提高了整体的服务水平,验证了文中算法及模型的有效性。
文中丰富了生鲜电商配送路径优化模型,为冷链物流的路径规划体系提供了参考依据。在未来考虑碳排放的多配送中心路径优化冷链配送研究中,可以考虑多车型、多温度和多类型生鲜食品的联合配送。
[1] 刘冉, 江志斌, 耿娜, 等. 半开放式多车场车辆路径问题[J]. 上海交通大学学报, 2010, 44(11): 1539-1545.
LIU Ran, JIANG Zhi-bin, GENG Na, et al. The Half Open Multi-Depot Vehicle Routing Problem[J]. Journal of Shanghai Jiao Tong University, 2010, 44(11): 1539-1545.
[2] ADELZADEH M, MAHDAVI ASL V, KOOSHA M. A Mathematical Model and a Solving Procedure for Multi-Depot Vehicle Routing Problem with Fuzzy Time Window and Heterogeneous Vehicle[J]. The International Journal of Advanced Manufacturing Technology, 2014, 75(5-8): 793-802.
[3] 刘家利, 郭秀萍. 存在产品互斥和车辆匹配的多中心开环车辆路径问题[J]. 系统管理学报, 2016, 25(1): 129-138.
LIU Jia-li, GUO Xiu-ping. Multi-Depot Open Vehicle Routing Problem with Exclusive Products and Heterogeneous Vehicles[J]. Journal of Systems & Management, 2016, 25(1): 129-138.
[4] 范厚明, 杨翔, 李荡, 等. 基于生鲜品多中心联合配送的半开放式车辆路径问题[J]. 计算机集成制造系统, 2019, 25(1): 256-266.
FAN Hou-ming, YANG Xiang, LI Dang, et al. Half-Open Multi-Depot Vehicle Routing Problem Based on Joint Distribution Mode of Fresh Food[J]. Computer Integrated Manufacturing Systems, 2019, 25(1): 256-266.
[5] LI Yan, LIM M K, TSENG M L. A Green Vehicle Routing Model Based on Modified Particle Swarm Optimization for Cold Chain Logistics[J]. Industrial Management & Data Systems, 2018, 119(3): 473-494.
[6] QIN Gao-yuan, TAO Feng-ming, LI Li-xia. A Vehicle Routing Optimization Problem for Cold Chain Logistics Considering Customer Satisfaction and Carbon Emissions[J]. International Journal of Environmental Research and Public Health, 2019, 16(4): 576-576.
[7] WANG Zi-qi, WEN Pei-han. Optimization of a Low-Carbon Two-Echelon Heterogeneous-Fleet Vehicle Routing for Cold Chain Logistics under Mixed Time Window[J]. Sustainability, 2020, 12(5): 1967.
[8] CAO Er-bao, LAI Ming-yong, YANG Hong-ming. Open Vehicle Routing Problem with Demand Uncertainty and Its Robust Strategies[J]. Expert Systems With Applications, 2014, 41(7): 3569-3575.
[9] MOGHADDAM B F, RUIZ R, SADJADI S J. Vehicle Routing Problem with Uncertain Demands: An Advanced Particle Swarm Algorithm[J]. Computers & Industrial Engineering, 2012, 62(1): 306-317.
[10] 管峰, 钟铭, 韦达. 需求不确定的车辆路径鲁棒优化模型[J]. 上海海事大学学报, 2015, 36(4): 27-30.
GUAN Feng, ZHONG Ming, WEI Da. Robust Optimization Model of Vehicle Routing with Demand Uncertainty[J]. Journal of Shanghai Maritime University, 2015, 36(4): 27-30.
[11] 邓烨, 朱万红, 唐建. 随机需求有时间窗的路径优化及补救策略研究[J]. 计算机工程与应用, 2018, 54(11): 241-248.
DENG Ye, ZHU Wan-hong, TANG Jian. Study on Vehicle Routing Problem with Stochastic Demands and Time Windows Combining with New Remediation Strategies[J]. Computer Engineering and Applications, 2018, 54(11): 241-248.
[12] 杨翔, 范厚明, 徐振林, 等. 模糊需求下多中心开放式车辆路径优化[J]. 计算机集成制造系统, 2019, 25(2): 469-479.
YANG Xiang, FAN Hou-ming, XU Zhen-lin, et al. Optimization of Open Multi-Depot Vehicle Routing Problem with Fuzzy Demand[J]. Computer Integrated Manufacturing Systems, 2019, 25(2): 469-479.
[13] HU C, LU J, LIU X, et al. Robust Vehicle Routing Problem with Hard Time Windows under Demand and Travel Time Uncertainty[J]. Computers and Operations Research, 2018, 94: 139-153.
[14] 赵家俊, 于宝琴. 现代物流配送管理[M]. 北京: 北京大学出版社, 2004: 49-52.
ZHAO Jia-jun, YU Bao-qin. Modern Logistics Delivery Management[M]. Beijing: Peking University Press, 2004: 49-52.
[15] 马向国, 刘同娟, 杨平哲, 等. 基于随机需求的冷链物流车辆路径优化模型[J]. 系统仿真学报, 2016, 28(8): 1824-1832.
MA Xiang-guo, LIU Tong-juan, YANG Ping-zhe, et al. Vehicle Routing Optimization Model of Cold Chain Logistics Based on Stochastic Demand[J]. Journal of System Simulation, 2016, 28(8): 1824-1832.
[16] 梁承姬, 邹倩倩. 带温度决策的冷链物流车辆路径优化研究[J]. 广西大学学报(自然科学版), 2017, 42(5): 1802-1809.
LIANG Cheng-ji, ZOU Qian-qian. Research on Vehicle Routing Problem with Temperature Variable in Cold Chain Logistics[J]. Journal of Guangxi University (Natural Science Edition), 2017, 42(5): 1802-1809.
[17] 张倩, 熊英, 何明珂, 等. 不确定需求生鲜电商配送路径规划多目标模型[J]. 系统仿真学报, 2019, 31(8): 1582-1590.
ZHANG Qian, XIONG Ying, HE Ming-ke, et al. Multi-Objective Model of Distribution Route Problem for Fresh Electricity Commerce under Uncertain Demand[J]. Journal of System Simulation, 2019, 31(8): 1582-1590.
[18] 吴丽荣, 胡祥培, 饶卫振. 考虑燃料消耗率的车辆路径问题模型与求解[J]. 系统工程学报, 2013, 28(6): 804-811.
WU Li-rong, HU Xiang-pei, RAO Wei-zhen. New Capacity-Vehicle-Routing-Problem Model and Algorithm for Reducing Fuel Consumption[J]. Journal of Systems Engineering, 2013, 28(6): 804-811.
[19] 刘宝碇, 赵瑞清. 随机规划与模糊规划[M]. 北京: 清华大学出版社, 1998: 79-82.
LIU Bao-ding, ZHAO Rui-qing. Stochastic Programming and Fuzzing Programming[M]. Beijing: Tsinghua University Press, 1998: 79-82.
[20] 郁磊, 史峰, 王辉, 等. MATLAB智能算法30个案例分析[M]. 2版. 北京: 北京航空航天大学出版社, 2015: 178-186.
YU Lei, SHI Feng, WANG Hui, et al. Analysis of 30 Cases of MATLAB Intelligent Algorithm[M]. Beijing: Beijing University of Aeronautics & Astronautics Press, 2015: 178-186.
[21] 辜勇, 袁源乙, 张列, 等. 带时间窗的多中心半开放式车辆路径问题[J]. 中国机械工程, 2020, 31(14): 1733-1740.
GU Yong, YUAN Yuan-yi, ZHANG Lie, et al. Multi-Depot Half Open Vehicle Routing Problem with Time Windows[J]. China Mechanical Engineering, 2020, 31(14): 1733-1740.
Routing Optimization of Semi-open Cold-chain Logistics Vehicle under Random Demand
LI Xiang, MIN De-quan, ZHANG Qi
(College of Transportation Engineering, Dalian Maritime University, Liaoning Dalian 116026, China)
The work aims to reduce the cost of cold-chain logistics distribution, while ensuring that customer experience and carbon emissions meet enterprise requirements. In the overall consideration of the transportation distance, customer soft time window constraints, carbon emissions, fresh deterioration and other factors, a multi-objective fresh distribution routing optimization model was established with the lowest total cost, including refrigeration cost and penalty cost for delivery time, the lowest carbon emissions and the highest freshness of fresh products as the objectives, and a simulated annealing algorithm was designed to verify the solution with a cold-chain logistics enterprise in Beijing as an example. The fresh product distribution scheme was obtained. According to the comparison of distribution modes, the multi-center semi-open distribution mode had more advantages in reducing cost and shortening routing length, in which the total transportation cost and the total distance traveled by vehicles were reduced by 8.41% and 36.36% respectively compared with single-center independent distribution mode. Under uncertain demand, reasonable decision-making routing can effectively reduce the distribution cost while meeting the freshness and carbon emission standards of fresh products.
cold-chain logistics; routing optimization; semi-open; uncertain demand; random programming; simulated annealing
TB485.3;U492.2+2
A
1001-3563(2022)07-0160-10
10.19554/j.cnki.1001-3563.2022.07.020
2021-08-23
国家社会科学基金(18VHQ005)
李想(1997—),男,大连海事大学硕士生,主攻物流系统优化与模拟仿真。
闵德权(1963—),男,博士,大连海事大学教授,主要研究方向为旅游管理、交通运输规划与管理。
责任编辑:曾钰婵

