基于Burgers模型对缓冲材料EPE压缩蠕变行为的分析

刘艳华，黄利强，付志强，何争辉，张武杰，刘昊喆

缓冲与隔振

基于Burgers模型对缓冲材料EPE压缩蠕变行为的分析

刘艳华a,b，黄利强a,b，付志强a,b，何争辉a,b，张武杰a,b，刘昊喆a,b

（天津科技大学 a.轻工科学与工程学院 b.包装创新设计实验室，天津 300222）

为解决缓冲材料发泡聚乙烯因蠕变引起保护失效的问题，基于Burgers模型，分析载荷、应力保持时间对EPE压缩蠕变行为的影响。根据不同应力下的不同保持时长压缩蠕变试验结果，拟合EPE不同应力下的压缩蠕变试验数据，分析不同应力、应力保持时间下的EPE蠕变过程中蠕变总量、弹性应变、黏弹性应变和黏性应变的变化规律。Burgers四元件力学模型对EPE不同应力下的压缩蠕变实验数据拟合度为0.992 4～0.998 9。在同一应力保持时间下，随着应力从3.3 kPa增加到5.3 kPa，弹性模量1、弹性模量2、黏度系数2、黏度系数1都逐渐减小，蠕变总量、黏性应变呈非线性显著增加，弹性应变、粘弹性应变呈线性微量增加；在同一应力下，随着应力保持时间从20 d增加到120 d，弹性应变一直保持不变，占蠕变总量的比例降低，粘弹性应变先微量增加后保持不变，占蠕变总量的比例降低，黏性应变增加，占蠕变总量的比例增加。Burgers模型可较准确地模拟EPE不稳定蠕变阶段和稳定蠕变阶段的压缩蠕变行为；应力的增加导致EPE抵抗变形的能力变弱，引起蠕变量增加；应力保持时间的增加对弹性应变无影响，对稳定蠕变阶段的黏弹性应变无影响，对黏性应变的增加有显著影响。

发泡聚乙烯；缓冲材料；Burgers模型；蠕变；压缩

发泡聚乙烯材料（EPE）是现代运输包装中常用的一种具有较高缓冲能力的新型环保包装材料，多用于包装电子、电器、精密仪器等产品[1]。产品在储存和运输过程中对缓冲材料会有一定程度的挤压，尤其产品在仓库中长期静压放置会产生蠕变，蠕变形变过大导致包装物、缓冲材料和产品间的孔隙变大，会极大降低缓冲材料的缓冲能力，加重冲击和振动对产品的破坏，因此，需要对缓冲材料EPE进行蠕变试验，试验结果对缓冲材料的设计具有指导意义。

当材料受到恒定的外力作用时，形变随时间变化的现象叫作蠕变。国内外许多学者已经对蠕变开展了研究，包括本构模型[2-5]、有限元模拟[6-7]，蠕变行为预测[8-9]等。乔卓等[10]对三峡库区黄土坡滑坡滑带土进行直剪蠕变试验，并采用指数型经验蠕变模型对蠕变曲线进行拟合，结果表明该模型能较好模拟黄土坡滑坡滑带土的蠕变特征。Soliman等[11]对不同碳纳米管含量的碳纳米管/环氧树脂复合材料的剪切蠕变试验进行了研究，并提出了2种改进的流变模型来模拟蠕变行为。王珂等[12]利用Ansys软件对管壳式换热器壳体进行高温蠕变分析，模拟结果与文献报道的一致。马永等[13]对橡胶材料构建本构模型，并通过Abaqus/UPYPER编译的子程序与有限元软件关联，仿真结果与实验结果吻合度较好。孙同生等[14]利用有限元方法预测储运发射箱堆码15年后底层发射箱的蠕变变形。Achereiner等[15]开发阶梯等温法对聚丙烯进行拉伸蠕变试验，并用于表征长达约100年的蠕变行为，证明此方法的合理性。

EPE是一种黏弹性材料，其蠕变行为比金属或岩石等材料的更明显，但是鲜有学者对其蠕变行为进行研究。Burgers模型是由Maxwell模型和Kelvin模型串联得到，能表现瞬时弹性、延迟弹性和黏性流，EPE蠕变形变由3部分组成：普弹形变、高弹形变和黏性流动，故选用四元件Burgers模型来描述EPE蠕变总量、弹性应变、黏弹性应变、黏性应变的变化规律，为EPE的蠕变行为的进一步研究奠定基础。

1 试验

1.1 材料与设备

主要材料：EPE由天津中天塑胶制品有限公司提供，密度为15 kg/m3，尺寸为100 mm×100 mm× 50 mm。

主要设备：DY-2冲击试验机（图1a），陕西科技大学；TP3加速度采集系统，Lansmont（美国）；LK-G400激光位移传感器，基恩士有限公司；蠕变测试仪（图1b）；ETH-408-40-CP-AR可程式恒温恒湿试验箱（图1c），巨贸仪器（北京）有限公司。

图1 试验设备

1.2 方法

1）确定载荷。参照GB/T 8167—2008《包装用缓冲材料动态压缩试验方法》[16]在常温下进行动态压缩试验，选择跌落高度为460、660、760、970 mm，重锤质量为0.434、0.868、1.15、2.15、3.29、5.93、7.93、9.93 kg，每组试验重复3次取平均值，得到最大冲击加速度-静应力曲线，参照杨杰等[17]提出的用对勾函数拟合动态冲击曲线较准的方法，拟合结果见图2，相关系数2均在0.92以上，估计最大冲击加速度的最低点对应的静应力具有合理性，静应力为2.26～5.58 kPa。根据实际蠕变测试仪的自重为33 N，故选择的蠕变应力为3.3、4.3、5.3 kPa。

2）预处理。将恒温恒湿箱内的温度分别调至21 ℃，并保持50%的相对湿度，试样和蠕变测试仪放置在试验环境下24 h。

3）试验步骤。参照GB/T 14745—2017《包装用缓冲材料蠕变特性试验方法》[18]进行，在21 ℃进行应力水平（3.3、4.3、5.3 kPa）的压缩蠕变试验120 d，每组试验重复3次取平均值，绘制应变-时间曲线（见图3）。分析应力保持时间对EPE的蠕变影响的计算点分别取20、40、60、80、100、120 d。运用Burgers模型，采用Origin Pro 2018C自定义非线性拟合函数对蠕变曲线进行拟合，自动拟合得到各参数值，计算不同应力、应力保持时间下的弹性应变、黏弹性应变和黏性应变。

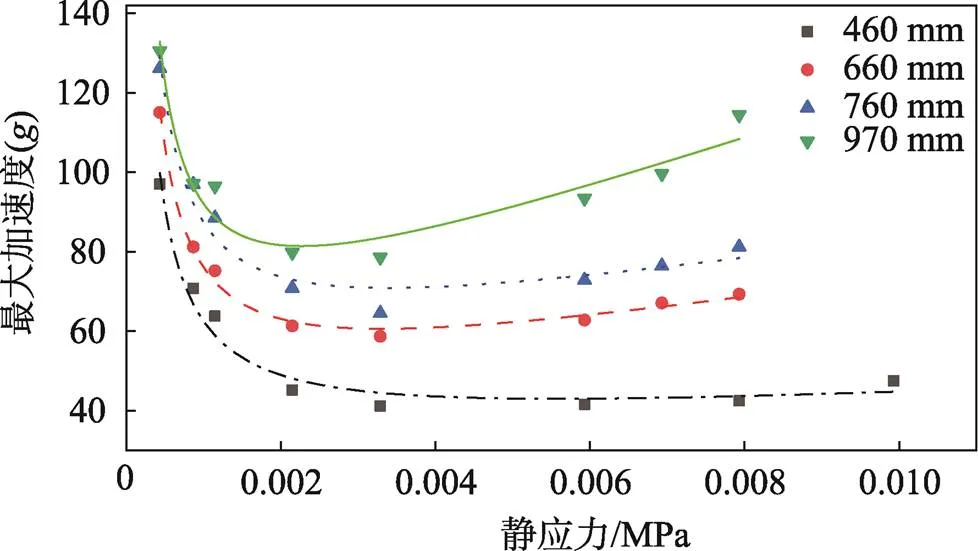
图2 动态压缩实验

图3 不同应力下的蠕变试验结果

Fig.3 Creep test results at different stresses

2 结果与分析

2.1 EPE蠕变行为的模拟

Burgers模型是4个元件组合而成的，其力学模型见图4，可描述EPE的形变：弹簧1受力后立即产生瞬时形变，卸载后可立即恢复形变，故可模拟普弹形变；弹簧2和粘壶2并联产生的形变随时间变化，卸载后形变会随时间的增加缓慢恢复，故可模拟高弹形变；粘壶3产生的形变随时间呈线性发展，卸载后形变不恢复，故可模拟黏性流动。材料[19]的压缩蠕变行为和Burgers模型拟合结果见图5，从图5中可以看出随着时间的延长，材料逐渐被压实，必然会出现蠕变速率趋于零的趋势，Burgers模型用来预测第3阶段的蠕变行为具有一定的误差，但可以较为准确地模拟不稳定蠕变阶段和稳定蠕变阶段的压缩蠕变行为。将这3部分元件串联起来，产生的总形变为3部分元件形变之和，在蠕变过程中，施加恒定应力为0，加载过程形变随时间的变化关系式为：

式中：0为恒定应力；为蠕变时间；()为蠕变过程中的总应变；1为蠕变过程中的弹性应变；2()为蠕变过程中的黏弹性应变；3()为蠕变过程中的黏性应变；1、2为普弹和高弹形变的弹性模量；1、2为黏性系数。

对式（1）进行求导可得Burgers模型的蠕变速率与时间的公式：

经过足够长时间后，材料的蠕变速率接近于恒定值：

各分量应变占蠕变总量的公式为：

在试验周期内3个应力水平下蠕变行为的应变-时间关系、蠕变速率-时间关系见图6—7，它们的蠕变行为大致相似，体现了前2个阶段的特征。在加载初期，EPE发生瞬时弹性形变，应力与应变成正比，与时间无关，随后产生黏弹性应变和黏性应变，蠕变速率随加载时间增加先减小后趋于稳定，蠕变曲线平稳上升。

图5 EPE压缩蠕变行为和Burgers模型拟合

图6 应变-时间曲线

图7 蠕变速率-时间曲线

基于式（1），应用Origin Pro 2018C自定义非线性拟合函数拟合EPE蠕变曲线数据点，自动拟合参数和相关系数2见表1，求出各拟合曲线与蠕变试验曲线相关系数2均在0.99以上，说明Burgers模型可以较为准确地模拟EPE不稳定蠕变阶段和稳定蠕变阶段的压缩蠕变行为。基于式（4）求出3个应力下各分量应变占比。

由表1可知，随着应力水平的增加，EPE的弹性模量1从59.33 kPa降低到45.73 kPa，说明EPE抵抗大载荷瞬时形变的能力变弱。弹性模量2从35.42 kPa降低到16.64 kPa，说明抵抗初始蠕变大载荷形变的能力变弱。由于EPE属于非线性弹性材料，故增大应力导致应变非线性增加，文用中弹性+黏弹性+黏性组合下的Burgers模型去描述材料蠕变性能，必然会出现弹性模量随着应力变化而变化的现象。黏度系数2从17 872.676 19 MPa·s降低到11 903.448 12 MPa·s，说明到达稳定蠕变阶段的时间在减小；黏度系数1从191 419.546 40 MPa·s降低到183 843.539 46 MPa·s，稳定阶段的蠕变速率从1.721 26×10−8增加到2.882 89×10−8，可知应力的增加会引起蠕变速率的增加。

2.2 不同应力下的EPE蠕变结果分析

相同的应力保持时间（20、40、60、80、100、120 d）时，不同的应力对蠕变的影响见图8。由图8a可知，在20 d的应力保持时间下，应力从3.3 kPa增加到5.3 kPa时，蠕变总量从0.175 4呈非线性增加到0.455 8，其中弹性应变从0.055 6呈线性增加到0.115 9，黏弹性应变从0.090 1呈非线性增加到0.290 1，黏性应变从0.029 7呈线性增加到0.049 8。弹性应变和黏性应变的增加相对不显著，黏弹性应变的增加相对显著，蠕变总量的增加主要依靠黏弹性应变的增加。由图7b—f可知，在40、60、80、100、120 d的应力保持时间的不同应力下也有相同的变化规律。应力变化对EPE的蠕变行为影响较大，在5.3 kPa应力水平下保持20 d产生的蠕变总量约为3.3 kPa下应力水平保持120 d产生蠕变总量的1.39倍。弹性应变、黏性应变、黏弹性应变、蠕变总量有着相同的变化规律，其中黏性应变随着保持时间的变化而变化，变化规律仍需进一步分析。

表1 Burgers模型在不同应力水平下的拟合参数

Tab.1 Simulated parameters of the Burgers model at different stress levels

图8 不同应力保持时间下各应变分量与应力关系

2.3 应变分量随着应力保持时间变化分析

相同的应力（3.3、4.3、5.3 kPa）时，不同的应力保持时间对蠕变的影响见图9。由图9a可知，随着应力保持时间的增加，3.3 kPa应力下的蠕变总量从0.175 4呈线性增加到0.327 3，弹性应变为常数，一直保持在0.055 6，说明应力保持时间对弹性应变无影响，黏弹性应变在20～60 d时从0.090 1增加到0.093 2，在60～120 d时保持0.093 2不变，依据式（1）可以推断出3.3 kPa应力下保持60 d时已经处于稳定蠕变阶段。黏性应变从0.029 7呈线性显著增加到0.178 5，蠕变总量的增加主要依靠黏性应变。由图8b—c可知，在4.3、5.3 kPa应力的不同保持时间下，也存在着弹性应变为常数，黏性应变呈线性显著增加，蠕变总量依靠黏性应变呈线性显著增加的规律，但黏弹性应变与在3.3 kPa应力条件下不同的是：在20 ～80 d略有增加，在80～120 d保持不变，说明在4.3、5.3 kPa应力下保持80 d时已经处于稳定蠕变阶段。

2.4 应变分量占蠕变总量的变化分析

相同的应力（3.3、4.3、5.3 kPa）时，不同的应力保持时间对各分量应变占蠕变总量比例的影响见图10。随着应力保持时间的增加，3.3 kPa应力下弹性应变占蠕变总量的比例从0.317 0降低到0.169 9，黏弹性应变占蠕变总量的比例从0.513 7降低到0.284 8，黏性应变占蠕变总量的比例从0.169 3增加到0.545 4。由图10b—c可知，在4.3、5.3 kPa应力的不同保持时间下，也存在着弹性应变、黏弹性应变占蠕变总量比例降低，黏性应变占蠕变总量比例增加的规律。在3.3 kPa的恒定应力、保持时间20～60 d时，黏弹性应变占蠕变总量的比例大于黏性应变的比例，60 d以后黏性应变占蠕变总量的比例大于黏弹性应变的比例，说明蠕变的主要体现从黏弹性应变转变为黏性应变。在4.3、5.3 kPa的恒定应力，保持时间20 ～ 120 d时，黏弹性应变占蠕变总量的比例一直大于黏性应变的比例，说明蠕变主要体现为黏弹性应变。

图9 3个应力下各分量应变与应力保持时间关系

图10 3个应力下各分量应变占比与应力保持时间关系

3 结语

实验数据与Burgers模型拟合相关系数2均在0.99以上，说明Burgers模型可准确模拟EPE不稳定蠕变阶段和稳定蠕变阶段的压缩蠕变行为。随着应力的增加，EPE抵抗大载荷形变的能力变弱、抵抗初始蠕变大载荷形变的能力变弱、到达稳定蠕变阶段的能力变快、引起稳定阶段的蠕变速率增加。在相同保持时间下，随着应力的增加，弹性应变和黏性应变的增加相对不显著，黏弹性应变的增加相对显著，蠕变总量的增加主要依靠黏弹性应变的增加。在相同应力下，随着保持时间的增加，弹性应变不受影响，其占蠕变总量的比例降低；黏弹性应变先增加后不变，其占蠕变总量的比例降低；黏性应变逐渐增加，其占蠕变总量的比例增加。

[1] 冯勇. EPE缓冲材料双向性能比较分析[J]. 中国包装工业, 2007(10): 47-48.

FENG Yong. Comparison and Analysis of Bidirectional Properties of EPE Cushioning Materials[J]. China Packaging Industry, 2007(10): 47-48.

[2] 杨武, 侍克斌, 何建新, 等. 不同膜厚复合土工膜的蠕变特性及模型研究[J]. 岩土工程学报, 2021, 43(5): 955-961.

YANG Wu, SHI Ke-bin, HE Jian-xin, et al. Creep Characteristics and Model Study of Composite Geomembrane with Different Film Thicknesses[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(5): 955-961.

[3] PING Cao, WEN You-dao, WANG Yi-xian, et al. Study on Nonlinear Damage Creep Constitutive Model for High-Stress Soft Rock[J]. Environmental Earth Sciences, 2016, 75(10): 1-8.

[4] 胡其志, 王芝超, 丁志刚. 基于分数阶导数的岩石蠕变本构模型研究[J]. 河南理工大学学报(自然科学版), 2021, 40(6): 163-168.

HU Qi-zhi, WANG Zhi-chao, DING Zhi-gang. Study on the Rock Creep Constitutive Model Based on Fractional Derivative[J]. Journal of Henan Polytechnic University (Natural Science), 2021, 40(6): 163-168.

[5] DEAN G. Modelling Non-Linear Creep Behaviour of an Epoxy Adhesive[J]. International Journal of Adhesion and Adhesives, 2006, 27(8): 636-646.

[6] 郭大猷, 黄小平, 王芳. 有机玻璃观察窗的蠕变特性及数值模拟[J]. 上海交通大学学报, 2019, 53(5): 513-520.

GUO Da-you, HUANG Xiao-ping, WANG Fang. The Creep Properties and Numerical Simulation for PMMA Window[J]. Journal of Shanghai Jiao Tong University, 2019, 53(5): 513-520.

[7] 江明, 王世梅, 李高, 等. 基于滑坡土体渗流与蠕变耦合模型的ABAQUS二次开发[J]. 水电能源科学, 2020, 38(6): 124-127.

JIANG Ming, WANG Shi-mei, LI Gao, et al. Secondary Development of ABAQUS Based on Creep-Seepage Coupling Model of Landslide Soil[J]. Water Resources and Power, 2020, 38(6): 124-127.

[8] YANG J L, ZHANG Z, SCHLARB A K, et al. On the Characterization of Tensile Creep Resistance of Polyamide 66 Nanocomposites. Part Ⅱ: Modeling and Prediction of Long-term Performance[J]. Polymer, 2006, 47: 6745-6758.

[9] YANG T C, WU T L, HUNG K C, et al. Mechanical Properties and Extended Creep Behavior of Bamboo Fiber Reinforced Recycled Poly(Lactic Acid) Composites Using the Time-Temperature Superposition Principle[J]. Construction and Building Materials, 2015, 93: 558-563.

[10] 乔卓, 崔德山, 陈琼, 等. 三峡库区黄土坡滑坡滑带土卸荷状态下的直剪蠕变特性研究[J]. 安全与环境工程, 2021, 28(4): 156-163.

QIAO Zhuo, CUI De-shan, CHEN Qiong, et al. Direct Shear Creep Behavior of Sliding Zone Soil under Unloading Stress on Huangtupo Landslide in the Three Gorges Reservior Area[J]. Safety and Environmental Engineering, 2021, 28(4): 156-163.

[11] SOLIMAN E, KANDIL U F, TAHA R M. Limiting Shear Creep of Epoxy Adhesive at the FRP-Concrete Interface Using Multi-Walled Carbon Nanotubes[J]. International Journal of Adhesion and Adhesives, 2012, 33: 36-44.

[12] 王珂, 刘遵超, 刘彤, 等. 管壳式换热器壳体的高温蠕变有限元分析[J]. 机械工程材料, 2014, 38(4): 87-90.

WANG Ke, LIU Zun-chao, LIU Tong, et al. Finite Element Analysis of High Temperature Creep of Shell for Shell and Tube Heat Exchanger[J]. Materials for Mechanical Engineering, 2014, 38(4): 87-90.

[13] 马永, 赵世平, 卢丙举, 等. 橡胶减震器材料时变蠕变力学行为研究[J]. 舰船科学技术, 2021, 43(1): 95-101.

MA Yong, ZHAO Shi-ping, LU Bing-ju, et al. Research on Time-Depending Creep Mechanical Behavior of Rubber Shock Absorber Material[J]. Ship Science and Technology, 2021, 43(1): 95-101.

[14] 孙同生, 于存贵, 秦予铮, 等. 多管火箭武器储运发射箱长期储存蠕变性能预测[J]. 国防科技大学学报, 2020, 42(5): 60-67.

SUN Tong-sheng, YU Cun-gui, QIN Yu-zheng, et al. Prediction of Creep Performance for Multiple Launch Rocket Canister under Long-Term Storage[J]. Journal of National University of Defense Technology, 2020, 42(5): 60-67.

[15] ACHEREINER F, ENGELSING K, BASTIAN M, et al. Accelerated Creep Testing of Polymers Using the Stepped Isothermal Method[J]. Polymer Testing, 2013, 32(3): 447-454.

[16] GB/T 8167—2008, 包装用缓冲材料动态压缩试验方法[S].

GB/T 8167—2008, Testing Method of Dynamic Compression for Packaging Cushioning Materials[S].

[17] 杨杰, 付志强, 张蕾, 等. EPE动态冲击曲线拟合函数对比[J]. 包装工程, 2021, 42(9): 32-36.

YANG Jie, FU Zhi-qiang, ZHANG Lei, et al. Comparison of EPE Dynamic Impact Curve Fitting Function[J]. Packaging Engineering, 2021, 42(9): 32-36.

[18] GB/T 14745—2017, 包装用缓冲材料蠕变特性试验方法[S].

GB/T 14745—2017, Test Method of Creep Properties for Package Cushion Material[S].

[19] 杨岁桥, 王宁宁, 张虎. 高温冻土的蠕变特性试验及蠕变模型研究[J]. 冰川冻土, 2020, 42(3): 834-842.

YANG Sui-qiao, WANG Ning-ning, ZHANG Hu. Study on Creep Test and Creep Model of Warm Frozen Soil[J]. Journal of Glaciology and Geocryology, 2020, 42(3): 834-842.

Compressive Creep Behavior of EPE Cushioning Material Based on Burgers Model

LIU Yan-huaa,b, HUANG Li-qianga,b, FU Zhi-qianga,b, HE Zheng-huia,b, ZHANG Wu-jiea,b, LIU Hao-zhea,b

(a.School of Light Industry Science and Engineering b. Laboratory for Innovative Design of Package, Tianjin University of Science & Technology, Tianjin 300222, China)

In order to solve the problem of protection failure caused by creep of cushioning material foamed polyethylene, the effects of load and stress holding time on the compressive creep behavior of EPE cushioning material were analyzed based on Burgers model. Based on the results of the compression creep test results of different holding time under different stresses, the compression creep test data of EPE under different stresses were fitted to analyze the changes of creep total, elastic strain, viscoelastic strain and viscous strain during the creep process of EPE under different stresses and stress holding time. The experimental data fit of Burgers four-element mechanical model for compression creep of EPE under different stresses ranged from 0.992 4 to 0.998 9. At the same stress holding time, as the stress increased from 3.3 kPa to 5.3 kPa, the elastic modulus1, elastic modulus2, viscosity coefficient2and viscosity coefficient1all decrease. The total creep and viscous strain increase nonlinearly, while the elastic strain and viscoelastic strain increase linearly. At the same stress, as the stress retention time increases from 20 days to 120 days, the elastic strain remains constant and its proportion to the total creep decreases. The viscoelastic strain increases slightly at first and then remains constant, and its proportion to the total creep decreases while the viscous strain increases and its proportion to the total creep increases. Burgers model can accurately simulate the compressive creep behavior of EPE in unstable creep stage and stable creep stage. The increase of stress leads to the weakening of EPE's ability to resist deformation and the increase of creep. The increase of stress holding time has no effect on the elastic strain, and has no effect on the viscoelastic strain in the stable creep stage, but has a significant effect on the increase of viscous strain.

foamed polyethylene; cushioning material; Burgers model; creep; compressive

TB484.3

A

1001-3563(2022)07-0146-08

10.19554/j.cnki.1001-3563.2022.07.018

2021-08-17

天津市教委科研计划（自然科学）（2019KJ209）

刘艳华（1996—），女，天津科技大学硕士生，主攻包装动力学。

付志强（1982—），男，博士，天津科技大学讲师，主要研究方向为运输包装数值模拟技术。

责任编辑：曾钰婵