位移约束下火箭橇结构拓扑优化方法研究

王磊 李泽商 顾凯旋 戚晓玲

摘要：兼顾安全性与经济性的高性能结构优化设计是结构设计领域的重要需求，面向火箭橇结构的拓扑优化设计对火箭橇试验具有重要意义。本文在火箭橇结构动力学仿真分析的基础上，基于变密度法建立了火箭橇结构的拓扑优化模型，利用伴随矢量求解了目标函数与约束函数关于设计变量的灵敏度，通过移动渐近线算法驱动了设计变量的更新迭代，最后对拓扑优化设计的结果进行了校验。结果表明，提出的位移约束下的火箭橇结构拓扑优化设计方法在经济性与安全性方面对火箭橇结构的设计是有效的，拓展了火箭橇结构的设计思路。

关键词：火箭橇；动力学分析；变密度法；结构设计；拓扑优化

中图分类号：TH122文献标识码：ADOI：10.19452/j.issn1007-5453.2022.02.015

火箭橇是指采用火箭發动机作为动力，推动载有试验件的火箭沿专门建造的高精度轨道高速滑行的地面设备，可以较好地解决各类飞行器在研制过程中有关高速度及高加速可能带来的诸多技术问题[1-3]，为军队提供强大的体系化空中力量，是国防军队现代化的重要体现[4]。

火箭橇与轨道的动态性能直接影响到车载试验件的试验环境，将直接决定动态跑车试验结果的准确性和可靠性[5-6]。国内外一些学者对高速火箭橇系统动力学方面开展了研究，Gerasimov等[7]对橇轨之间的橇-轨接触变形及运动稳定性进行了分析；Laird等[8]对高速火箭橇橇-轨撞击过程进行了仿真分析；王健等[9]对火箭橇轨道不平顺功率谱密度进行了分析；顾凯旋等[10]提出了基于梁单元等效的全时段火箭橇动力学分析方法。

随着航空零部件研制工作的日新月异，其设计思路也在不断拓宽和自由化[11]，拓扑优化技术可用于结构概念设计阶段，以获得具有更合理材料分布的启发式设计[12]，这已成为高性能工程结构设计领域最活跃课题之一。结构拓扑优化常用方法主要有变密度法（SIMP）[13-14]、水平集法（LSM）[15]和渐进优化法（ESO）[16]等。尽管历经30多年的研究发展，结构拓扑优化技术已经逐渐被众多工程领域所重视，但大部分研究成果只停留在学术层面，少数较为成熟的应用在构件级、简单工况的层面[17]。在整体复杂结构层面，在火箭橇车体设计中运用拓扑优化技术的研究还比较缺乏。

为满足高性能火箭橇复杂车体设计的要求，本文拟建立位移约束下火箭橇结构的拓扑优化模型，并且对拓扑优化设计结果进行校验。首先，在火箭橇动力学仿真分析的基础上，建立基于SIMP法的火箭橇结构拓扑优化模型；其次，基于移动渐近线法（MMA）求解位移约束下的火箭橇结构的拓扑优化问题；最后，对拓扑优化设计结果建立含细节的火箭橇动力学分析的有限元模型，对设计结果进行安全性校验[18]。

1火箭橇动力学仿真分析

高精度轨道在加工、安装、使用过程中造成的几何不平顺是引起火箭橇与轨道结构振动的重要因素。本节将介绍考虑静态几何不平顺引起的附加接触力火箭橇结构动力学仿真方法。

3数值算例

考虑橇车结构的服役环境，橇车结构需要与试验件、滑块等相连接，因此需要建立非设计单元。单轨三滑块火箭橇模型的设计域及非设计域如图2所示，其中设计域为蓝色单元，非设计域为紫色单元。

有限元模型弹性模量为206GPa，泊松比为0.3。拓扑优化经过185次迭代终止，整个拓扑优化过程花费15min，最终获得的拓扑构型如图3所示，在保证位移滑块处不超过0.5mm的条件下实现减重超过60%。

拓扑优化过程中目标函数的变化曲线如图4所示。约束函数随迭代过程的变化曲线如图5所示。针对拓扑优化的结果，建立基于梁单元等效的含滑块细节的有限元模型如图6所示。其中，同一种颜色代表同一种属性。

梁单元的信息见表1，其中截面面积1代表梁两端截面面积中较大的一个，截面面积2代表两端截面面积较小的一个，由于火箭橇结构尾端需要与推进装备连接，因此建立偏置梁单元模型。

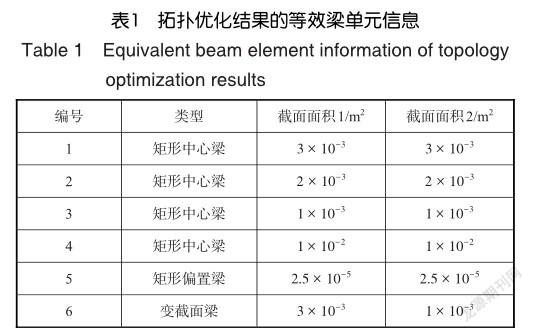
基于第1节介绍的火箭橇动力学仿真分析方法对根据火箭橇拓扑优化设计结果建立的等效梁单元模型进行动力学校验，得到滑块处的动力学响应曲线，如图7～图9所示，本文仅给出了其中一个滑块的结果，其余两个滑块的响应趋势和响应量级基本相同，三个滑块处的最大均方根加速度和最大应力见表2。

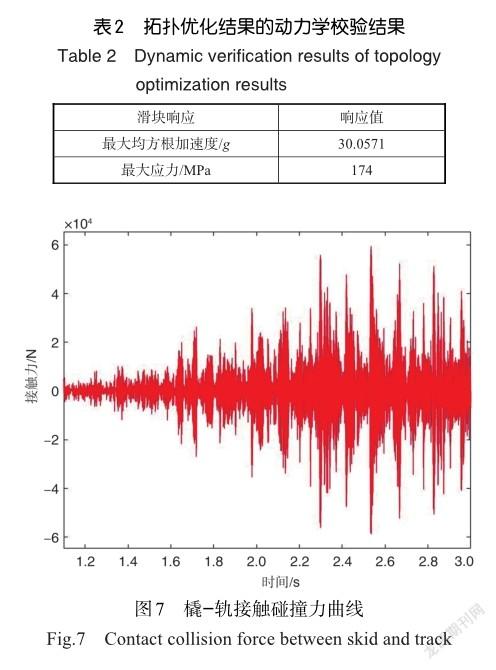
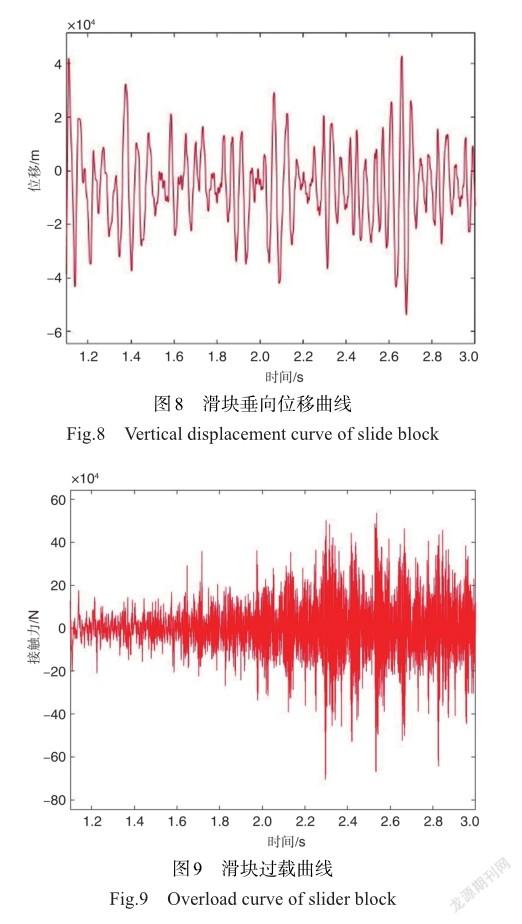
由于滑车速度不断加快，单位时间内滑块所经历的轨道不平顺变化不断增大，使得滑块与轨道的碰撞接触力增大，因此滑块的过载不断增加。观察校验结果发现，滑块处的位移变化不超过0.5mm，说明拓扑优化的有效性。

4结论

本文基于SIMP法建立了位移约束下高速火箭橇结构的拓扑优化模型，采用MMA法驱动拓扑优化模型中设计变量的更新迭代。针对拓扑优化的设计结果，建立了含滑块细节的火箭橇有限元模型，对设计结果进行了动力学仿真校验。结果表明，本文提出的位移约束下的高速火箭橇拓扑优化设计方法在满足位移约束条件的同时实现了超过60%的减重，兼顾了经济性与安全性。

参考文献

[1]王云.火箭橇试验滑轨的发展与展望[J].航空科学技术，2010，21（1）： 30-32. Wang Yun. Status and prospect for rocket sled track development in China[J]. Aeronautical Science & Technology， 2010，21（1）： 30-32. （in Chinese）

[2]郑严，史新兴.弹用涡轮喷气发动机火箭橇试验研究[J].推进技术，2001， 22（1）： 26-29. Zheng Yan， Shi Xinxing. Investigation of rocket sled test for missile turbojet engine[J]. Journal of Propulsion Technology， 2001， 22（1）： 26-29. （in Chinese）

[3]张翔宇，甘晓松，高波，等.固体火箭发动机火箭橇过载模拟试验方法[J].固体火箭技术，2016（6） ：751-754. Zhang Xiangyu， Gan Xiaosong， Gao Bo， et al. Rocket sled acceleration experiment method of SRM[J]. Journal of Solid Rocket Technology， 2016（6）： 751-754. （in Chinese）

[4]宋慶国.百年未有之大变局下的航空科技发展[J].航空科学技术，2021，32（3）：1-5. Song Qingguo. The development of aviation science and technology under changes unseen in a century[J].Aeronautical Science & Technology，2021，32（3）：1-5.（in Chinese）

[5]张立乾，邓宗才，郭富民，等.滑橇高速运动动态效应与滑轨平顺度的关系研究[J].弹道学报，2011， 23（2）：106-110. Zhang Liqian， Deng Zongcai， Guo Fumin， et al. Study on relation of slide-rail regularity and high-speed movement dynamic response of sled[J]. Journal of Ballistics， 2011， 23（2）： 106-110. （in Chinese）

[6]刘洪，姚冉中.研究火箭橇滑轨共振特性[J].电子测试，2018（13）：60-62. Liu Hong， Yao Ranzhong.Study on the response characteristics of the rocket skid rail[J]. Electronic Test， 2018（13）： 60-62. （in Chinese）

[7]Gerasimov S I，Erofeev V I，Kamchathyi V G，et al. The sliding contact condition in stability analysis of stage motion for a rocket sled track facility[J]. Journal of Machinery Manufacture and Reliability，2018，47（3）：221-226.

[8]Laird D J，Palazotto A N. Effect of temperature on the process of hypervelocity gouging[J]. AIAA Journal，2003，41（11）：2251-2260.

[9]王健，吴军基，陶钢.火箭橇轨道不平顺功率谱密度分析[J].弹道学报，2008， 20（4）： 81-80. Wang Jian， Wu Junji， Tao Gang. Analysis on power spectrum density of rocket sled rail irregularity[J]. Journal of Ballistics， 2008， 20（4）： 81-83. （in Chinese）

[10]顾凯旋，龚明生，王磊，等.双轨火箭橇全时程动力学仿真分析研究[J].航空工程进展，2020，11（2）： 245-250. Gu Kaixuan， Gong Mingsheng， Wang Lei， et al. Study on full timedynamicssimulationoftwo-trackrocketsled[J]. Advances in Aeronautical Science and Engineering， 2020， 11（2）： 245-250. （in Chinese）

[11]周梅萍，王中兴，赵云，等.航空领域增材制造技术专利态势分析[J].航空科学技术，2020，31（1）：44-51. Zhou Meiping，Wang Zhouxing，Zhao Yun，et al. Analysis on patent situation of additive manufacturing technology in aeronautic field[J].Aeronautical Science & Technology，2020，31（1）：44-51. （in Chinese）

[12]閻军，张晨光，霍思旭，等.宽弦风扇叶片空腔结构多目标轻量化设计[J].航空科学技术，2021，32（4）：60-64. Yan Jun，Zhang Chenguang，Huo Sixu，et al. Multi-objective lightweight design of the cavity structure of wide-chord fan blades[J]. Aeronautical Science & Technology，2021，32（4）：60-64. （in Chinese）

[13]Liu K，Tovar A. An efficient 3D topology optimization code writteninMatlab[J].StructuralandMultidisciplinary Optimization，2014，50（6）：1175-1196.

[14]Sigmund O. A 99 line topology optimization code written in Matlab[J]. Structural and Multidisciplinary Optimization，2001（21）：120-127.

[15]Wang Y，Wang X M，Guo D M. A level set method for structural topology optimization[J]. Computer Methods in Applied Mechanics and Engineering，2003，192：227-246.

[16]Radman A. Combination of BESO and harmony search for topology optimization of microstructures for materials[J]. Applied Mathematical Modelling，2021，90（2）：650-661.

[17]冯建春，来希雪.民用飞机典型连接结构优化设计探索[J].产业与科技论坛， 2021， 20（16）： 35-36. Feng Jianchun， Lai Xixue. Exploration on optimization design of civil aircraft typical connecting structures[J]. Industrial & Science Tribune， 2021， 20（16）： 35-36. （in Chinese）

[18]王德铎，张艳平，闫军，等.多体结构瑞利阻尼系数的确定[J].机械设计与制造，2010（1）： 230-231. Wang Deduo， Zhang Yanping， Yan Jun， et al. Calculation for the Rayleigh damping coefficient of multi-body structures[J]. Machinery Design & Manufacture， 2010（1）： 230-231. （in Chinese）

Research on Topology Optimization Method of Rocket Sled Track Structure Under Displacement Constraint

Wang Lei1，2，Li Zeshang1，Gu Kaixuan3，Qi Xiaoling3

1. Beihang University，Beijing 100191，China

2. Ningbo Institute of Technology，Beihang University，Ningbo 315100，China

3. Aviation Key Laboratory of Science and Technology on Life-support Technology，Xiangyang 441003，China

Abstract： The optimization design of high-performance structure considering both safety and economy is an important demand in the field of structural design. Topology optimization design for rocket sled track structure is of great significance for rocket skid test. Based on the dynamic simulation analysis of rocket sled track structure， the topology optimization model of rocket sled track structure is established based on SIMP method. The sensitivity of objective function and constraint function with respect to design variables is solved by using adjoint vector， and the update iteration of design variables is driven by MMA algorithm. Finally， the result of topology optimization is verified. The results show that the topology optimization design method of rocket sled track structure under displacement constraint is effective in economy and safety， and expands the idea of rocket sled track structure design.

Key Words： rocket sled track； dynamic analysis； SIMP method； structure design； topology optimization

Received： 2021-08-08；Revised： 2021-10-15；Accepted： 2021-11-19 Foundation item：Aeronautical Science Foundation of China（20182951014）