复合材料层合结构热压罐固化过程的多物理场-热流固解耦数值求解
李顶河 郭永刚 孟宪明
摘要:在复合材料层合结构热压罐固化成形过程中,温度场和固化度场的均匀性对残余应力和变形具有重要影响。对于厚度较大的复合材料层合结构,流动压实的影响不可忽略,同时热压罐空气热流场和模具温度场也会对复合材料结构内部的温度场产生较大影响。本文同时考虑固化动力学模型、热传导模型、残余应力模型、流动压实模型、热压罐热流场以及模具温度场,建立了复合材料热压罐热流固多物理场解耦求解模型;在多个时变参数影响下,分析了大厚度复合材料层合结构热压罐固化成形过程中残余应力、固化度场、温度场以及纤维体积分数的变化规律。
关键词:复合材料;多场耦合;热压罐;固化;模具
中图分类号:TB332文献标识码:ADOI:10.19452/j.issn1007-5453.2022.02.006
碳纤维增强复合材料由于其优异的力学性能和较低的密度,在各种轻量化的应用中有较大的需求量,尤其是在航空航天和汽车行业[1-2]。在热压罐固化成形过程中,由于纤维和树脂的热不匹配、复合材料结构与模具的热不匹配、热压罐模具温度场的不均匀等影响,使得复合材料在热压罐成形脱模后会发生翘曲和回弹变形。由于传统的试错方法费时费力,有限元方法的发展为预测复合材料固化变形和残余应力、优化工艺参数提供了更有效的手段。
近年来,许多学者对热压罐复合材料固化过程进行了研究,Bogetti等[3]采用二维有限元方法模拟了任意截面形状和边界条件层合板的固化过程。Hu等[4]研究发现大厚度复合材料构件在固化成形过程中会出现温度不均匀分布现象。刘桂铭等[5]研究表明,固化过程中的过热现象会使得复合材料层合板的力学性能下降。
对于流动压实模型的研究,Loos等[6]和Springer[7]将整个固化过程中复合材料构件的压实假设成逐层进行。Gutowski等[8]将有效应力原理应用于复合材料的流动压实过程。张纪奎等[9]基于有限元软件建立了三维压实模型。乔炎亮等[10]研究了流动压实模型和黏弹性残余应力耦合模型,发现厚度增大、纤维体积分数梯度增大,残余应力的不均匀性也变大。Li等[11]和Xie[12]采用挤压海绵模型建立了帽形加筋板三维模型,通过设置芯模预制孔提高了树脂的流动均匀性。
现有残余应力模型大都不考虑流动压实模型,忽略纤维体积分数不均匀分布对于复合材料残余应力的影响,由早期的线弹性模型发展到现在的黏弹性模型。White等[13]采用积分型黏弹性模型对复合材料固化残余应力进行了研究。Zobeiry等[14-15]提出了伪黏弹性模型,并提出了一种微分形式的黏弹性模型表示方法,还指出微分形式与积分形式的黏弹性模型是等效的。Ding等[16]推导了考虑热弹性刚度因子的热流变复杂材料黏弹性本构模型。乔巍等[17]基于有限元软件ABAQUS比较了线弹性、路径依赖,以及黏弹性三种本构模型,表明黏弹性本构的预测效果更好。
热压罐的模具温度分布对于复合材料的成形质量具有重要影响。对于空气热流场和模具温度场的求解,许多学者进行了研究。张铖[18]基于CFX对复合材料的框架式模具温度场进行了精确化模拟。林家冠[19]通过在通风口处添加模拟风扇来减小模具温度场的不均匀性。Hu等[20]提出一种热补偿方法,通过安装导热翅片有效降低了模具表面的最大温差。Dolkun等[21]综合考虑温度均匀性和升温速率,利用回归模型来优化模具放置参数。
对于大厚度复合材料热压罐成形问题,固化热化学模型、流动压实模型、残余应力模型以及考虑热压罐热流场和模具温度场的多物理场耦合模型研究相对较少,多数只考虑了其中几个模型的耦合或采取顺序耦合来求解。由于模具型面温度的不均匀分布,会导致复合材料构件产生较大的温度梯度,进而影响复合材料的变形。本文将分析模具温度场的不均匀性对大厚度复合材料固化过程中的影响,对上述模块进行解耦求解,分析多物理场强耦合下的固化过程,这对于试验和生产具有一定的指导意义。
1固化过程的解耦数值求解理论框架
考虑复合材料固化过程中的热传导模型、固化动力学模型、多孔介质流动压实模型、复合材料黏弹性残余应力模型、热压罐热流场以及模具温度场,并采用解耦方式求解,如图1所示。在解耦模型中,首先求解热压罐模具温度场,然后将每一时间步的热压罐型面温度场作为热载荷施加到复合材料构件下表面,且假设复合材料构件上表面温度均匀。解耦模型考虑了复合材料的热传导与固化动力学模型、热传导与流动压实模型,以及空气热流场与模具温度场的双向耦合关系,残余应力模型与其他三个固化模型以及模具温度场与热传导模型的单向耦合关系,并直接求解上述理論模型。
1.1热-化耦合模型
在复合材料结构固化过程中,由于材料热传导系数比较小,热量在传递过程中出现温度迟滞现象。另外,对于大厚度大曲率复合材料构件来说,容易在厚截面复杂结构的位置产生较大温差和压力差,导致树脂流动不均,使得复合材料内部的温度场和固化度场产生较大梯度。本文考虑了树脂渗流对热传导模型的影响[11],采用傅里叶热传导定律来计算复合材料多孔介质结构内部的温度场。







由式(24)可以得到热压罐流场为湍流流动,采用k -ε模型能够较为精确地模拟模具温度场。
2模型验证
2.1复合材料黏弹性模型验证
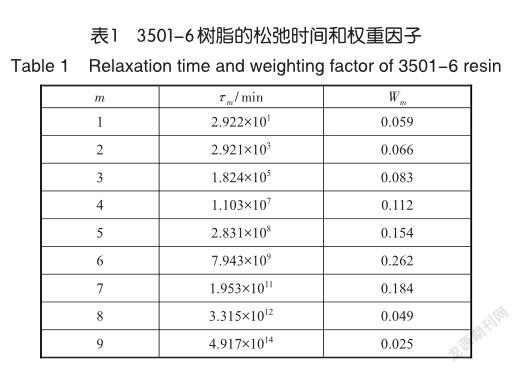
采用White等[13]建立的黏弹性残余应力模型,建立[0/90]s三维树脂基复合材料层合板模型,为了简化计算,采用1/8模型进行计算,复合材料层合板的尺寸为10.16cm×10.16cm×2.54cm,并采用AS4/3501-6复合材料的相关物性参数,模型的边界条件如图3所示。
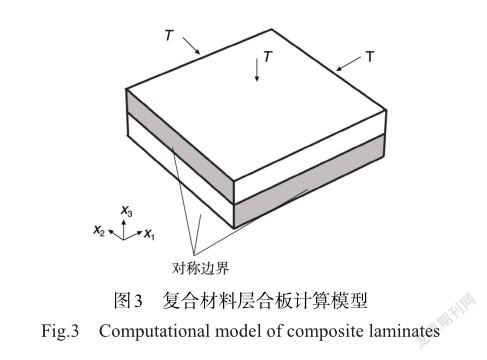
0°铺层内中心点的横向应力曲线如图4所示,本文计算的固化结束后的残余应力大小为32.2MPa,与White等[13]计算的32MPa基本吻合,证明了所建立广义Maxwell黏弹性残余应力模型的正确性。

2.2模具温度场模型验证分析
采用标准的k -ε湍流模型模拟模具温度场,计算结果与参考文献[19]的试验数据进行比较。热压罐内框架式模具如图5所示。边界条件为入口速度2.5m/s,出口压力为罐内压力(6atm, 1atm=101.325kPa),温度制度和模具以及空气的热物理参数参考文献[19]。为了衡量模具型面温度场的不均匀分布,将型面的最大温差作为标准,计算出的模具型面最大温差结果如图6所示,型面最大温差的最大值出现在升温结束阶段,最大值为20.98K。图7为模拟结果与参考文献[19]试验数据对比图,型面监测点E和F的最大误差不超过2.74%,且靠近入口端的型面温度预测精度要高于靠近出口端的型面温度,可以认为该流固共轭传热模型能够较为真实地模拟模具温度场。

3复合材料热流固解耦模型分析
3.1模具与层合板解耦传热模型
为了分析热压罐模具温度场对固化过程的影响,同时为了简化计算模型,提高计算效率,考虑如图8所示的解耦模型来计算复合材料层合板的多物理场耦合问题,将计算得到的模具温度场作为热载荷添加到大厚度复合材料层合板下表面,上表面的温度场假设为均匀,不考虑透气毡、脱模布等辅助材料的传热影响,假设四周热绝缘。本文假设复合材料层合板可以在模具表面滑动,不考虑型面变形对复合材料层合板的影响。
复合材料多孔介质流-热流固耦合模型考虑了流动压实模型(顶面吸胶)对温度场、固化残余应力和变形的影响,热压罐工艺温度采用AS4/3501-6树脂基复合材料的标准两保温温度制度,热压罐压力为0.689MPa,入口速度为2.5m/s,复合材料单向层合板的厚度为40mm。
保温阶段50min和60min的型面温度如图9所示,在升温结束后,随着保温时间的增加,型面温度场的梯度不断减小。
两保温温度制度构件底面的最大温差曲线如图10所示,最大温差在升温阶段随着温度的升高而增大,在保温过程中最大温差减小,在降温阶段最大温差又迅速增大,通过增加保温时间将有效减小温度场的不均匀分布。
模型中心点处的温度和纤维体积分数如图11所示,初始纤维体积分数为40.4%,随着温度的逐渐升高,树脂从纤维骨架中迅速被挤出,最终在120min时达到50.78%。

中间面中心纵向线的5个均布点的温度曲线如图12所示。在升温阶段,靠近入口端点的温度要高于同一时刻的靠近出口端点的温度,在46min时,1点与5点温差达到最大为6.9K;在降温阶段,靠近出口端点的温度逐渐大于靠近入口端点的温度,在固化结束后,5点与1点的最大温差达到最大为9.2K。
复合材料层合板1~5点的固化度如图13所示,受到模具温度场的影响,迎风侧的温度较高,树脂的固化交联反应更加剧烈,固化度率先达到凝胶点0.3,并提前完成固化。在第二保温阶段131min时,1点与5点的固化度差值最大,达到0.063。



固化完成后纖维体积分数沿厚度方向的分布曲线如图14所示,底面中心和顶面中心之间的纤维体积分数产生了非线性分布,底面中心的纤维体积分数为0.503,顶面中心的纤维体积分数为0.531。
3.2不同风速下的热流固耦合模型
为了分析热压罐罐内风速对于复合材料层合板固化过程的影响,建立不同风速工况下的单向复合材料层合板算例进行分析。分别计算了热压罐风速为2.5m/s、5m/s、7m/s和10m/s的热流固耦合算例,并分析风速大小对模具型面最大温差、复合材料层合板的固化度以及残余应力的影响。
如图15所示,在升温阶段风速为2.5m/s时最大温差为21.8K,风速为5m/s、7m/s、10m/s时的最大温差分别为18K、16.76K、13.67K。随着热压罐风速的增大,有效提高了空气热流与模具的对流换热效率,模具型面最大温差在逐渐减小。


图16给出了不同风速下中心点处的固化度曲线。随着风速的增大,固化提前越早,5m/s和10m/s的固化程度在 125min时的差值最大为0.044,此时的固化速率接近峰值。
受到风速大小的影响,复合材料单向层合板300min时的中心残余应力沿厚度方向的曲线分布如图17所示。残余应力的最大值在上表面中心,风速为2.5m/s时的上表面残余应力为3.305MPa,风速为10m/s时的上表面残余应力为1.1MPa,残余应力减小了约66.7%。这是由于随着热压罐风速的增大,模具的温度场不均匀性减小,从而导致复合材料层合板的残余应力减小。

3.3不同厚度的复合材料热流固耦合模型
为了分析厚度对于复合材料温度场和残余应力的影响,分别建立了30mm、35mm、45mm和50mm的复合材料层合板模型。图18给出了第二升温阶段层合板中心的温度历史,30mm板的中心点的温度最高,50mm的中心点的温度最低。由于复合材料层合板的厚度越大,内部的温度传导越慢,并产生较大的温度梯度和更大固化迟滞效应,所以30mm的层合板中心处的固化也会早于厚度更大的层合板。随着层合板厚度的增大,其中心点残余应力也在逐渐减小,如图19所示,这也可以进一步表明厚度较小的板会产生较大的变形。

4结论
本文建立了复合材料层合结构热压罐固化成形的多物理场-热流固解耦计算模型,同时考虑了黏弹性残余应力模型、热流场以及模具温度场模型,并与参考文献计算数据和试验结果进行了对比,验证本文所建立模型的正确性。由分析可知:复合材料顺风侧的温度要比背风侧的温度高,顺风侧的固化程度比背风侧高,随着风速的增大,模具型面的不均匀性减小,复合材料中心点的固化过程加快,沿厚度方向分布的残余应力将减小;随着复合材料一定范围内的厚度增大,复合材料的中心点温度以及沿厚度方向分布的残余应力都有所减小。
參考文献
[1]李航航,阎勇,尹航.战斗机新结构应用与新材料需求分析[J].航空科学技术, 2020, 31(4): 8-13. Li Hanghang, Yan Yong, Yin Hang. New structure application and new material requirement analysis for fighter aircraft[J]. Aeronautical Science & Technology, 2020, 31(4): 8-13. (in Chinese)
[2]程健男,徐福泉,张体磊.树脂基复合材料在直升机的应用及其制造技术[J].航空科学技术, 2021, 32(1): 109-114. Cheng Jiannan, Xu Fuquan, Zhang Tilei. Application and manufacturing technology of composites in helicopter[J]. Aeronautical Science & Technology, 2021, 32(1): 109-114. (in Chinese)
[3]Bogetti T A,Gillespie J W. Two-dimensional cure simulation of thick thermosetting composites[J]. Journal of Composite Materials,1991,25(3):239-273.
[4]Hu H,Cao D,Pavier M,et al. Investigation of non-uniform gelation effects on residual stresses of thick laminates based on tailed FBG sensor[J]. Composite Structures,2018,202:1361-1372.
[5]刘桂铭,湛利华,陈效平,等.厚截面复合材料固化温度不均匀性对力学性能的影响[J].玻璃钢/复合材料, 2018(9): 23-29. Liu Guiming, Zhan Lihua, Chen Xiaoping, et al. Effects of thickcompositecuringtemperaturenon-uniformityon mechanicalproperties[J].FRP/CM,2018(9):23-29.(in Chinese)
[6]Loos A C,Springer G S. Curing of epoxy matrix composites[J]. Journal of Composite Materials,1983,17(2):135-169.
[7]Springer G S. Resin flow during the cure of fiber reinforced composites[J]. Journal of Composite Materials,1982,16(5):400-410.
[8]Gutowski T G,Morigaki T,Cai Z. The consolidation of laminate composites[J]. Journal of Composite Materials,1987,21(2):172-188.
[9]张纪奎,张江,马志阳,等.厚截面层合板非同步固化的三维有限元分析[J].北京航空航天大学学报, 2013, 39(11): 1464-1469. Zhang Jikui, Zhang Jiang, Ma Zhiyang, et al. Threedimensional finite element analysis for non-synchronized cure of thick composite laminates[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(11): 1464-1469. (in Chinese)
[10]乔炎亮,张江涛,张梅,等.厚复合材料单向板流动-压实与残余应力耦合分析[C]//中国力学大会-2017暨庆祝中国力学学会成立60周年大会, 2017. Qiao Yanliang, Zhang Jiangtao, Zhang Mei, et al. Coupling analysis of flow-compaction and residual stress of thick composite unidirectional plate[C]//Chinese Mechanics Conference:2017 and Celebrating the 60th Anniversary of the Founding of the Chinese Society of Mechanics, Beijing, 2017.
[11]LiS,ZhanL,Chang T.Numericalsimulationand experimental studies of mandrel effect on flow-compaction behavior of CFRP hat-shaped structure during curing process[J]. Archives of Civil and Mechanical Engineering,2018,18(4):1386-1400.
[12]Xie P,Zhu S,Shao Y,et al. Simulation and experimental analysis of autoclave co-curing CFRP hat-stiffened panels with silicone airbag mandrels[J]. Iranian Polymer Journal,2019,28(6):505-514.
[13]White S R,Kim Y K. Process-induced residual stress analysis of AS4/3501-6 composite material[J]. Mechanics of Composite Materials and Structures an International Journal,1998,5(2):153-186.
[14]ZobeiryN,VaziriR,PoursartipA.Differential implementation of the viscoelastic response of a curing thermoset matrix for composites processing[J]. Journal of Engineering Materials & Technology,2006,128(1):90-95.
[15]Zobeiry N,Vaziri R,Poursartip A. Computationally efficient pseudo-viscoelastic models for evaluation of residual stresses in thermoset polymer composites during cure[J]. Composites Part A:Applied Science and Manufacturing,2010,41(2):247-256.
[16]Ding A,Li S,Wang J,et al. A three-dimensional thermoviscoelastic analysis of process-induced residual stress in composite laminates[J]. Composite Structures,2015,129:60-69.
[17]喬巍,姚卫星,马铭泽.复合材料残余应力和固化变形数值模拟及本构模型评价[J].材料导报, 2019, 33(24): 4193-4198. Qiao Wei, Yao Weixing, Ma Mingze. Numerical simulation and constitutive models evaluation of residual stresses and processinduced deformations of composite structures[J]. Materials Reports, 2019, 33(24): 4193-4198. (in Chinese)
[18]张铖.大型复合材料结构热压罐工艺温度场权衡设计[D].哈尔滨:哈尔滨工业大学, 2009. Zhang Cheng. Curing temperature field trade-off design method of large-scale composite material structure in autoclave process[D]. Harbin: Harbin Institute of Technology, 2009. (in Chinese)
[19]林家冠.復合材料构件热压罐固化的温度场分析与调控[D].大连:大连理工大学, 2015. Lin Jiaguan. Curing temperature field analysis and regulation of composite components in autoclave process[D]. Dalian: Dalian University of Technology, 2015. (in Chinese)
[20]Hu J,Zhan L,Yang X,et al. Temperature optimization of mold for autoclave process of large composite manufacturing[J]. Journal of Physics,2020,1549(3):032086.
[21]Dolkun D,Wang H,Wang H,et al. Influence of large framed mold placement in autoclave on heating performance[J]. Applied Composite Materials,2020,27(6):811-837.
[22]Dave R. A unified approach to modeling resin flow during composite processing[J]. Journal of Composite Materials,1990,24(1):22-41.
[23]Shin D D,Hahn H T. Compaction of thick composites:simulation and experiment[J]. Polymer Composites,2004,25(1):49-59.
Numerical Solution of Multiphysics-Thermo-Fluid-Solid Decoupling for the Curing Process of Composite Laminated Structure Autoclave
Li Dinghe1,Guo Yonggang1,Meng Xianming2
1. Civil Aviation University of China,Tianjin 300300,China
2. China Automotive Technology Research Center Co.,Ltd.,Tianjin 300399,China
Abstract: The uniformity of the temperature field and the curing degree field during the curing and molding process of the composite material laminated structure has an important influence on the residual stress and deformation. For the composite material laminated structure with a larger thickness, the influence of flow compaction cannot be ignored, and at the same time the air heat flow field and mold temperature field of the autoclave will also have a greater impact on the temperature field inside the composite structure. This paper also considers the curing kinetics model, the heat conduction model, the residual stress model, the flow compaction model, and the autoclave heat flow field and mold temperature field, and a decoupling solution model of thermo-fluid-solid multiphysics for composite material autoclave is established. Under the influence of several time-varying parameters, the change law of residual stress, curing degree field, temperature field and fiber volume fraction during the curing process of large-thickness composite laminated structure in autoclave is analyzed.
Key Words: composite; multi-field coupling; autoclave; curing; mold
Received: 2021-10-19;Revised: 2021-11-17;Accepted: 2021-12-18
Foundation item: General Program of National Natural Science Foundation of China(12072364)

