大地测量坐标系转换的MATLAB教学软件平台开发
高春春,吕子豪,张 朋,韩卓阳,李 丽
(南阳师范学院 地理科学与旅游学院,河南 南阳 473061)
0 引言
大地测量学是测绘类专业一门重要的专业基础课程,在测绘高等人才培养和学科建设中发挥着重要的作用[1].该课程基础理论性强,公式推导复杂,大多数学生学习起来较为困难.其中,不同测量坐标系之间的相互转换是大地测量学实践和教学的基础问题[2],在传统教学实践过程中,因其涉及复杂的计算过程,往往导致大多数学生难以有效熟练掌握[3].
软件平台可以有效帮助学生在短时间内熟练掌握复杂的计算原理和方法[4-5],本文基于MATLAB软件强大的数据处理功能,编写了不同测量坐标系之间的相互转换程序,并设计和开发了相应的可视化软件操作平台.该平台可以实现单点、批量数据的坐标转换计算任务,能够帮助学生加深理解大地测量坐标系转换的复杂概念,提升学生学习兴趣,提高大地测量学的教学质量.该平台所含的坐标系转化程序还可应用于测绘领域的实践与科研工作中.
1 理论和方法
1.1 大地坐标与空间直角坐标相互转换
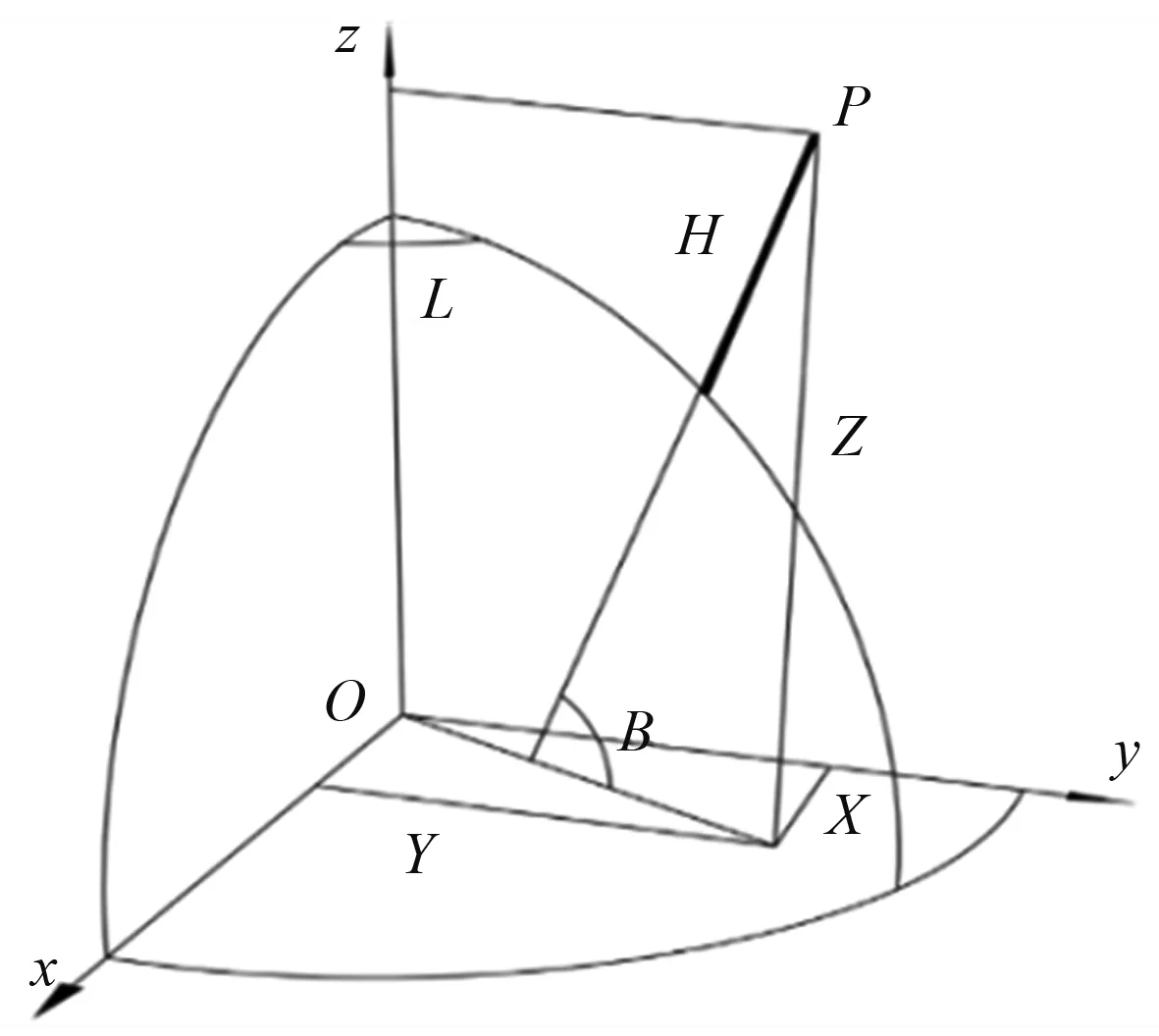
图1 大地坐标(B, L, H)与空间直角坐标(X, Y, Z)示意图
如图1所示,地球空间中任意一点P所在大地坐标为大地纬度B、大地经度L和大地高H,所在空间直角坐标为(X,Y,Z),两者的相互转换公式为[6]:
(1)
(2)
其中,N为卯酉圈曲率半径,e为第一偏心率,a,b分别为参考椭球长半轴、短半轴.在公式(2)中需使用迭代法求解大地纬度B值,初次迭代B值设为0.
1.2 高斯平面坐标正反算
高斯投影坐标正反算是将大地坐标(B,L)与高斯投影的平面坐标(x,y)进行互相转换,其正算公式为[6]:
(3)
其中,t=tanB,η2=e′2cos2B,当l=0时,X为从赤道起算的子午线弧长.其计算公式的一般形式:
(4)
其中系数:
(5)
而反算公式为[6]:
(6)
当y=0时,l=0,B=Bf,其中Bf为底点纬度.Bf的计算公式为:
(7)
其中
f1=c(β2cosBf+β4cos3Bf+β6cos5Bf+β8cos7Bf)
(8)
f1中含有待定量Bf,因此需要进行迭代计算,初次迭代时可令f1=0.
2 程序设计与实现
2.1 MATLAB子程序
为了实现上述坐标系之间的相互转换,本文共编写8个MATLAB子函数(见表1)来进行计算.其中,defval函数[7]用来设置函数变量的默认值, deg2dms和dms2deg函数用来实现角度不同格式之间的相互转换, ellipsoidpara函数用来计算不同椭球的参数以及辅助函数, arc_length函数用来计算子午圈和平行圈的弧长,coordtransfer函数用来实现大地坐标与空间直角坐标的相互转换,gauss_bl2xy和gauss_xy2bl函数分别实现高斯平面坐标的正反算.

表1 MATLAB计算函数
2.2 可视化教学软件平台
为了提供更加友好的软件交互界面,方便用户操作和理解,本文基于MATLAB的GUIDE(Graphic User Interface Development Environment)开发了大地测量坐标系转换的软件操作平台.图2展示了大地测量坐标系转换软件的教学平台起始界面,通过下拉选项可以选择不同的椭球、角度格式、高斯投影带宽以及计算目的.同时,该教学平台还可以帮助学生实现单点和批量数据的计算(见图3和图4).
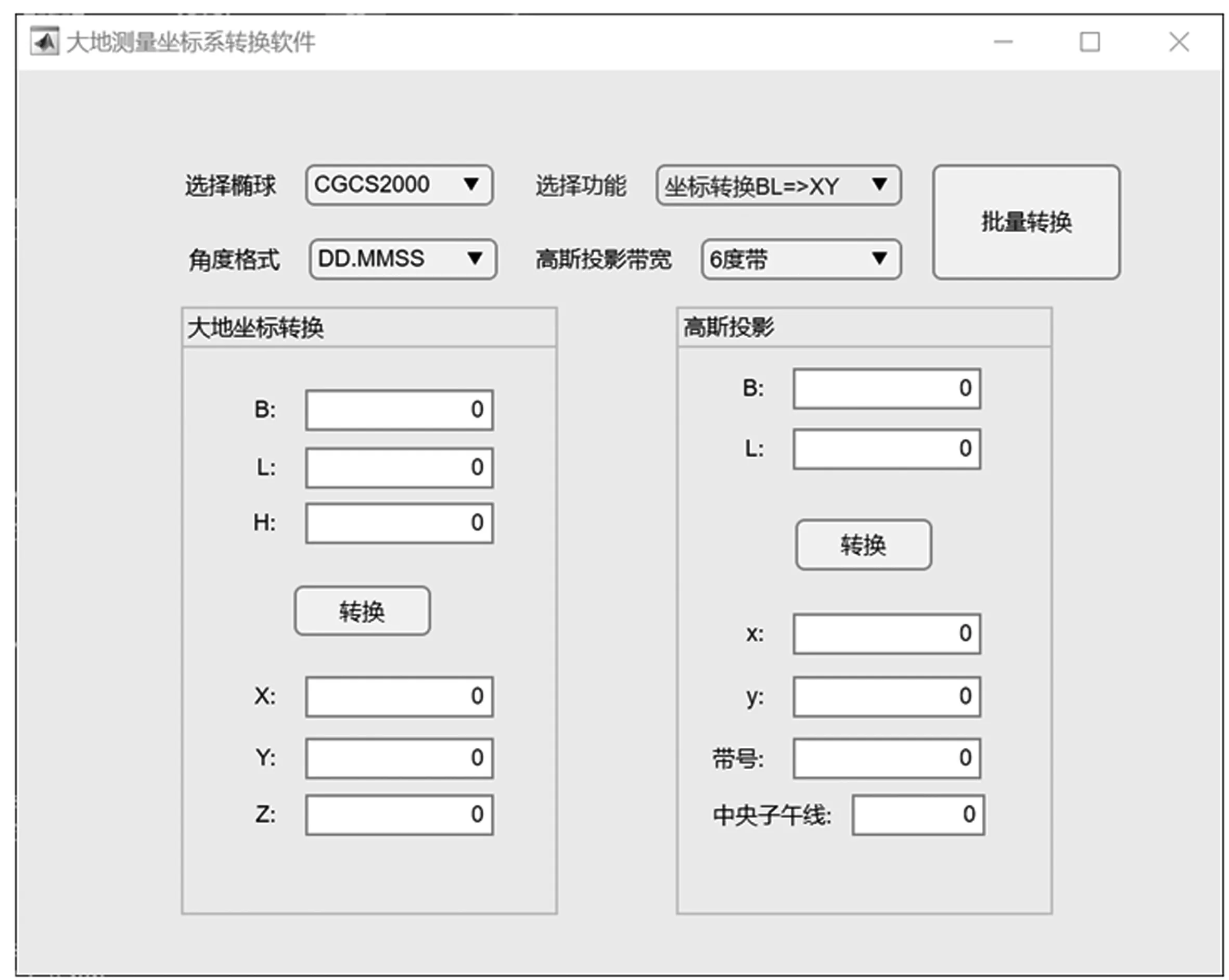
图2 大地测量坐标系转换教学软件平台
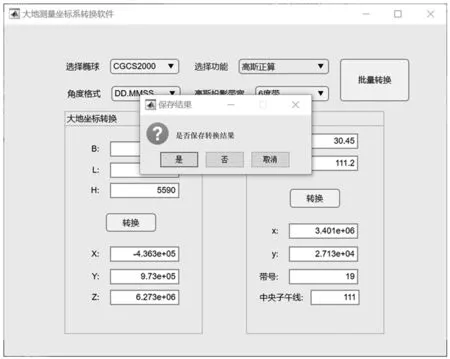
图3 单点计算
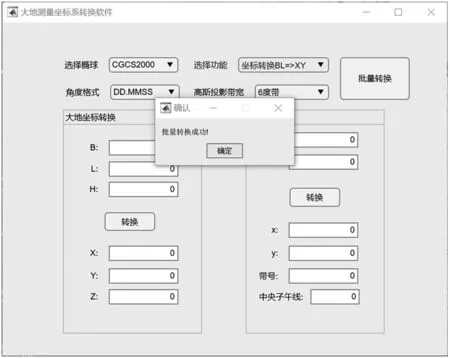
图4 批量计算
3 模拟计算与精度分析
为了验证软件的计算效果,本文随机生成了50000组大地坐标数据(B,L,H),进行计算.首先,将50000组大地坐标转换为空间直角坐标和高斯平面坐标,随后再利用软件将空间直角坐标和高斯平面坐标反算回大地坐标,反算后的大地坐标与原始大地坐标之间差值的均方根可以作为软件内符合精度的评价指标.表2展示了原始和反算大地坐标之间差值的均方根,在大地坐标与空间直角坐标的转换中,该软件大地纬度的内符合精度可达到10-8秒,大地经度的精度达到10-10秒,大地高的精度达0.005毫米;在大地坐标与高斯平面坐标的转换中,大地纬度的内符合精度达到10-6秒,大地经度的内符合精度达10-5秒,上述精度可以满足常规的大地测量学教学和实践需求.

表2 坐标转换误差
4 结论
本文通过MATLAB 软件实现了大地测量坐标系中大地坐标、空间直角坐标和高斯平面坐标相互转换的程序设计和可视化编程,借助 MATLAB软件强大的数值计算能力和丰富的可视化表达,建立了相关坐标系转换的基本算法和可视化教学软件平台.模拟计算和精度分析结果显示,该程序运算速度快,计算精度高,结果可靠性强.此教学软件平台不仅可作为大地测量学本科和研究生教学的辅助软件,以提升学生实践能力和学习兴趣,平台所包含的程序还可应用于测绘领域的实践与科研工作中.

