浅层地温场连续监测和高精度模拟时空误差研究

张利伟，刘 春，李济琛，寇玉冬

南京大学 地球科学与工程学院，南京 210023

浅层地温能具备埋藏深度较浅，就近开发利用，分布广泛等诸多优势，是未来一种重要的清洁可再生资源，中国正在大规模开发利用并逐渐实现产业化（王宝军等，2009；舟丹，2018；鄂建，2019；罗楷，2019）。目前多个城市也在开展相关的地温能开发工作（鄂建等，2015；景佳俊等，2018；张甫仁等，2018；王春晖等，2019），而地温场是描述地温能分布的重要内容。

一般地下温度主要通过钻孔温度获知，根据某地区的钻孔测温资料，可以对该区的地温进行综合性的评价。李英杰等（2015）通过土壤温度速测仪测温探头研究了关中地区6 m深度范围内天气变化对于温度的影响。DTS（分布式光纤温度传感器,Distributed fibre optic temperature sensor简称）在测温方面具有高时空分辨率以及其连续性测量的可靠性，是测量钻孔温度的一种重要方法（Tobias et al., 2009; Tyler et al., 2009）。Brabyn等（2014）等利用iButton评估了遥感卫星获得的南极洲干谷地区的地表温度，两者具有较好的耦合性。姜洪涛等（2013）等利用PT100温度传感器探究了不同覆盖层土体对地表温度的影响，发现混凝土等硬质地面对应的土体温度明显高于裸土和草地等类型土体温度。除此之外，城市热岛、气候条件、水文地质条件以及地质构造等因素也对地温的分布产生一定的影响（卫万顺等，2010；Liu et al., 2011;刘丹丹等，2014；李英杰等，2015；Kurylyk et al.，2015）。

温度的变化与时间和空间有关，通过建立适当的地温热传导模型可以对不同深度的地温进行很好地描述。采用不同的初始或边界条件，许多基于一维热传导方程建立的模型被用来研究竖向的地层温度分布。Menberg等（2014）分别将两个连续的恒定值作为上边界条件对一维热传导方程进行求解，并假设在此期间地表的温度保持相对稳定。Kurylyk 等（2014）等通过指数形式的初始和边界条件得到了热传导方程解析解，探究了气候变化对于地下水的影响，并验证了其相对于线性初始和边界条件的准确性。Marielle等（2010）等通过蒙特卡洛方法对年均温度边界增加了10000种高斯噪音，预测了未来1000年的地温变化。吴志伟等（2010）利用特定的热物理参数将解析解与通过FEMLAB得到的有限差分数值解进行比较，证明了解析解的可行性。根据模拟得到的结果，结合相关的条件，可以探究影响地温场分布特征的因素。目前针对地温演化规律方面的分析展开了大量的研究，通常采用不同的函数形式描述地表温度的变化，且预测温度多是月或年平均温度。

由于现场高精度地层结构和低温数据的获取和监测较为困难，在开展地温分布计算和预测时，通常在建模中采用特定的或平均的地层参数，以及采用日或月平均温度作为边界条件，其空间和时间精度等影响因素还不确定。本文采用DTS、iButton等多种仪器对南京市多个地温监测钻孔进行连续的高精度监测，得到不同时刻随深度变化的温度数据。基于精细的地层参数测量数据和高精度的地表连续测温数据，以一维地温热传导模型为基础，模拟了特定时间内的温度变化规律；探究了不同空间精度和时间精度的地温变化特征，及其模拟精度误差；并利用该模型进行预测，进一步分析了地温变化的季节特征。

1 野外测温

1.1 研究区概况

南京市位于长江中下游，三面环山，一面濒水，主城区位于长江东南，区内地形地貌复杂，以丘陵、低山为主，还有河流堆积形成的三级阶地，长江冲淤积作用形成的河漫滩。且岩土体类别多样，自上元古界到新生界均有分布，控制性断裂主要有北向西走向的南京—湖熟断裂，近东西走向幕府山—焦山断裂，近东西走向的定淮门—琵琶湖断裂。四季分明，属北热带季风气候区，年平均气温为15.7℃，年平均降水量为1077.71 mm。选取南京地区布设的3个钻孔，如图1所示，深度为80～100 m，分别位于南京市六合区玉带镇通江集村和龙袍镇以及江宁区汤山镇四维村，并依次记为Z1、Z2、Z3，该测区地下水位为2～5 m，且钻孔内水位与外界相通，表1为三个钻孔的地层岩性，同时获取了3钻孔分层的热扩散系数以及含水率、密度等热物理参数。

表1 钻孔地层岩性Table 1 Lithology of boreholes

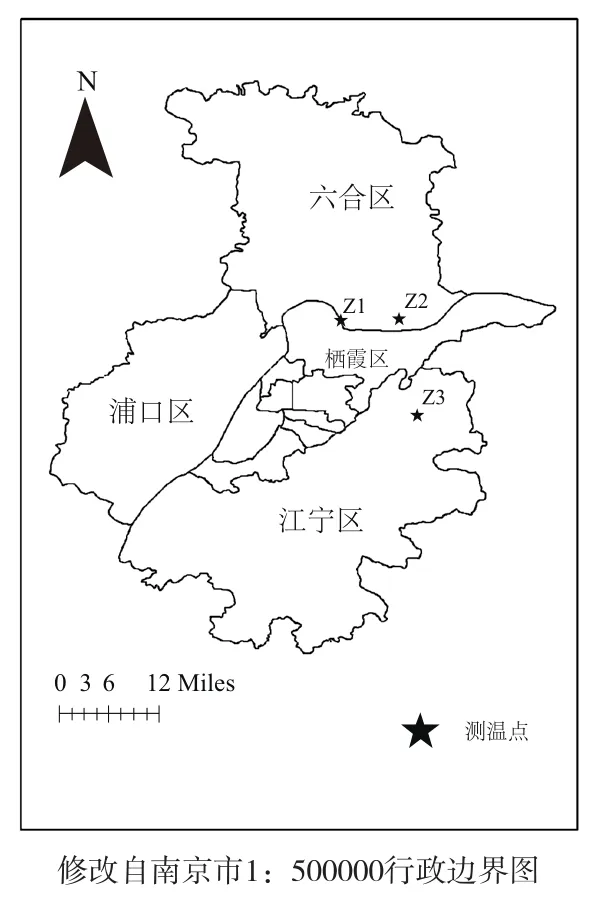
图1 研究区测温点位图Fig. 1 Temperature measurement points in the study area

1.2 测温传感器及设备

为了获得钻孔中温度场高精度的时空分布数据，采用分布式光纤温度传感器（Distributed fibre optic temperature sensor，DTS）、PT100 和 iButton 温度传感器进行测温，表2为各仪器简介。DTS可以一次性获得连续随深度变化的温但由于系统损耗和噪音影响（Tyler et al., 2009），DTS所测精度相对较低；而PT100的测温精度较高，但只能测单点的温度值。因此，为获得钻孔内较高精度的连续地温，采用精度较高的PT100来校正减少DTS的测温误差。同时，iButton可以连续测量一段时间内的地温变化，并且可以设置测温的时间间隔。因此，本次野外地温监测综合采用了DTS，PT100以及iButton三种传感器，以获得连续的地温数据。

表2 不同类型温度传感器Tabel 2 Different types of temperature sensors

1.3 现场测温方案和数据处理

测温通常会在每季度进行一次， DTS和PT100测温同步进行，而iButton只需将其埋入地表即可。如图2所示为野外测温简图，将光纤一端下放到钻孔中，另一端连接光纤解调仪，DTS每隔30 s测一次温度。另外，通过下放PT100探头到钻孔中不同位置，0～2 m每隔0.5 m对PT100进行深度标记，2～20 m处对PT100每隔1m进行深度标记，待显示屏温度稳定时，根据标记深度读取此处温度数据。iButton进行参数设置后，套上薄塑料袋埋入地表。由于地温在短时间内变化不大，为了使测量结果更加精确，选取1～2 h内DTS所测地温的平均值作为该时刻的温度。测温结束后，用PT100的温度数据对DTS数据进行对比校正，即可获得准确的地温数据。对于浅层地温分布，通常自上到下依次为变温层、恒温层以及增温层，如图3为三钻孔不同季度地温变化曲线，由图示可知地表以下20 m左右地温随深度变化基本不大，可视为恒温层，因此本次研究区域在地表以下20 m。而20 m以后为增温层，该处地温主要受岩石性质以及大气热流的影响，温度随深度大致呈线性变化，一般为3℃/100 m，但是Z3钻孔地温梯度较大，达到6℃/100 m，这是由于该处恰好处于汤山—仑山复背斜，核部具有断裂构造，为地表水的入渗以及深部循环提供了通道，促进了热量的向下运移（栾光忠等，1998）。

图2 野外监测示意简图Fig. 2 Schematic diagram of field instruments

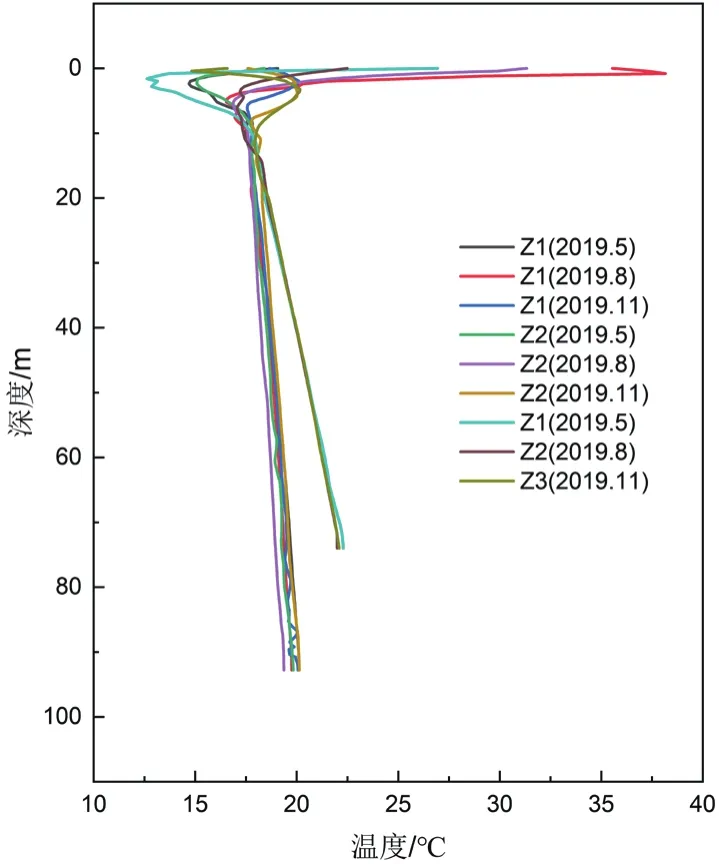
图3 三钻孔温度—深度变化曲线Fig. 3 Temperature-depth curves of three drillings

2 热传导模型

2.1 模型的建立

浅部土壤地层变化较为复杂，较浅部几乎（约0～10 m）无地下水流动，而较深部（10～20 m）地下水流速较小，尤其对于短期模拟影响较小。为简化计算，做出如下假设：（1）各土层为均匀介质，且各向同性（2）不考虑地下水的流动。在浅地表以热传导为主的传热模型中，通常采用如下形式的一维热传导方程（吴志伟等，2010；Kurylyk et al.,2014）：

α为热扩散系数，单位是m2/s，λ是水土耦合热传导系数，单位是J·s-1m-1k-1，u是在深度为z处，t时刻的温度，ρw是流体的密度，单位是kg·m-3，cwρw和cρ分别代表流体和岩石-流体基质的体积比热容，单位是J·m-3k-1。

代入初始以及边界条件，就可以得到任意时间段的模拟地温，以上过程通过Matlab求解计算。

2.2 边界条件和参数确定

提取从2019年7月中旬到2019年11月初共106 d的地温数据，并分别用DTS测出三个钻孔第一天某时段和最后一天对应该时段温度数据，前者作为初始温度，后者与模拟后的结果进行对比验证。iButton在0 m处所测随时间变化的温度作为上边界条件，地表温度主要受太阳辐射以及空气温度等影响（Kurylyk et al.，2015），如图4所示，三条曲线分别代表Z1、Z2、Z3在模拟时间内所测地表温度。以恒温层温度作为下边界条件，此处温度为18±0.5℃。取深度步长Δx=0.4 m，对应DTS最小空间分辨率，时间步长Δt=2 h，即iButton在0 m处每隔两小时所测温度值。分别取不同深度的土体测定其热传导系数、比热容以及密度等，如表3、4所示，利用计算得到的热扩散系数算术平均值作为模拟参数。

表3 不同钻孔平均热容量参数Table 3 Averaged thermal capacity of boreholes

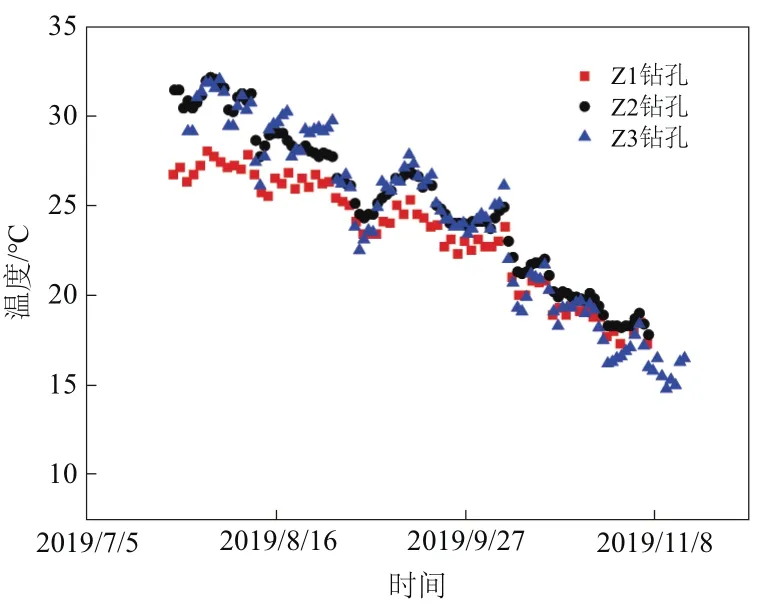
图4 地表温度变化示意图Fig. 4 Surface temperatures of three boreholes

表4 不同土样的热扩散系数Table 4 Thermal diffusivity of materials

在Δx和Δt不变的前提下，当探究空间精度影响时，需分层设置热物理参数，探究时间精度影响时，分别以地表日均温度和月均温度作为边界条件。

3 结果与分析

3.1 模拟结果和误差分析

图5为模拟结果的变化情况，图6为106天时实测地温和模拟地温对比曲线图，可以看到，实测值Tm与模拟值Ts随深度变化曲线趋势大致相同，除浅层0～7 m处实际值与模拟值差异较大，其余深度吻合性均较好，误差基本处于±0.2℃范围内。

模拟时间内，在0～7 m处，Z1、Z2孔Ts偏大，Z3孔偏差较小，这是由于地表覆盖物的影响（姜洪涛等，2013），Z1、Z2孔处地表为草地，会对太阳的辐射起阻挡作用，而Z3孔地表几乎为裸土，对地表传热影响相对较小。相对于Z1和Z2孔，Z3孔在浅地表0～7 m处模拟结果较好，考虑到 Z3孔在该研究深度内几乎全为泥岩，物质组成相对较为单一，受各向异性的影响较小。Z1、Z2以及Z3孔在7～20 m处Tm略高于Ts，这是由于地下水的下渗透能够加速热流的传递 （邓孝等，1989；吴志伟等，2010；Kurylyk et al., 2014）。此外，由于没有考虑到实际地层的不均匀性，以及在测量过程中数据的波动等，使得模拟结果与实测值之间存在误差（Tyler et al., 2009；Lesperance et al., 2010; Kurylyk et al., 2015）。

综合图5和图6可以看出，在模拟时间内，浅层地表0～7 m处越接近地表温度变化幅度越大，而对于7～20 m地层，地温随时间变化幅度较小，总体温度变化在1～2℃内，并且最终稳定在18℃左右，说明在短时间内较深处地温变化不大。图5中红色箭头表示随着时间的推移，热量逐渐向更深处地层扩散，同等时间内Z3孔地表温度影响深度较大，这是由于传热速率不同，Z3孔2～20 m处为泥岩，热扩散率较大，地层传热速率较快。

图5 模拟时间内温度随深度变化云图（从左至右依次为钻孔Z1、Z2、Z3）Fig. 5 Temperature-depth cloud map in simulation time (From left to right, drilling Z1、Z2 and Z3)

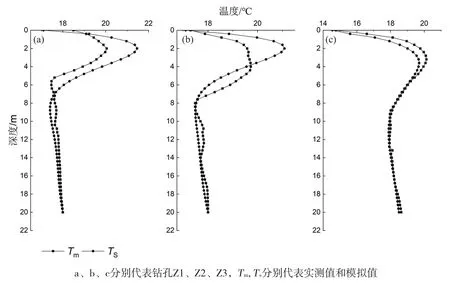
图6 模拟值与实测值对比图Fig. 6 Comparison between measured and simulated groundwater temperature versus depth

综上所述，温度向下传递的过程中需要一定的时间，越接近地表，热传导速率越大，温度传播越快，且影响深度大概为地表以下7～10 m。

3.2 计算的空间和时间精度分析

通过改变时间边界条件以及分层设置参数，将模拟结果与测量结果进行对比，模拟精度变化的计算公式为：

3.2.1 空间精度分析

在模拟时通常采用统一的热扩散系数，而实际地层并不均匀，如表1所示，因此势必会对结果造成误差。若考虑分层的影响，则分层设置参数，如图7所示，模拟得到的实际结果更接近于实测值。同时Ts和Tlayer的结果表明二者仅在浅部差异较大，而对深部影响不大，说明该段时间内热扩散系数的改变只对浅部地热传播影响显著。与Ts相比，对于Z1孔，一般在地表以下0～4 m处，Tlayer降低0.2～1℃，平均模拟值降低0.42℃，精度提高了2.47%；对于Z2孔，在地表以下0～1.2 m处，Tlayer降低0.1～0.8℃，平均模拟值降低0.26℃，精度提高了2.03%；对于Z3孔，在地表以下0～4 m处，Tlayer增加0.2～1℃，平均模拟值增加0.74℃，精度提高了3.57%，表明分层设置热扩散系数时精度能够提高2%～4%。Z2之所以影响误差深度较小，是由于浅部地层与整个地层热扩散系数的均值相近，而且传热影响最大也在浅部。结果表明一般影响深度为0～4 m，且与地层之间热扩散系数的差异性有关，若浅部地层差异越小，采用平均热扩散系数时模拟结果越准确。

3.2.2 时间精度分析

通过所测数据计算地表日平均温度以及月平均温度，分别将其作为上边界条件得到模拟温度Tday和Tmonth，如图7所示。当以日平均温度为上边界时，与Ts相比，模拟结果整体变化不大，二者曲线几乎重合，说明采用日均温度对实际模拟结果的影响不大。而以月平均温度模拟时，仅浅部的模拟结果有差异，而深部的模拟结果几乎不变。相对于Ts而言，Z1孔在地表以下0～1.6 m处时，Tmonth增大0.1～1℃，平均值增加0.4℃，精度降低2.22%；对于Z2孔，在地表以下0～5 m处时，Tmonth增大0.1～1℃，平均值增加0.44℃，精度降低2.54%；对于Z3孔，在地表以下0～1 m时，Tmonth减小0.1～1℃，平均值降低0.32℃，精度降低2%，表明上边界温度采用月均温度时使得模拟结果精度降低2%～3%。Z2孔相对Z3孔岩层较为复杂，且其精度也相对较低，说明以月平均温度作为上边界时，地层岩性越均匀，对模拟结果的影响深度越小，而当地层较为复杂时，则对模拟结果的影响较大。

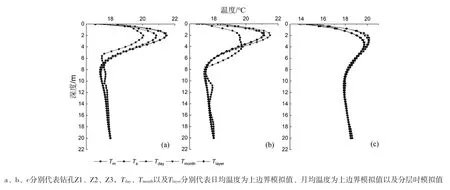
图7 温度—深度剖面图Fig. 7 Temperature-depth profiles

以上结果表明无论时间精度的改变还是空间精度的改变，对于模拟结果的影响在浅部0～5 m处，考虑到实际测温的困难性，采取热扩散系数均值以及日均温度即可保证模拟结果的准确性，此外，地层均匀，地层间热物理性质差异越小，所得的模拟结果也越精确。

3.3 浅层地温预测

利用所测11月份后2个月iButton温度，对2个月后对应时刻温度进行预测，可得2020年1月初对应时刻温度，并将其与之前所测7月底和11月初温度进行对比，所得结果如图8所示。事实上，这三个月份可分别对应一年内夏、秋、冬季的温度随深度变化规律。Z3孔泥岩传热较快，深部不同季节温度相差较大，而另外两孔相差不大。夏季地表温度高，而秋、冬季地表温度较低，为达到恒温层温度，夏季随深度增加温度逐渐降低，而秋、冬两季则随深度增加温度逐渐上升，因此二者的温度—深度曲线不同。同时也反映了地下水的渗流特性，夏季雨水多，渗透速率整体向下，温度梯度随深度逐渐增大（邓孝等，1989；Kurylyk et al,.2014）。地表温度与季节变化紧密相关，对应夏季＞秋季＞冬季，对于较深处6～12 m则为冬季＞秋季＞夏季，反映了温度向下传播的滞后性，同时也表明季节变化对热传递的影响深度大概位于地表以下 10～15 m。

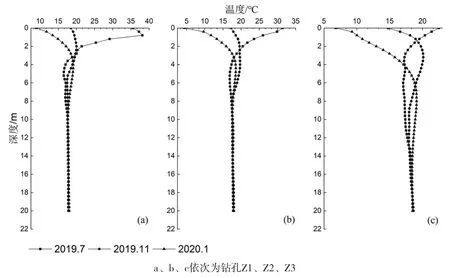
图8 不同季节温度—深度变化示意图Fig. 8 Temperature-depth curves in different seasons

4 结论

（1）对于季节性的地温预测，利用iButton获得的高精度连续地表温度，能够更加接近实际的温度状况，模拟结果表明地表温度变化对于地温的影响深度能达到地表以下7～10 m处。

（2）Z1、Z2和Z3孔采用分层热扩散系数对模拟结果的影响深度位于地表以下0～4 m，模拟结果改变0.1～1℃，精度分别提高2.47%、2.03%和3.57%。采用日均温度来模拟地温能够保证较高的精度，而以月平均温度得到的模拟地温误差主要在地表以下0～5 m，模拟结果改变0.1～1℃，精度分别降低2.22%、2.54%和2%，且三钻孔不同的影响深度也表明地层越均匀，误差越小。由于仅考虑季节性温度的传播深度，分层设置热扩散系数仅能降低浅部0～4 m的模拟误差，此外，以月均温度作为边界条件会增加浅部0～5 m的模拟误差，而日均温度影响不大。因此在保证模拟精度以及节约监测时间和成本的前提下，在实际应用中可以采用浅部地层0～5 m的分层热扩散系数，深部区的平均热扩散系数以及日均温度作为模拟的参数和边界条件。

（3）通过该模型预测冬季地温，得出季节性变化对于温度的影响深度为10～15 m，同时温度的传播也存在滞后性，且不同的传热模式与地下水垂向流向有关。