基于UP-Alinea的重庆市多车道汇入智能控制算法研究
陈晓利, 蒋淘金, 张磊
(1.重庆交通大学 交通运输学院, 重庆 400074;2.招商局重庆交通科研设计院有限公司 自动驾驶技术交通运输行业研发中心, 重庆 400067;3.重庆市公安局 交通巡逻警察总队 交通监控指挥中心, 重庆 400054)
典型山地环境特点导致重庆市道路交通存在路网级配不合理、干道交通流量集中、重要节点拥堵严重、路网韧性差的缺陷,严重制约了重庆市经济的高速发展,需从系统的层面在城市交通典型瓶颈路段进行交通控制,缓解交通拥堵。城市立交作为车流通行的重要节点,支撑着大量城市交通出行。但在多车道汇入区域,由于匝道口交织区密集的车辆换道与汇入极易造成交通拥堵,通行能力大大降低。同时汇入区车辆的频繁起停及长时间延误,使车辆发动机油耗显著增加,不利于城市空气污染治理,多车道汇入区域成为城市交通治理的重点目标。
1 研究现状
为降低多车道汇入区域的交通拥堵,增强汇入交织区的通行能力,国内外学者对多车道交通汇入控制进行研究,形成了很多理论成果。从传统交通控制方法来看,主要包括静态交通控制和动态交通控制。静态交通控制方法主要包括固定配时信号灯、限速标志、诱导标志、车道标线、安全护栏等,对这些交通设施的不同功能进行组合,可从道路设计源头把控多车道汇入区域的交通控制,是交通诱导控制的物理基础。该方法最早于1963年在美国芝加哥的州级高速公路匝道得到应用,结果表明入口匝道的车速得到显著提高,并缓解了交织区的交通冲突。从此固定配时信号灯控制得到广泛应用。动态交通控制利用可变配时信号灯、可变交通信息板、车道指示灯等交通设施,通过各类信号的动态转变传达交通控制信息。不同于静态的交通标志标线,动态交通控制可根据实时交通流密度、速度等信息通过设定好的控制算法实现有针对性的多车道汇入区域交通控制。
在动态信号灯配时领域,Wong C. K.等通过将车道传感器实时收集的车头时距、车道占有率等参数带入匝道区域道路线位、线形等几何空间约束中,采用车道级控制算法动态输出配时方案。刘伟等将干道交织区作为研究对象,通过不同相位控制方案的交通效率对比,研究最优动态配时算法。结果表明,可变交通信息板可通过显示不同限速值改变汇入前不同车道的区间速度,调整汇入交通流量。Knoop V. L.等的研究结果表明,可变交通信息板不仅可改变汇入前车辆的速度,还可通过限速增加车道空间占有率,降低汇入前后车速改变量,从而提高交通安全水平并缓解交通拥堵。Papageorgiou M.等基于Alinea算法,通过控制汇入后道路占有率实现多车道汇入区域的动态交通控制。
为验证不同多车道汇入交通控制方法在山地城市立体交通中的适用性,探索符合山地环境特点的多车道汇入交通控制算法,该文选取重庆市公园立交多车道汇入路段进行交通流时空分析和交通控制仿真研究,在获取该路段几何参数与交通流时空参数的基础上,借助VISSIM7.0交通仿真软件建立道路几何模型,输入相应时空交通流参数,对比分析无信号控制、固定配时信号控制、UP-Alinea动态信号控制3类多车道汇入交通控制方案。
2 多车道汇入交通控制算法
2.1 多车道汇入控制的原理与目标
受山地环境高差变化大、桥隧占比高、布局受限多等的影响,山地城市立体交通在多车道汇入区域的车道数量、线形等道路几何参数与车辆速度、密度、流量等交通流参数与平原城市存在显著差异。多车道汇入交通控制多通过信号灯的相位状态引导不同车道可通行的交通流量,进而提高汇入匝道区域的通行能力。由于早晚高峰期主路与汇入匝道的交通量均显著增加,多车道汇入区域的通行效率下降,若汇入后车道数量低于汇入前主路与匝道之和,则会使汇入区大量车辆产生换道行为,导致交通拥堵程度恶化。为提高多车道汇入区域的通行效率,在主路与匝道的相应车道区域设置信号灯,通过限制上游交通量对汇入区域的冲击,保持汇入区域始终处于最佳交通流密度和速度状态,保证多车道汇入区域的通行效率。
2.2 多车道汇入定时控制算法
为探索符合山地环境特点的多车道汇入交通控制算法并验证其有效性,引入2类常见多车道汇入控制算法:一类是静态信号灯固定配时控制算法,另一类是Alinea动态信号灯控制算法。
信号灯固定配时控制算法最早由Wattleworth J. A.在1965年提出。该算法通过收集路段1 d内交通流参数变化及对历史数据的估计,得到交通流参数的演化特征。以主路上交通流不高于其通行能力为边界条件,以汇入该主路的匝道通行能力最大化为目标函数,则第j个汇入区域的流量qj的稳态模型为:
最优控制策略为:
式中:aij为在汇入匝道i进入主路并通过j路段的交通流比例;r为匝道汇入调节系数,代表单位时间内匝道汇入主路的车流量;ri为汇入区调节比例;qcap,j为j路段的通行能力;rmin,j为汇入区最小调节比例;rmax,j为汇入区最大调节比例。
该算法的交通流量仅考虑历史数据的评估平均值,没有考虑1 d内交通量随着时间而出现的高低起伏的变化。因此,有学者对其进行改进,以15~30 min的间隔为一个控制算法周期分段部署,得到固定配时信号灯控制算法的配时公式:
式中:C为一个完整相位的时间周期;n为汇入前匝道的车道数量;m为每个相位允许放行车辆的车道数量。
在计算得到一个完整相位的时间周期C后,根据各车道的车流量确定一个周期内的绿信比。
2.3 多车道汇入UP-Alinea控制算法
Alinea动态信号灯控制算法最初来源于比例-积分-微分控制控制器(PDI)中积分控制器模型,数学表达式为:
(1)
式中:e(t)为误差函数,e(t)=oexp-oout(t);oexp为汇入后主路期望占有率;oout(t)为第t个积分时窗汇入后主路的占有率。
对积分控制器模型求导得:
r(t)=K′Re(t)
(2)
令KR=K′RT,将式(2)离散化后得:
R(m)=R(m-1)+KR[oexp-oout(m)]
式中:R(m)为第m个积分时窗的汇入匝道调节比例;R(m-1)为第m-1个积分时窗的汇入匝道调节比例;KR为调节参数,为常数;oout(m)为第m个积分时窗汇入后主路的占有率。
Alinea信号灯控制算法需要汇入后主路占有率数据oout(m)。实际工程应用中,为降低成本,减少传感器安装数量,可只在多车道汇入区域前安装车流量检测器,进而发展出UP-Alinea信号灯控制算法。该算法通过检测多车道汇入前的车流量数据估计多车道汇入后车流量、占有率等参数。将多车道汇入后的车流量近似看作汇入前各车道车流量之和,得到多车道汇入后占有率估算公式:
(3)
式中:oin(m)为主路多车道汇入前的占有率;qramp(m)为匝道多车道汇入前的流量;qin(m)为主路多车道汇入前的流量;λin为主路多车道汇入前的车道数量;λout为主路多车道汇入后的车道数量。
将多车道汇入后占有率估计值oout(m)exp作为Alinea信号灯控制算法的输入参数,得到UP-Alinea信号灯控制算法:
R(m)=R(m-1)+KR[oexp-oout(m-1)exp]
(4)
3 多车道汇入路口交通流分析
3.1 多车道汇入路口概况
重庆市公园立交东侧通过武江立交连接内环快速路,西侧通过大农立交连接双碑嘉陵江大桥,是通往双碑大桥的重要节点。主路方向为石马河立交往双碑大桥方向,匝道方向为武江立交往双碑大桥方向。汇入前主路为三车道、匝道为三车道,多车道汇入后主路为四车道,车道宽度3.5 m。由于该路段承接重庆市中部槽谷与西部槽谷日常交通出行的较大车流量的过境,早晚高峰期极易产生拥堵,对内环快速路和双碑隧道的正常运行产生不利影响。公园立交多车道汇入条件见图1。
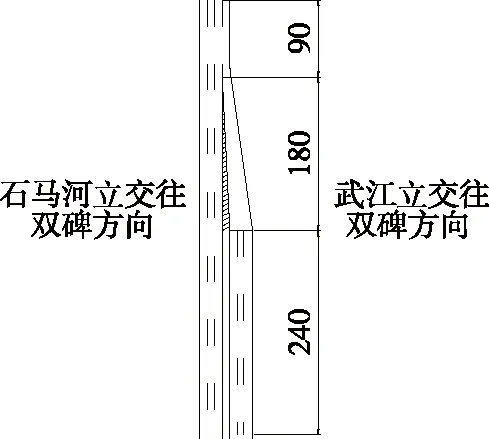
图1 公园立交多车道汇入示意图(单位:m)
3.2 多车道汇入路口交通流分析
通过交通调查,得到公园立交汇入路口2020年11月24日每小时交通流量分布数据,包括主路石马河立交往双碑大桥和匝道武江立交往双碑大桥方向的客车、公交车、出租车、非营业车辆、货车等车型的交通流量。根据《公路工程技术标准》,按表1所示折算系数将其换算成标准车型的当量交通量(见图2、图3)。

表1 各车型交通当量折算系数
从图2、图3可看出:在0:00—7:00时段,无论是主路石马河立交往双碑大桥方向还是匝道武江立交往双碑大桥方向,各车道的交通流当量均处在较低水平;在7:00以后,主路石马河立交往双碑大桥方向的交通流当量快速增长,且15 h内交通流量未明显下降,均在高位运行,在22:00之后交通流当量出现显著下降;匝道武江立交往双碑大桥方向的交通流当量在7:00快速增长,在12:00后显著下降,全天只出现一次早高峰期,晚高峰期增加不明显。

图2 石马河立交往双碑大桥方向交通当量分布

图3 武江立交往双碑大桥方向交通当量分布
4 多车道汇入交通控制仿真分析
4.1 交通流当量与车道占有率
根据式(3),采用动态UP-Alinea信号灯控制算法需要已知主路多车道汇入前的占有率oin(m),而在前期数据获取阶段得到的参数为交通流当量,需进行转换。根据车道占有率的定义可知:
式中:L为平均当量车辆长度;K为车流密度。
根据速度-密度线性方程[见式(5)],可得到交通流当量与车道占有率的关系式[见式(6)]。
Q=Kv=K(aK+b)=aK2+bK
(5)
(6)
式中:a、b为常数项。
根据文献[18]给出的检验结果,得a=-1.26、b=105.17。交通流当量与车道占有率的换算公式为:
Q=-35 000O2+17 528O
(7)
4.2 VISSIM仿真模型
采用VISSIM7.0对公园立交石马河立交往双碑大桥与武江立交往双碑大桥方向的车流量进行交通仿真,仿真模型见图4。

图4 公园立交多车道汇入仿真模型
4.3 仿真评价指标
以主路的平均车速与路程耗时(通过多车道汇入区的时间)表征主路的交通状态;以匝道车辆的平均延误和最大排队长度表征匝道的交通状态;以路网平均延误时间作为整体路网的交通状态评价指标,路网平均延误由主路和匝道的延误组成。
4.4 不同控制方案对比分析
将无信号控制、固定配时信号控制、UP-Alinea动态信号控制3类多车道汇入交通控制方案应用于公园立交多车道汇入控制,通过对比主路平均车速与路程耗时、匝道车辆平均延误和最大排队长度、路网平均延误时间评价3类控制方案的效果,结果见表2。
从表2可看出:1) 采用UP-Alinea动态控制时,公园立交主路平均车速最高,为50.6 km/h;其次为固定配时控制的48.2 km/h;无信号控制时,由于匝道汇入车辆的干扰,主路车速显著下降,仅为44.5 km/h。2) 相比无信号控制方案,采用固定配时信号控制与UP-Alinea动态信号控制,主路车辆路程耗时在7:00—9:00高峰期分别降低6.6%、11.1%,匝道平均延误在高峰期分别降低12.1%、15.0%。但信号灯的设置会造成匝道出现排队现象,UP-Alinea动态信号控制方案的排队长度为103.8 m,优于固定配时信号控制方案的124.6 m。3) 采用UP-Alinea动态信号控制时路网平均延误最小,其次为固定配时信号控制方案,无信号控制时延误最大。

表2 3类交通控制方案仿真结果对比
5 结论
(1) 重庆公园立交主路在早高峰7:00以后交通流当量快速增长,且之后15 h内交通流量未明显下降;匝道交通流当量在7:00以后快速增长,在12:00后显著下降,全天只出现一次早高峰,晚高峰期增加不明显。
(2) UP-Alinea控制算法通过合理估计汇入后车道占有率进行交通控制,只需汇入前各车道占有率数据,控制算法的实现难度大大降低。
(3) 从主路交通效率、匝道交通状态和路网交通状态等维度提取交通控制评价参数,采用VISSIM7.0进行交通控制仿真,结果表明从路网延误来看,UP-Alinea动态信号控制算法最优。

