基于规划模型对生产类企业原材料采购问题的研究

杜亚冰，李 科，范明千，严佳慧

(1.河南城建学院 数理学院，河南 平顶山 467036；2.建筑光伏一体化技术河南省工程实验室，河南 平顶山 467036；3.河南城建学院 计算机与数据科学学院，河南 平顶山 467036)

长期稳定的盈利能力是衡量一家企业优质与否的最基本标准[1]。生产类企业的利润主要受产品的生产成本、产品定价及销量等因素制约[2]，其中，企业采购成本会因原材料的多样性及配比的随机性影响而出现波动，从而影响企业利润。因此，优化原材料采购及配比方案是降低生产成本、提高企业利润、提升市场竞争力的有效手段。

本文以某建筑和装饰板材生产企业为例，利用熵权法[3-5]判断402家原材料供应商各指标权重，从中筛选优质供应商，结合0-1规划[6-7]、多目标规划[8]模型优化原材料采购及配比方案，并与过去5 a历史数据进行比对，发现优化后的方案可以有效降低企业生产成本，提高每万元产量，从而增加企业利润。

1 企业生产概况

该企业主要以木质纤维类材料为原材料生产建筑和装饰板材，企业年生产周期为48周。为了保障原材料供应，通常需提前24周制定采购计划并确保有2周的仓储量。经市场调研发现该公司主要采购3种类型原材料，分别是实木板(A)、胶合板(B)和细木工板(C)。历史数据显示在过去5 a(共计240个工作周)中共有402家供应商为该企业提供过原材料。

由于不同类型原材料的生产效能不同。该企业周产能为28 200 m3，如果全部使用实木板，每生产1 m3产品需消耗原材料0.60 m3；如果全部使用胶合板，每生产1 m3产品需消耗原材料0.66 m3；如果全部使用细木工板，每生产1 m3产品需消耗原材料0.72 m3。不同类型原材料的采购单价也不同，细木工板的市场价约为100元/m3，而实木板和胶合板的市场价分别比细木工板高出约20%和10%。

由于运输费用只与货物重量有关，因此3种类型原材料的单位运输费用基本相同。

2 数学建模与数据处理

2.1 参数定义

为了方便描述，文中使用了一些参数，其符号及定义见表1：

表1 各参数符号及定义

2.2 数据预处理

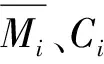
(1)

(2)

其中，mj、nj分别表示各供应商历史每周供应量和采购量，t表示供货周数。

第三项指标fi表示供货频率，用于反映不同供应商在过去5 a(共计240个工作周)供货的连续性。考虑到Matlab对数据处理的高效性和准确性，其结果可以利用Matlab软件通过运算过去5 a的供货次数来得到，运算程序如下：

A=xlsread(‘240周各供应商供应情况’);%导入240周各供应商供应数。

for i=1:402

B(i)=sum(A(i,:)>0);%计算各供应商供应次数。

end

2.3 熵权法筛选优质供应商

2.3.1 数据分析与计算

企业为了保障生产原材料的稳定供应，采取广泛选择、部分优先的供应商筛选策略，即采用评判算法从全部402家供应商中筛选出50家优质供应商(结合企业生产情况拟定)，给予优先供货权。

①熵权法是一种客观赋权方法，相比层次分析法等主观赋权法结果更精确，更可靠。

②熵权法能够深刻反映指标信息熵值的效用价值，从而确定权重，这种算法思想与企业未来可持续优化供应商策略有相似之处。

③熵权法算法清晰，适应性强，可以覆盖到同类问题，使本文结论具备较好的推广价值。

熵是一个热力学概念，用于度量系统的无序性。熵值越大表明系统越混乱，携带信息量越少；熵值越小表明系统越有序，携带信息量越多。通过计算熵值可以判断某个事件或某项指标的离散程度，如果得到的熵值越小，说明该项指标的离散程度越大，那么该指标对综合评价的影响(即权重)就越大。

对3项指标分别进行归一化处理，见式(3)，再计算3项指标各数据占总体的比重pij、熵值ej和权重wj[9]，见式(4)～式(6)：

(3)

(4)

(5)

(6)

其中，xij代表各供应商在不同指标下的数值。

由于篇幅限制，此处仅将3项指标的熵值ej和权重wj计算结果列出，具体见表2。

表2 各指标熵值和权重结果

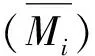
2.3.2 结果呈现

结合表2，利用公式(7)计算供应商各自综合得分：

(7)

由于篇幅限制，此处仅列举了402家供应商中的120家，其ID和综合得分见表3。

表3 部分供应商综合得分

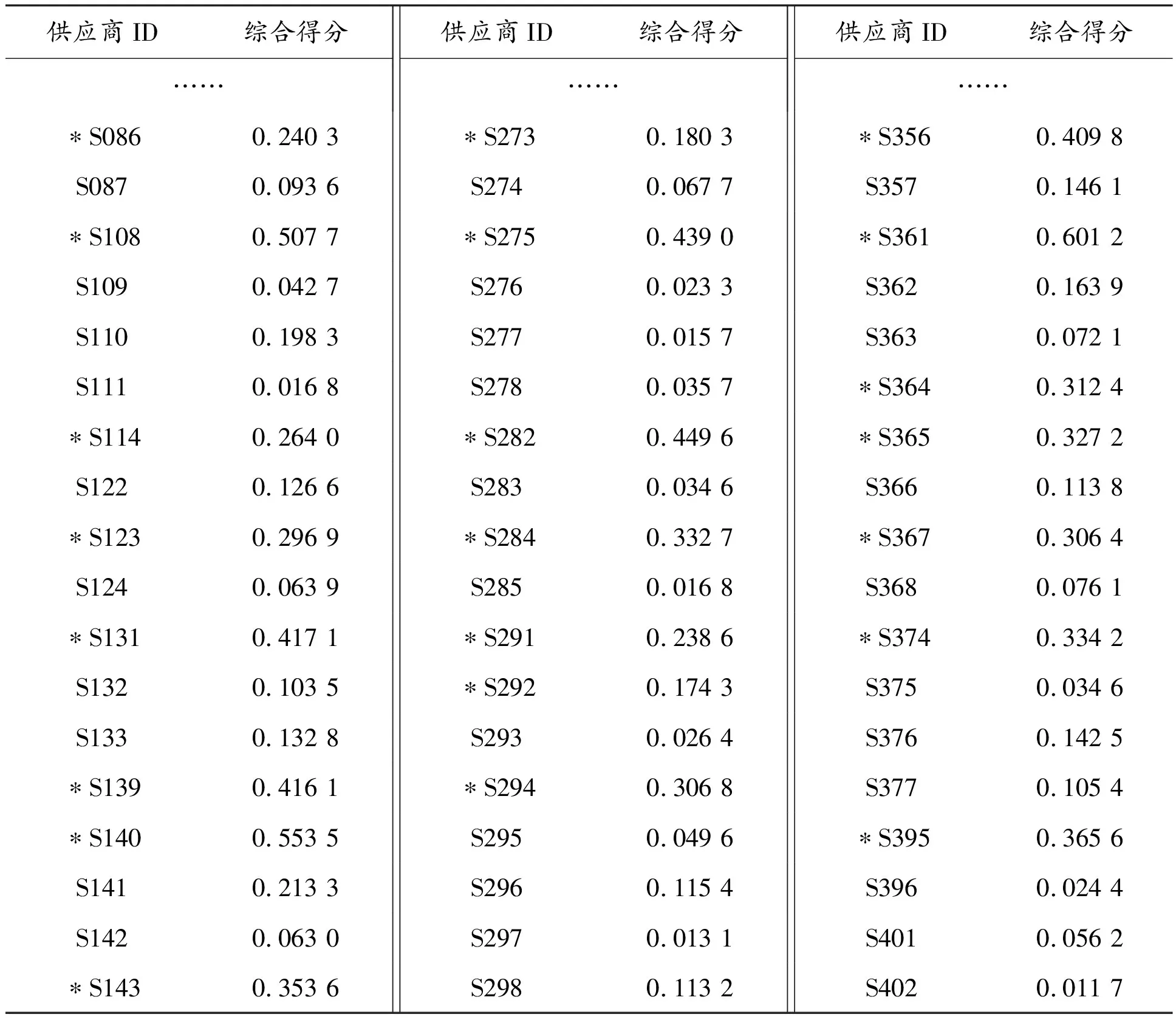
续表3

为了筛选出50家优质供应商，制定以下筛选条件：

①将周平均供应量低于26 m3的供应商舍去(26 m3是402家供应商周平均供应量)；

②将供货完成度低于50%的供应商舍去，目的是确保企业始终有2周的仓储量。

③按综合得分从高到低筛选供应商，直至选满50家。

通过筛选，得到50家优质供应商，其综合得分和ID见表3中“*”。

2.4 利用规划模型获取最佳采购方案

企业的生产成本由采购成本、转运成本两部分组成，其中采购成本的优先级大于转运成本[10]，因此选择用最低的采购成本去限制转运成本是合理的。

为了获取最佳采购方案，建立0-1规划模型，结合不同类型原材料的定价和供应商的供应能力，利用LINGO软件对全部402家供应商进行计算求得最低采购成本。

转运成本和货物数量有关，生产单位产品时消耗实木板(A)最少，细木工板(C)最多。由采购单价和生产所需得到胶合板(B)的生产成本是最高的。为了降低转运成本，利用多目标规划模型，在尽可能达到最低采购成本的前提下，选择尽可能多地采购实木板(A)，尽可能少地采购细木工板(C)，尽量不采购胶合板(B)的方案，求解最低转运成本，并获取周采购最优方案。

2.4.1 利用0-1规划模型获取最低采购成本

①约束条件：采购方案必须保证企业的正常生产需要，即每周的产量大于28 200 m3。

(8)

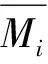
同时在0-1规划模型中，用“1”表示选择该供应商，“0”表示不选择。

X=(xi)1×402,xi=1 or 0

(9)

其中，xi代表各供应商，i=1,2……402。

②目标函数：目的是制定未来24周每周最经济的原材料采购方案，因此要在保证周产能的基础上尽量减少采购金额，即

(10)

其中，Y表示采购原材料的总金额，pi表示各供应商原材料总价格。

2.4.2 利用LINGO软件求解最低采购成本

LINGO(Linear Interactive and General Optimizer)即“交互式的线性和通用优化求解器”。LINGO拥有一整套快速、内建求解器，会自动读取方程式并自动选择合适的求解器，可以简洁、高效地建立和求解线性、非线性以及整数规划模型，是求解优化模型的最佳选择。

结合式(8)～式(10)，利用LINGO软件对该0-1规划模型进行求解。代码如下：

model:

sets:

gc/1..402/:D,P,x;

endsets

data:

D=@OLE('C:UsersDesktop402综合得分.xlsx','A');

P=@OLE('C:UsersDesktop402综合得分.xlsx','B');

enddata

min=@sum(gc(i):D(i)*x(i));

@sum(gc(i):P(i)*x(i))>28200;

@for(gc(i):@bin(x) );

Y=@sum(gc(i):P(i)*x(i));

end

求解得到每周最低采购成本约203.12万元人民币。

2.4.3 利用多目标规划模型获取最低转运成本

与线性规划模型相比，多目标规划模型引入了正负偏差变量d+、d-，来衡量每个目标的完成情况。

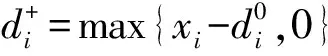
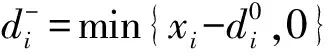
①约束条件：为了保证企业正常的生产运营，周产能必须达到28 200 m3，即：

(11)

由于最低采购成本约203.12万元人民币，因此在求解最低转运成本时要确保其对应的采购成本尽量不大于该值，即：

(12)

历史数据显示各供应商每周供应实木板的总量为9 916 m3，由前文分析可知，应尽可能多采购实木板(A)，少采购细木工板(C)，因此设置约束条件如下：

(13)

(14)

其中，xA、xc分别表示实木板和细木工板的采购量。

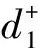
(15)

结合式(11)～式(15)，利用LINGO软件对上述模型进行求解，得到xA=9 916 m3，xc=8 404.8 m3,即周采购最佳方案为：每周采购实木板约9 916 m3，细木工板约8 404.8 m3。

3 结果分析与成果推广

3.1 最优采购配比方案

通过两步规划得到了周采购最佳方案，再以广泛选择，优先50家重要供应商为原则，从402家供应商中选出最优采购配比的组合方案，具体结果见表4。

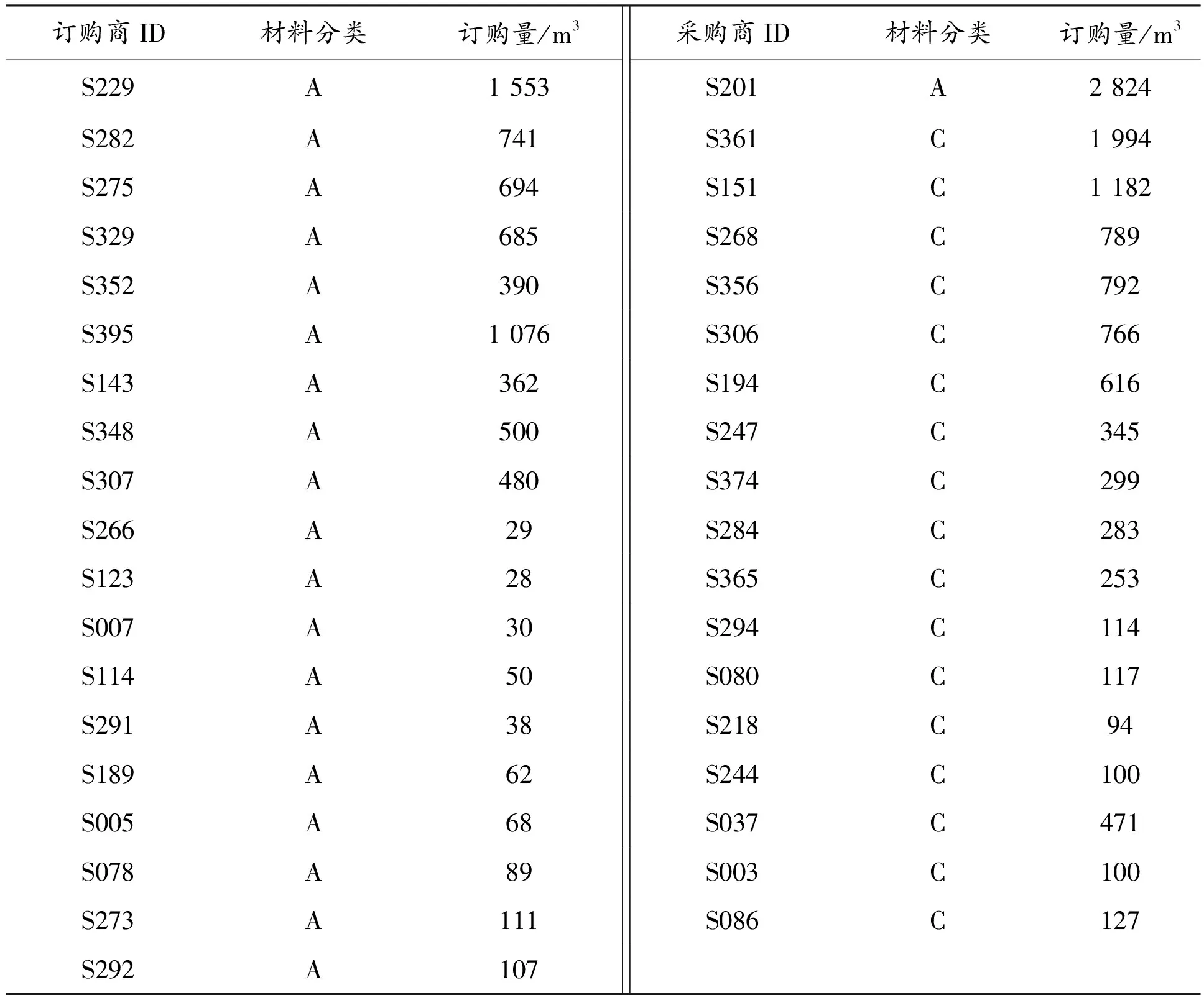
表4 最优采购配比方案

为了检验最优采购方案对提升企业生产效能的作用，将过去5 a年均每万元产量与规划方案预测的每万元产量进行对比，结果见图1。

(16)

由图1可以看出，最优采购方案的每万元产量(138.840 m3)比过去5 a平均值(115.724 m3)提升了23.116 m3,增长率约20%，有效提升了企业产能，降低了生产成本。

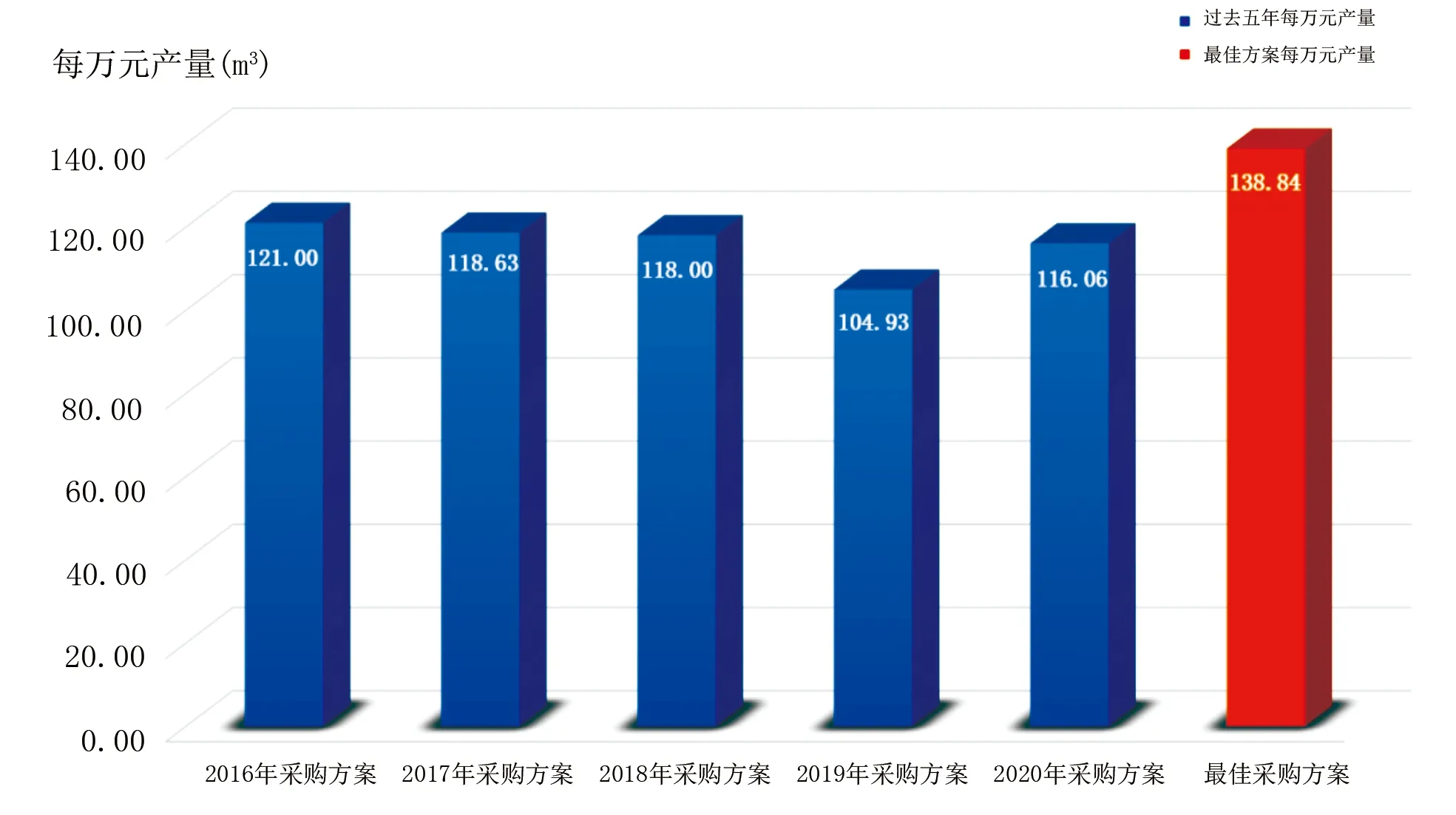
图1 历史方案与优化方案对比图

3.2 结论与推广

3.2.1 结论

以某建筑和装饰板材生产企业为研究对象，利用熵权法有效筛选优质供应商，采用0-1规划和多目标规划模型控制不同类型原材料采购成本、配比方案及转运成本，通过数学建模，计算得到最优采购方案，并与历史数据进行了比对，最终得到以下结论：

(1)采用熵权法对供应商进行量化评价，筛选优质供应商以提高原材料供应的稳定性是可行的。

(2)利用0-1规划模型获取最低采购成本，结合LINGO软件求解得到最低采购成本约203.12万元人民币。

(3)利用多目标规划模型获取最低转运成本，结合LINGO软件求出最优采购方案，即每周采购实木板9 916 m3，细木工板8 404.8 m3。

(4)利用系统性规划模型可以有效降低该企业生产成本，从而提升企业利润。

3.2.2 推广

本文以生产类企业为例，通过数学建模、控制变量、归一化处理等手段，达到优化原材料配比、量化供应商评价、优化采购方案的目的，有效提升了企业产能、降低了生产成本、增加了市场竞争力。其建模方法同样适用于现实生活中的各类企业和生产单位，具有一定的现实推广意义。