一线救治伤员后送资源配置策略研究

邵 辉, 黄朝晖

(1.陆军军医大学 陆军卫勤训练基地卫生勤务学教研室,重庆 沙坪坝 400038; 2.海警医院卫勤处,浙江 嘉兴 314000)

0 引言

战场一线救治是分级救治的前提和起点，是保障作战胜利的需要[1]。良好的一线救治组织不仅能够提升救治效率，还可以有效避免伤员二次负伤，这对鼓舞部队士气、增强战斗力、保障作战的胜利有重要影响[2]。因此，无论是各级指战员还是卫生人员都应对一线救治的组织开展提起高度重视。本文通过整理国内外作战一线救护资料，综合探讨合成旅一线营连救护伤员收拢后送过程中运力配置及路径规划问题。

1 研究现状

1.1 一线伤员救治组织指挥

目前，对伤员救治和后送的研究大多集中在旅救护所及之后的过程，营、连一线救护模式尚未完善。我军关于“一线救治”的研究，自解放战争的经验总结中开始有报道[3，当时对其命名为“火线救护”，随后也有相关研究陆续跟进，但大多都是对历史作战的经验介绍，深入剖析较少。美军、印军、俄军对一线救治的重要性都有重点强调[4～6]。一线救治伤员是战伤分级救治的起点，现代战争可能在短时间内产生大量伤员，与以往相比，需要更多救护力量[1]。随着信息化军队的建设和发展，一线战损情况掌握的实时性、灵敏性更强，一线救治的组织方法、实施过程将发生实质性变革。

1.2 减员预计模型

合理的减员预计对作战指挥、组织筹划有重要指导意义[7]。目前公开发表的研究中，减员预计算法主要体现为三大类。第一类是基于传统算法[8,9]，第二类是基于多因子预测的算法[10,11]，第三类是基于系统仿真的算法[12]。传统算法操作简便，得出数据较宏观，更适用于战术级及以下单位的实际工作中使用；多因子预测方法只需构建基本数据库，便可方便使用；系统仿真算法具有可解释性，更适用于理论研究，后续兴起的基于模型的减员预计算法[13]正是基于此的。本研究在前序研究基础上，结合多因子算法、系统仿真算法，提出了基于地域概率的减员发生模型，为后续伤员的救治资源配置奠定基础。

1.3 运力配置及路径规划模型

关于运力配置的研究已有丰硕成果。李周清等[14]通过构建多目标优化模型，利用遗传算法求解海上战略投送动员民船多点选型问题，王书勤等[15]利用混合蚁群算法解决了军事定向越野路径优化问题。张巍等[16]设计了铁路运力资源优化配置决策支持系统。这些研究为探讨一线伤员收拢后送运力配置及路径选择提供了参考。

2 模型建立

为探究一线伤员收拢后送过程中运力配置和路径规划策略，首先需要模拟战场环境仿真产生伤员作为驱动因素。因此，本模型存在两个子模型。第一，伤员的产生模型，参考国内外战例和系列研究，首次提出基于地域概率的减员发生模型；第二，救护运力配置及路径优化模型，从连抢救和营救护两个层面对一线伤员的后送策略进行探讨。需要提出的是，考虑到大多数战斗历史经验报导与模型建立方便，一线伤员救护后送工作常在战斗间隙展开[17]，本模型对救护期间产生的新伤员忽略不计。

2.1 伤员产生

伤员的产生通常使用多因子预测和系统动力学方法[10,11,13]，此类方法利用宏观减员和局部蒙特卡洛的方法模拟减员，由历史数据、系统动力学关系构建，其操作过程跳过局部概率问题直接产生减员结果。本文提出基于地域概率的减员发生仿真模型，相比前者，该模型能够实时计算得出战场中各地域的减员概率，不仅可以指导卫生工作，也可以为作战筹划提供参考。此模型对数据依赖性较高，输入数据信息越详细，对战场各地域的减员概率预计越可靠，但经过简化部分步骤的数据输入，此模型也可以转化成经典的减员预计算法。主要步骤如下：

首先，对战场环境和参战人员或单位进行初始化。栅格化战场，将战场区域(长L×宽H)栅格化为长为L宽为H的栅格单元。根据实际交战类型，设定参战人员分布，包括密集型，分散型，队列型等。根据设定的人员分布类型，对第n个参战人员，第t时刻在战场区域L×H内，产生其位置信息Sn,t。

Sn,t=f(n,t,L,H)

(1)

2.1.1 计算攻击位置概率

对于每种武器Wk，每一个栅格化单元Ui,j，都有攻击发生的概率pk,i,j,考虑不同武器对不同位置的打击随时间t的改变，建立某栅格单元Ui,j遭受武器Wk在t时刻遭受打击的概率Pk,t,i,j的计算模型如下:

(2)

其中，Wk(t)为t时刻第k种武器攻击i,j地区的概率较基准概率Pk,i,j的变化情况；Cons(k)为第k种武器的攻击概率变化常数，当其值为1时，代表该武器的攻击概率为一定值，若为0，则代表概率可变。

2.1.2 攻击半径

Rk～N(μ,σ2)

(3)

2.1.3 致伤概率

对于某武器k，有随机杀伤半径Rk，在杀伤半径内并非全部致伤，即使致伤，伤情伤势也不尽相同。这可以用致伤等级、倒计时表示，假设伤情变化仅与时间、接受处置有关。可以模拟在整个后送过程中的伤情变化。

2.1.4 伤员产生

通过以上步骤计算出的基于武器与位置的致伤概率，结合初始化的参战人员位置信息，对各参展单位进行受伤概率赋值。基于该概率，利用蒙特卡洛算法进行仿真，每次仿真都产生一种战斗情景，对应特定的伤亡情况。

Pn,t=g(Sn,t,Pk,t,i,j),[i,j]=Sn,t

(4)

2.2 救护规则设置

2.2.1 连伤员救治与移动

实施火线抢救工作的是连抢救组，它是连队建立的临时性救护组织。连抢救组一般在连首长的领导下，以卫生员为骨干，抽调卫生战士及其他后勤人员组成[18,19]。主要职责为：①迅速寻找发现和隐蔽伤员；②及时准确地实施救护；③积极组织后送。连抢救组视应情况选择“抢”与“救”的顺序，敌情突出，受敌火力威胁大时，先隐蔽伤员至伤员集中点，反之先救治伤员[2]。

伤员集中点是战场一线地域伤员初步集中、隐蔽的临时站点，一般在根据战斗队形、地形在战前设置[20,21]。设置原则为：①靠近部队通路；②避开火力杀伤区；③尽量便于寻找。伤员集中点的开设可以先后开展几处，但不宜过多。

伤员根据负伤情况，收拢到伤员集中点的流程不同。轻伤伤员一般可自行前往伤员集中点，中度伤和重伤伤员一般需要抢救组的初步急救和担架运送。这对抢救组提出了更高要求：①根据伤员发生情况，将救护组分组，分派至不同伤员集中点附近；②对每一个伤员集中点，组织附近中、重伤员搜寻、救治与收拢。

2.2.2 营伤员前接

营救护站一般在营首长领导下，以卫生排人员为基础，抽调其他人员组成。主要负责：①组织领导各连火线抢救，迅速将伤员从各连阵地上运回；②补充纠正连的急救；③做好后送伤员的准备，积极联系后转等[18]。营救护站以前接伤员为主，补充急救为辅，重点工作为快速将伤员后转。因此，前接与后转伤员的效率对营救护站来说尤为重要。

2.3 救护运力配置及路径优化

救护运力在本研究中主要包括车辆运输(运输车、急救车)、担架运输(担架组，每组2～4人)等，连救护运力与营救护运力分开计算。以①重伤员等待时间尽可能短，②总救治后送任务时间尽可能短为优化目标，建立营连救护运力配置优化模型。

2.3.1 连救护运力配置

在区域Z中，设置多个伤员集中点Jij,为使得所有伤员按照病情程度快速聚集到伤员集中点，抢救组应该做出以下措施：①优先救治和搬运重伤员；②选择向恰当的伤员集中点转移。

以初始设置的伤员集中点为中心，利用最近邻分类器，对所有伤员进行归类，将所有伤员对应分配到距离最近的伤员集中点。轻伤员可自行前往伤员集中点，中、重伤员视为卧位伤员，担架组按照伤员严重程度与距离顺序进行搬运，优先搬运距离较近的重伤员。在实施过程中，按照各集中点的搬运量的不同，以总搬运距离为参考，对各集中点搬运力量进行统筹分配。

2.3.2 连伤员集中点的更新

随着战斗的推进，减员发生的理想聚类中心与伤员集中点的相对位置会发生变化，当此距离差距超出规定上限时，则应更替伤员集中点位置，即在新的聚类中心附近寻找合适的伤员集中点。新的聚类中心计算方法如下：选定合理的伤员集中点数量k作为聚类中心数，利用基于欧氏距离的改良K-means聚类算法，计算伤员分布的k个聚类中心，作为伤员集中点位置。欧氏距离计算公式如下:

(5)

不同于一般K-means聚类算法的是，本算法对每一个聚类中心(备选伤员集中点Jij)迭代的运算过程，需要考虑其到营救护站的距离disted(Jij,Y)。即伤员经过某伤员集中点Jij，能够满足从受伤地点Sis到营救护站Y的距离disty(Jij,Y)=distl(Jij,Sis)+distl(Jij,Y)最短时，则该伤员被送至该集中点。改良K-means聚类算法的聚类中心迭代过程如下:

Step1随机选择k个伤员位置，作为聚类中心Jo,ij，规定收敛偏差阈值E;

Step2计算所有伤员到各聚类中心的距离，再计算该伤员经过该集中点至营救护站的距离disty；

Step3对每一伤员位置Sis，选择满足其disty最小的伤员集中点，并归到该类别，将归到同一类的伤员位置记录在LSo,ils,(ils=1,2,…,k)中，每类别所含点数计为NLSo,ils；

Step4对归类完成的k类伤员位置计算均值，作为新的聚类中心Jo+1,ij；

(6)

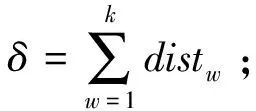
Step6重复Step2～Step5，直至δ≤E。

2.3.3 营救护运力配置及前接路径规划

营救护站主要任务为前接伤员，因伤员分行走伤员与担架伤员，在运力计算时需要考虑其对车辆的要求。假定一辆运输车可运输12名卧位伤员或20名行走伤员，一辆急救车可运输2名卧位伤员或8名行走伤员。在救治后送过程中，重伤情或卧位伤员优先。

使用TOPSIS综合评价方法[22]，对于各伤员集中点进行优先性评价，评价参数涉及重伤员数量Nz,ij、伤员集中点的危险程度Riskij、交通便捷度Tij，评价得分高的集中点优先前接。TOPSIS综合评价方法步骤如下:

Step1将k个集中点的q个评价指标按照如下公式进行归一化，得到归一化的矩阵Z:

(7)

(8)

(9)

Step3利用公式计算每个待排序方案与最优最劣方案的距离:

(10)

(11)

Step4最后得到各方面的评价得分D=D-/(D++D-)。

各伤员集中点前接优先顺序按照综合评价得分排好之后，按照各集中点伤员数量与运力关系，实行“蛙跳式”前接方法[4]。

3 模型验证

本文使用MATLAB构建战场环境并进行运力规划。以某假设地域红蓝双方交战为背景，模拟批量伤员产生，对红方连抢救组、营救护站的伤员救护与后送工作进行模拟和规划。红方三个连参与作战，共计500人。

3.1 参数设置

3.1.1 战场环境参数

为简化模型，以某平原地区4km×2km交战地域为例，模拟某种武器攻击。图1A中显示兵力部署初始情况，“*”即代表兵力，初始兵力围绕指定作战区域(阴影部分)随机分布，出现概率如背景色所示，白色代表出现概率高，黑色代表概率低。经仿真运算，减员概率分布如图1B中背景色所示，图1B中“o”展示某次仿真结果伤员发生情况，该营共500名兵力参战，单次战斗累计发生减员172名，减员率34.4%。

3.1.2 连、营救护组织参数

营救护站设运输车3辆，救护车2辆；各连共设伤员集中点5个，每伤员集中点设担架组5组。营救护站开设于[-500,-500]位置，连伤员集中点位置如图2所示。图2A中“*”代表伤员位置，五个“〇”代表五个伤员集中点，按图中所标数字顺序分别记为1～5号伤员集中点。图2B表示所有伤员被分派到距离最近的伤员集中点结果，相应伤员被标成与伤员集中点相同的灰度。

3.2 结果及讨论

3.2.1 各连救护力量使用策略

伤员产生后，按照各伤员集中点搬运任务量的不同，将搬运组进行了重新分配，如表1所示。

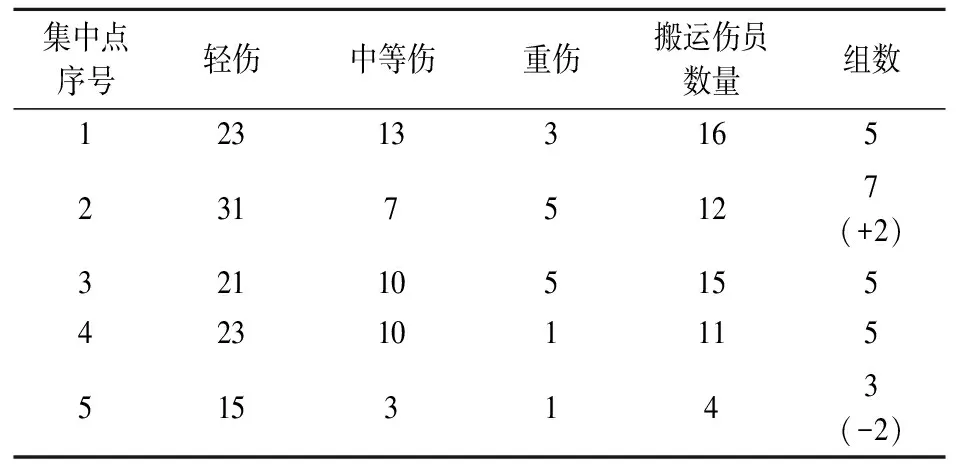
表1 各伤员集中点搬运组力量重新分配情况

各伤员集中点担架组使用情况如表2所示，各伤员集中点完成救治时间差距由43.8分钟缩减到9.6分钟，总体救治任务完成时间由71.5分钟缩短到55.8分钟，缩短了15.7分钟，效率提高22.0%。可见，实时感知伤员发生情况并对救治力量做出适时调整，能够大幅提高救治效率。

表2 担架组使用情况统计

作战阶段性结束后，假定红方占据优势，火线前移。根据新的减员预计情况，做出了伤员集中点迁移的方案，如图3所示。新的伤员集中点展开4处，按照图中数字标注为1～4号。按照就近原则，将原伤员集中点力量按照如下方案重新分配至新的集中点：1号→1号；2号→2号；3号、5号→3号；4号→4号。

3.2.2 营前接运力配置

对于根据各伤员集中点伤员囤积情况，营救护站合理派出运输车辆，按照优先顺序，以“蛙跳”形式完成所有伤员的前接[4]。各伤员集中点TOPSIS得分见表3。根据TOPSIS得分，各伤员集中点的优先顺序为1号→3号→2号→4号→5号。首先前接重伤员、其次中度伤，最后轻伤。同一伤情优先考虑评分。

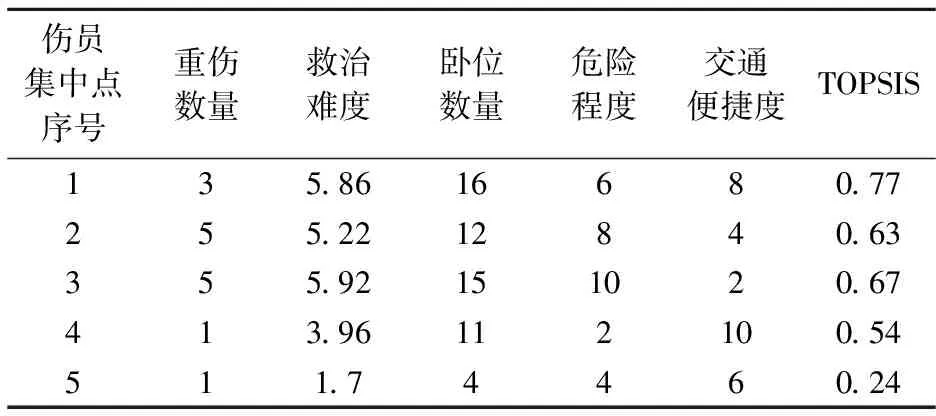
表3 各伤员集中点TOPSIS得分

综合考虑营、连救治的复杂性和战场情况多变性，若力求全局最优的优化方案则事倍功半，本模型采用逐步优化的策略灵活性强、实用性高，能够为一线救治组织指挥提供可靠方案。

4 总结与展望

随着信息化部队建设的加快，数学建模的思想在卫勤各个领域都有明显体现。在卫勤领域，关于减员预计、资源配置、工作流程优化等方面的研究日益兴起。一线救治是新时期军队的新课题，其组织体制的研究和改革是未来发展的必然趋势。基于信息化作战背景，模拟评估战场环境、优化协调伤员后送力量，将对一线救治实现信息化、自动化、智能化的统筹配置提供必要的技术支撑。