题目难度评估方法研究综述
许 嘉,韦婷婷,于 戈,黄欣悦,吕 品,2,3
1.广西大学计算机与电子信息学院,南宁530004
2.广西大学广西多媒体通信网络技术重点实验室,南宁530004
3.广西大学广西高校并行与分布式计算重点实验室,南宁530004
4.东北大学计算机科学与工程学院,沈阳110819
考试是区分学生能力和选拔人才的重要手段,在教育领域发挥着至关重要的作用。试卷质量的好坏对考试公平性有直接影响。而题目难度是影响试卷质量的核心因素,因为过于简单或者过于困难的题目都无法很好地支撑学生能力的区分和人才的选拔。可见,题目难度评估是保障考试公平性需要解决的重要问题之一。与此同时,题目难度评估也在智能教育领域中发挥着重要作用,为智能组卷、题目自动生成和个性化习题推荐等多项智能教育领域的核心任务提供有效支撑。鉴于此,本文对近年来题目难度评估相关的研究工作进行了深入调研和分析,以期为相关领域的研究学者提供帮助。
在对题目难度评估的相关研究工作进行深入讨论之前,首先澄清三个术语——题目、试题和习题之间的区别和联系。根据应用领域的不同,题目可以被称为试题(当其应用于考试时)或习题(当其应用于课后练习时)。可见,试题和习题是题目在不同应用场景下的不同表述。因此本文用术语“题目”统一指代术语“试题”和“习题”。
经典测试理论(classical test theory,CTT)将题目难度定义为正确回答该题的学生占总体学生的比率。佟威等人认为基于题目文本获得的题目难度可称为题目的绝对难度。Zhu 等人则认为题目难度是对题目内容复杂性的度量。此外,Teusner 等人认为不同学生对题目的感知难度与学生的知识状态水平密切相关。同时,Gan 等人也认为存在由学生知识状态水平而决定的题目相对难度。上述对于题目难度的理解可归于两种观点:第一种观点认为题目难度是题目本身特性(例如题型和题目内容等)的反映,本文称之为题目的绝对难度;第二种观点则认为题目难度是学生个体知识状态水平的反映,应该通过学生与题目之间的答题交互表现来量化题目难度,本文称之为题目的相对难度。本文将题目难度分为绝对难度和相对难度两方面分别进行讨论。
题目难度评估是当下教育领域的研究热点,虽然近三年来已有5 篇综述类论文对题目难度评估的相关研究工作进行了分析总结,然而本文和这些论文具有显著区别并作出了新的贡献。其中,文献[16-18]一方面只针对经典的知识追踪模型进行了介绍和分析,没有讨论题目难度评估的其他模型方法;另一方面,没有覆盖近两年最新发表的众多知识追踪模型。文献[19]仅对题目绝对难度的研究方法进行了分析,没有涉及对题目相对难度研究方法的总结。文献[20]则主要分析了基于深度学习方法的知识追踪模型,没有讨论除深度学习方法之外的知识追踪模型。综上,已有的综述类论文要么只关注于题目绝对难度评估相关的研究工作,要么只是针对题目相对难度评估所涉及的知识追踪模型进行了分析总结,均没有以整个题目难度评估领域为视角对近年来的研究进展进行系统的梳理、对比和分析。本文不但系统总结了题目难度评估领域的最新研究进展,还基于同一个公开数据集对近年来最受关注的基于深度学习的题目相对难度评估方法中的典型模型进行了实验对比和分析,从而让读者对这些模型有深入的理解。
本文以整个题目难度评估领域为视角,分析总结了该领域的研究现状,主要贡献包括:
(1)对近十年来题目难度评估的相关研究工作进行了统计、比较和分类;
(2)以题目绝对难度预测和题目相对难度预测为分类框架对相关研究工作进行了分类讨论;
(3)对近年来最受关注的基于深度学习的题目相对难度评估模型进行了实验对比和分析;
(4)对题目难度预测的相关数据集、题目难度预测方法中典型的信息提取方法、模型的评价指标和训练标签进行了系统总结。
1 题目难度评估方法总结与分类
1.1 题目绝对难度评估方法
传统教育中的题目绝对难度评估方法包括预测试和专家评估。预测试是指在题目未被应用到考试前组织一部分学生对所有的题目进行提前测试,再根据学生在测试中的答题表现统计每道题目的难度。预测试方法常被应用于雅思、托福等考试中。易知,预测试法的局限性:(1)其得到的题目难度与参加预测试的学生的知识能力水平紧密相关;(2)存在题目泄露的风险;(3)参与预测试的学生规模一般要求比较大,导致较多人力和财力的消耗。专家评估则由命题经验丰富的领域专家或教师对题目难度进行评估。由于专家或教师的评估结果带有主观性,这无疑会影响题目难度评估的稳定性。
在教育心理学领域,经典测试理论也以学生的测试结果作为题目难度的评估依据。然而,由于该理论存在假设性强且某些参数在理论上具有意义却很难在实际中计算得到等问题,在经典测试理论的运用中通常只是简单以题目得分率或通过率作为题目难度的取值。
鉴于目前已有不少题目绝对难度的评估方法被提出,一些文献对这些题目绝对难度评估方法进行分类。其中,以文献[19]的分类策略最为细致全面。文献[19]将题目绝对难度评估方法分为认知法和系统方法。首先,认知法认为题目的绝对难度是学生正确回答该题所需要的认知能力,进一步可分为启发式法和教育分类法。启发式法又被称为专家评估法,其依赖于领域专家对题目难度进行评估和确定;教育分类法则利用认知模型(例如Bloom 分类模型)评估题目的绝对难度。题目绝对难度评估方法的另一大分支系统方法利用各种计算机技术(例如自然语言处理技术)来量化题目绝对难度,以减少难度量化过程中的人为干预,又可分为统计法和数据驱动法。以经典测试理论为代表的统计法以学生们的历史答题数据为输入并利用统计模型量化得到题目绝对难度值。系统法中的数据驱动法可进一步分为基于规则的方法和基于机器学习的方法。其中,基于规则的方法利用专家制定的规则来计算题目的绝对难度。基于机器学习的方法则是以题目的题干、选项等信息作为题目特征,以题目已知的难度信息作为标签进而利用机器学习模型构建题目绝对难度预测模型,是目前题目绝对难度评估的主流方法。经过统计分析,本文在文献[19]提出的题目绝对难度方法分类策略的基础上进一步将基于机器学习方法细分为基于传统机器学习的方法和基于深度学习的方法。图1 展示了本文的分类策略。鉴于基于机器学习方法是当今题目绝对难度评估的主流技术,本文将在第2 章详细讨论其研究现状。

图1 题目绝对难度评估的方法分类Fig.1 Classification of approaches for question absolute difficulty evaluation
1.2 题目相对难度评估方法
教育心理学领域提出的认知诊断理论是近年来解决题目相对难度评估问题的主流方法。认知诊断是对个体认知过程、加工技能或知识结构的诊断评估。在被运用于题目难度评估时,认知诊断首先以学生答题数据为输入对该生的知识状态水平进行诊断,之后基于诊断结果评估某道题目对于该生的相对难度。认知诊断被分为静态认知诊断(忽略时间因素)和动态认知诊断(考虑时间因素对学生知识状态水平的诊断结果的影响)。
静态认知诊断假设学生的知识状态水平在一定时间内是固定不变的,其利用学生的答题数据对学生的知识状态水平进行评估,进而评估题目对学生的相对难度。作为静态认知诊断模型的代表,项目反应模型(item response model,IRM)和DINA 模型(deterministic input,noisy“and”gate model)都常被用于量化题目的相对难度。其中,项目反应模型首先基于学生的答题结果计算学生的能力参数和题目的特性参数(包括绝对难度、区分度、猜测度),再以这些参数作为Logistics 函数的输入来得到题目对于学生的相对难度信息。项目反应模型没有引入知识点的概念,只将学生的知识状态水平粗粒度地描述为单一的能力值。与项目反应模型不同的是,DINA 模型引入了知识点的概念并通过定义矩阵来描述题目和知识点之间的关系,之后以矩阵和记录了全体学生的答题结果数据的矩阵为输入,并定义相应的项目反应函数来诊断得到学生对各个知识点的掌握程度值,题目对于学生的相对难度值则等于该学生对该题考查的各个知识点的掌握程度值的乘积。近年来,学者们将模糊集理论、机器学习模型与各种认知诊断模型相结合,提出了多种混合认知诊断技术,进一步提高了认知诊断的准确率,因此本文将静态认知诊断方法分为传统认知诊断和混合认知诊断。
动态认知诊断则基于学生的答题数据序列动态评估和更新学生的知识状态水平,以跟踪学生随时间的变化对知识点的掌握情况,进而在不同时刻更新题目对于学生的相对难度信息。由于知识追踪技术利用学生的答题序列追踪学生随时间变化的知识状态水平,从而评估某一道题目对于学生的相对难度,因此有学者认为知识追踪等同于动态认知诊断。根据追踪手段的不同,动态认知诊断方法可进一步分为基于贝叶斯网络的动态认知诊断和基于深度学习的动态认知诊断。
图2 给出了本文对于题目相对难度评估方法的分类策略。由于近十年发表的静态认知诊断相关的文献大都采用了混合认知诊断策略,本文将会在第3.1 节详细介绍这类方法。3.2 节则对动态认知诊断技术进行阐释和分析。

图2 题目相对难度评估的方法分类Fig.2 Classification of approaches for question relative difficulty evaluation
2 题目绝对难度评估
鉴于预测试和专家评估等题目绝对难度评估方法具有耗时耗力、主观性较强、效率低下等缺点,学者们开始通过建立难度预测模型来评估题目的绝对难度。近十年来的题目绝对难度评估方法主要利用机器学习模型评估(或称预测)题目的绝对难度,预测过程可分为四个基本任务:(1)获取题目真实绝对难度;(2)数据预处理;(3)特征提取;(4)题目绝对难度预测模型选择。本文根据题目绝对难度预测方法在特征提取和预测模型选择阶段是否使用深度学习技术将基于机器学习的方法细分为基于传统机器学习方法和基于深度学习方法。题目绝对难度预测方法的分类策略详见图3所示。下文分别对每类方法进行深入讨论。
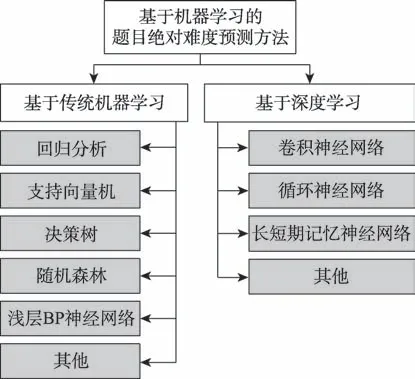
图3 基于机器学习的题目绝对难度预测方法分类Fig.3 Classification of machine learning based approaches for question absolute difficulty prediction
2.1 基于传统机器学习的题目绝对难度评估方法
该类方法利用传统机器学习中的支持向量机、决策树、随机森林、浅层BP(back propagation)神经网络等模型实现对题目绝对难度的预测。
文献[41]基于浅层BP 神经网络提出了一种针对中文阅读理解题的题目绝对难度预测的方法。该方法首先从题目和阅读文本中提取多个特征(例如题干长度、选项长度),其次分析这些特征与题目绝对难度之间的相关性,最终筛选出对题目绝对难度有较高影响力的特征作为BP 神经网络的输入,最终实现对阅读理解题的绝对难度值的预测。
文献[42]则利用支持向量机对台湾社会课程的单选题进行绝对难度预测。首先,使用社会课程教科书和词嵌入技术构建一个语义空间,并将题目元素(包括题目题干、正确答案、干扰选项)投影到语义空间中,以获得相应表征向量。通过计算题目元素表征向量之间的余弦相似性从而得到题目的语义特征。最后,将语义特征输入支持向量机中进行训练和测试,最终实现题目绝对难度预测。
文献[43]利用随机森林模型对汉语选择题进行难度等级预测。首先以汉语教材中的专有名词为基础建立知识树模型,其后将知识树的属性(例如知识树的广度和深度)作为随机森林模型的输入,从而对题目的绝对难度进行等级评估。
文献[44]利用题目编号、题目难度类型、题目总提交次数、题目总通过次数、题目首次提交通过的次数和首次提交通过的总用时作为决策树模型的输入特征,实现了编程题的绝对难度预测。
各种回归模型也常被用于预测题目的绝对难度。例如,文献[45]首先分析得到了英国小学科学测试题目的难度影响因素,具体包括课程变量(涉及课程主题、课程子主题、概念)、题目类型、刺激性质(即题目中的图表类型)、知识深度和语言变量,并使用上述变量建立回归模型来预测题目的绝对难度。又如文献[46]讨论了英语时态的提示性填空题(cued gap-filling items)的难度预测问题。其针对题目文本、填空词语等多个影响题目难度的题目特征进行了岭回归分析,从而建立题目特征与题目难度之间的关系模型。文献[21]则提出从题目文本提取题目的语料库特征(例如词汇特征和句法特征),并将这些特征作为多元线性回归模型的输入来训练该模型从而实现题目绝对难度预测。
上述提及的文献均只选用单一的机器学习模型对题目难度进行预测,而部分论文会利用多种机器学习模型进行题目绝对难度预测,再从中选择特定应用场景下最优的模型。例如,文献[47-48]均是利用多元线性回归和决策树模型对英语阅读理解题中的选择题进行难度预测。又如文献[49]从英文听力题的听力材料文本和题目文本中提取多个特征并基于这些特征训练线性回归、决策树、支持向量机等机器学习模型。文献[50]选取了医学单选题的多个特征(例如语言学特征和信息检索特征),并利用随机森林、线性回归、支持向量机等机器学习模型对题目绝对难度进行评估。文献[51]使用逻辑回归、支持向量机和随机森林对文本信息较为丰富的英语阅读题进行题目绝对难度等级的预测。文献[52]将从选择题的题目文本中提取的可读性特征、语言学特征和信息检索特征作为随机森林、决策树、支持向量机、线性回归模型的输入,实现对题目绝对难度的预测。文献[25]提取题目文本的词频逆文本频率指数特征作为随机森林、决策树、支持向量机和线性回归模型的输入,模型输出题目的绝对难度值和区分度。文献[53]则使用支持向量机、决策树、朴素贝叶斯网络和浅层BP 神经网络对题目绝对难度进行等级评估。
基于传统机器学习的题目难度预测方法的相关文献较多,表1 总结了常用于题目绝对难度预测的传统机器学习模型和相关文献。
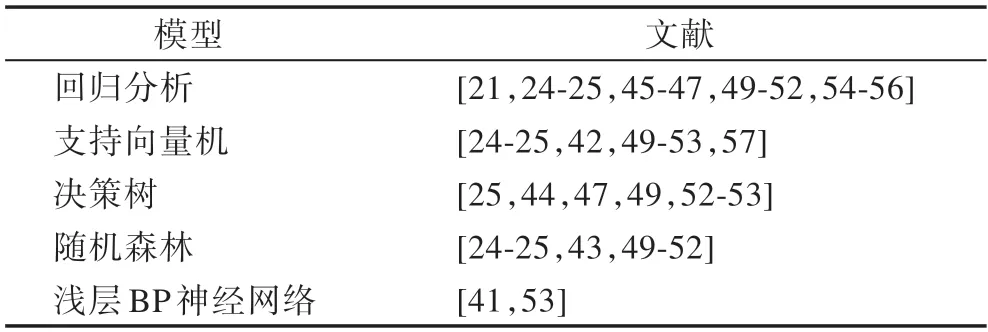
表1 题目绝对难度预测常用的机器学习模型Table1 Frequently-used machine learning models for question absolute difficulty prediction
2.2 基于深度学习的题目绝对难度评估方法
近年来,深度学习技术的运用进一步提升了许多应用领域中预测或分类任务的精度。因此,不少学者也开始利用深度学习框架来提高对题目绝对难度预测的准确性。
文献[58]基于卷积神经网络(convolutional neural networks,CNN)提出了一种预测英语考试中阅读理解题绝对难度的神经网络模型TACNN(test-aware attentionbased convolutional neural network),如图4(a)所示。首先输入层将题目文本进行向量化,其次利用CNN学习题目文本信息(包括阅读文本、题干和选项)的有效语义表征。然后,使用注意力机制来限定阅读文本中每个句子对题目绝对难度评估的贡献。最后,考虑到不同测试中题目难度的不可比性,提出了一种基于考试上下文信息的训练方式来训练神经网络模型TACNN。
文献[12]则基于卷积神经网络和循环神经网络(recurrent neural network,RNN)的思想提出了三种针对数学试题的绝对难度预测神经模型,包括C-MIDP(基于CNN 构建)、R-MIDP(基于RNN 构建)和HMIDP(基于CNN 和RNN 构建的混合模型)。这三种模型的框架如图4(b)所示。具体的,CNN 用来提取题目文本的语义信息,RNN 则用来提取题目文本的序列语义和逻辑信息,此外考虑到不同考试中学生群体的不可比性,在训练模型的过程中同样采用了一种基于考试上下文信息的训练方式,以期提升预测的准确度。
鉴于长短期记忆网络(long short-term memory,LSTM)在处理序列数据上表现良好,文献[23]基于LSTM 网络提出了一种针对汉语阅读理解题的题目绝对难度预测模型,本文将其命名为TCN-DPN(text correlation network and difficulty prediction network),其模型如图4(c)所示。该模型首先将题目文本进行向量化;然后,将题目文本向量输入LSTM 模型中得到题目信息向量,最后题目信息向量经过全连接层输出题目的绝对难度等级。
文献[22]基于深度神经网络模型提出了针对医学考试中选择题的题目绝对难度预测模型DAN(document enhanced attention based neural network),详见图4(d)所示。DAN 首先通过拼接题目的题干和选项构造查询,然后基于查询从一个医学文档数据库中获取和该题相关的医学文档。之后,利用Bi-LSTM(bidirectional long short-term memory)模型构建选择题文本组成部分(即题干、选项和检索到的相关医学文档)的语义特征表达。最后,基于语义特征表达将题目的难度信息分为刻画学习者排除干扰选项困难程度的困惑难度(confusion difficulty)和刻画从医学文档数据库中获取与该题相关的医学文档的困难程度的召回难度(recall difficulty)两部分,并最终以加权求和方式将这两部分难度整合形成该题的绝对难度值。
文献[2]对带图片的选择题的难度评估问题进行研究,首先基于深度多模态嵌入模型学习题目的文本和图片信息的有效表征,然后提出一个基于贝叶斯推理的题目难度预测框架(Bayesian inference-based exercise difficulty prediction,BEDP)来预测该类型题目的绝对难度。BEDP 模型的框架如图4(e)所示。

图4 基于深度学习的题目绝对难度预测重要模型架构Fig.4 Architecture of important deep learning based question absolute difficulty prediction models
表2 对基于深度学习的题目绝对难度预测模型的优点和局限性进行了对比分析。

表2 基于深度学习的题目绝对难度预测模型对比Table 2 Comparison of deep learning based question absolute difficulty prediction models
2.3 题目绝对难度评估的其他方法
虽然近十年提出的题目绝对难度预测方法大多是基于机器学习模型构建的,仍有学者提出了其他的解决思路。例如,针对人工智能课程中的特定类型的题目,包括将自然语言转化为FOL(first-order logic)的题目和FOL 转化为自然语言句子的题目,学者们提出了基于专家制定规则的题目绝对难度评估策略。具体的,学者们从这类题目的特点出发,利用可获取的题目答案参数(例如量词的数量、隐含符号的数量、不同连接词的数量)和专家制定的规则来预测这类题目的绝对难度等级。还有学者提出可以将题目的不同部分或者不同方面的绝对难度进行相乘或者相加来计算题目的绝对难度。例如,文献[60]首先从题目的题干和选项中获取与绝对难度相关的因素,其次利用定义的公式获得题干的难度值和选项的难度,最后将题干和选项的难度分数进行相乘最终得到题目的绝对难度值。文献[61]以求和的方法将任务难度、内容难度和刺激难度(指学生在理解和分析题目陈述内容时所面临的困难程度)整合起来作为题目的绝对难度值。文献[62]则研究了Java 编程题的难度评估问题,根据题目的答案获取到多个软件度量指标(例如圈复杂度、平均嵌套块深度)后对每个软件度量指标的取值进行加权求和后作为题目的绝对难度值。此外,部分学者还将神经网络模型与模糊集理论相结合,实现对题目绝对难度的评估。例如,文献[63]对雅思听力题的听力材料和题目文本进行特征提取,随后利用自适应神经模糊推理系统成功量化了雅思听力题的绝对难度。文献[64]则以Tree 数据结构的参数(例如节点数、树的深度)为输入,并同时利用自适应神经模糊推理系统与神经象征模型构建搜索算法题(例如深度优先搜索算法题)的绝对难度预测模型。
2.4 题目绝对难度评估研究现状分析
近十年提出的题目绝对难度预测方法主要包括基于传统机器学习方法和基于深度学习方法。在论文数量方面,前者占题目绝对难度预测相关文献总数的近九成,这很大程度是因为基于深度学习框架来提升题目绝对难度预测的准确性是需要大量题目数据和学生答题数据作为支撑的,而能访问到这样规模数据的研究机构不多。本文对收集到的近十年的题目绝对难度相关文献进行统计后发现:这些方法所服务的学科集中在英语(21%)、计算机(16%)、医学(12%)、语文(7%)和数学(7%);题型方面,针对选择题所提出的方法占比最大(29%),剩下依次是填空题(7%)、听力题(7%)和编程题(5%)。
3 题目相对难度评估
3.1 静态认知诊断之混合认知诊断方法
近十年提出的静态认知诊断方法大都为混合认知诊断方法,即将经典的认知诊断模型与各种机器学习模型、教育理论进行结合,以优化认知诊断过程从而提高对题目相对难度的预测准确率(表3 展示了近年来典型的混合认知诊断方法)。

表3 混合认知诊断Table 3 Hybrid cognitive diagnostic
项目反应理论(item response theory,IRT)是经典的认知诊断方法之一,为分析学生能否答对某道题提供了可解释的参数。然而经典的IRT 模型仅基于学生的答题结果数据预测题目的相对难度值,未利用题目的文本和知识点信息。鉴于此,文献[36]将IRT 模型和深度学习框架相结合提出了一个深层项目反应理论框架(deep item response theory,DIRT)来弥补传统IRT 模型的不足。DIRT 框架包含了三大模块:输入模块、深度诊断模块和预测模块。输入模块使用能力向量来表征学生对各个知识点的掌握程度值,并设计密集嵌入层将题目文本向量和题目知识点向量进行密集化处理。深度诊断模块中,基于输入模块中生成的学生能力向量、题目文本向量和知识点向量来作为深度神经网络模型的输入。最后的预测模块以深度诊断模块得到的学生能力参数、题目区分度和题目绝对难度作为Rasch 模型的输入,利用训练好的模型预测题目相对难度值。文献[37]则将认知诊断和神经网络相结合,提出了一个通用的神经认知诊断框架,命名为NeuralCD(neural cognitive diagnosis)。
部分学者将认知诊断模型和模糊集理论相结合,提出题目相对难度评估的新思路。部分认知诊断模型(例如DINA 模型)只利用学生在客观题上的答题结果数据,无法充分利用主观题的多级评分信息。为了同时利用学生在客观题和主观题上的答题结果数据,文献[38]将模糊集理论和教育假设结合到认知诊断模型DINA 中,提出了模糊认知诊断框架FuzzyCDF(fuzzy cognitive diagnosis framework)。
近年来,学者们还将矩阵分解技术(matrix factorization,MF)应用到认知诊断领域,即将学生得分矩阵分解为学生潜在矩阵和题目潜在矩阵,分别用以刻画学生和题目在低维空间中的表现程度。基于学生和题目的低维矩阵的乘积对学生得分矩阵进行逼近,进而得到题目对于学生的相对难度。概率矩阵分解(probabilistic matrix factorization,PMF)是常用的矩阵分解方法之一,文献[8]混合运用了PMF 模型和认知诊断模型用于预测学生关于某道题的相对难度。首先将学生答题历史矩阵和专家标注的矩阵作为DINA 模型的输入,得到学生的知识点掌握程度。在得到学生知识点掌握程度后,将其作为先验参数应用于概率矩阵分解中,进而预测题目相对难度。
3.2 动态认知诊断
为了便于读者的理解,本节用知识追踪代替动态认知诊断。由于本文收集到的题目相对难度预测方法大部分是知识追踪相关的,本文根据统计的实际情况将题目相对难度预测方法中的知识追踪分为基于贝叶斯方法和基于深度学习方法,如图5 所示。
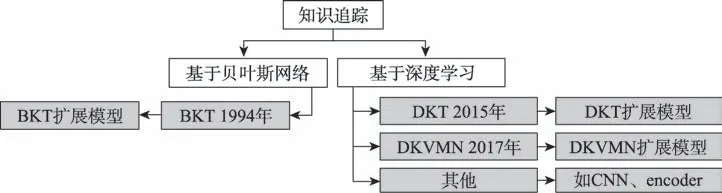
图5 知识追踪方法的分类Fig.5 Classification of knowledge tracking approaches
基于隐马尔可夫模型设计的贝叶斯知识追踪模型(Bayesian knowledge tracing,BKT)是早期知识追踪方法的代表。BKT 将学生对于某个知识点的掌握状态建模为一个二值变量,包括掌握和未掌握两个状态,并假设该生对于每个知识点都有四个参数:(1)先验知识水平,即该生未答题前对该知识点的掌握程度;(2)学习率,指该生每次答题后知识点从未掌握状态转移至掌握状态的概率;(3)猜测概率,指该生未掌握该知识点但猜测答对其对应题目的概率;(4)失误概率,指该生掌握该知识点却失误答错其对应题目的概率。EM(expectation maximum)算法常被用来估计BKT 模型中的以上四个参数,利用得到的参数并通过隐马尔可夫模型更新学生知识点的掌握状态。
在BKT 模型的基础上:一方面,一些学者继续从学生方面和题目方面探讨其他因素(如学生遗忘行为、学生不同的学习能力、题目绝对难度、知识点的层次结构关系)对题目相对难度的影响;另一方面,也有学者利用教育心理学领域的理论模型扩展BKT模型以获得更高的题目相对难度预测准确率。表4总结比较了近十年提出的BKT 扩展模型。

表4 BKT 扩展模型Table 4 Extended models for BKT
在扩展BKT 模型的研究任务中,部分学者考虑加入学生方面的多种因素以提升对学生知识状态水平的评估准确度,继而提高对题目相对难度的预测精度。例如,文献[72]假设学生间隔一段时间后的答题表现下降的原因有二:(1)学生遗忘知识点内容;(2)学生答题失误。利用该假设,分别将学生遗忘概率和同一天的失误概率作为参数引入到BKT 模型。文献[39]从学生的个性化特性出发提出了三种改进的BKT 模型,分别考虑不同学生对知识点的初始掌握程度、不同学生对知识点的学习速率以及同时考虑了以上二者。文献[75]将利用便携式脑电图设备检测学生的心理状态数据嵌入到BKT 模型中。文献[80]则基于所收集的学生答题行为特征对BKT 模型进行了扩展改进。文献[82]则直接加入了表征学生情感状态的变量(如是否困惑、无聊等状态)来扩展标准的BKT 模型。文献[84]提出了四个改进的BKT模型:BKT+F(考虑遗忘因素)、BKT+S(考虑知识点间的相似性)、BKT+A(假设能力较强的学生有较低的失误率和较高的猜测概率)以及BKT+FSA(前三个模型的综合)。
标准BKT 模型将学生对知识点的掌握状态设置为掌握和未掌握两个状态。文献[86]提出学生对知识点的掌握状态不应只是一个二值变量,继而在标准的BKT 模型中增加了一个从未掌握到掌握的过渡状态。而文献[81]在学生对知识点的掌握和未掌握两个状态之间添加两个中间状态对标准BKT 模型进行扩充。文献[88]则提出了一个多状态BKT 模型,将描述学生对知识点的掌握状态的变量从标准BKT 模型中的两种状态(即“掌握”和“未掌握”)扩展到21种状态。
此外,还有部分学者考虑加入题目方面的多种因素来提升BKT 模型对题目相对难度的预测效果。例如,文献[74]考虑了学生当前正在回答的题目与之前已回答的题目之间的相似性,并利用题目间的相似性来改进BKT 的预测效果。在看到标准BKT 模型缺乏对学习领域中不同知识点间层次关系的描述能力,文献[77]提出了能够表征和利用知识点拓扑结构关系的动态贝叶斯网络。文献[73]则引入题目绝对难度特征来改进标准的BKT 模型。
上述研究工作表明将学生方面的多种因素或题目方面的多种因素融合到标准BKT 模型中均可有效提升模型的预测准确率。鉴于此,有学者同时利用学生方面和题目方面的多种因素对标准BKT 模型进行扩展。例如,文献[79]提出一个BKT改进模型Fast,允许将学生方面和题目方面的一般特征集成到该模型中。又如,文献[83]利用教学系统中课程章节学习视频之间的结构信息设计了两种知识跟踪方法:Multi-Grained-BKT 和Historical-BKT。其中,前者考虑了粗粒度知识点(例如Python 数据类型)和细粒度知识点(例如字符串、List 列表)之间的关联结构关系,后者则设定学生猜测答对和失误答错的概率都取决于其上一次的答题结果,即如果上一次答题是正确的,则此次答题猜测答对的概率越大而失误概率越小。
除了引入学生和题目方面的影响因素,还有学者或将其他理论或技术与标准BKT 模型相结合,或考虑将其他方面的特征融入到标准BKT 模型中,以提升BKT 模型对题目相对难度信息的预测性能。例如,文献[76]将潜在因子模型和BKT 模型相结合。文献[78]则将BKT 模型和项目反应理论模型(即IRM)进行整合。又如文献[85]考虑不同类型的教学干预会对学生的学生状态产生不同的影响。文献[87]则将时差信息集成到BKT 模型中。
(1)DKT 模型及其扩展模型
BKT 模型一方面需要领域专家事先定义知识点因此引入了一定的主观性,另一方面假设学生对知识点的掌握程度为掌握或未掌握的二元状态过于简化。为了弥补BKT 模型的不足,学者们开始尝试利用近年来流行的深度学习框架设计题目相对难度的预测模型。文献[89]首次利用深度神经网络对学生学习过程进行建模,提出了深度知识追踪模型(deep knowledge tracing,DKT)。
DKT 模型架构图如图6 所示。其以学生每一个时间步(1,2,…,)的历史答题数据序列{,,…,x}为输入,并利用LSTM 的隐藏状态向量{,,…,h}表征学生不同时刻的知识状态水平,进而预测学生在不同时刻正确回答每一道题的概率{,,…,y}(即题目对于学生的相对难度)。

图6 DKT 模型架构Fig.6 Architecture of DKT model
由于DKT 模型无法建模学生对于各个知识点的掌握程度,且隐藏状态向量的可解释性差,DKT 模型的可解释性也不强。除了考虑学生的历史答题数据序列,DKT 模型没有将影响题目绝对难度的学生和题目方面的因素(例如学生的学习率、遗忘因素、题目的文本和绝对难度等)引入模型。针对上述不足,学者们一方面尝试利用项目反应理论和注意力机制等理论或技术对DKT 模型可解释性不强的问题进行优化,另一方面通过向DKT 模型中融入学生或题目方面的影响因素对DKT 模型进行了改进。表5 对DKT 的扩展模型进行了总结和对比。下面对代表性的DKT 扩展模型进行介绍。
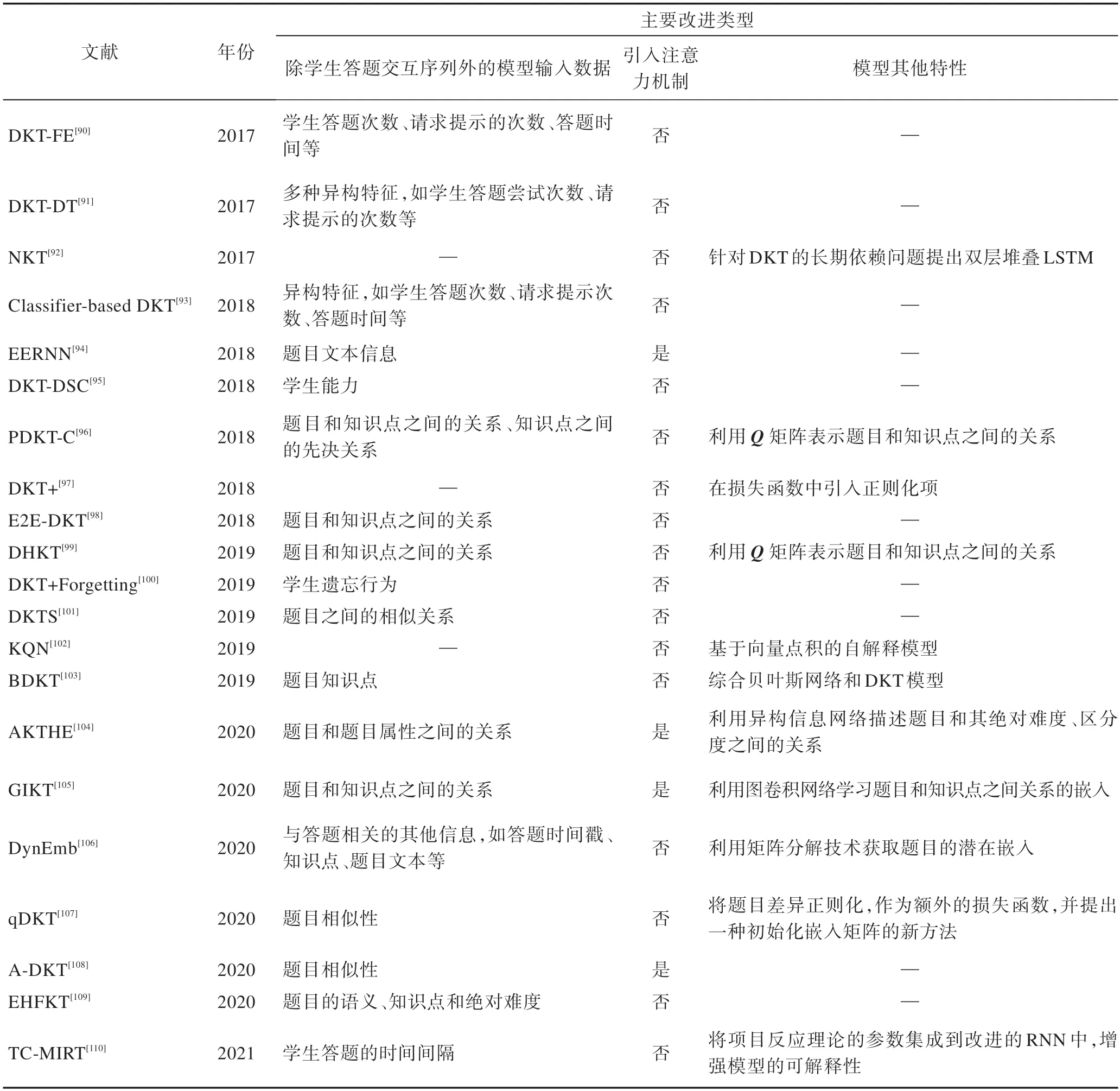
表5 DKT 模型的扩展模型Table 5 Extended models of DKT model
由于DKT 模型的输入仅考虑学生的答题交互序列而忽略了其他学生方面的特征,部分研究工作考虑加入学生方面的多种特征以提升DKT 模型评估学生知识状态水平的准确度。例如,文献[90]利用特征工程将学生方面的丰富特征(例如学生答题次数、请求提示的次数)作为标准DKT 模型的一部分输入,提出了一个新的深度知识追踪模型,本文将其命名为DKT-FE(deep knowledge tracing of rich features)模型。文献[100]则考虑导致学生遗忘行为的两大类因素:学生距离上一次答题的时间和过去对一个题目的答题次数,通过将学生遗忘行为有关的多种特征向量化,然后将向量化后的特征拼接到RNN 模型的输入和输出空间。文献[95]则考虑了不同学生的学习能力的差异性。
此外,一些研究工作考虑加入题目方面的多种特征对DKT 模型进行扩展以提升评估学生知识状态水平的准确度。例如,文献[101]考虑题目所包含知识点之间的相似性关系,将知识点之间的相似性关系转化为题目关系图,其中节点表示题目,边表示两道题之间存在相似性,并将题目关系图向量化后和向量化后的答题序列一起作为模型的输入。文献[107]同样考虑了题目之间的相似性,并提出一种图拉普拉斯正则化方法作为正则化损失函数来扩充原始的损失函数,从而将题目相似度整合到了DKT 模型中。文献[96]则将知识点之间的先决关系整合到DKT 模型中。文献[99]利用了题目和知识点之间的关系,将其和学生答题交互序列一起作为DKT 模型的部分输入。文献[109]则同时将题目方面的知识点、题目语义和题目绝对难度信息和答题序列一起作为DKT 模型的输入。
部分研究工作在利用题目方面的特征来加强知识跟踪方法的有效性之外,还将神经网络中的注意力机制整合到DKT 模型中以期进一步提高模型评估学生知识状态水平的准确率。例如,文献[94]提出了一个能够利用题目的文本信息的深度知识追踪框架,命名为EERNN(exercise-enhanced recurrent neural network)。EERNN 模型需要获得完整的题目文本信息以提取题目之间的相关性,但由于知识产权和隐私保护等原因,通常很难获取到完整的题目文本。为了应对该局限性,文献[108]提出可以基于题目的知识点信息来提取题目之间的相似性继而提出了一种基于注意力机制的深层知识追踪模型。此外,还有文献或利用异构信息网络或基于图卷积神经网络来扩展DKT 模型。
为同时利用学生方面和题目方面的多种特征,文献[91]使用分类与回归树(classification and regression trees,CART)对学生方面和题目方面的特征(例如答题时间、题目文本)进行特征处理。文献[93]拓展了文献[91]的工作,使用其他的分类树模型进行特征处理。
此外,部分研究工作还提出将DKT 模型与BKT模型以及教育心理学领域中的理论模型(例如项目反应模型)进行整合。例如,文献[103]综合了贝叶斯神经网络与DKT 模型,不仅可以对学生与题目的交互行为进行建模,还有效地防止过拟合,提高了模型的泛化能力。文献[110]则将多维项目反应理论的参数集成到一个改进的RNN 模型中。
DKT 的扩展模型除了上述提及的考虑学生方面、题目方面或者同时考虑上述两方面的丰富特征外,还有部分研究工作或对DKT 模型的损失函数进行优化,或利用机器学习技术对DKT 进行扩展。例如,文献[97]利用数据可视化技术发现DKT 模型存在的两个问题:第一是DKT 模型无法重构输入信息(即学生在某道题上回答错误,与该题相关的知识点的掌握程度却在上升);第二是DKT 模型所预测的学生对知识点的掌握程度并不是随着时间的推移逐渐过渡变化的。因此,作者提出了DKT+模型用于解决上述问题,定义了“重构错误”(reconstruction error)和“波动准则”(waviness measures)作为正则化损失函数来扩充原始的DKT 模型中的损失函数。文献[98]则将题目与知识点之间的关系看作一个二元嵌入矩阵,提出了一个用于学习该矩阵的模型,然后将学习到的嵌入矩阵应用于DKT 模型的输入空间中,并对模型的损失函数进行了改进。DKT 的扩展模型还有很多,在此不一一赘述,感兴趣的读者可参看表5 给出的信息。
(2)DKVMN 模型及其扩展模型
DKT 模型将学生对所有知识点的掌握程度都归纳为一个隐藏状态,导致DKT无法输出学生对于具体知识点的掌握程度情况,因而模型的可解释性较差。鉴于此,文献[111]利用记忆增强神经网络(memoryaugmented neural networks,MANN)的思想提出了动态键值记忆网络(dynamic key-value memory networks,DKVMN)模型。


表6 DKVMN 模型的扩展模型Table 6 Extended models of DKVMN model

图7 DKVMN 模型架构Fig.7 Architecture of DKVMN model
部分学者提出可以将更多能捕获的学生方面的特征加入标准的DKVMN 模型对其进行扩展,以期提高预测准确率。例如,以DKVMN 模型的基本框架作为出发点,文献[113]将学生申请答题提示的行为数据也作为模型输入的一部分,并将预测学生在接下来的答题阶段是否申请答题提示作为知识追踪的子任务,从而提出了一个多任务知识追踪模型。又如,文献[118]将学生丰富的答题行为特征(例如学生回答某道题的尝试次数、学生答题的响应时间)和学生答题交互序列一起作为模型的输入。文献[40]则考虑了影响学生知识遗忘问题的四个因素:学生重复学习知识点的间隔时间、重复学习知识点的次数、顺序学习的间隔时间以及学生对知识点的掌握程度。
部分学者提出可以同时利用学生方面和题目方面的丰富特征优化DKVMN 模型。例如,文献[117]一方面将题目绝对难度信息、学生所处的学习阶段(例如预习阶段、上课阶段、家庭作业阶段)和答题时间信息作为模型的输入,另一方面引入题目与其涉及的知识点之间的关系权重。
此外,不少学者将DKVMN 模型与各种模型进行结合。例如,针对DKT 模型可解释性差的问题,文献[119]综合具有一定可解释性的DKVMN 模型和可解释性较强的IRT 模型提出了一种新颖的深度知识追踪模型Deep-IRT。Deep-IRT 模型使用DKVMN 模型对学生和题目间的交互进行建模,从而得到题目绝对难度值和学生的能力值,随后输入IRT 模型以估计题目相对难度。文献[115]在DKVMN 模型和DKTDSC 模型(一种改进的DKT 模型)的基础上提出了一个命名为DSCMN 的知识追踪模型。该模型通过所捕捉的学生长期学习过程中的每个时间间隔内的学习能力信息来优化现有的知识追踪方法。文献[114]则整合了DKVMN 模型和EERNN 模型(一种改进的DKT 模型)提出了知识追踪模型EKT。该模型使用双向LSTM 提取题目文本的语义特征,并将该特征与学生答题交互序列组合作为模型的输入。文献[116]则综合了DKT 模型的循环建模能力和DKVMN 的记忆能力,提出了新的深度知识追踪模型。在意识到对于给定的一道题并非所有的学生答题数据都有助于预测该题的相对难度,文献[116]因此通过在DKVMN模型中引入一个Hop-LSTM 模型,从而使得新模型能够跳过答题序列中与目标题目不相关的题目,继而获得更高效、准确的模型预测性能。
(3)基于Transformers的模型
部分学者将自然语言处理领域的Transformers 模型应用在知识追踪领域。文献[121]首次基于Transformers模型的简化版对学生答题交互序列进行建模,继而提出了一种完全基于注意力机制的知识追踪模型SAKT(self-attentive knowledge tracing)。SAKT 模型的架构图如图8 所示。图中,SAKT 模型首先对输入的学生答题历史交互序列{,,…,x}进行嵌入编码;然后利用位置编码机制对序列的位置进行编码;其后的多头注意力机制旨在确定学生当前作答题目与其历史作答题目之间的相关性;在经过一个前馈神经网络后,模型的预测层使用全连接网络来预测题目对于学生的相对难度值。

图8 SAKT 模型架构Fig.8 Architecture of SAKT model
SAKT 模型被提出之后,文献[122]提出分别使用不同的多头注意力机制层对学生答题交互序列中的题目序列和答题结果序列分别进行处理,并将处理得到的结果作为另一个多头注意力机制层的输入,以期更好地捕获题目和答题结果间的复杂关系。文献[123]则改进了Transformers 模型的结构,使得改进后的模型(本文将其命名为DKTT 模型)不但能够自动识别题目涉及的知识点,还可以处理学生答题交互序列的时间戳。表7 总结了各个基于Transformers的知识追踪模型的优点和局限性。

表7 基于Transformers的知识追踪模型总结Table 7 Summary of knowledge tracking models based on Transformers
(4)其他的深度学习模型
除了运用LSTM、RNN、MANN 和Transformers模型对学生的答题交互序列进行建模,部分学者还尝试运用深度学习中的其他模型建模学生的答题交互序列。例如,文献[124]提出了一种基于图神经网络的知识跟踪模型GKT(如图9 所示),通过将题目知识点间的关系转换为图,进而将题目相对难度预测任务转化为图神经网络中的随时间变化的节点分类任务。文献[125]考虑了学生的个性化特性(如不同学生具有不同的先验知识和学习率),并利用卷积神经网络模型实现题目相对难度的预测,其模型框架CKT如图10 所示。还有学者提出了基于其他深度学习框架的题目相对难度预测模型,涉及联邦学习、可微神经计算机和推荐领域中的DeepFM模型。

图9 GKT 模型架构Fig.9 Architecture of GKT model

图10 CKT 模型架构Fig.10 Architecture of CKT model
(5)基于深度学习的知识追踪模型的对比
深度知识追踪模型是当下题目相对难度评估领域的研究热点,因此本小节首先分析对比了当下典型的深度知识追踪模型,包括DKT、DKVMN、SAKT、GKT和CKT,详见表8 所示。

表8 DKT、DKVMN、SAKT、GKT 和CKT 模型对比Table 8 Comparison of DKT,DKVMN,SAKT,GKT and CKT model
为了帮助读者加深对已有深度知识追踪模型的理解,现对目前代码已开源的DKT、DKVMN、GKT和CKT 模型进行实验比较和分析。虽然提出这几个模型的文献都给出了各自模型基于ASSISTments2009(https://sites.google.com/site/assistmentsdata/home/assistment-2009-2010-data/skill-builder-data-2009-2010)这个公开数据集得到的实验数据。然而,这些文献中给出的实验数据仍不能作为横向比较这些模型的依据,原因如下:(1)不同文献所使用的ASSISTments2009数据集版本可能存在差异,因为ASSISTments2009 数据集版本曾被多次更新。(2)即使所采用的ASSISTments2009 数据集的版本相同,不同文献对数据集的预处理方法也不相同(例如提出DKVMN 模型的文献[111]与提出GKT 模型的文献[124]中的数据预处理方法不相同)。(3)即使数据集的预处理结果相同,部分文献在比较现有模型时所设置的现有模型的参数并非其最优设置(例如DKVMN 模型的来源文献[111]和CKT 模型的来源文献[125]中虽然数据预处理后得到的数据一样,但前者的实验结论是DKVMN比DKT 优异,后者的实验结论却是DKT 比DKVMN优异,由此可推断上述两篇文献并未同时使用各个模型的最优参数进行实验)。鉴于此,本文基于能满足所有待比较模型数据需求的ASSISTments2009 数据集,统一使用文献[131]给出的数据集预处理方法,并在模型参数设置方面遵循提出各个模型的文献中推荐的参数设置,横向比较了DKT、DKVMN、GKT和CKT 这四种深度知识追踪模型完成题目相对难度评估任务的AUC 值(area under curve,AUC)和模型的训练时间。实验中将模型训练阶段的参数epoch 和batch_size 分别设置为100 和32。实验所用的硬件环境为8核CPU,64 GB内存,1.5 TB硬盘;软件环境为64位Ubuntu 20.04 操作系统,模型实现语言为Python 3。此外,ASSISTments2009 数据集预处理后所得到的数据集的基本情况如下:学生数量为3 841,知识点数量为123,学生答题记录数目为283 103。
表9 给出了ASSISTments2009 数据集上各个模型的AUC 值和模型的训练时间。观察表9 可得到如下结论:
(1)DKVMN 模型和CKT 模型的题目相对难度评估准确性优于DKT 模型。作为首个被提出的深度知识追踪模型,DKT 模型用一个维度固定的隐藏向量表示学生对任意多个知识点的掌握程度,因此隐藏向量的表达能力受限,导致DKT 模型的评估准确性低于DKVMN 模型和CKT 模型。与DKT 模型不同,DKVMN 模型为每个潜在知识点单独定义了一个状态向量,获得了较大的外部存储能力,不但增强了模型的可解释性,还有效提高了模型的评估准确性。表9 还展示出CKT 模型略优于DKVMN 模型,得益于其在建模时考虑了学生个性化的先验知识和学习率。此外,基于CNN 构建的CKT 模型在实验中取得了最优的评估性能也说明了CNN 模型适用于对知识追踪问题进行建模。

表9 重要深度知识追踪模型实验对比Table 9 Experimental comparison of important deep knowledge tracking models
(2)ASSISTments2009 数据集上GKT 模型的题目相对难度评估准确性最低。这是因为GKT 模型的预测精度受学生历史答题交互序列长度的影响:序列长度较长时(GKT 模型原文实验使用的数据集的序列长度限制为不小于10),其模型预测性能优于DKVMN 模型;而当序列长度较短时(本文实验使用的数据集的序列长度限制只为不小于3),其模型预测性能则显著低于DKVMN 模型。可见,GKT 模型对学生历史答题交互序列较长的数据集更为友好,更能发挥其优越性。
(3)CKT 模型的模型训练时间最短,GKT 模型的训练时间最长。这是因为CKT 模型使用CNN 模型对学生答题交互序列进行建模,所以与其他模型相比需要最少的模型训练时间。GKT 模型由于引入了图结构,在追踪学生的知识状态变化时,需要执行基于图结构的推演计算,导致其模型的训练时间显著高于其他模型。
近十年提出的题目相对难度预测方法主要利用动态认知诊断中贝叶斯网络方法和基于深度学习方法构建,但仍有学者提出了其他的解决思路。例如,为了对学习过程的动态因素进行建模,文献[130]引入时间维度,将二维空间的矩阵分解扩展至三维空间的张量分解从而更好地实现对题目相对难度信息的预测。为了考虑时间因素,文献[66]将学生的答题得分记录表示为学生得分张量,并将记忆和遗忘曲线综合到概率矩阵分解模型中提出了KPT(knowledge proficiency tracing)模型。为了解决某些学生答题数据较稀疏的问题,文献[132]在KPT 模型的基础上考虑了题目之间的关系并提出了EKPT(exercisecorrelated knowledge proficiency tracing)模型。文献[133]则利用回归模型对题目相对难度进行预测,并利用因子分解机解决特征组合问题,提出了知识追踪模型(knowledge tracing machines,KTM)。KTM模型并不考虑学生答题过程中的时间因素,属于静态认知诊断模型。为此,文献[15]在KTM 模型的基础上考虑了学生随着时间变化的学习率、遗忘等因素提出了一个动态的知识追踪模型。
3.3 题目相对难度评估研究现状分析
本节将收集到的近十年的题目相对难度预测相关文献进行整理分析后分为两类:一类是静态认知诊断(论文占比约7%);另一类是动态认知诊断(论文占比约93%)。可见,动态认知诊断相关的论文更为丰富,可被进一步分为基于贝叶斯网络方法(论文占比约26%)、基于深度学习方法(论文占比约68%)和其他方法的动态认知诊断(论文占比约6%)。由统计的数据可知基于深度学习的方法是目前题目相对难度预测的主流方法。
4 数据集、评价指标和题目真实难度标签
本章对题目难度预测相关的数据集、题目难度预测模型常用的评价指标、训练模型所用的题目真实难度标签来源以及深度题目难度预测模型中典型的信息提取方法进行介绍和总结。
4.1 数据集
题目的绝对难度通常是以题目本身的属性为出发点实现评估量化的。不同学科的题目在题型和内容上均有所区别,导致对不同学科的题目所提取的特征存在较大差异。鉴于此,题目绝对难度评估方面的研究工作一般都是针对特定学科的特定题型进行讨论的。因此是否拥有相应学科和题型的数据集以及所拥有的数据集是否具备一定规模决定了研究是否能顺利进行以及某些模型方法是否能够得以运用。目前,题目绝对难度评估研究领域的相关文献所使用的较大规模的题目数据集大都来自大型公司,往往是不开源的。例如文献[58]所用的英语阅读理解题数据集和文献[12]所用的数学题数据集均来自科大讯飞股份有限公司;文献[2]所用的两个数据集(分别对应带图片的数学选择题和医学选择题)来自视源(CVTE)旗下的希沃(Seewo)公司和希科医疗(Xicco)公司;文献[22]所用的医学题数据集则由腾讯医疗AI 实验室提供。若无法获得公司提供的数据集,学者们则通过自主开发的教学服务平台/系统收集数据或者在课堂上手动收集数据,但是这些方式所收集到的数据集的规模有限。因此,如何获取到高质量、大规模、包含题目数据以及学生答题数据的数据集从而支撑题目绝对难度评估方面的研究仍是一个需要解决的难题。
对于题目的相对难度评估方法而言,认知诊断和知识追踪都是近年来热门的题目相对难度预测方法。标准的认知诊断和知识追踪模型的输入较为简单,即学生的答题交互序列数据,因此对特定的学科和题型不具依赖性。另外某些学者提出利用题目文本信息特征扩展标准的模型以提高预测的准确率,使得其所需要的数据集具有一定的特殊性。
表10 总结了目前开源的、被用于支撑题目相对难度评估研究工作的学生交互序列数据集。

表10 学生交互序列公开数据集Table 10 Public datasets of student interaction sequences
4.2 评价指标
根据模型预测结果的不同,题目绝对难度预测模型分为分类模型和回归模型两种。如果模型预测得到的是题目难度的类别(例如可分为简单、中等和困难三类),则该模型为分类问题。反之,如果题目绝对难度预测模型得到的是一个题目难度的预测值,那么该模型为回归模型。对于题目绝对难度预测的分类模型,其常用的评价指标为准确率(accuracy,ACC),表示模型预测的分类是正确分类的情况占总样本数的百分比,如式(1)所示。题目绝对难度预测的回归模型常用的评价指标有均方根误差(root mean square error,RMSE)和平均绝对误差(mean absolute error,MAE),两者都用于表示模型预测的题目绝对难度值和真实题目难度值之间的差距,具体计算公式分别如式(2)和式(3)所示。

其中,表示题目总数,表示模型预测正确的题目数量,该评价指标值越高越好。



对于题目相对难度的预测模型,也常从回归或者分类的角度对模型的效用进行评估。常用的分类评价指标包括AUC(如式(4)所示)和ACC,常用的回归评价指标则为RMSE 和MAE。
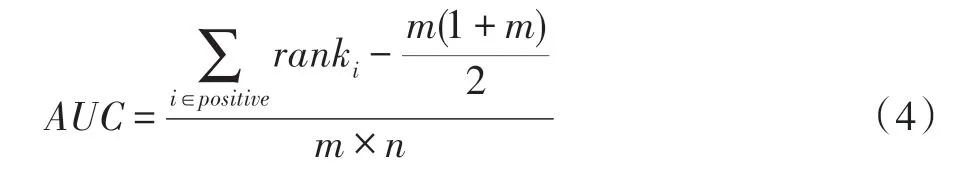
AUC 表示模型预测的正例排在负例前面的概率,其中为正例的数量,为负例的数量。
4.3 题目真实难度标签
题目真实难度作为题目难度预测模型的训练标签,对于训练题目难度预测模型具有重要作用。经统计,如表11 所示,根据题目真实难度标签来源的不同可将题目绝对难度预测模型中的真实难度标签分为两大类:专家评估法和基于学生答题数据统计法。前者需要邀请领域专家(如任课教师、课程助教等)对题目的绝对难度进行评估并给出评估结果。后者以一定规模的学生答题数据为输入并利用统计学公式计算得到题目的真实难度。常用的统计学公式为题目通过率计算公式和项目反应理论涉及的公式。而题目相对难度预测模型则使用学生在题目上的真实答题结果作为训练标签。

表11 题目真实难度标签的来源Table 11 Sources of true difficulty lables of questions
4.4 典型的信息提取方法
为了让读者更加了解题目难度预测的研究思路,现对基于深度学习的题目难度预测模型中典型的信息提取方法进行分析和总结。
题目绝对难度方面,由于题目绝对难度主要基于题目本身的特性得到,近年来,学者们开始利用神经网络模型从题目文本中获取题目绝对难度,该种方法首先利用词向量模型(如word2vec、BERT)对题目文本进行向量化,随后输入神经网络中提取语义信息、逻辑信息等。例如,文献[12]和文献[58]均利用word2vec 技术将题目文本向量化,随后利用神经网络(如CNN、LSTM)提取文本中的语义信息或者逻辑信息。使用神经网络对题目中的信息进行提取,无需手动定义特征和特征提取,但需要大量的题目文本数据和训练标签,因此,该信息提取方法只适用于数据量较大的数据集。
题目相对难度方面,除了利用学生的答题交互序列,部分文献还将题目方面(如题目文本、题目和知识点之间的关系)和学生方面(如学生答题的尝试次数、学生答题的时间间隔)的丰富信息也作为输入。题目方面的信息提取方法主要可以分为两大类:第一类是专家标注,例如,文献[99]中专家手动标注矩阵,从而得到题目和知识点之间的包含关系,文献[96]中专家手动标注矩阵、知识点间先决依赖关系的矩阵,文献[117]中需要专家手动标注题目绝对难度标签。专家标注得到的题目信息准确率较高,但该方法是劳动密集性的,耗时耗力,只适用于学生答题交互序列涉及的题目数据量较少的场景。另一类则利用机器学习的方法对题目方面的信息进行提取。例如,文献[94]设计了一个双向的LSTM 模型,从而可以从题目文本中学习每个题目的语义表示,文献[104]利用异构信息网络对题目和其属性之间的复杂信息进行提取,文献[105]利用图卷积神经网络捕捉题目和知识点之间的高级关系。该类型的信息提取方法能自动提取题目方面信息,无需具备专业知识的人进行标注,可适用于具有大量数据的智能教育线上场景,该类方法除了需要大量的数据集以外,不同的神经网络方法存在差异,例如文献[104]中使用异构信息网络提取题目和题目属性之间的关系,而异构信息网络需要依赖适当的元路径,而元路径的定义需要领域知识且具有一定的主观性。文献[94]需要数据集中包含较为完整的题目文本,而开源的学生交互数据集中鲜少有数据集会提供完整的题目文本。而学生方面的典型信息提取方式可分为两大类:第一类依赖于系统的设计,且占据了学生方面相关的大部分信息(如学生答题的时间间隔、学生获取答题提示),利用系统获得的学生信息准确直观且经过简单处理后可直接作为题目相对难度预测模型的一部分输入,但该类型的信息获取需要专业人员提前进行定义,且依赖于开发人员提前对智能教学系统进行设计,当系统不具备提取特定信息的功能时,无法获得该类型的学生信息。第二类学生方面的信息无法通过系统直接得到,需要综合系统收集的多种学生信息。例如文献[40]中学生的遗忘行为需要综合系统收集到的多个学生方面的信息(包括学生距离上次学习相同知识点的时间间隔、距离上次学习的时间间隔、重复学习知识点的次数和学生原本对于该知识点的掌握程度)。文献[100]合并与遗忘相关的多种类型的学生信息来考虑遗忘。
5 总结和展望
5.1 总结
题目难度评估是教育领域需要解决的重要问题,近年来学者们提出了不少题目难度评估的新方法。本文将题目难度评估分为题目绝对难度评估和题目相对难度评估两部分,并分别进行分析总结。
(1)题目绝对难度评估方面。题目绝对难度评估的主要依据是题目自身的特性。不同学科下的题目特性存在差异,导致大部分题目绝对难度的评估方法的泛化能力有限,甚至只能解决面向特定学科和特定题型的难度评估问题。此外,大部分工作的研究对象集中为题目文本信息较为丰富或者答案唯一的题目,从而便于问题的建模和求解。数据集方面,大部分用于评估题目绝对难度评估模型的数据集是自主收集的且规模不大。由于缺少公开的大规模数据集,近十年发表的基于机器学习的题目绝对难度预测工作大部分是基于传统机器学习方法设计的。近年来一些学者和大公司合作,在大公司提供的较大规模的数据集上利用深度学习框架成功提升了题目绝对难度的预测精度。
(2)题目相对难度评估方面。认知诊断和知识追踪都是近年来学者们用于解决题目相对难度评估的热点方法。尤其是基于深度学习框架设计的知识追踪模型更是成为了题目相对难度评估的主流策略,代表性模型包括DKT 模型、DKVMN 模型和基于Transformers 的知识追踪模型等。标准的DKT 模型和DKVMN 模型的输入较为简单,因此不少学者利用学生方面和题目方面的丰富特征来增强这些模型的输入,从而有效提升了模型预测的准确率。此外,部分学者还尝试利用神经网络中的注意力机制和教育心理学的相关理论来解决深度知识追踪模型的模型可解释性不强的问题。支撑题目相对难度研究的公开数据集资源较为丰富,部分公开数据集的数据规模也比较大,为基于深度学习框架的题目相对难度预测模型的设计和评估提供了保障。
5.2 展望
虽然题目难度评估研究领域近年来有不少研究工作在国内外高水平的会议或期刊上发表,但该研究领域仍存在以下问题亟待解决。
(1)缺乏支撑题目绝对难度评估研究的公开数据集(尤其是大规模数据集)。由于直接发布题目信息(例如题目题干和选项)可能会增加试题泄露的风险,目前鲜有支撑题目绝对难度评估的公开数据集(尤其是大规模的公开数据集)。因此亟待研究题目数据的安全开源方法,从而更好地支撑基于深度学习框架的题目难度预测模型的设计与评估。
(2)题目中提取的信息不够丰富。目前大部分题目绝对难度的评估方法仅针对题目的文本进行语义提取或逻辑提取,而这些题目信息提取策略并不适用于那些文本信息较少的题目,例如编程题和开放式简答题等。因此,除上述提及的题目信息提取角度之外,如何从更多的题目信息提取角度出发,设计面向文本信息较少的题目的信息提取方法也是需要解决的问题。例如英语学科的语法填空题,该类型的题目更侧重于语法结构,因此可考虑提取句子中的语法结构信息。此外,对于具有大量代码的编程题,可考虑从该类型题目的答案(即代码)中提取信息,如将代码转换为抽象语法树,利用卷积神经网络等提取树中提取代码的逻辑结构信息。
(3)需要应用其他深度学习框架进一步提升题目难度评估的准确性。不论是在题目绝对难度评估领域还是题目相对难度评估研究领域,近年研究已表明基于深度学习框架的模型方法能够进一步提升传统机器学习模型的准确性。因此,如何运用更多的深度学习框架(例如生成对抗网络、多任务学习网络等)来改进教育领域的题目难度评估问题也是亟待研究的重要问题。
(4)没有充分利用知识点间的先决依赖关系来提升题目难度评估的准确性。大量研究工作表明,增加题目难度评估模型的输入信息种类能进一步提高现有模型的评估准确性。鉴于题目考查的知识点之间往往存在着先决依赖关系,而现有的题目难度评估模型大都忽略了该信息。例如,数据库的三个知识点“第一范式”、“第二范式”和“第三范式”之间存在先决依赖关系,掌握前面两个知识点是掌握第三个知识点的先决条件。那么易知,在题目绝对难度方面,涉及知识点“第三范式”的题目的绝对难度大于涉及知识点“第二范式”和“第一范式”的题目,而该信息可用于求精题目绝对难度的评估结果。在题目相对难度方面,如果某个学生在知识点“第三范式”的相关题目上表现良好,却在知识点“第一范式”或者“第二范式”的相关题目上表现较差,则意味该学生很可能是猜对了“第三范式”的相关题目,即该题相对于该学生的相对难度评估值应该进行修正。因此,如何利用知识点之间存在的先决依赖信息从而进一步提升现有题目难度评估模型的准确性是需要研究的重要问题。
(5)部分题目相对难度评估模型缺乏教育层面的可解释性。部分新提出的题目相对难度评估模型(例如基于深度学习框架的知识追踪模型)虽然有效提高了题目难度预测的准确性,却存在模型在教育层面可解释性不强的问题。因此可以考虑将题目相对难度评估模型的设计和各种教育心理学理论(例如自我决定理论和Bloom 教学理论)相结合,从而让题目相对难度评估过程更符合教育过程的自然规律和学生心理发展规律,进一步提高现有模型的可解释性。
(6)缺乏基于教学反馈的题目难度评估方法改进策略的研究。题目难度评估往往仅是解决教学领域具体问题(例如个性化题目推荐问题和考试组卷问题)的前置条件。因而,如何充分利用题目难度评估方法所量化的题目难度信息来改进教学过程并基于教学过程的反馈信息来针对性地进一步改进现有题目难度评估方法也是值得实践和研究的问题。

