Numerical simulation of two droplets impacting upon a dynamic liquid film

Quan-Yuan Zeng(曾全元) Xiao-Hua Zhang(张小华) and Dao-Bin Ji(纪道斌)

1Three Gorges Mathematical Research Center,China Three Gorges University,Yichang 443002,China

2College of Science,China Three Gorges University,Yichang 443002,China

3Engineering Research Center of Eco-environment in Three Gorges Reservoir Region,Ministry of Education,China Three Gorges University,Yichang 443002,China

Keywords: two droplets,moving liquid film,CLSVOF,mechanism analysis

1. Introduction

As a common phenomenon in life, droplet impact plays an essential role in the development of agriculture and industry, for example, spraying crops and watering in the agricultural field. In addition, oil droplets impact the diesel engine combustion chamber’s inner wall, inkjet printing, spray painting[1]and often appear in the industrial field. Owing to the problem involving essential practical applications and complex motion processes, this has received extensive attention from many scholars at domestic and international level.At present,the methods for investigating this problem mainly include two aspects: experiment and numerical.

In the aspect of the experiment, Romainet al.[2]experimentally studied a drop impingement on solid surfaces. The experimental outcomes indicated that the phenomena of fusion, crown, splash, fracture, and rebound could be observed during the impact stage. Considering the problem involved plenty of physical parameters, and the systematic research was very complicated, plenty of scholars elected to research the influence of some critical parameters in detail. For example, Wang[3]studied dimensionless parameters: Weber (We),Reynolds(Re)and Ohnesorge number(Oh). They drew a conclusion that when the number ofWeandReis large,splashing occurs during the impact stage by experimenting. Okawaet al.[4]gave the criterion for splashing dimensionless numberK=We·Oh-0.4, while droplets hit a stationary liquid film.Guo[5]investigated the influence of the liquid’s viscosity and surface tension,moreover,liquid film thickness was taken into account. Experimental results showed that the viscosity and surface tension have an inhibitory effect on the generation of splashes. In addition,film thickness has a significant influence on the height of splash. Kang[6]investigated a droplet’s initial impact velocity and liquid film thickness on the impact behavior. Analysis showed that the diameter of the crown and the height of the central jet are mainly affected by the initial impact speed and film thickness. Moreover, the faster the initial impact velocity the thicker liquid film, resulting in a higher height of the central jet. Yao[7]researched the impingement of a droplet on an inclined surface with differentWeand impact angles by experimenting. Their analysis indicated that the size of the spreading diameter expands with the increase ofWe, and reduces with the increase of the inclined angle of the oblique surface. Some experiments about moving film were conducted as well, such as Castrej´o-Pitaet al.[8]observed splashing,bouncing and surfing phenomena by doing droplet impact experiments on a moving liquid film.Gao and Li[9]investigated the evolution characteristics of a single drop impacting dynamic film by experimenting. During the impacting stage, a significant asymmetric crown was observed. An experiment was conducted to study droplets impinging on dynamic liquid films at high Weber numbers,and the experimental results revealed scattered holes and basal crown separation.[10]

In the aspect of numerical,Rieber[11]considered a threedimensional(3D)model via a volume of fluid(VOF)approach to study the process of droplets hitting a liquid film. Through comparison, it is found that the simulation results are consistent with the experimental results. Raman[12]conducted the lattice Boltzmann method(LBM)to imitate the impingement of a double droplet on a liquid film. In addition,they analyzed the influence of different densities and viscosity of the twophase properties. Simulation results indicated when changing the density of air and the viscosity properties of the liquid,which has a great influence on the generation of the central jet. Liang[13,14]employed a coupled level set (LS) and VOF (CLSVOF) approach, and a two-dimensional (2D) numerical simulation of the splash phenomenon caused by the droplet hitting the liquid film is carried out. Outcomes indicated that the pressure difference is an essential cause of neck jet formation. He also conducted the simulation of a 3D physical model, which is a continuous impingement of three droplets on a liquid film. In addition, the pressure and velocity fields are analyzed to explain the formation mechanism of the central jet. Owing to crowns being frequently unstable, the tip of jets are prone to rupture and produce minor droplets. Various mechanisms had been put forward to cause tip rupture.[15,16]The Rayleigh-Taylor and Rayleigh-Plateau mechanisms are regarded as the reason for the liquid sheet instability.[17]Dai[18]via a CLSVOF method to numerically study and analyze droplets hit the oblique liquid film.Moreover, the influence of the oblique angle on the entrainment phenomenon stage was discussed. The result showed that when the impacting angle increases, the amount of bubbles entrained in the liquid film decreases. It is the pressure difference that causes front splashing, while the radial flow in the membrane causes back splashing. Guo and Lian[19]conducted a 3D model, studied a double droplet with different speeds and inclined angles to hit a liquid film. Numerical outcomes indicated that the high-speed impact of the droplets caused the crown to rupture and form splashes. Liu[20]used the LBM method to study a single droplet that impinges with a horizontal initial velocity on a stationary liquid film. Moreover, the effect of Bond numbers (Bo),We, and dimensionless liquid film thickness are investigated. Chen[21]employed a CLSVOF method to study droplets hit on liquid films with different thicknesses. In their work,the velocity and pressure are analyzed in detail. In addition, the influence of continuous drops impact on the liquid film is taken into account.The results showed that with the film thickness increasing,the crown diameter expands, in contrast to the height reduction. Moreover,with a successive drop impingement on film,secondary spurting is more likely to occur while the time gap between drops impact increases. Zhao[22]simulated and analyzed the single droplet impinging dynamic film on the 2D physical model. The CLSVOF method is adopted and the influence of the thickness is taken into account. In addition, a mathematical model of droplet spreading is derived and verified on dynamic film. Wang and Guo[23,24]implemented numerical study to explore the influence of droplet tilted hit static liquid film on flow characteristics and heat transfer. Outcomes indicated that asymmetric characteristics of surface heat flux were observed and the impact angle had no significant effect on the average surface heat flux. Besides,impact angle can inhibit or enhance crown formation. Simultaneously, the value ofWehas an important effect on the splash.Cheng and Lou[25]pointed out that dynamic films can enhance or inhibit splash.Heet al.[26]explored the collision of droplets with dynamic film by the LBM method,and outcomes showed that the movement of film led to asymmetry of crowns on both sides,which could inhibit the height of the crowns.

Nevertheless,a great number of experimental and numerical research work on droplets impingement has been studied to date. Most of them are about a dry surface or stationary liquid film,although there are some studies on impact of dynamic film, but the research work on the flow characteristics of the double droplet impacting the moving film is still insufficient.Thus,it is necessary to investigate the droplet impact on flowing liquid film. This work is based on the OpenFOAM platform,which employs a CLSVOF method to capture the splash characteristics of a double droplet impacting a moving liquid film. In addition, the mechanism of evolution phenomenon produced in the process of impacting the moving liquid film has been analyzed, and some conclusions have been drawn.The rest of this paper is organized as follows. In Section 2,the physical and numerical models are introduced. The numerical model is validated in Section 3. At last,the simulation results and conclusions are listed in Sections 4 and 5,respectively.

2. Computational domain and numerical method

2.1. Computational domain

In our work, the computational domain and parameters are shown in Fig.1,whereUfindicates the moving liquid film velocity andU0is the impact speed.Hfrepresents moving film thickness.Sis the horizontal central distance between two droplets, andgandDare the acceleration of gravity and droplets diameter,respectively. The related parameters can be seen in Table 1.

Table 1. Related parameters.

Fig.1. Physical model of a double droplet impact on a moving liquid film.

WhileUf=0 the film is a stationary liquid film, no-slip and pressure outlet conditions are employed in the bottom and top boundaries, and the sides are considered to be symmetry boundary conditions, respectively. For the case of moving liquid film(Uf/=0),no-slip and pressure outlet conditions are employed in the bottom and top boundaries, the sides are adopted periodic boundary,respectively.

This work adopts a 2D physical model. In our simulations, the computational domain employs 30 mm×10 mm.The acceleration of gravitygis taken into account. When two droplets impinge a dynamic film, there are four assumptions that need to be taken into account. (i) The liquid and droplet are the same incompressible Newtonian fluid, and the initial shape of the droplet is round. (ii)The impact process is laminar flow. (iii) The droplet and liquid phase changes are not considered. (iv) At the initial time, the droplet is tangent to the liquid film.

2.2. Numerical method

The present numerical study is performed using the Open-FOAM (Ver 2.4.0), an open-source software. In order to obtain the two-phase interface, in our work a CLSVOF method is employed, which makes full use of the advantage of the level set (LS) to capture the deformation of complex interface and topological structure changes,besides VOF maintains the conservation of mass well. Simultaneously, it overcomes the disadvantages of the non-conservation of quality of the LS method,which is not easy to calculate interface normal and interface curvature. In order to make full use of the advantages,coupling both methods to be implemented within interFoam solver in OpenFOAM is highly favorable.

2.2.1. Governing equations

The droplets impacting on moving liquid film are a typical two-phase flow problem. For a typical VOF model, the volume fraction functionαwould be solved in

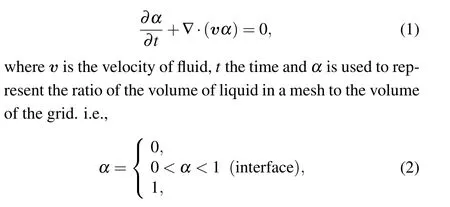
whenα=0, the cells are filled with gas, while the cells are filled with liquidα=1. When the cells contain both gas and liquid, the value ofα ∈(0,1), which means the interface between the gas and liquid.

Different from the general VOF equation,in OpenFOAM theαequation is calculated as

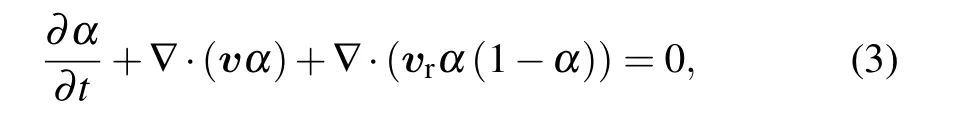
the extra third term is called the artificial compression term,which is compared with Eq. (1). The purpose of adding this term to the equation is to make the two-phase interface sharpen. Moreover, the two-phase relative velocityvris controlled by the coefficientCαand defined as follows:[27]

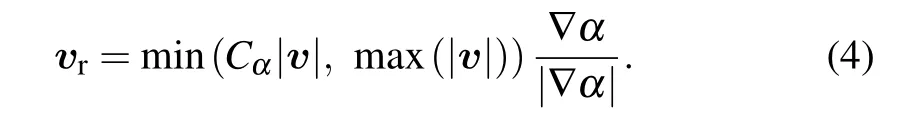
This coefficientCαis artificially given by the user,the purpose is to adjust the compression effect. If there is no compression, this givesCα=0, while the value ofCα=1 indicates conservative compression, and the last item isCα ＞1 which represents a high compression.[28]

To provide a more precise interface,a sign distance functionφis introduced. The functionφis defined as

theσindicates surface tension coefficient and the curvatureκcan be calculated as below:

andΥ=1.5Δxis the interface thickness.[29]

2.2.2. The process of the implemented CLSVOF method in OpenFOAM

The CLSVOF solver is based on interFoam in Open-FOAM (Ver 2.4.0). Solve the pressure equation and correct the velocity field alternately during each time step following the PISO-semi-implicit method for pressure-linked equations(PIMPLE)algorithm.[30]Moreover,the time step is automatically controlled by the maximum value of the Courant number,and some details are given as follows:

1. Define vector and scalar fields includingv,p,ρ,µ,α,H,Dirac function(δ),φ,etc.

2. Then,the VOF,LS functions are initialized. Moreover,calculate theδandH.

3. Next,start the time loop.

4. Solve theαequation and correct the new values ofα.Then,calculate the new LS function.5. Re-initialize theφby

3. Model validation

This section is divided into two parts. In the first part,we make a grid independence verification. For the 2D situation, the simulation of a drop collides with dynamic film is carried out using different grid densities. Figure 2 shows the schematic diagram of the height of the peripheral jet and Fig.3 shows the relationship between the grid and the height of the peripheral crown (HLandHR). Within 2 s, the height of the left crown wall and the right crown increased with the amount of the grids;and after 2 s,due to the right crown wall splashes,the result is a difference in the height of the right crown.When the amount of grids reaches 8×104, the height of crown has no bearing on the amount of the grid cell. Therefore,each of cases in our simulation employs the 8×104mesh number.

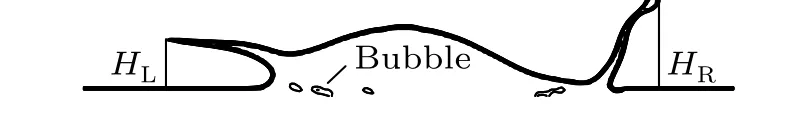
Fig.2. Schematic diagram of the height of peripheral jets.

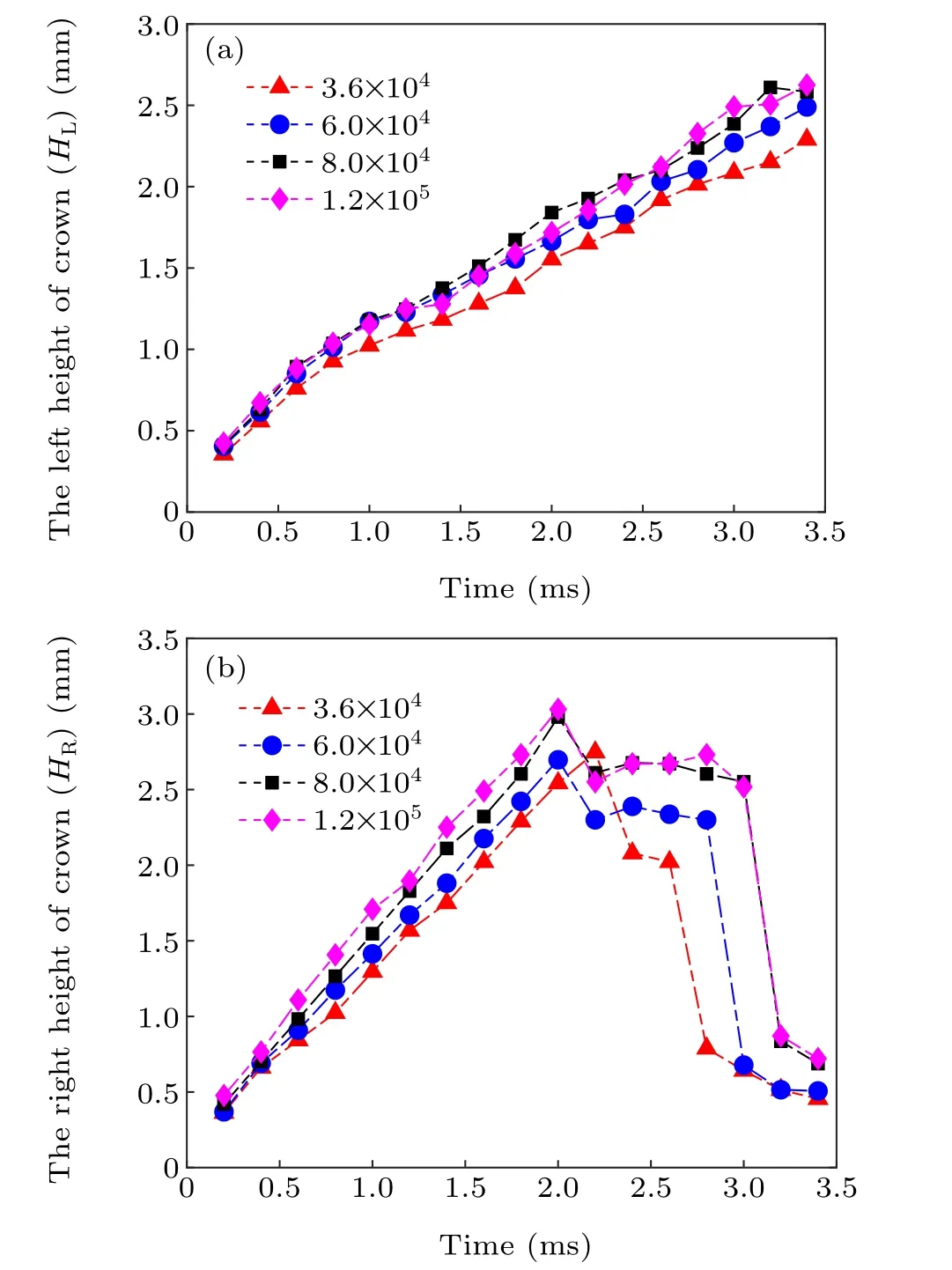
Fig.3. The relationship between peripheral jets and time under different grid densities.

For the second part,to validate the correctness of our numerical model. As is shown in Fig.4,which a comparison between our simulation evolution interface with the experimental results of Gao and Li in reference,[9]where the diameter is 3.2 mm, the impact velocity is 1.85 m/s, the film velocity is 1.04 m/s, and the film thickness is 0.209 mm. The same parameters are applied in our simulation as well. There is something to be noticed that from the results of Fig. 4, the CLSVOF method can better capture the splash characteristics when a drop hits a dynamic film. Meanwhile, bubble retention phenomenon is observed. In addition,our simulation is in good agreement with the reference.[31]Additionally,as shown in Fig. 5, we quantitatively compared the experimental result of reference[32]with our simulation outcome. The parameters givesU0=3.51 m/s,D0=3.82 mm,Hf=2.57 mm andWe=667. We find that the results of our numerical simulations and the experimental measurements are in general agreement. Thereby verifying the reliability and correctness of our model.

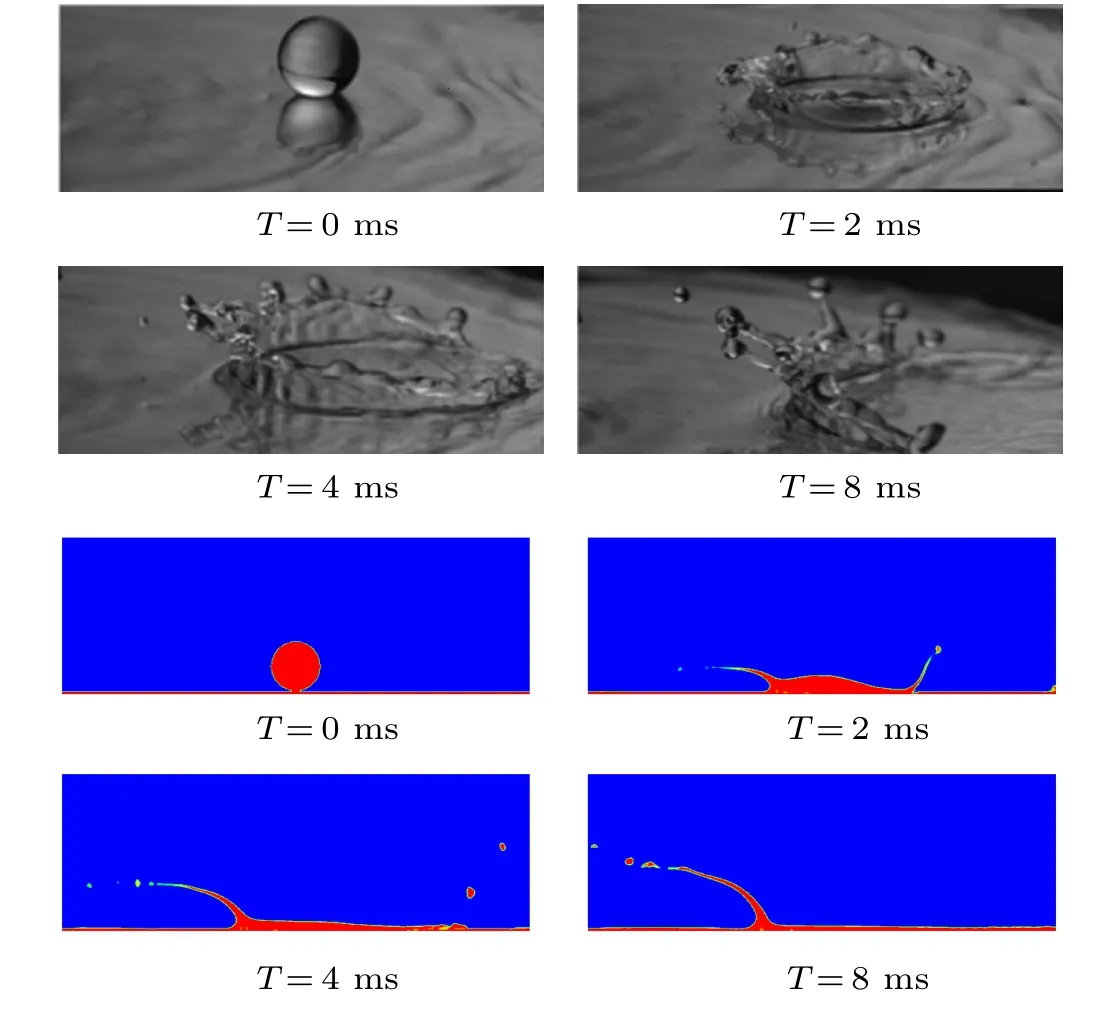
Fig.4. The results of experiment and simulation.

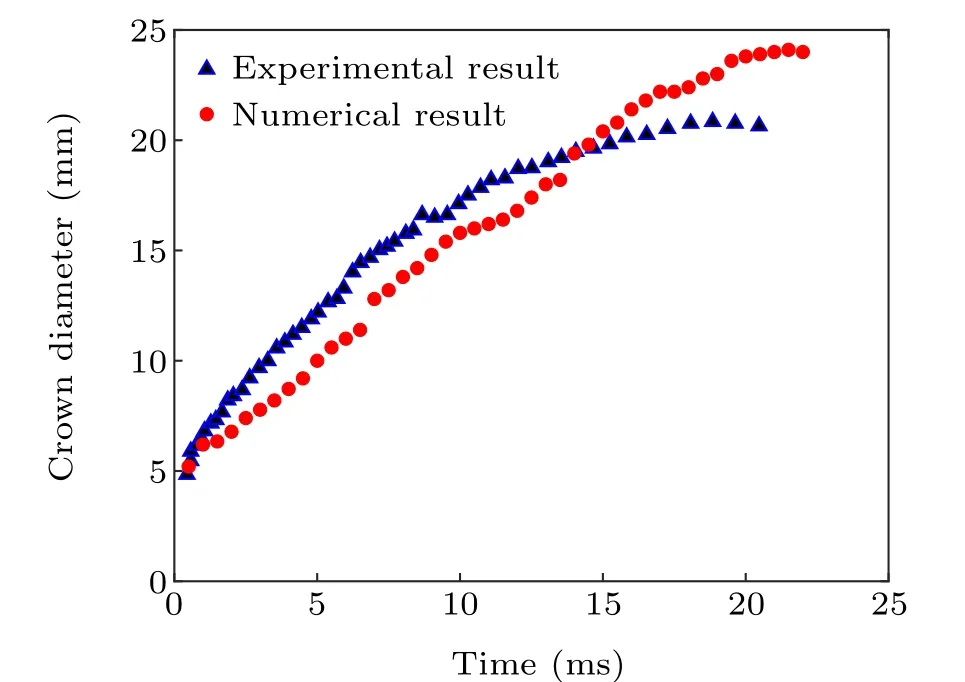
Fig.5. The results of experiment and simulation.

4. Simulation results and discussion

In this section,the influence of two-droplet impingement on a dynamic film is taken into account. Simultaneously, the dynamic film thickness,initial impact velocity,the horizontal central distance between droplets, and film speed are considered. In order to depict the interface evolution phenomenon and analyze the mechanism of droplets impacting, some critical dimensionless parameters including the droplets central distanceS∗,film thicknessH∗,the velocity of liquid filmU∗,We,Re,andOhare listed below:

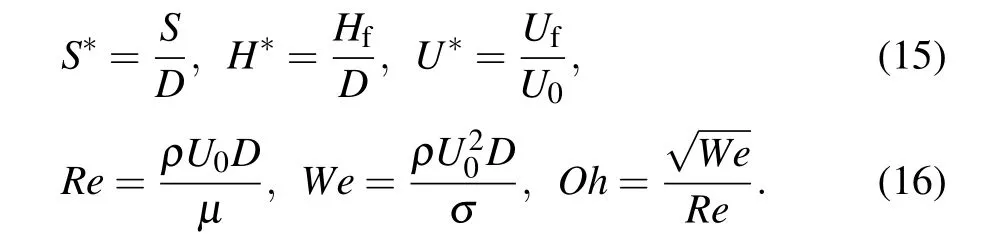
4.1. Asymmetric crown and splash behavior

Figure 6 shows the morphological evolution of two drops that impinge on static and dynamic film, respectively: the thickness of filmHf= 2.09 mm, the impact velocityU0=1.85 m/s, the central distance of dropletsS=6 mm. For the stationary liquid filmUf=0 m/s,while the moving liquid filmUf=1.04 m/s. It is obvious that while droplets impact the stationary liquid film,symmetric characteristics can be found.Simultaneously, asymmetric phenomena can be observed in right case. At the beginning of the impacting stage, both of them have similar evolutionary phenomena. Four fine jets are formed on the left and right sides of the two droplets. After 0.8 ms, for the left case, the symmetrical characteristics of evolution still exist,while for the following liquid film,the symmetry characteristic disappears. In addition,it can be observed that the peripheral jets are growing in an oblique direction for the stationary film, and the jets between the two droplets merge to form a single central jet. Different from the stationary liquid film, the peripheral jet of the upstream droplet becomes a horizontal jet. The development direction of the central jet is the opposite of the dynamic film flow rate.Simultaneously,for the right case splashing characteristics can be observed,while for the left case,no splash occurred.

Figure 7 shows the vector field distribution of the two droplets whenT=0.4 ms. Yarin and Weiss[33]pointed out that the main factor in the formation of the crown wall during the impact is caused by the discontinuity in kinematics.We note that a kinematic discontinuity can be seen at the impact contact points (A,C) in the speed vector diagram.Whereas, at the impact contact points (B,D), kinematic discontinuity is not apparent, which draws the same conclusion in reference.[22]The reason for this phenomenon can be explained by the downward velocity generated when the droplet hits the dynamic liquid film,and when it contacts the wall,the velocity direction changes from downward to radial; the incoming flow from upstream obstructs the fluid moving radially upstream,so that the velocity field has a motion discontinuity near the upstream contact points(A,C); however, the motion discontinuity near the downstream contact points(B,D)is not obvious because the direction of the liquid film velocity is consistent with the radial motion to the downstream.

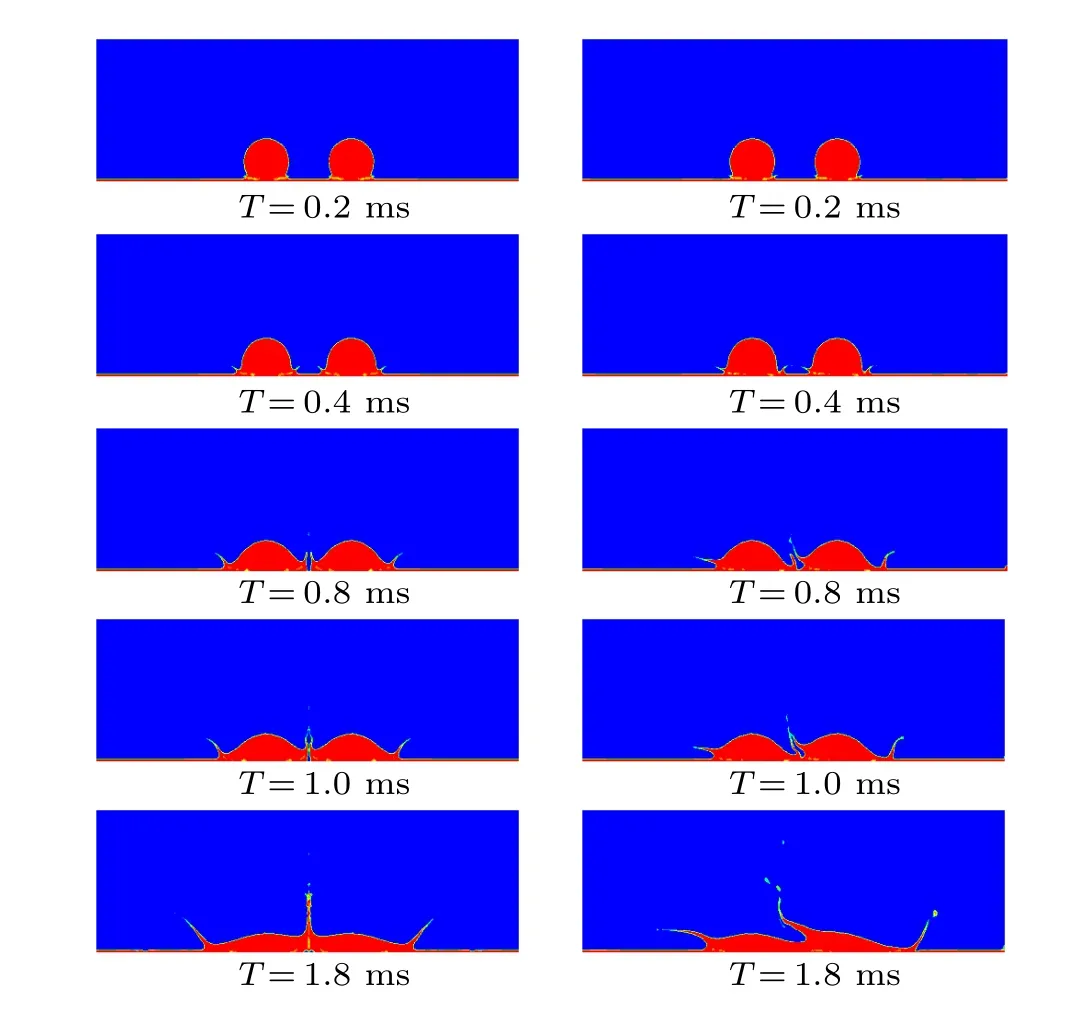
Fig.6. A double droplet impact on film,left on a stationary liquid film,right on a moving liquid film.

Fig. 7. (a) Vector distribution at T =0.4 ms, (b) and (c) local enlargement near points A and D.

Figure 8 shows the pressure field distribution of the double droplet hit the moving liquid film. Obviously, at the beginning stage of impingement,the pressure decreases from the bottom to the top.With the impact continuing,the two droplets move radially outward,and the pressure gradient on both sides gradually decreases. Moreover,the pressure in the region between the two droplets becomes larger, and the range of the high-pressure zone continues to shrink,the maximum pressure decreases. From the pressure distribution, it can be observed that the internal pressure magnitude of fluid is imbalanced. In addition,the value of pressure magnitude near the impact contact points(A,C)is much higher than pointsBandD. WhenT=0.8 ms the pressure near the pointCis relatively higher than other region, the points are shown in Fig.7. The reason is that the radial movement near the contact point on the right side of the two droplets is consistent with the flow direction of the moving liquid film. In addition,the pressure difference between the jet necks is usually higher than the pressure difference at the two-phase interface,which causes the peripheral jets to form in the neck,and the central jet is formed between the droplets. The asymmetric characteristic of the evolution phenomenon is essentially the liquid film is non-stationary.

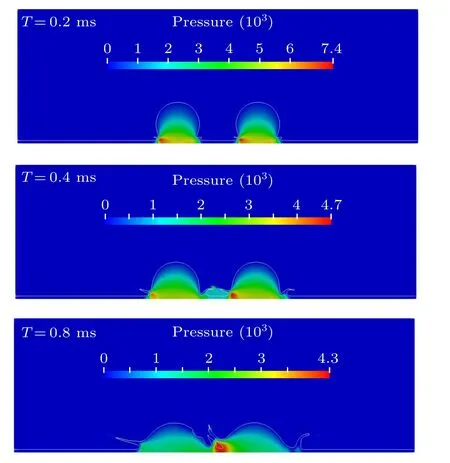
Fig.8. Pressure distribution after droplets simultaneously impact the moving liquid film.

During the impact,on the one hand,as the droplets continue to collide, the surrounding liquid continues to enter the crowns area, on the other hand, by the mutual transformation of droplets’ energy, leading to the jets becoming higher gradually. Owing to the instability of Rayleigh-Plateau,[34]at the top of the jets prone to splashing phenomenon,leading to minor droplets,the simulation results in Fig.6 captured the splashing phenomenon as well.Gao and Li[9]indicated that as droplets strike a dynamic film,the critical value for splashingK1is given as 3378,i.e.,

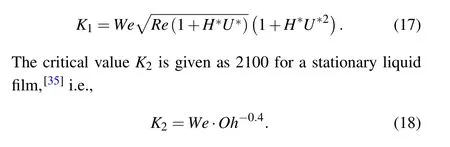
In the present simulation,K1andK2are 12079 and 1787,respectively. Thus for the moving liquid film, the splashing phenomenon can be captured. Splashing characteristics cannot be observed for the stationary liquid film, which is basically consistent with our simulation results.

The splashing of droplets and the breaking of the crown produced during the impact are actually caused by the instability of the crown. Rayleigh-Plateau instability refers to the development of instability that is exacerbated by the flow of fluid from the neck region to the expansion zone under pressure,leading to eventual fragmentation into tiny droplets.[22]

4.2. Influence of horizontal distance between droplets

Figure 9 shows the interface evolution of a double droplet impingement on a dynamic film with three different distancesS∗. The left case givesS∗=1.5625 and middle case givesS∗= 2.0 while the right case givesS∗= 2.5, moreover theWe=151,U∗=0.56 are adopted. We note that for a particular case,when theS∗is large enough,there is almost no effect between the upstream droplet and the downstream droplet. In addition,the main difference is that as the droplet spacing decreases,the smaller the droplet spacing is,the earlier and more intense the collision of the two droplets, the more instability at the two-phase interface, leading to droplets splashing earlier. At the same time, the radial speed of the dynamic film is still large, and the collision of the droplet and the dynamic film generates shear force, which makes it easier to develop the central jet. In the expansion process, the liquid splash is affected by the flow resistance, and the horizontal velocity gradually decreases;when the adjacent neck jets meet,the intermittent motion phenomenon occurs in the contact area,and the velocity deflects from the horizontal direction to the vertical direction. With the droplet spacing increasing, and the upward motion speed of the formed intermediate film jet decreases; therefore, the central jet height decreases with the increase of the droplets’distance.

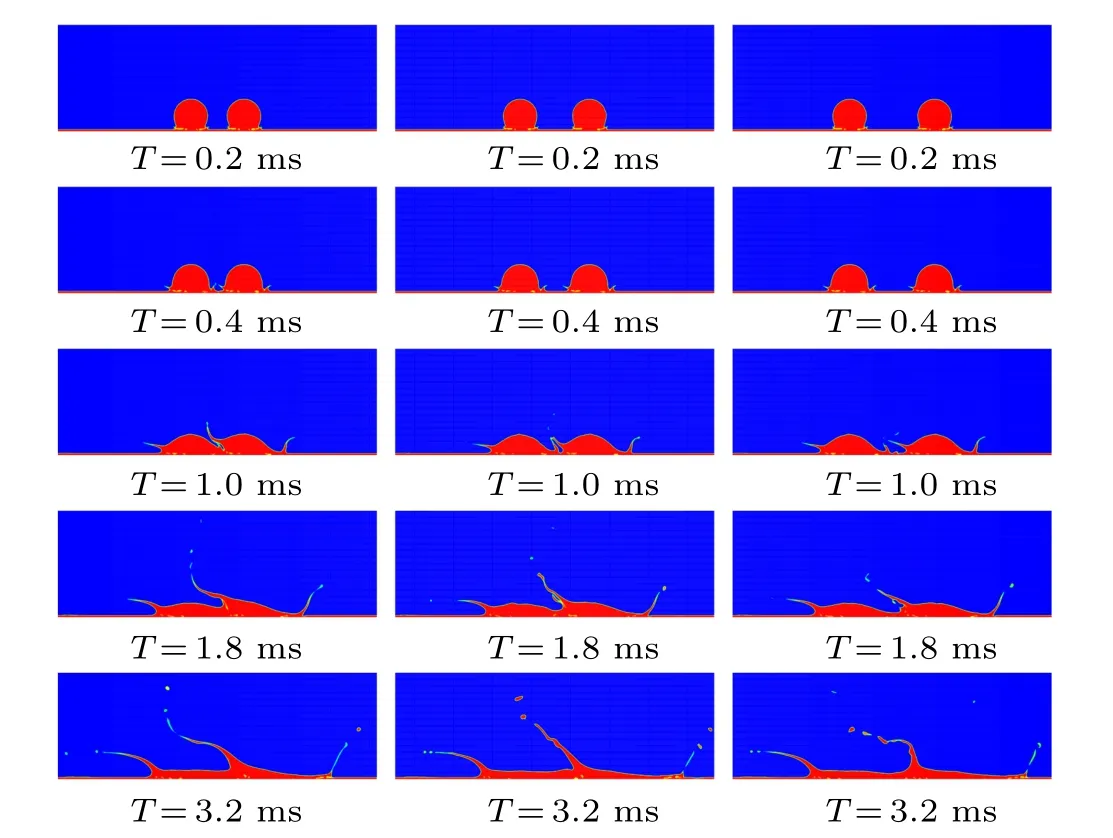
Fig.9. Interface evolution with three different droplets’central distance,left(S∗=1.56),middle(S∗=2.0)and right(S∗=2.5).

Figures 10(a) and 10(b) show the height of the left and right peripheral crowns with time under differentS∗, respectively. In the first 2.5 ms,the horizontal spacing of the double droplet has almost no effect on the height of the spray on both sides, the falling height of the splash is different, but the difference is not significant. The reason is that at the beginning of the impingement,the splash caused by two drops is similar to that caused by a single drop. When two droplets collide,the interaction at the middle position produces the central uprising jet, but within a period, the influence on the spray height of both sides is not apparent. Figure 10(c)shows the spreading length with differentS∗, we find that asS∗increases the spreading length increases as well. This can be attributed to that when the distance between droplets increases,the droplet interaction time becomes longer, resulting in a longer radial flow time at the bottom of the droplet and thus an increase in spreading length.

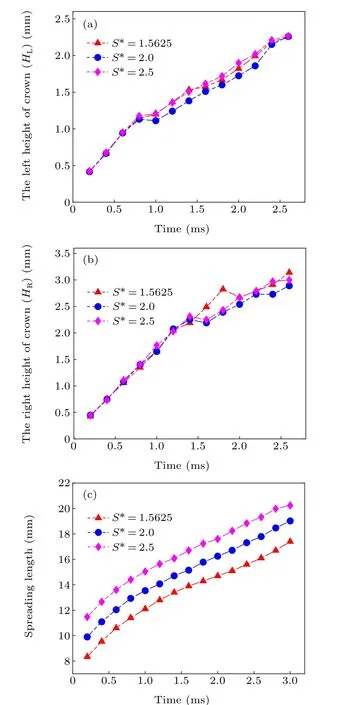
Fig.10.Peripheral jet height and spreading length with three different droplet spacing.

4.3. Influence of dynamic film velocity

Next,we analyze the influence of dynamic film speed on evolution characteristics. Figure 11 shows the evolution with three different velocities of the dynamic film where the left caseU∗=0.38 and middle caseU∗=0.56 while the right caseU∗=0.71,moreover the We=151,U0=3.2 m/s.

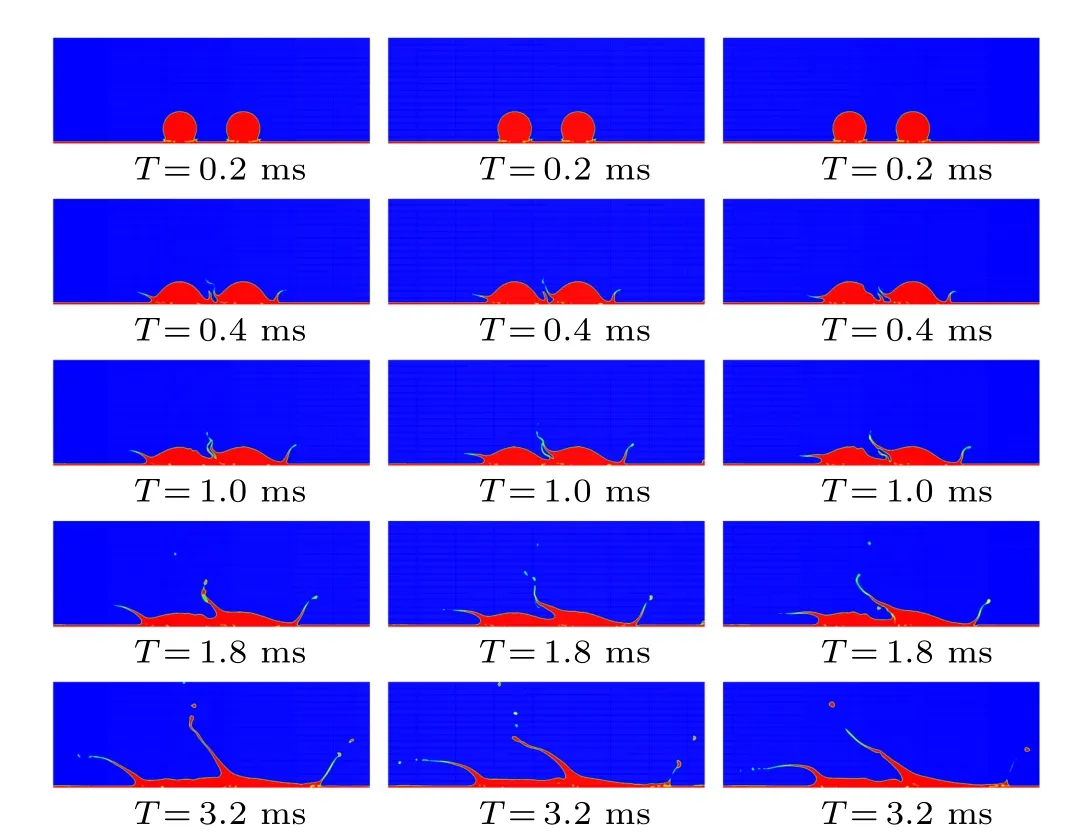
Fig.11. Interface evolution with different dynamic film velocity,left(U∗=0.38),middle(U∗=0.56)and right(U∗=0.71).

Due to different film velocities, various evolution phenomena occurred during the impact. At the beginning stage of impact,the evolution phenomenon of the three cases is resembled. There are four fine sprays appearing close to the collision area of the droplet and the moving liquid film. Furthermore, whenT=1.2 ms, the two droplets extend to both sides and form a crown; at the same time the two middle jets merge into a single. The difference is that,whenT=1.8 ms,for the moving liquid film with a larger velocity(U∗=0.71),the easier downstream jet splashes,the smaller the inclination angle between the left spray and central spray. In other words,the larger speed of the dynamic film, the more obvious the characteristics of the horizontal movement of the upstream peripheral jet. For a particular case,while theUf=0,the central jet is perpendicular to the liquid film,which is in good agreement with the left case of Fig.6.

Figures 12(a)and 12(b)show the heights of the upstream and downstream crowns at three different film velocities, respectively. The results in the figures show that the height of the upstream crown decreases significantly when the film velocity increases. While the height of the downstream crown does not decrease significantly at first, and afterT=1.8 ms,for a higher film velocity, the height of the crown displays a significant decrease. This is due to the fact that the radial velocity at the upstream impact pointAis opposite to the incoming flow velocity,thus remaining stable for a certain period of time,and the height of the crown is gradually increasing. On the other hand, it can be explained by the angle between the crown and the liquid film. As the flow velocity of dynamic film increases,the angle between the upstream crown and film decreases,resulting in an increase in the horizontal velocity of the crown and a decrease in the vertical velocity,thus decreasing the height of the crown. In the early stage of impact, the downstream jet height is caused by the radial motion of the film. Subsequently, the radial velocity decreases and the liquid film flow velocity plays a dominant role. When the crown reaches its maximum height, the splash of droplets is caused by Rayleigh-Taylor instability,and the surface tension plays a leading role in the later period,leading to the height of downstream crown decrease.

Fig.12. The spreading length and crown height with different film velocity.

Figure 12(c) shows the relationship between spreading length with time, we find that the length increases with the dynamic film velocity. In fact, at that time, the radial velocity no longer plays a dominant role in the spreading length;it is the moving liquid film with a larger velocity,leading to the fluid moving quickly to the right and the extended length of the downstream droplet increases. Leftward shear stress is produced between droplets and dynamic film,resulting in a case

where the jet has a tendency to tilt leftward, comparing with the dynamic film moving at a low velocity. WhenT=3.0 ms,for the higher velocity of dynamic film, the peripheral jet of downstream droplet disappears gradually. Simultaneously,the peripheral jet of the upstream droplet begins to descend. What is more, compared with the result in Fig.9, the dynamic film speed has a greater influence on the angle between the peripheral jet and film.

4.4. Influence of droplets impact velocity

Then,the two droplets initial velocity influence on interface evolution is investigated using three different values ofU0(U0=1.35 m/s, 2.0 m/s, and 2.85 m/s). Figure 13 shows the interface evolution phenomenon of two droplets hitting a dynamic film whereD=2 mm,S∗=2; the thickness of filmHf=1.2 mm.

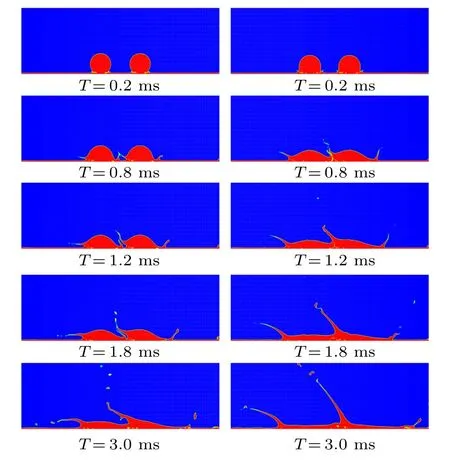
Fig.13. The evolution with different impact velocity of droplets,left(U0 =1.35 m/s),right(U0=2.85 m/s).

It is evident that the higher velocity merges the central uprising jet faster than the lower velocity. WhenT=1.2 ms,for the left case, the peripheral jet generated by the upstream droplet produces a horizontal jet,whereas the upstream droplet on the right case produces an inclined jet.

Figures 14(a) and 14(b) show the crown heights at different impact velocities. We find that the upstream crown height increases withU0. The downstream crown

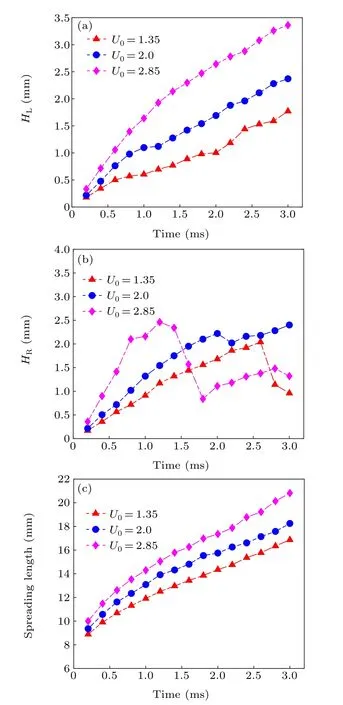
Fig.14. The spreading length and crown with different droplet initial impact velocity.

height also increases at the beginning of the impact,and when the impact velocity increases further, the crown height decreases instead.This phenomenon can be explained by the fact that during the initial impingement, the liquid continuously enters the jet under the effect of kinematic discontinuity,[36]forming a crown spray that leads to an increase in height and diameter. When the initial impact velocity increases, the initial kinetic energy of the droplet increases and most of the energy is converted into kinetic and potential energy of the crown spray, resulting in the crown being unstable, and the splash phenomenon occurs earlier at the same time. It is also influenced by the Rayleigh-Plateau instability,which leads to the formation of secondary droplets,and some of the liquid is thrown out,leading to a decrease in the crown height.

Figure 14(c) shows the relationship between spreading length and different impact velocities, outcomes indicate that the larger initial impact velocity the longer spreading length.The reason is that when the momentum of the droplet is large,a greater radial velocity is generated downstream of the droplet, the fluid in the impact area will extend faster to both sides,thereby increasing the spreading length. In addition,the right case with a higher impact velocityU0= 2.85 m/s the peripheral jets and central uprising jet have larger heights. Besides,the two peripheral jets move upstream and downstream respectively, compared with the situation that droplets with a lower speedU0=1.35 m/s. The reason is that, with a higher impact velocity,the droplets hit moving film drastically,causing the impact area to get slighter. Simultaneously,more fluid moves into the crown, resulting in an increase of the height and diameter of crown wall and central jets.

It can be seen from the velocity distribution as is shown in Fig.15 whenT=2.6 ms that since the moving liquid film flows in the horizontal direction, the liquid in the spreading edge area still remains at a certain horizontal velocity when it gets into the jet.Therefore,the jet has certain horizontal movement characteristics,which can explain that the peripheral jet generated by the upstream droplet is a horizontal jet in some cases. In addition, the outward expansion speed of the jet is much weaker than the radial movement speed of the liquid in the impact area. Therefore,a speed discontinuity is generated in the jet region, which promotes the formation and development of the jet, thus verifying the correctness of the motion discontinuity theory. Moreover, below the left peripheral jet,the vortex size and the angle between the left peripheral jet and the liquid film enlarges as the droplets’initial velocity increases.

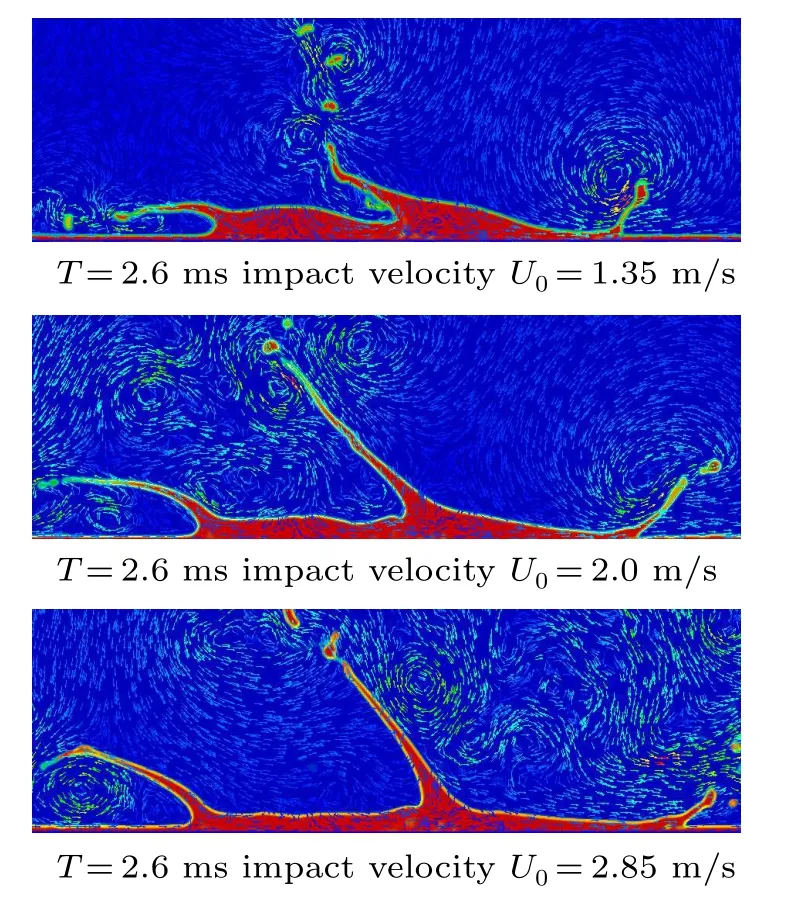
Fig. 15. Vector velocity and interface evolution with three different impact velocities when T =2.6 ms.

4.5. Influence of dynamic film thickness

We now discuss the influence of dynamic film thickness on the behavior of peripheral jets. Figure 16 shows the interface evolution with different thicknesses. TheWegives 151,U∗=0.4,H∗=0.1,0.2,0.4 respectively. TheK1value of the different thicknesses are 12323, 13034, and 14490 calculated via Eq.(17),the minimum ofK1is much higher than the critical value 3378,which indicated that we can capture the splash characteristic.

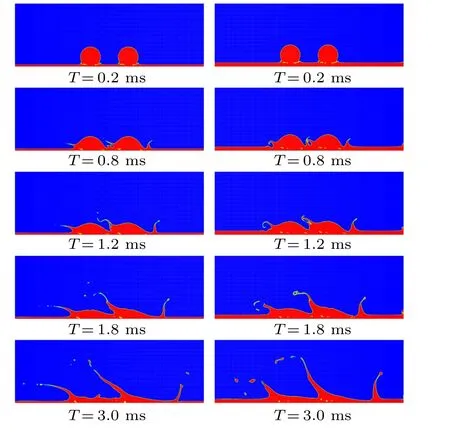
Fig. 16. The evolution with different thickness, left (H∗= 0.1), right(H∗=0.4).

Figure 17 shows the velocity and the vorticity distribution of the droplets hit different thickness of dynamic films whenT=0.4 ms. As is shown in the figures, for the right cases,a large vorticity near the top of the peripheral jet and the central jet exists, which means that splashing is more likely to occur at the top of the jet. For the left cases, it can be vaguely seen that there are clockwise and counterclockwise vortexes on the upper and lower sides of the upstream peripheral crown, respectively; whereas a single counterclockwise vortex exists in the downstream. However,the clockwise vortex upper the upstream crown is weaker than another opposite direction vortex,which leads to the left upstream crown having a counterclockwise development trend. For the same reason,the downstream peripheral jet bends in the clockwise direction. This conclusion is in good agreement with reference.[20]Namely,the peripheral jet on the left moves horizontally,and the right peripheral jet has a vertical development trend. Besides, as the dynamic film thickness increases, the vortex becomes smaller. This can explain the phenomenon that when the thicknessH∗=0.4,the angle between the downstream peripheral jet and the dynamic film is close to 90°at 3.0 ms. In reference,[38]the same evolution characteristics are observed with droplet impingement on a static liquid film. Therefore,the direction of peripheral jet development is closely related to the radial motion and vortex.

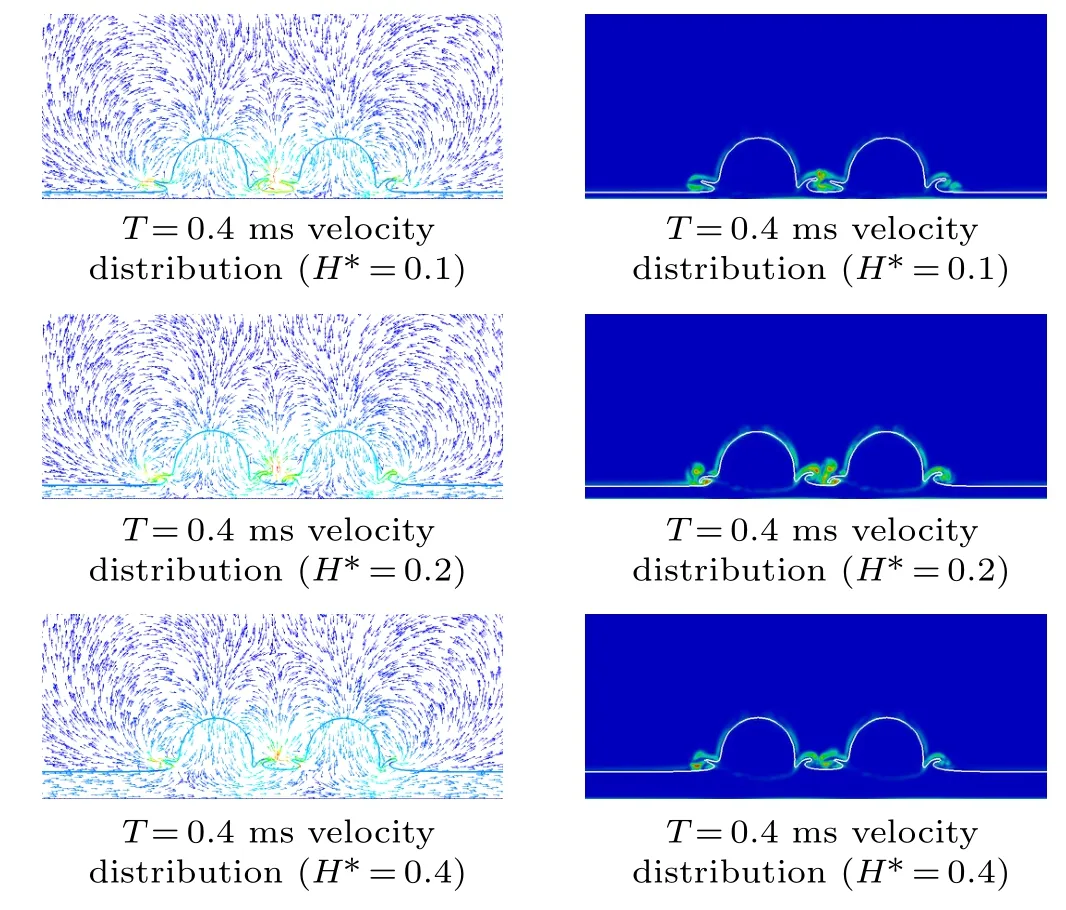
Fig. 17. Velocity and the vorticity cloud diagram when the droplets impact on different moving liquid films.

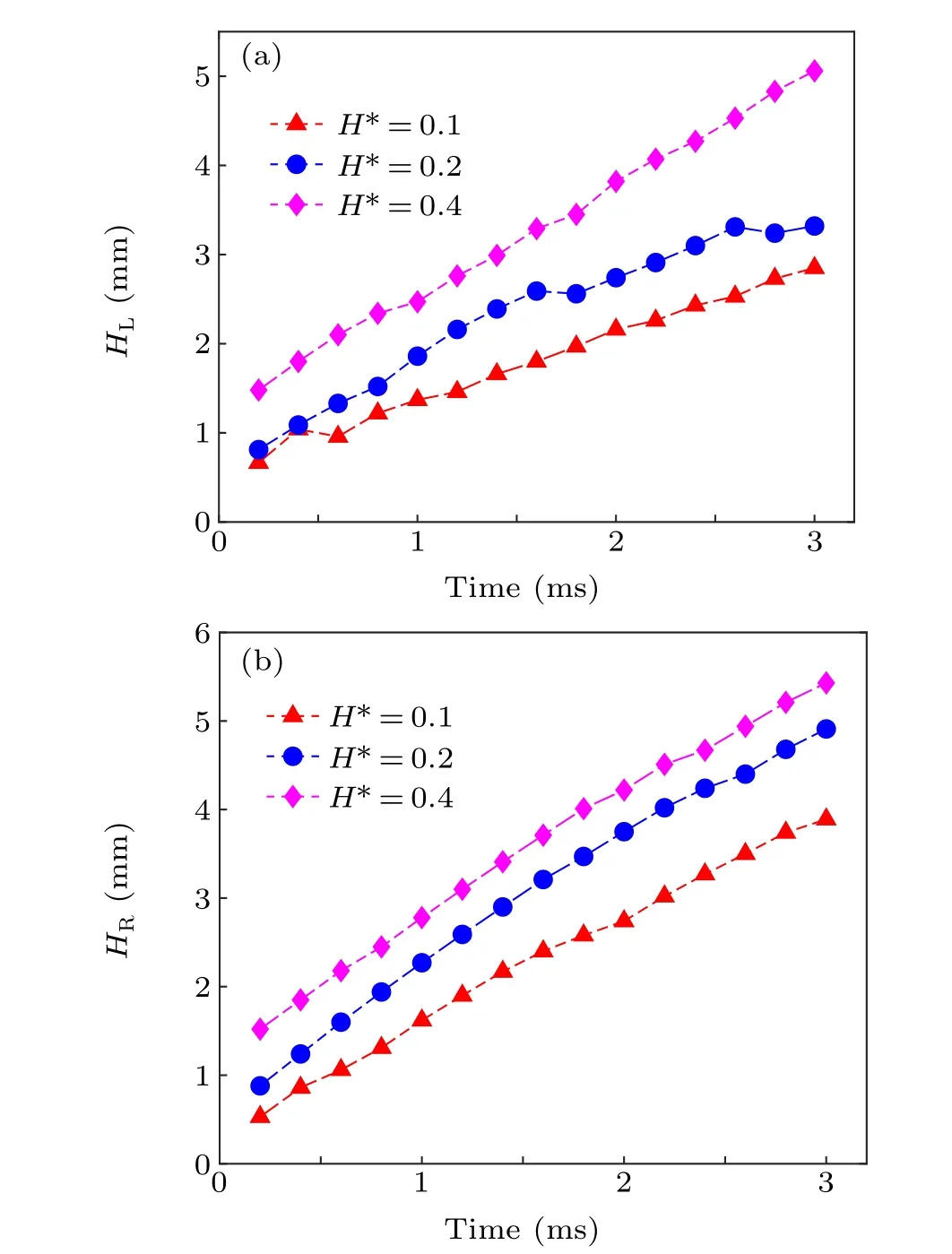
Fig. 18. The spreading length and crown height with different film thicknesses.

When the droplets start impacting on a thick dynamic film,droplets continue to squeeze the surrounding liquid. The resistance of the droplet diffusion and the loss of kinetic energy will increase.[37]For example,afterT=0.8 ms,the outer jet of the right case is stronger compared with the peripheral jet generated by the case on the left. The analysis shows that when droplets hit dynamic films of different thicknesses, the thicker the dynamic film,the larger the volume of fluid entering the jet, leading to an increase in the height of the crown,as in shown in Fig. 18, since the droplets have equal kinetic energy. At the same time, droplets of a larger size were produced, and this reason can be explained by the fact that due to the increase in the height of the crown, the droplets produced at the end of the crown were larger and the instability increased, when the surface tension was not enough to withstand the gravity of the droplets,leading to the shedding of the droplets, but at this time the height of the crown also did not show a significant decrease.

5. Summary and conclusions

In this work, a CLSVOF method is adopted to investigate the simultaneous impact of a double droplet on a moving liquid film based on OpenFOAM.The formation and development of the peripheral jet, central uprising jet, and the evolution mechanism were analyzed. In addition, the effect of dynamic film thickness,film velocity,initial impact velocity,and the horizontal distance between the center of the droplets was taken into account.The brief conclusions are listed as follows:

(I)Compared with the impact of droplets on a static liquid film,they have similar evolution phenomena in the initial stage of impingement; but an obvious asymmetry can be observed when impacting on a dynamic liquid film.

(II)Within a certain period,the droplet spacing does not affect the peripheral jet height; as the droplet spacing decreases,the droplets splashing earlier.

(III)By increasing the film velocity,the crown height can be suppressed,so that the crown becomes more stable;and the horizontal movement characteristics of the left peripheral jet is more obvious.

(IV)By increasing the impingement velocity,the result is a rapid increase in crown height in the early stages, and the crown is very unstable, which subsequently leads to a rapid decrease in crown height as a result of the fluid being thrown out of the crown. In addition,the greater the impact velocity,the greater the angle between the upstream peripheral jet and dynamic film.

(V)When the film thickness is increased,it leads to larger secondary droplets and rims,and the surface tension is not sufficient to overcome their gravity, leading to the shedding of secondary droplets.

(VI) The spreading length increases with the velocity of dynamic film,droplet spacing and initial impact velocity.

Acknowledgment

Project supported by the Engineering Research Center of Eco-environment in the Three Gorges Reservoir Region(Grant No.KF2019-10).