多孔介质细观流动理论研究进展

朱维耀，李 华，邓庆军，马启鹏，刘雅静

1) 北京科技大学土木与资源工程学院，北京 100083 2) 大庆油田第一采油厂，大庆163000

多孔介质广泛存在于地下岩石、生物仿生和工程材料中，但由于多孔介质内孔隙微小、复杂且其中流体(液体和气体等)的流动理论尚不完善，使得大量多孔介质内流体的流动问题亟需解决，如页岩油气开发、土壤渗流、人体毛细管网络和碳纳米管(Carbon nanotube，CNT)等. 目前研究人员大都将多孔介质内流体的流动尺度划分为细观尺度(特征长度l=10 nm～1 mm)和宏观尺度(l＞1 mm)两种[1-2]. 随着微电子机械系统（Micro electro mechanical system，MEMS）、3D模型打印技术、原子力显微镜 (Atomic force microscope，AFM) 、表面力仪 (Surface force apparatus，SFA)、显微离子测速仪 (Micro/Nano particle image velocimetry，Micro/Nano PIV)、岩心重构和孔隙网络仿真模拟等技术的诞生和不断进步，多孔介质中流体的流动理论在近些年来已经得到了相当的发展，尤其是对细观尺度下的多孔介质内流动理论及其相互之间耦合作用的研究现已成为石油工程、地质学、地下水水文学和生物渗流等领域研究者所关注的重要课题[3-5].

石油工程领域对多孔介质内流体流动理论的研究主要是针对宏观尺度下的流动，其基本假设条件是连续介质场[6]. 但随着“美国页岩气革命”的成功，石油开发过程中多孔介质中流动特征尺寸不断减小，由宏观（Macro scale）逐步转向细观（Meso scale），特别是纳微米孔隙（如超低渗、页岩/致密油气储层多孔介质等）[7-8]. 因此，随着大家对细观尺度的多孔介质越来越感兴趣，关于细观流体力学的发展将面临很多全新的挑战，比如如何修正宏观动力学方程和边界条件以适应细观流动问题的研究，在细观尺度下如何解释多孔介质内流体流动机制，以及如何构建考虑微观力作用的孔隙网络模型等，这些问题都需要进一步去探索[6,9-10].本文致力于关注多孔介质细观流动理论的发展现状与应用前景，提出了当前多孔介质细观流动理论发展所面临的基本科学问题，综合分析了针对目前石油工程领域所面临的实际问题以及与之对应的多孔介质中细观流动理论的研究进展，同时介绍了本课题组研究的一些最新成果，以期为未来多孔介质内细观流体的流动机制的完善和工程实际应用提供一定的理论指导.

1 多孔介质细观流动研究的历史回顾

多孔介质中细观尺度流动所基于的影响因素与宏观流动不同，主要差别表现在非线性渗流、连续介质假设条件、微尺度效应和表界面微观力，由于不同研究者在研究条件和实验方法等选取上的不同，其结果也各有差异[11-12]. 关于细观尺度的流动问题早在20世纪70年代的“芯片式制冷器”[13]和“色谱仪”[14]的工作中就引起了部分研究者们的关注，他们起先研究的是关于气体在微管道内的流动[15]；80 年代后，一些学者对微尺度下的液体流动问题也有所关注，但由于液-液/液-固间微观力作用的存在，使其力学特性更加复杂[16]；90 年代“微流控芯片”技术的被应用于微流动的实验和模拟，以研究微观尺度下界面作用对流体运动规律的影响[17-18]；随着21世纪后“纳米技术”的飞速发展，针对多孔介质中微流动的研究更加火热，如各种微观力对多孔介质中微流动的影响[19]、利用分子动力学（Molecular dynamics，MD）手段研究微流动过程中的界面现象[20]、格子玻尔兹曼（Lattice Boltzmann method，LBM）[5]和多孔介质网络模型的重构模拟多孔介质中的流动问题等[9,21-23].

1.1 理论分析

流体流动的理论描述，需要明确正确可解的连续方程、动量方程和边界条件[24]. 1856年达西定律（Darcy law）的提出为多孔介质中流体流动问题的理论研究奠定了基础，如在石油工程中达西定律是油气在岩石孔隙中流动的基本场方程[25-27].2002 年 Civan[28]利用努森数（Knudsen number，Kn）的范围，将气体流动分为连续流、滑移流、过渡流和自由分子流，横跨多个特征尺寸且有相应的流动基本方程，如图1所示[29]. 本部分主要介绍在修正细观尺度流动中的基本场方程和边界条件时所考虑的关键因素，如多尺度效应、流体微可压缩性、界面效应和微观力等.

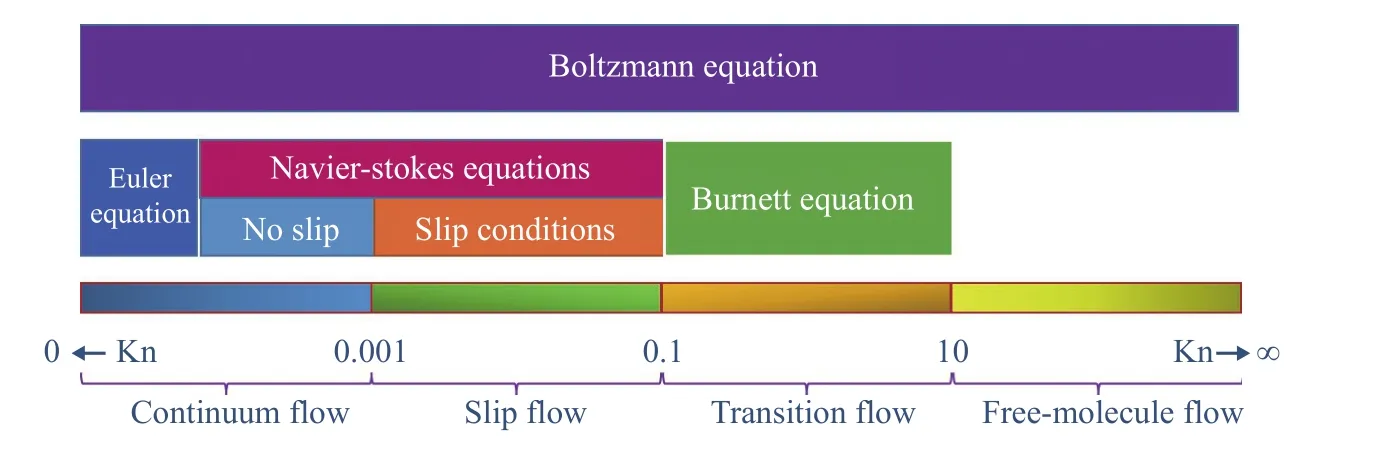
图1 不同“努森数”下的气体流动方程[29]Fig.1 Gas flow equations at different “Knudsen numbers”[29]

多孔介质细观流动中的“尺度效应”十分明显，由宏观尺度（l＞1 mm）到细观尺度（l=1 nm～1 mm）特征尺寸缩小了近6个数量级，甚至更小，因此在研究细观流动问题时首先要考虑流体本征尺寸和多孔介质适配性的问题，以及由尺度范围变化所引起的多尺度效应[30-31]. Keenan与Neumann[32]通过研究管道（直径d=1～2 mm）内可压缩气体的流动问题后发现在湍流情况下与在大管道中的流动无异. 但随着人们研究的微通道尺度（直径d=1 nm～1000 μm）的不同，摩擦系数（Frictional coefficient，λ）与雷诺数（Reynolds number，Re）的乘积也略微偏离常规值，如著名的哈根-泊肃叶定律（Hagen-Poiseuille law，H-P）[33]. 目前滑移边界条件已经得到大多学者的认可，并先后提出了表面润湿性、表面气体层和表面粗糙度等理论，但是对于实际中流体是形成黏滞层还是如线性滑移模型所述直接在固体表面产生滑移依然存在一定争议[11,24]. 界面作用是导致微流动不同于宏观流动的主要原因，对于细观流动界面间的相互作用力的大小受到管道的截面形状、变形率和粗糙度的影响，也和流体性质比如流体的极性、压缩性以及流体内是否含有气泡等因素密切相关[9,19,34]. 关于液体微流动目前仍没有完善的分子动力学理论，也没有类似Kn数的量纲一的参数将宏观与细观相联系，目前针对细观尺度流动理论研究集中于液体，如固液界面滑移、电黏动力学效应和微观力效应等[11].

1.2 实验研究

纳微米实验测量仪器研究多孔介质中细观尺度下的流体流动问题是研究人员所采用的最直接的手段，如原子力显微镜/表面力仪（AFM/SFA）[35]、氧化铝薄膜（Porous anodia alumina，PAA）[36]、微圆管（Microtube，MT）[10]、Micro/Nano PIV[37]、微通道（Microchannel，MC）[3]、核磁共振（Nuclear magnetic resonance，NMR）[38]和计算机断层扫描（Computed tomography，CT）[38]等. 本部分主要介绍这些纳微米实验测量仪器及技术在解决一维（1D）、二维（2D）和三维（3D）多孔介质细观流动方面的应用进展（图 2）.

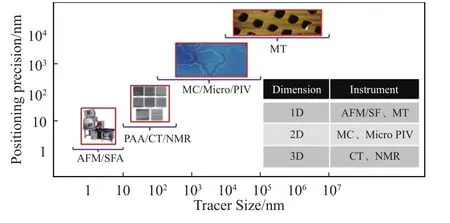
图2 不同“微测量仪器”的尺度范围Fig.2 Scale range of different “micro-measuring apparatus”

李战华与郑旭[30]认为目前细观流体流动测量仍然沿着经典流体力学测量“小型化”的思路开展. 石英微圆管（管径d=10 μm～10 mm）作为一种研究一维微流动问题的实验材料进入研究人员的视野. 王渝明等[39]研究了N2在微管中的流动规律，微尺度效应越显著实验流量越偏离达西理论流量，非线性流动特征也越明显；Jerauld与Salter[40]、McDougall与Sorbie[41]研究并计算了润湿性对水驱油效果的影响，并绘制了油水相对渗透率曲线； Bonaccurso等[35]利用AFM研究了不同粗糙度硅片在去离子水中的边界滑移特性；这些实验多是通过对微流体一维尺度流动的研究来寻找流体微尺度效应的判断参数和临界值等. 随着“芯片实验室”的出现使得细观流动的研究由一维流动升级到了二维流动，如Wang等[42]研发了一种控制微通道内压力驱动多相流界面位置的新设备，并为解决微通道内两流体流动的非匹配黏性问题提供了一种新的方法. MC与Micro/Nano PIV等结合后尺度范围（100 nm～1 μm）更为广泛且逐步实现了三维流动问题的研究，Ou与Rothstein[37]利用PIV测量了采用光刻技术加工的具有表面微结构的超疏水硅片表面的边界滑移长度；Datta 等[43]使用共焦显微镜（Focused ion beams and scanning electron microscopy，FIB-SEM）直接观察三维多孔介质中非湿润流体的形成和复杂形态. Arif等[44]认为要想完整描述页岩微观结构，需要跨多个尺度.

1.3 数值模拟

孔隙网络模型（Pore network model，PNM）是一种利用计算机技术并结合图像处理学、拓扑学、几何学等，在微观尺度下进行多孔介质的微观网络构建、孔喉仿真模拟和分子间作用描述，且能够较为真实地反映复杂的多孔介质微观流动规律的方法[45]. 本部分主要介绍分子动力学模拟（MD）、格子玻尔兹曼方法（LBM）模拟和孔隙网络模型（PNM）的构建及其在微流动仿真模拟中的应用，通过成像技术（Micro CT、NMR和FIBSEM等）获取多孔介质的基本孔隙特征，并按照模型构造方法利用计算机模拟软件（MS、Fluent、Comsol和CFD-ACE等）完成构建并进行仿真模拟（图 3）[5,23].

图3 孔隙网络模型及应用软件分类[27, 46]Fig.3 Pore network model and application software classification[27, 46]

1956年Fatt[47]研究毛管压力特征时首次引入网络模型，Dullien等[48]对他的研究进行了补充和完善. 此后，国外许多学者对多孔介质网络模型的构建和应用作了大量工作，目前已被广泛应用于模拟各种不同的流动过程，包括相交换、化学反应输运、非牛顿驱替和非达西流等[21,49-50]. Ju等[5]建立了二维细观尺度多组分LBM水驱油模型，并比较了不可压缩流体密度比对两相驱替的影响.Xie等[51]对润湿黏弹性流体进行了LBM建模，并研究了3种不同的孔隙几何结构中液滴的运移、捕获等. Cai等[22]利用MD模拟得到的单缝模型孔隙中的输运扩散系数计算有效扩散系数. 王金勋等[52]利用PNM研究了水驱油两相渗流规律，计算了非稳态法油水相对渗透率曲线和气液体系渗吸过程的相对渗透率. Wang等[23]为了预测页岩表观渗透率，将MD和PNM相结合，建立了一个多尺度的页岩气渗流模型. 目前研究的网络模型大多为准静态网络模型，考虑了毛管力的作用，忽略了各种微观力的影响，也没考虑岩石骨架与流体之间的界面作用，更无法真实地反映微观尺度下流体的流动机制.

2 细观尺度下流体流动的主要特征

随着多孔介质中流体流动过程中的孔隙特征、界面效应及尺度问题等越来越复杂，研究人员更加关注细观尺度下多尺度效应、微可压缩性、界面效应和微观力作用等所带来的变化，特别是在油气渗流、多孔介质材料科学和纳米科学等领域. 本部分将对细观尺度下流体流动的几个主要特征作详细论述.

2.1 多尺度效应

目前对于单一尺度下流体流动的研究已经相对成熟，然而对于分子尺度微观作用方面的研究尚不完善. 多尺度效应(细观-宏观)是在探寻流动过程中小尺度对大尺度的影响规律，完成宏观性能预测或通过微观结构设计改进材料性能所必须要考虑的主要因素之一[53].

本文主要针对现代油气渗流过程中的多尺度问题进行评述. 对于油气储层而言，其非均质性尤为显著，特别是当前研究的热点— —非常规储层渗流过程存明显的多尺度特性. 从多尺度划分上看，现代油气渗流过程横跨细观尺度和宏观尺度，在不同尺度上具有不同的渗流模型，如表1所示.宏观尺度的油气藏渗流主要以达西流和自由流为主，而对于细观尺度而言，其油气渗流呈现明显非线性规律，达西定律不再适用；于是研究人员针对不同尺度多孔介质的渗流模型做了大量的实验和理论上的修正，目的是以满足当前非常规油气藏的开发需求. 针对非常规油气藏，马勇军与王瑞飞[54]、马铨峥等[55]、邓佳[56]也针对不同非常规油气藏的特点构建了相应的渗流模型；而对于低渗透油藏(细观尺度)，黄延章[57]、姚约东与葛家理[58]、杨清立等[59]、邓英尔与刘慈群[60]、以及黄延章等[61]建立了大量分段模型和连续模型.

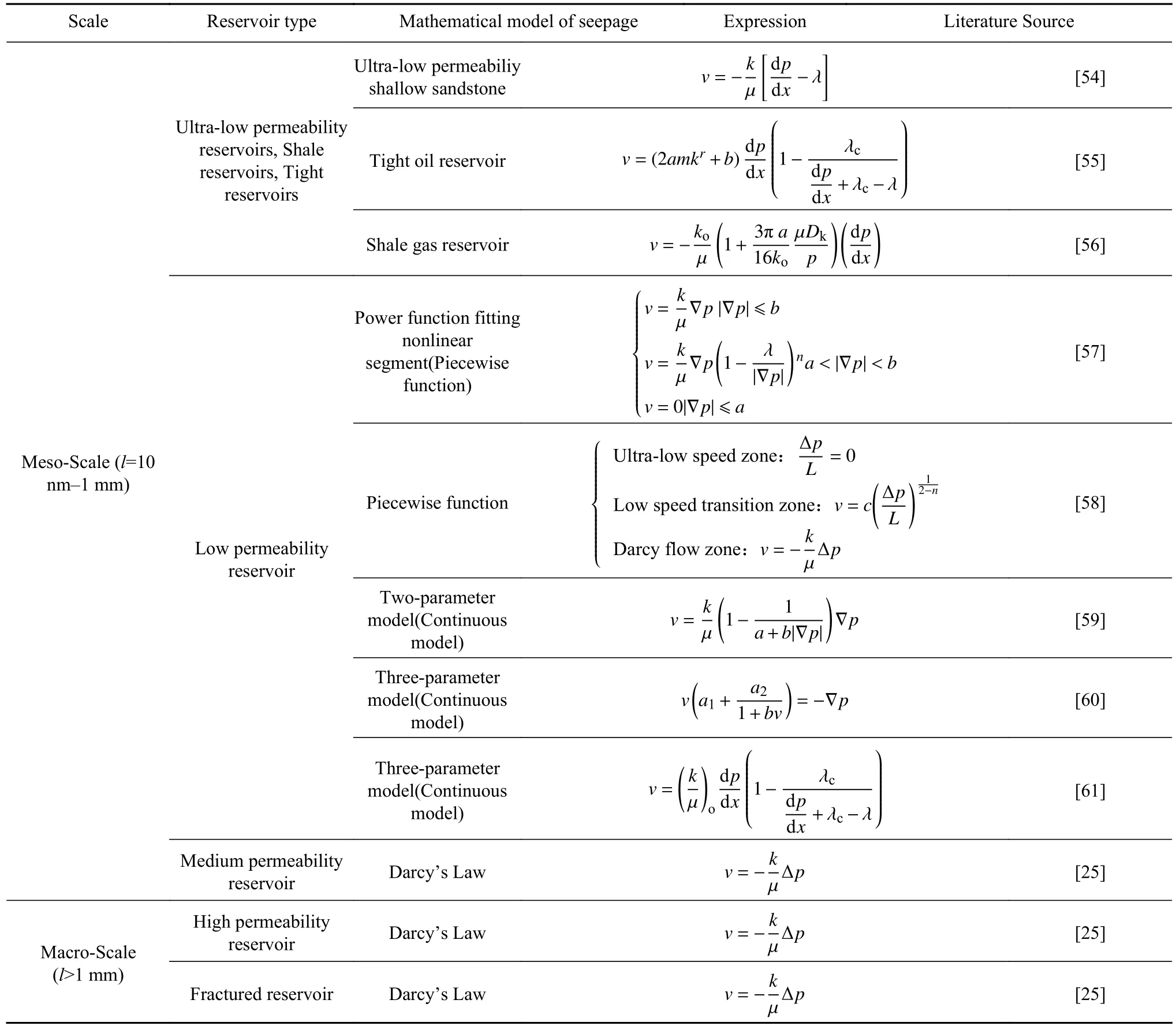
表1 不同尺度油气渗流数学模型Table 1 Mathematical models of oil and gas seepage in different scales

目前非常规油气藏由于压裂技术的广泛应用，尺度范围跨越宽，其多孔介质流动问题更加复杂(主裂缝-微裂缝-基质)，因此对多尺度效应对于流动影响的研究尤为重要. 同时，笔者在研究非常规油气渗流问题时提出了“三大区，五小区”的多尺度描述方法来进行产能模型的研究，如图4所示[8].

图4 “三大区，五小区”多尺度模型[8]Fig.4 Multi-scale model of the “three large zones, five small zones”[8]

2.2 微可压缩性

流体的微可压缩性在很多应用领域广泛存在，如液体在微小多孔介质内的流动[62]，液体的微可压缩性在高压低速条件下变得重要，尤其是在细观尺度下. 液体流体在细观尺度流动时，流速明显低于同尺度下的泊肃叶流速，那是因为我们往往忽略了微可压缩性，但在细观尺度油气渗流中，地层压力大，液体流体表现出较为明显的微可压缩性. 本部分主要针对液体流体的微可压缩性对细观尺度油气渗流的影响展开评述.

油气渗流属于高压低速流（低马赫数流），对其进行数值模拟的手段一般会针对是否忽略密度的微小变化展开讨论，因为其微小密度变化是否可以被忽略，是由所研究问题是否需要涉及流体的微可压缩性所决定的. 向大平等在2002年前后提出并验证了一种低马赫数流动数值模拟方法——微可压缩模型(Slightly compressible model：SCM)[63-64].对于微可压缩流体的流变学模型，我们可以根据最基本的流变学模型（马克斯威尔模型（Maxwell）、开尔文模型（Kelvin）以及宾汉模型（Bingham)）进行适当的选择并进行修改[49,65-66]. 张雪龄等[34]、栗雪娟等[67]、Venerus[68]针对微可压缩黏性流体进行了详细研究，采用正则摄动法求得摄动解，发现压降和阻力系数明显偏离了不可压缩流体. 到目前为止对微可压缩流体的数学模型的研究发现它可以提高低马赫数流动计算精度，且对于定常计算其残差能够收敛到零[69-70]. 笔者团队张雪龄博士[71]对圆管中的单相和两相微可压缩流体的不稳定流动进行了详细研究，建立了非稳态流动数学模型，分析了单相和两相流动规律，发现微可压缩性对流体的微尺度效应影响显著，并给出了微圆管中流体流动的“临界启动尺度”，对多孔介质细观流动中的微可压缩性对油气渗流机理的影响有了更加全面的认识.

2.3 界面效应与微观力作用

在以往的油气渗流力学研究中，通常只需描述常规多孔介质中的油气渗流规律，所以其流动行为可通过达西定律（或泊肃叶定律）进行描述，许多微观作用机理如流体界面效应和微观力作用等均不起主要作用，因此可以忽略. 然而，非常规油气藏的孔隙结构往往非常小，流体受界面效应和分子间微观作用力的影响将越来越明显，呈现出不同于宏观尺度下统计规律的特性，从而导致牛顿流体也呈现出非牛顿流体的性质，极大的表面积/体积比值还导致了分子间作用力（范德华力）、电黏性效应、空间位形力和流体在固壁产生的界面效应等. 使用传统的达西定律或泊肃叶定律已不能准确描述这些微观因素，如Liu与Li[72]采用兰纳-琼斯势 (Lennard-Jones potential) 表征了流体分子与壁面的范德华力作用，并发现流体在纳米多孔介质中流动时N-S方程将不再准确；Yang与Li[73]发现受双电层影响的流体流速明显偏离了泊肃叶流；另外，朱维耀等[74]建立了考虑聚合物软颗粒在通过微通道时的空间位形力作用的微圆管渗流模型. 在非常规油气开发的大背景下，宏观流动规律与理论不能准确描述并解决细观尺度多孔介质中的流体流动问题已成为当下现场实际生产中所面临的重要窘境. 因此有必要对细观尺度中的非线性流动进行研究，并建立新的研究方法，解决细观尺度下多孔介质中流体流动的界面效应、微观力作用规律和非线性流动等问题. 本课题组通过纳微米管等设计实验[75]和细观力学理论[76]，分析了纳微米管界面特性与界面力作用关系及其与流体流动特性的关系，进行纳微米管界面与流体特性参数表征，搞清网络结构性能对单相、两相流体特性的影响关系，阐明介质结构尺度、流动界面、流体相、微观力等特性关系.

3 多孔介质中流体流动仿真模拟

非常规油气资源开发正在如火如荼的进行当中，其中对于细观尺度的岩石孔隙结构中油气的赋存状态和流动规律的研究尤为重要，而“孔隙网络模型”[47]的诞生为解决和完善细观多孔介质中的流动理论提供了一种行之有效的方法. 近20年来，油气开发领域的大量国内外专家学者利用该方法来研究非常规油气在细观尺度多孔介质中的流动问题，它能够在一定程度上还原真实岩心的孔隙空间特征，如果再通过室内实验手段人为赋予其相应油气渗流参数，就可以模拟计算或定量预测细观尺度孔隙结构中的油气渗流规律.

3.1 岩心孔隙网络重构技术的发展

目前岩心孔隙网络模型重构方法主要是物理方法和数值方法，物理方法都是借助CT、SEM等高精度仪器获取岩心内部结构从而对其进行重构；数值方法先根据岩心图像获取必要的信息，之后建立数字岩心Hazlett[77]和Coles等[78]根据超薄切片法以及相关函数构建出了三维数据场，利用CT、NMR等技术实现多孔介质三维孔隙空间图像再现技术. Joshi首次提出了利用统计方法重建岩石孔隙空间[79]，Quiblier在Joshi的算法基础上，进一步发展了非线性算法，建立了三维孔隙空间[80]. 但后来研究人员发现对于只使用孔隙度等不能准确描述多孔介质的微观孔隙结构，于是又引入了一些新的约束条件，如孔隙通道长度、孔喉信息等[81].也有研究人员采用模拟退火的方法来进行岩心重构工作，该方法计算过程复杂，仅仅使用在组分较为简单的岩石孔隙中[82-84]. 随后，马尔科夫链-蒙特卡洛法(MCMC)被Wu等研究人员应用于研究土壤结构，并拓展到了三维数值岩心的重构，后经一些学者的研究发现MCMC法可以精度较高地完成均质岩心孔隙结构的重构工作[85]. 纵观岩心孔隙结构重构技术的发展，目前对于岩心孔隙结构的重构技术的研究任重而道远，而应用相对成熟的孔隙网络模型的方法来研究细观多孔介质中的流动问题更加便捷、准确.

3.2 考虑微观力作用的孔隙网络模拟

微观网络模型可以作为微观尺度下描述分子之间作用特性的一种仿真模拟手段，可以与室内实验结果高度配合，是研究孔隙介质中微观作用的一种有效手段. 早在2000年胡雪涛与李允[86]就采用定向渗流理论完成了可以简单模拟微观剩余油分布的随机网络模型的构建工作. Blunt等[87]建立可以描述多孔介质中多相流润湿性的孔隙网络模型，并简单完成了Berea砂岩中油水相对渗透率的预测工作. 徐守余与李红南[88]等研究了储集层喉道网络场的变化和对剩余油的影响情况. 随后，王克文等[89]利用孔隙网络模型研究了聚驱后不同孔隙结构中剩余油的分布情况. 姚军等[90]建立了由孔隙-喉道组成的三维网络模型，完成了对毛细管压力和相对渗透率的求解模型. 张鹏伟与胡黎明[91]考虑岩石孔隙特征参数建立了等效孔隙网络模型. 目前，对于细观孔隙中的微观力作用对流体流动影响的研究，难以真实反映流体在多孔介质中的流动. 为了更加准确地刻画细观尺度下孔隙中流动问题，笔者建立了考虑微观力作用的油水两相网络仿真模型，并计算归纳了孔喉特征及压力特征等因素对含水率及相对渗透率的影响规律，进一步明确了细观孔隙中流体流动的力学特性. 然而，目前的网络仿真研究的模型规模太小，最大规模也仅在毫米级（小于5 mm），与岩心的厘米级尺度相差很大，难以与岩心实验进行对比研究，不能归纳总结纳微米孔隙中的流动规律. 有必要进一步扩大网络模型的规模，使实验和模拟结合进行研究. 为此，需要开展细观层面上的纳微米尺度流动实验、理论及模拟研究，进一步提高实验手段和技术，搞清流体在分子间微观作用力的影响下的流动机理，形成微尺度下的流动模型，并以此为基础，构建考虑微观作用力的大规模计算机仿真模型，与实验结果相互验证，分析微观尺度流体流动机制以及提高采收率方法尤为重要.

4 多孔介质中的流体动力学机制

石油领域的相关学者在研究细观尺度岩石孔隙中的流体流动时发现，油水两相流体在孔隙喉道中的流动受到各种力的作用，其相互之间的力学机制相当复杂；如果从宏观和微观的角度出发，多孔介质中水驱替原油过程中的力学关系可以分为宏观力和微观力两大类. 本部分主要介绍了细观尺度下油水流动动力学机制的研究现状及发展方向.

4.1 多孔介质中剩余油形成机制

针对页岩等非常规储层多孔介质中剩余油形成问题，主要需要解决的是细观尺度岩石孔隙中的油水分布及流动状态. Pak等[38]利用CT成像技术，定量可视化地分析了在低、高毛管数下注入润湿相（盐水）后，对高非均质性碳酸盐岩中的非润湿相（油）的原位结构进行表征. 闫伟超与孙建孟[92]探讨了各种物理实验技术和数值模拟方法在剩余油研究中应用的优缺点. 王芳芳等[93]对剩余油的赋存状态进行了重新划分. 目前针对剩余油研究多以直接观察为主，但对于其形成机制的定量研究较少. 笔者通过开展多孔介质细观动力学研究，建立了考虑固液分子作用、粗糙度影响的微圆管单相和两相流体流动动力学数学模型，揭示了流体在微通道内的流动规律[31,34]；根据建立的微圆管流动数学模型[76]，依据质量守恒定律，建立了水驱动态网络结构数学模型，该模型不同于准静态网络模型，不仅考虑了黏滞力与毛管力的作用，同时还考虑了岩石骨架与流体之间界面作用对流动规律的影响，并编程实现了多孔介质中水驱油动态网络模拟，获取了水驱油时孔隙节点的压力变化以及网络模型的剩余油分布[9,21,94]；同时建立了固液分子作用下的聚合物驱油动态网络模型，如图5所示[74]，模拟研究了聚合物浓度、相对分子量、吸附层厚度及固液分子作用对剩余油分布的影响，揭示了聚合物驱油机理，为研究剩余油成因机制及挖潜剩余油奠定了理论基[49].

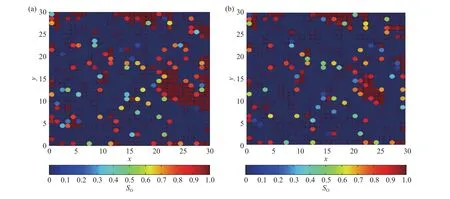
图5 水驱和聚驱后剩余油饱和度(So)二维分布情况. （a）水驱后；（b）聚驱后[74]Fig.5 Two-dimensional distribution of remaining oil saturation: (a) after water flooding; (b) after polymer flooding[74]

4.2 仿真模拟与室内模拟验证

在油气开发领域，由于地质储层埋藏深度高，相关学者对于油气在岩石储层中的存在及流动的细观规律研究较为困难. 随着1952年“夹珠模型”的出现，掀起了众多研究人员对于孔隙介质中流体流动规律的研究热潮[95-96]. 随后应运而生了很多研究细观油气渗流机理的方法和手段，如填砂管模型、大型平面胶铸模型和仿真树脂模型等物理模拟实验[97]. 笔者团队曾利用微圆管分析去离子水和煤油的实验流速、有效界面层厚度与压力梯度的关系，考察壁面润湿性和流体黏度对细观流动规律的影响. 另外笔者团队为观测低渗透储层内微观渗流动态及探索流体细观流动机理，在前人的基础上，对可视化网络仿真技术进行了大量的优化改进，给出一种模拟二维多孔介质可视化渗流模型的制作方法，并以此为基础进行了大量的细观多孔介质中流体流动动力学机制的研究工作，从实验研究到理论模型分析建立了一套完整的研究体系[3,8-10,19,74,98]. 但是非常规油气资源开发的兴起将流动的尺度进一步拉低到了l=10 nm～1 μm的尺度范围，所以需要进一步研发“小尺度”的微流动装置，如Shen等[36]利用纳米阵列氧化铝膜（l=10 nm～1 μm），进行了气驱水实验和单相气体流动实验，并分析了纳米尺度下气驱水流动特征；总体来说，如何寻找并实现二维、三维仿真多孔介质模型用来研究细观尺度流动机制，是未来研究的重点方向.

5 结论与展望

对于细观尺度下多孔介质中流体流动理论的研究，由线性渗流理论向物理化学、非牛顿、多尺度非线性渗流发展，特别是在非常规油气资源开发过程中，储层孔隙大多为纳微米级别，其流动过程中受到界面及微观力作用明显，为了解决非常规油气开发储层渗流阻力大、开采难、剩余储量难以动用的难题，使我国油气研究和开发方面达到国际领先水平，进一步提高我国非常规油气藏的开发水平. 笔者认为目前针对多孔介质细观流动的研究，在继承前人研究结论认识的基础上，应该紧紧围绕微观力学和渗流力学等方面进一步深化研究.

（1）通过细观动力学理论分析及实验研究，详细分析微观力的作用范围和受控因素，搞清微观各种力的相互作用关系及对驱动的影响. 利用微纳米圆管、碳纳米管、微观仿真模型流体流动精细实验研究微尺度效应，通过微测量技术，进行速度、浓度、压力梯度的微测量. 利用致密（微纳米级孔隙）岩心、含微裂缝岩心、裂隙介质岩心、含裂隙特点岩心进行渗流物理模拟，进行二维、三维渗流物理模拟实验，研究不同条件和尺度下的渗流规律和流场分布规律，揭示细观作用力作用，搞清流动阻力控制因素及影响规律.

（2）非常规油气藏一般使用多级压裂的方法来开发，这就使得非常规储层中的多孔介质变得尤为复杂，其中包括裂缝，微裂缝和基质等多尺度问题以及界面效应与各种微观力的作用，那么在开发过程中流体的渗流规律就会变得更加复杂.因此，基于纳微米尺度流体流动界面作用与细观力学特性关系，阐明油水细观流动动力学机制，揭示多孔介质中复杂流动的细观流动机理，实现细观与宏观尺度动力学关系数学描述，解决纳微米孔隙流体流动特性问题，推动非线性渗流和细观渗流力学的发展尤为重要.

（3）利用岩心CT扫描等现代化有段获取非常规储层岩心样本数据，考虑配位数、孔喉比、孔径分布等孔隙结构参数及模型润湿性等特性，编写新的仿真方法，将三维网络模型的规模由以往的毫米级扩展到岩心级，建立了考虑控制方程的纳微米尺度两相细观流动数学模型，并进行油/水、气/水两相驱替微观模拟，定量分析油气分布规律和尺度效应作用机理，研究细观尺度下压力分布及驱替规律等，为提高驱替效率的进一步研发提供基础.