基于磁记忆检测的桥钢箱梁翼缘损伤状态力磁关系

苏三庆，秦彦龙，王 威，左付亮，邓瑞泽，刘馨为

西安建筑科技大学土木工程学院，西安 710055

钢箱梁因其轻质高强、塑性好，且箱形截面具有较大的抗弯刚度和较强的抗扭性能，具有较大跨越能力，能很好的承受横向分布荷载，适用于各种复杂结构而在桥梁结构中被广泛应用[1]. 但在桥钢梁使用过程中，由于内部裂纹和外界环境以及自然灾害的原因，会产生截面或节点的刚度、强度的退化及变形等损伤[2]. 在一定情况下会引起结构的失效，造成严重的安全问题，这就使得对在役桥梁钢结构的检测成为必需.

金属磁记忆检测技术是一种新兴的磁无损检测方法，这种检测方法可对铁磁构件应力集中区域及存在隐性损伤的部位进行早期发现和识别，并采取有效的预防措施，防止铁磁构件的突然破坏，有早期预警的作用[3-4]. 其基本原理是铁磁性材料具有磁畴结构和自发磁化的特征，在外加磁场和应力的作用下，铁磁材料内部将发生磁畴壁移动和磁矩转动，在构件表面出现磁场强度的改变，损伤区域产生自有漏磁场，并且存在“记忆”现象[5-6].

金属磁记忆检测技术由于操作简单、灵敏度高，已经被应用到了轨道、管道、压力容器，飞机起落架等铁磁性构件安全检测当中[7]. 目前，国内外众多学者对金属磁记忆检测技术进行了大量的理论研究和试验研究工作[8]，相关学者对漏磁信号与应力状态之间的关系展开了细致的研究，用来建立构件表面或内部损伤与磁信号的关系[9]. 文献[10]进行了再制造业磁记忆检测技术研究的探讨. 文献[11-12]研究了钢丝绳磁记忆检测技术的力磁关系. 文献[13-14]对磁记忆检测技术在建筑钢结构领域的应用进行了初步研究. 文献[15-16]对简单构件进行了有限元模拟计算. 但以前研究大多属于桥梁等建筑结构以外其他领域的构件，多以简单受力为主，在桥梁钢结构方面磁记忆检测技术的研究尚处于探索阶段.

因此，选用波纹腹板钢箱梁进行基于磁记忆检测技术的力磁关系试验研究，以探索用磁信号来检测和预警桥钢箱梁的损伤. 本文通过对桥钢箱梁进行4点受弯的静力加载试验，发现其在上翼缘发生屈曲失稳破坏，得到了钢梁表面的漏磁场信号曲线及漏磁场梯度曲线，由于钢箱梁在受力过程中翼缘和腹板的受力情况不同，所产生的磁信号变化也不同，所以本次重点讨论上翼缘磁信号变化情况. 结合有限元计算的应力分布情况，给出了应力与磁信号之间的关系曲线；提出了用磁场梯度指数作为参数对损伤进行检测和预警.

1 试验过程及结果

1.1 试验材料及方法

选用具有代表性的 Q345qC桥梁钢材进行基于磁记忆检测的受弯试验研究，Q345qC 钢材具有良好的力学性能、焊接性能及低温变形能力，在桥梁钢方面应用最为广泛. 材料的化学成分及力学性能分别如表1和表2所示.

表1 Q345qC 钢材化学成分（质量分数）Table 1 Q345qC steel chemical composition %

表2 Q345qC钢材的力学参数Table 2 Mechanical parameters of Q345qC steel

试件三维模型如图1所示，腹板尺寸由桥梁钢箱梁常用1000 型波纹腹板进行 1/4 缩尺而来，横截面尺寸如图2所示. 本次实验采用两个钢箱梁试件，钢梁加载时支座处外伸150 mm，钢梁有效长度l分别为1800 mm和1500 mm，横截面尺寸相同，下文中对钢梁的描述均采用有效长度. 波纹腹板钢箱梁4点受弯试验在YAJ20000型电液伺服压剪试验机上进行，其最大试验力为20000 kN. 试件表面的磁记忆信号采集设备采用EMS-2003智能磁记忆/涡流检测仪. 检测探头采用磁记忆双通道笔式探头，探头编号为EPMS/B2，其分辨率为1 A·m-1，量程为±1000 A·m-1.

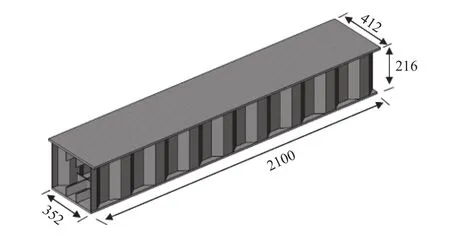
图1 试件三维图（单位：mm）Fig.1 Three-dimensional model of specimen (unit: mm)

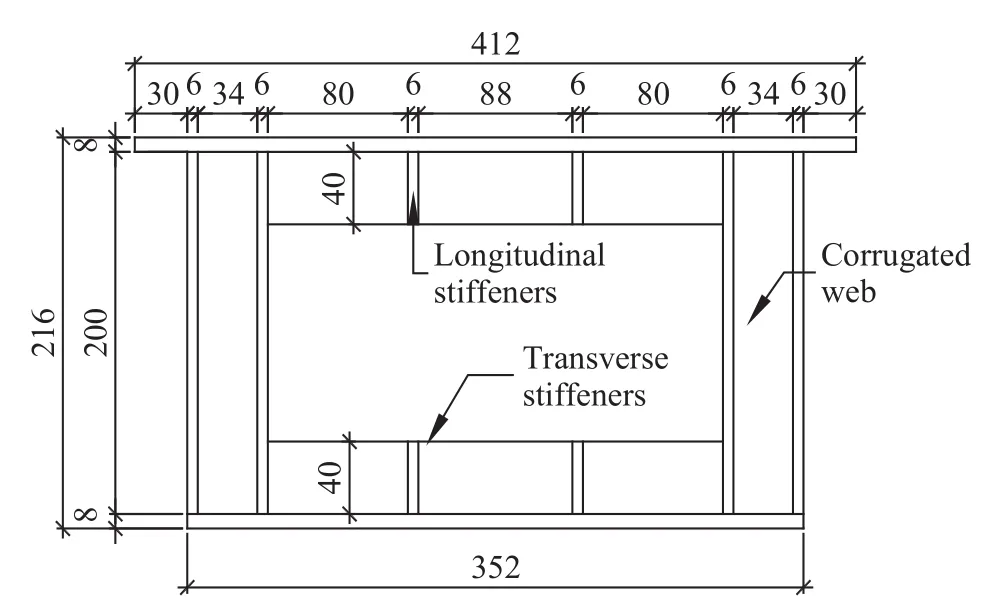
图2 试件横截面图（单位：mm）Fig.2 Cross section of specimen (unit: mm)

试验中4点受弯加载方式如图3所示，P代表YAJ20000型电液伺服压剪试验机的集中荷载作用力. 磁信号采用保载在线测量的方式，测线沿钢梁长度方向布置，检测步距为50 mm，上翼缘检测线布置位置如图4所示. 磁记忆检测试验中由于需要测量每个阶段的磁信号，故钢梁试验前先由材性试验得到精确的本构模型（应力–应变（σ–ε）曲线）如图5所示，试验前计算得到1800 mm长钢梁屈服荷载为900 kN，设置加载等级为0、200、400、600、800、900、1000、1050和1100 kN. 1500 mm 长钢梁屈服荷载为1000 kN，设置加载等级为0、200、400、600、800、900、1000、1050和 1123 kN. 测量时将传感器垂直并紧贴试件表面，以消除提离值的影响，保证在检测过程中提离值保持为零. 为了保证结果的准确性，减少意外误差的影响，在每个测点收集了3组数据，丢弃与其他测点有显著差异的数据. 取其余的平均值，得到比较准确的结果.

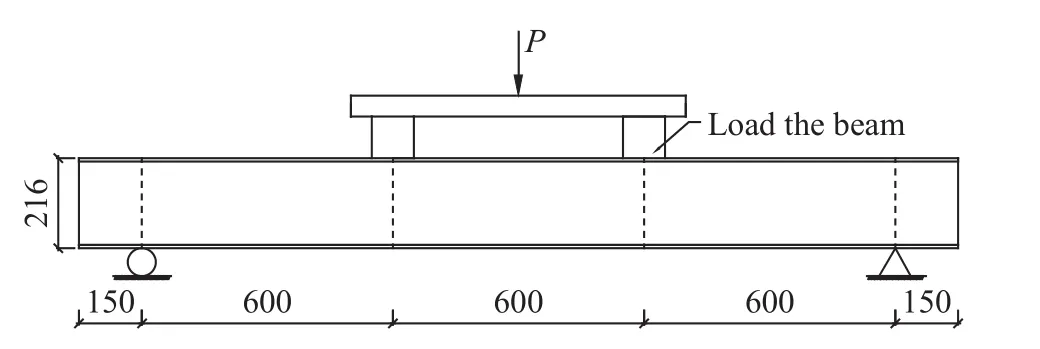
图3 试件加载示意图（单位：mm）Fig.3 Specimen loading mode (unit: mm)

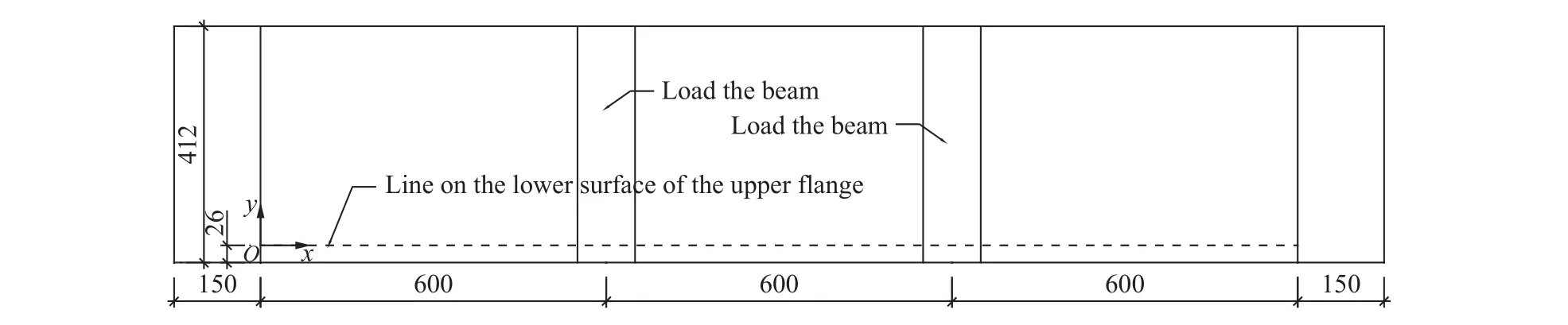
图4 上翼缘检测线布置示意图 （单位：mm）Fig.4 Upper flange detection line layout (unit: mm)

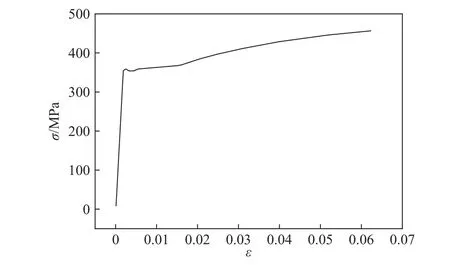
图5 试件本构模型曲线Fig.5 Constitutive model curve of the specimen

1.2 试验结果

试件加载至最终失去承载力的状态如图6所示，两个钢箱梁破坏情况一致，都为上翼缘屈曲损伤，且最大损伤区域发生在加载点附近，因此本文重点研究上翼缘损伤部分的力磁关系. 钢梁上翼缘以压应力为主，上翼缘应力沿垂直于宽度方向的截面上变化相同，故在只考虑应力引起磁信号变化的时候，沿垂直于宽度方向的截面上磁信号变化也相似，所以这里选用一条沿钢梁长度方向检测线上的磁信号来分析钢梁上翼缘损伤变化情况. 1800 mm的钢梁加载过程中荷载位移曲线如图7所示，其中屈服荷载Fy为900 kN，极限承载力Fu为1100 kN，对应的屈服位移Δy为18.2 mm，极限位移Δu为41.5 mm.

图6 试件最终破坏形态Fig.6 Final failure pattern of the specimen

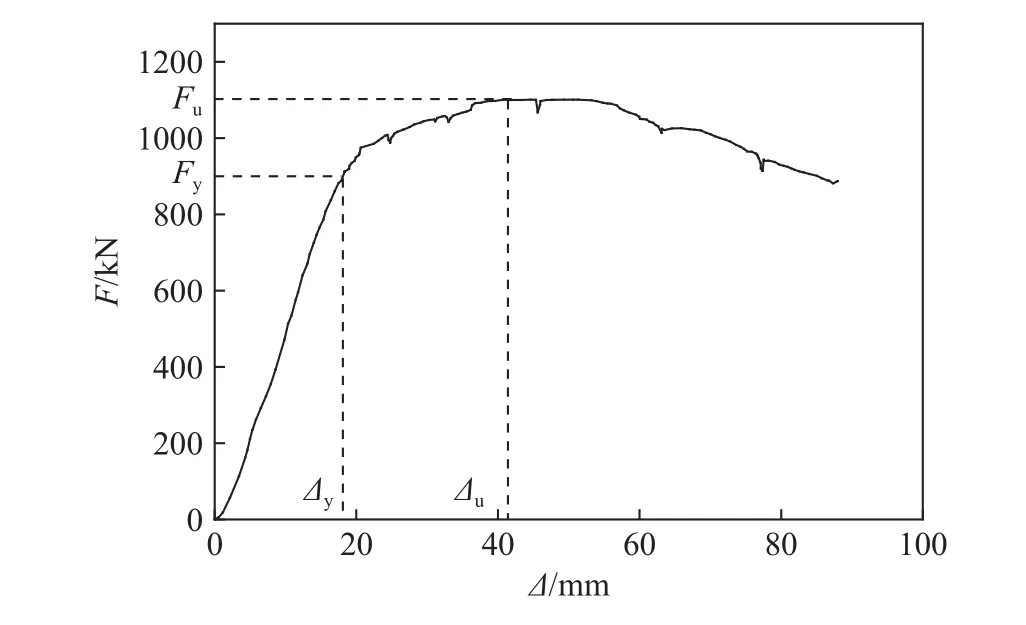
图7 1800 mm钢梁荷载位移曲线Fig.7 Load displacement curve of the 1800 mm steel beam

1.2.1 磁信号曲线分布

读取上翼缘各加载阶段磁信号数据，做出初始阶段变化曲线如图8所示. 初始阶段磁信号波动较大，这是因为试件内部磁畴未受到应力的约束，处于无序的分布状态. 由于金属的多种内耗效应，试件内部将出现不同程度的磁化，且钢材在制造过程中杂质和缺陷会导致材料局部的磁导率下降，形成高磁阻区，阻碍磁力线的通过，在这些缺陷区域内形成不均匀的磁势差，使原本均匀的磁力线出现畸变，从而在试件表面产生不等的自有漏磁场[17-18]. 但初始磁信号曲线仍然大体上呈现左右对称，磁信号曲线在加载点处出现峰值，且右侧加载点处的峰值明显大于左侧加载点处，初始状态磁信号的变化表明了钢箱梁初始的磁场状态.

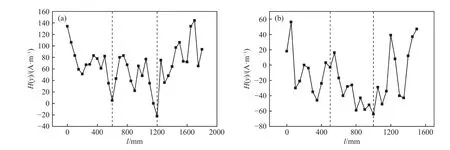
图8 钢梁上翼缘初始磁信号变化曲线. （a）1800 mm 钢梁；（b）1500 mm 钢梁Fig.8 Curves of the initial magnetic signal of the upper flange of a steel beams: (a) 1800 mm steel beam; (b) 1500 mm steel beam

钢箱梁加载过程中磁信号的变化如图9和图10所示，两个钢梁的磁信号变化趋势一致. 弹性阶段，在应力的作用下，磁信号呈现一定的发展规律，磁信号曲线呈现左右对称，在两个加载点处出现过零点现象. 磁信号数值整体为正，在中间1/3区域磁信号随着应力的增大而减小，两边区域磁信号随应力的增大而增大. 试件处于弹性阶段时，在应力和地磁场共同作用下内部产生了很高的应力能，试件内部的位错聚集处磁畴壁必将发生不可逆的重新取向，随着应力的增大，试件内部逐渐达到磁饱和状态，磁信号的分布趋于稳定[19-20].

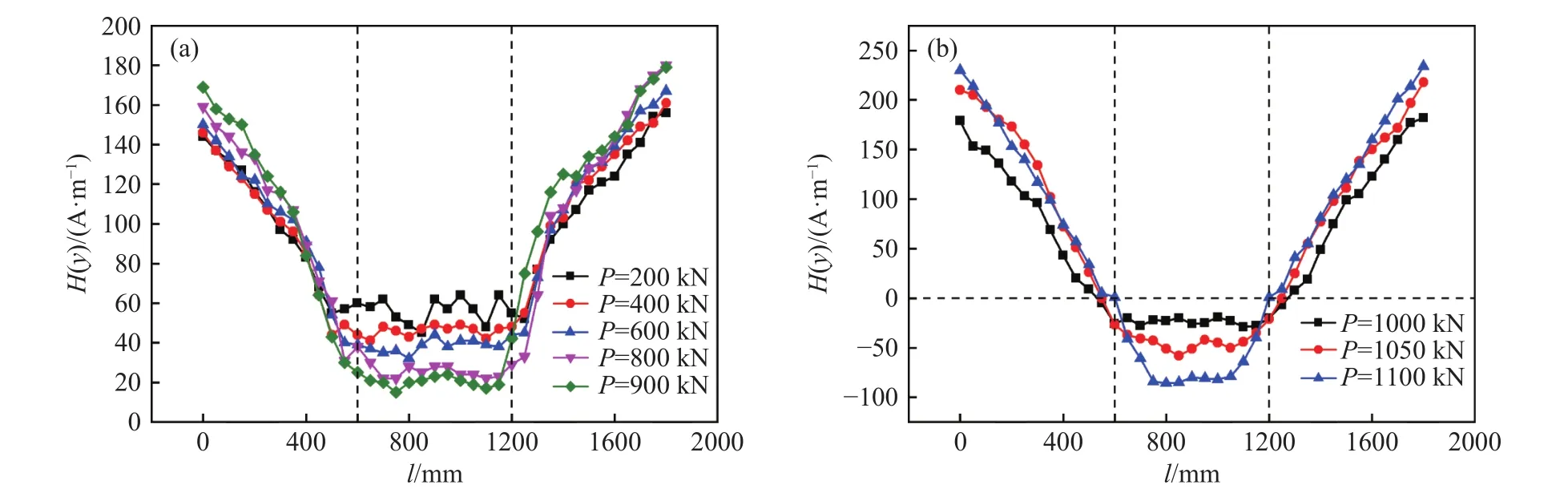
图9 1800 mm钢梁上翼缘加载中磁信号变化曲线. （a）弹性阶段；（b）塑性阶段Fig.9 Magnetic signal change curves during flange loading of the 1800 mm steel beam: (a) elastic stage; (b) plastic stage

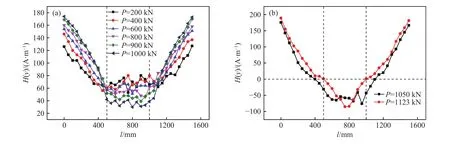
图10 1500 mm钢梁上翼缘加载中磁信号变化曲线. （a）弹性阶段；（b）塑性阶段Fig.10 Magnetic signal change curve during flange loading of the 1500 mm steel beam: (a) elastic stage; (b) plastic stage

塑性阶段，屈服后磁信号曲线立即向破坏后的状态靠拢，相比于弹性阶段，钢梁中间1/3区域，即纯弯段磁信号出现反转，由正值变为负值，磁信号随应力的增大向负方向增大显著. 其他区域和弹性阶段变化相似，且磁信号最大值不断增大，破坏时达到最大. 这是因为中间段为屈曲损伤区域，在钢梁屈服以后，应力作用下磁场已至饱和状态，试件内部磁畴重新取向已基本完成，磁畴壁的移动已达最大，最终向磁滞状态逼近，且塑性变形加速了位错密度的积累，位错对磁畴的钉扎作用阻碍了磁畴的有序化运动，并降低了磁化强度[21].

1.2.2 漏磁场梯度曲线分布

磁信号梯度值K可以反应磁信号变化的快慢程度. 根据磁偶极子模型，自由漏磁场反映的是磁荷密度的积分场，为了更好的建立应力σ与磁信号之间的量化关系，采用基于离散数据的中心差分算法对磁信号法向分量进行一阶微分，得到漏磁场梯度公式[22]如式（1）所示.

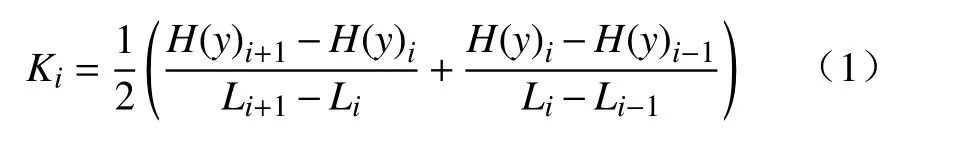
做出钢梁整体加载阶段漏磁场梯度曲线如图11和图12所示. 磁信号梯度曲线整体呈现中心对称图形，且随着应力的增大曲线关于对称点逆时针旋转，即曲线整体斜率不断增大. 试件中间1/3区域的梯度曲线在0点附近波动，加载点附近出现峰值现象. 且右侧加载点处的峰值波动大于左侧加载点处，这与试件应力最大位置以及破坏后屈曲最大的位置靠近加载点右侧相对应. 随着荷载的增大峰值点不断向中间区域移动，试件破坏之后峰值点完全处于中间1/3区域中.

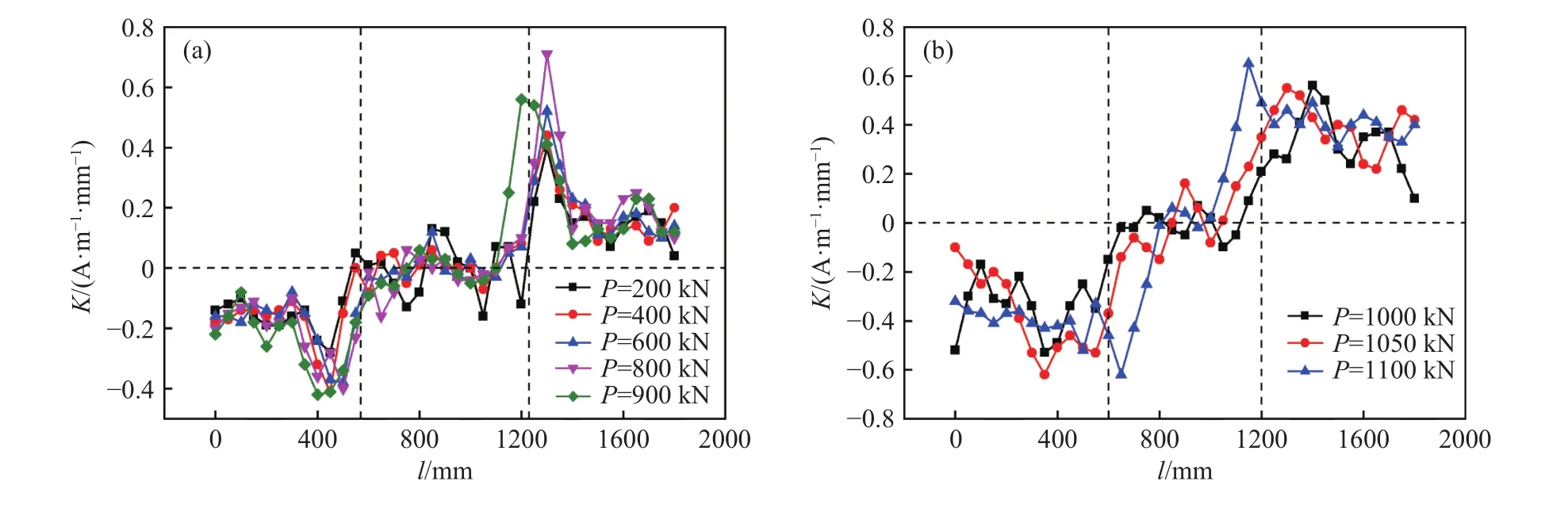
图11 1800 mm钢梁上翼缘磁信号梯度变化曲线. （a）弹性阶段；（b）塑性阶段Fig.11 Magnetic signal gradient curves of the upper flange of the 1800 mm steel beam: (a) elastic stage; (b) plastic stage

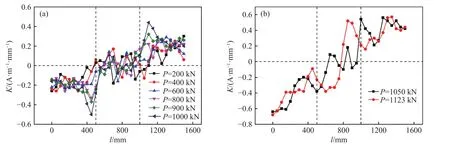
图12 1500 mm钢梁上翼缘磁信号梯度变化曲线. （a）弹性阶段；（b）塑性阶段Fig.12 Magnetic signal gradient curves of the upper flange of the 1500 mm steel beam: (a) elastic stage; (b) plastic stage

弹性阶段时磁信号梯度随加载等级线性变化，进入塑性阶段后，磁信号梯度数值增大显著，加载点处峰值对应的横坐标范围也明显扩大，这与试件应力发展正好一致，在弹性阶段应力线性增大，塑性阶段呈非线性变化，构件屈服后应力集中区域明显扩大，最终出现损伤. 由此可见，磁信号梯度曲线可以反映出钢梁整体应力变化情况，可以定性的说明构件损伤的位置及区域，以及损伤发展程度.

1.2.3 分析与讨论

Jiles等和Sablik等[23-24]认为，力–磁效应的物理本质是应力和磁场作用的等效性，即应力和磁场分别对铁磁材料中磁畴壁的作用是等效的. 根据J–A模型，应力对试件内部磁畴的作用可以看作一个附加的等效磁场，这个等效磁场如式（2）所示[25].

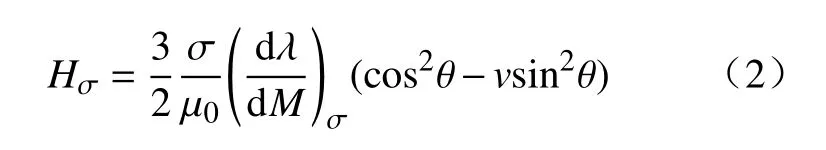
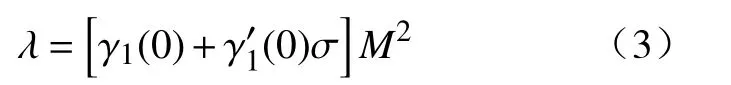
式中，根据试验数据可得[26]，

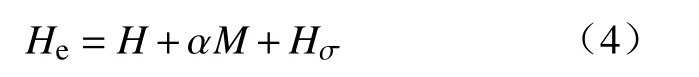
（1）磁信号在屈曲后转变为负值分析.

将式（2）和式（3）代入式（4）可得式（5）.

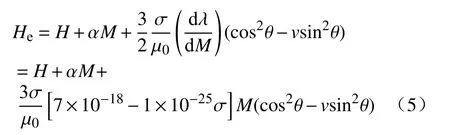
在本次试验中，地磁场强度H=40 A·m-1,材料按线性物质考虑，假定其磁化率为210，=0.001，则磁化强度M为8400 A·m-1. 由于等效场强度与应力方向有关，在外力加载作用下磁场的变化主要沿应力方向，因此可取[13]，则将钢梁进入塑性时的等效应力代入可得. 这与图9和图10中磁信号曲线进入塑性时转变为负值一致.

（2）磁信号梯度的分析.

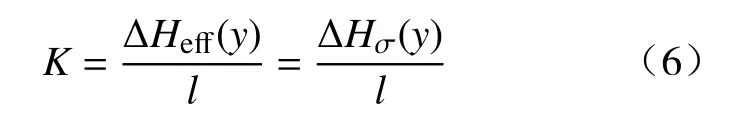
则等效应力场的表达式可表示为式（7）.

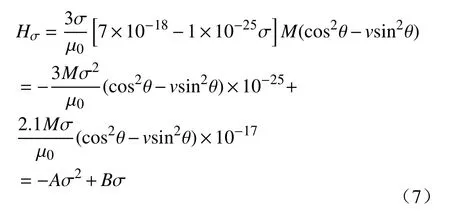
式中，当环境磁场不变时，A和B均可看成常量.

将式（7）代入式（6）可得磁信号梯度Ki的表达式为式（8）.

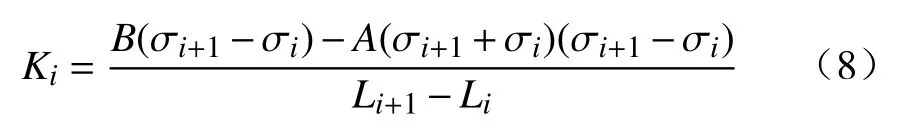
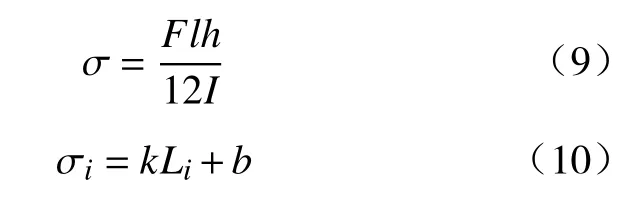
式中，k和b与荷载大小F和钢梁跨度l相关，k和b均为常数，h为钢梁截面高度，I为钢梁横截面惯性矩.

将式（9）和式（10）代入到式（8）中，可得到钢梁磁信号梯度值如式（11）.

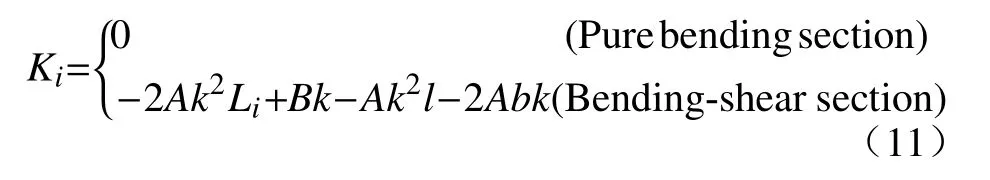
式中，对于每级固定荷载，A、B、k、b和l均可看作常数.

由式（11）可得，在纯弯段内，磁场梯度值K等于0，这就解释了翼缘纯弯段内梯度值在零值附近波动，近似为过零点的直线. 弯剪段内，磁场梯度值K是测点位置的线性函数，且斜率为负值，这也与磁信号梯度曲线有较好的一致性，但在弹性阶段梁端应力作用较小，磁场梯度值变化不明显，在塑性阶段明显的符合这一规律.

2 表征损伤的力磁关系分析

2.1 应力分布的有限元计算

磁记忆检测技术在结构中的应用在于建立应力与磁信号的关系，通过检测磁信号的变化来反映试件表面或内部的应力变化，从而对构件的损伤进行检测与预警. 为了得到试件精确的应力变化，建立力磁量化关系，采用有限元软件进行应力计算，采用的本构模型如图5所示. 由于两个梁的受力情况完全一样，故这里只给出1800 mm有限元计算的情况. 有限元计算的模型建立及网格划分如图13所示. 为了和试验对应，采用分级加载的方式，有限元计算的荷载位移曲线如图14所示，和试验对比误差较小. 钢梁翼缘以受正应力为主，腹板以切应力为主，为将复杂的应力等效为一个虚拟的单轴应力，采用Von Mises应力进行分析计算，钢梁受弯正应力和切应力云图如图15所示.

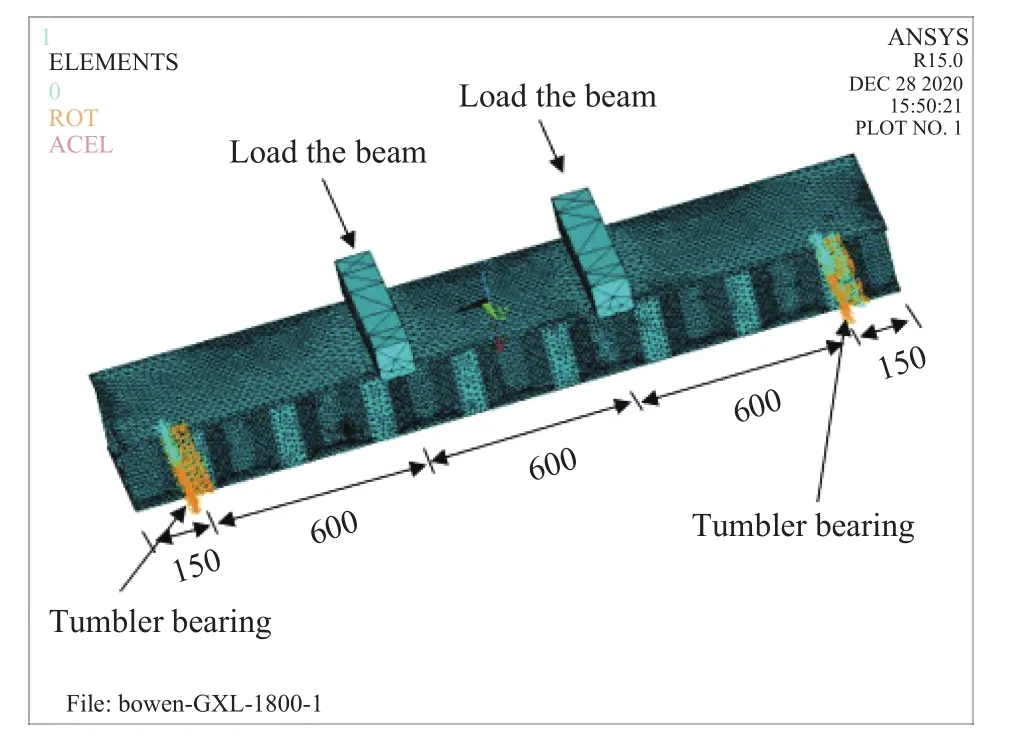
图13 有限元计算模型Fig.13 Finite element model

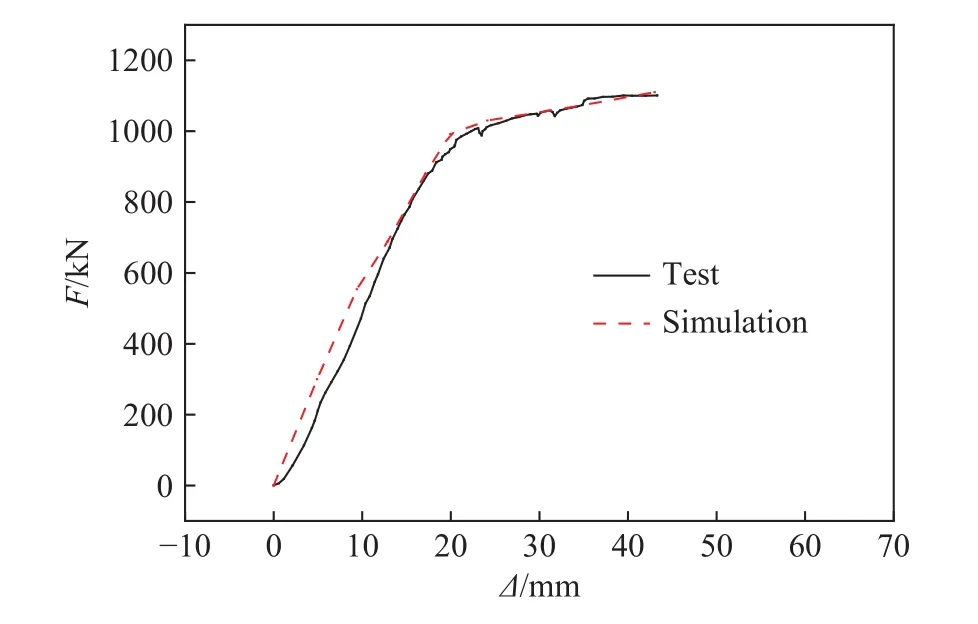
图14 有限元计算和试验的荷载位移曲线Fig.14 Finite element calculation and test load displacement curves

图15 极限状态钢梁应力云图. （a）正应力云图；（b）切应力云图Fig.15 Stress nephogram of a steel beam in the ultimate state: (a) nephogram of normal stress; (b) nephogram of shear stress

1800 mm的钢梁在1100 kN时达到极限状态，极限状态时应力云图如图16所示，提取加载全过程中对应的上翼缘检测线上应力分布如图17所示. 其等效应力云图中应力最大的区域和试验中屈曲损伤区域一致，说明用应力反映损伤情况是可靠的，建立了应力与磁信号的关系，也就实现了用磁信号来表征构件的损伤. 由图17应力分布曲线可知，该受力状态下应力分布曲线和磁信号分布曲线形态正好相反，但分布规律一一对应. 应力在右侧加载点附近出现最大值，正好和图11梯度曲线中破坏时磁梯度最大值点一致.

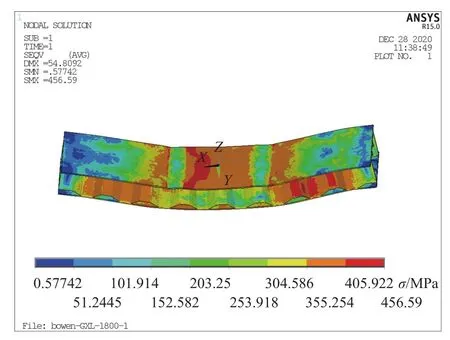
图16 试件极限状态等效应力云图Fig.16 Equivalent stress nephogram of specimen ultimate state

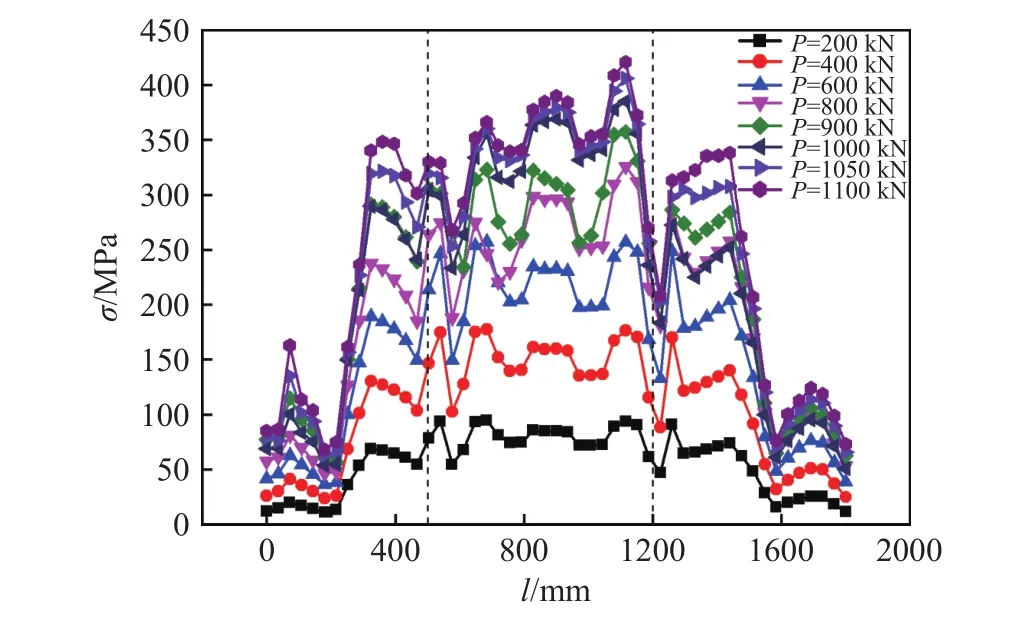
图17 有限元计算的1800 mm梁上翼缘应力分布Fig.17 Stress distribution on the upper flange of the 1800 mm beam calculated using the finite element method

2.2 损伤区域应力与磁信号关系

钢梁在4点受弯作用下，中间区域所受剪力为零，弯矩恒定，故称之为纯弯段. 钢梁损伤严重区域为纯弯段内，因此做出纯弯段不同检测力与磁信号关系曲线如图18所示. 在力的作用下，纯弯段各测点磁信号变化规律一致，在弹性阶段随着力的增大磁信号缓慢减小，达到屈服极限时，试件内部磁畴结构发生了改变，进入塑性阶段后立马向负值方向显著增大，此时试件已经向屈曲发展，到极限状态时磁信号开始分散发展. 则该力磁曲线可以清楚的判断出构件的屈服状态和极限状态.

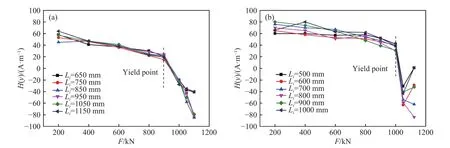
图18 钢梁纯弯段力磁分布曲线. （a）1800 mm 钢梁；（b）1500 mm 钢梁Fig.18 Magnetic distribution curve of force in the pure bending section of a steel beam: (a) 1800 mm steel beam; (b) 1500 mm steel beam

钢梁在中间纯弯段应力最大，且磁信号随加载等级的变化较均匀，因此选用有限元模拟的应力，作出纯弯段平均磁信号随平均应力变化的曲线如图19所示，并且对弹性阶段磁信号随应力的变化曲线进行了拟合，发现在本试验中弹性阶段磁信号随应力呈三次多项式的变化关系，两个钢梁的变化规律一致. 由应力与磁信号的关系，若测得磁信号数值即可大致得到应力变化情况，从而得知钢梁应力发展程度.

2.3 磁场梯度指数对钢梁损伤情况的表征

首先做出损伤区磁信号梯度峰值随荷载变化曲线如图20所示，为了更清楚进行磁场梯度对应力情况的表征分析，可将曲线整体变化过程分为4个阶段，Ⅰ为初始阶段，Ⅱ为临近屈服阶段，Ⅲ塑性阶段，Ⅳ破坏失稳阶段. 由曲线可得，第Ⅰ阶段随着加载等级的增大磁梯度值呈现三次函数的关系而增大；第Ⅱ阶段磁梯度值随应力的增大突然减小，此特点可作为判断试件进入屈服状态的重要依据；第Ⅲ阶段试件过屈服点进入塑性强化状态，此阶段磁梯度随应力的增加而稳定变化；第Ⅳ阶段时，试件临近破坏状态，此时磁梯度值随应力的增大又突然增大，此明显的变化可以作为判断试件出现损伤的临界值. 由此可见，磁场梯度与荷载关系曲线可将构件整个受力过程明显的区分为不同的受力状态，是用磁场变化表征应力状态的重要依据.

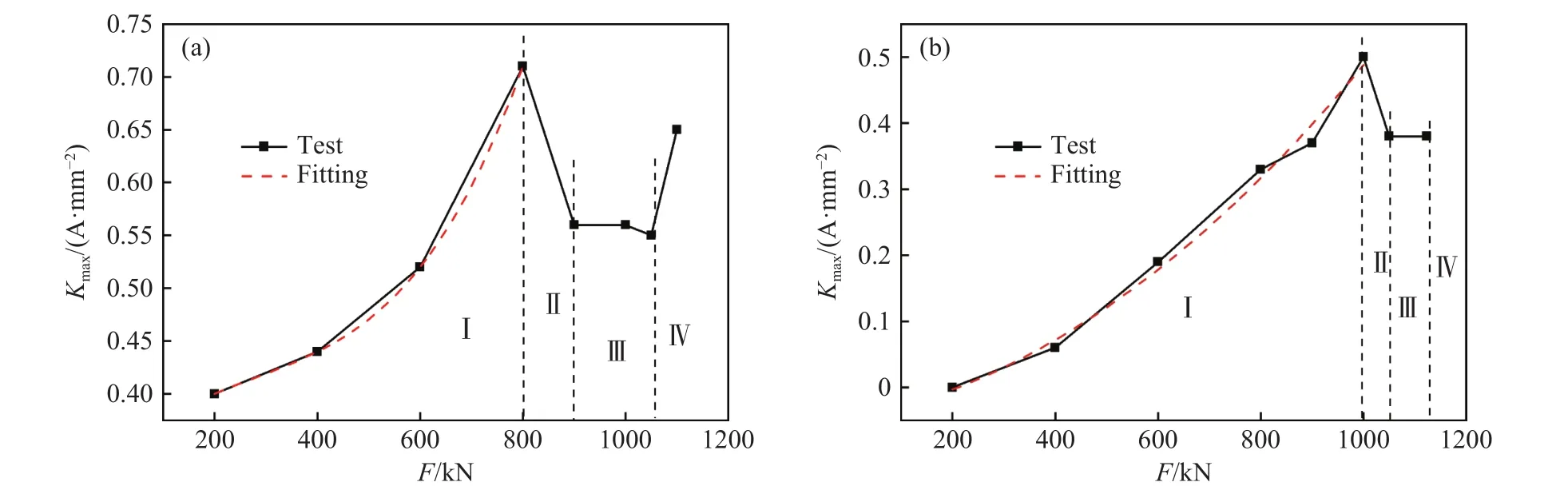
图20 钢梁翼缘力与磁信号梯度峰值曲线. （a）1800 mm 钢梁；（b）1500 mm 钢梁Fig.20 Peak gradient curves of the steel beam flange force and magnetic signal: (a) 1800 mm steel beam; (b) 1500 mm steel beam

做出磁场的梯度指数与力的关系曲线如图21所示，结果表明，梯度指数随加载等级的变化曲线在屈服点附近有明显的变化，弹性阶段呈现缓慢上升的趋势，在塑性阶段后突然下降，磁梯度指数可以准确表征试件的应力状态. 且由磁梯度指数与力的函数关系可以得到一个临界值，作为对检测构件濒临损伤，进入极限状态判断的参考.

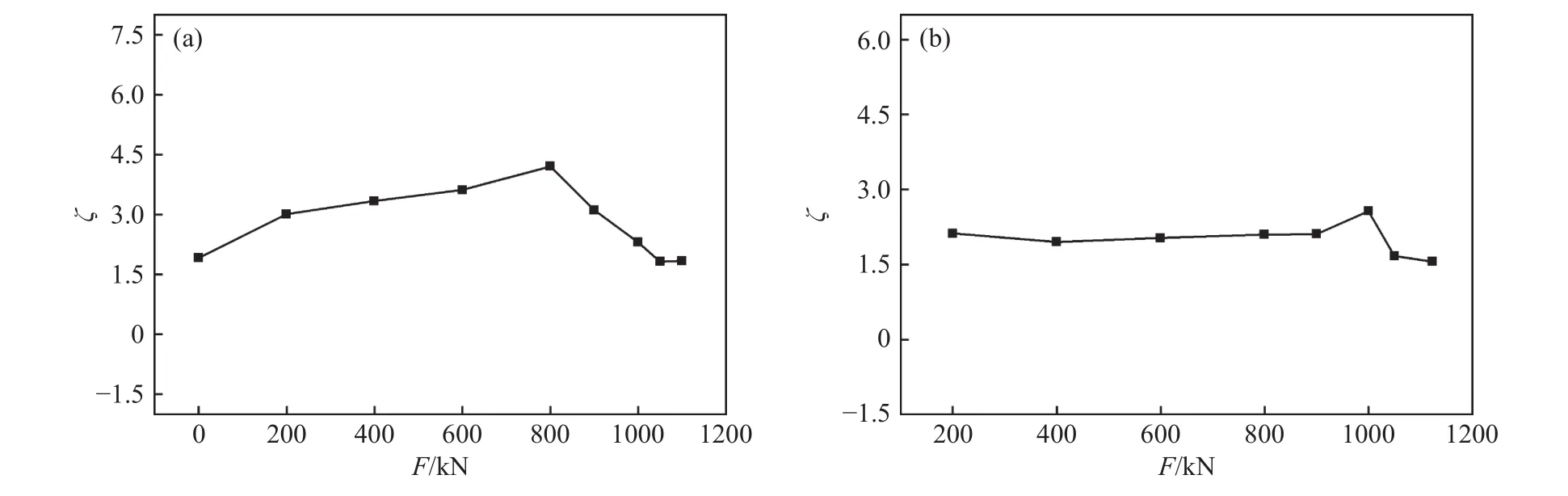
图21 力与磁场梯度指数关系曲线. （a）1800 mm 钢梁；（b）1500 mm 钢梁Fig.21 Exponential relationship curves between the force and magnetic field gradient: (a) 1800 mm steel beam; (b) 1500 mm steel beam

3 结论

（1） 钢箱梁上翼缘磁信号曲线与应力变化形态正好相反，磁信号曲线可以反映出钢梁应力集中区域，即发生屈曲损伤的区域. 磁信号曲线在进入屈服后发生反转，变为负值，且随应力变化的速度增快，由此可以判断构件进入塑性状态，即将发生损伤.

（2） 磁场梯度曲线在整个受力过程中都在加载点附近出现最大值，由此可以初步预测应力集中位置. 且随着荷载的增大，磁梯度最大值点不断向钢梁中间移动，破坏时完全处在中间段内，由此可以进行破坏状态的预警.

（3） 给出了钢梁翼缘损伤区域磁信号随应力变化的关系曲线. 并且发现磁场梯度与力关系曲线可将构件整个受力过程明显的区分为不同的受力状态，可以清晰的判断出构件初始、屈服、塑性、损伤4个状态.

（4） 提出了用磁场梯度指数来进行构件受力状态与损伤状态的表征，为金属磁记忆检测技术在桥钢箱梁方面定量评估和预警提供了依据和参考.

（5） 本研究对以后基于磁记忆的桥钢箱梁结构力磁关系研究提供了依据，以后的研究中还需要对论文中的结论进行大量试验验证，并对各种构件进行归类，找出各自的量化判别关系式.