基于麻雀算法的压缩感知观测矩阵优化方法

吕冠男，刘海鹏，卢建宏

（昆明理工大学 信息工程与自动化学院，云南 昆明 650000）

0 引言

奈奎斯特采样定理定义：当采样频率大于原始信号频率的两倍，就能从离散数字信号中恢复出原始信号。若按采样定理来采样，会使得采样信息量过大，导致存储空间的浪费。直到2006 年，压缩感知理论（Compressed Sensing，CS）[1-3]问世，这个问题才得到较为有效的解决。

压缩感知理论表明，当一个信号具有稀疏性，就可以用一个与原信号不相关的测量矩阵，以远低于奈奎斯特采样率采集到的信号测量值进行压缩采样，再用重构算法恢复出原始信号。压缩感知具有所需采样点少、数据储存量低等特点，在信号采集[4]、雷达探测、数据通信[5]等领域被广泛研究。

观测矩阵的特性决定了压缩感知理论是否可行，也决定了是否能够实现对信号的高概率重构，是压缩感知理论十分重要的一个部分。观测矩阵主要分为确定性矩阵和随机矩阵两大类。确定性矩阵包括循环矩阵、托普利茨矩阵等，随机矩阵包括高斯矩阵[6-7]、伯努利矩阵等。目前，大部分观测矩阵还存在一些不足，如托普利兹观测矩阵的重构性能较差等。观测矩阵需要满足有限等距准则[8]（Restricted Isometry Property，RIP），该准则表明，感知矩阵的性能与观测矩阵和稀疏矩阵之间的互相关性成反比，即矩阵间的互相关性越小，那么这个感知矩阵的性能就越好。

相比于确定性测量矩阵，随机测量矩阵具有所需测量数少、重建性能好的优点。但是随机测量矩阵由于计算的复杂性，使得储存量比确定性测量矩阵大，且矩阵重建的不确定性更高。因此，本文针对随机测量矩阵的缺点，提出将智能算法融入随机测量矩阵优化算法中，以此解决最优相关性的问题。

1 算法描述

1.1 麻雀搜索算法

由前文可知，随机矩阵优化算法并不能很好地解决最优相关性的问题，而麻雀搜索算法[9]（Sparrow Search Algorithm，SSA）具有较好的全局寻优特性。将SSA 应用到观测矩阵的优化中，可以使观测矩阵与稀疏矩阵的互相关系数降低，以此来提高信号的重构精度。

SSA 算法具有寻优能力强、收敛速度快等特点。以麻雀种群的觅食、警戒行为为基础建立麻雀算法数学模型的规则如下：

（1）发现者，负责搜索到具有丰富食物的区域，为所有的加入者提供觅食方向；

（2）加入者，跟随一个发现者，在觅食过程中，加入者跟随提供最好食物的发现者，在此发现者周围觅食；

（3）麻雀群体中的发现者和加入者是随时间变化的，但是比重不会发生改变；

（4）发现捕食者的麻雀会发出报警信号，当警报值过大，麻雀们会离开危险区域进入安全区域。

由此可见，SSA 中的麻雀可以分为发现者和加入者。发现者继续寻找食物，加入者跟随发现者觅食，且每一只麻雀随时都在对捕食者进行警戒。

尽管SSA 具有较好的全局寻优特性，但是SSA与其他基于种群的优化算法一样，都是随机地生成种群，这会使得在算法运行过程中，确定第一代发现者所耗的时间偏长。如果能改进算法，缩短第一批发现者的确定时间，就能在节约时间的同时减少算法迭代次数。另外，SSA 的位置更新方式会使算法陷入局部最优，使得全局搜索能力受损。而黄金正弦算法（Gold-SA）[10]通过随机生成每个维度的均匀分布来扫描搜索空间，相较于其他算法具有一定优势。将黄金正弦算法加入到SSA 中，能进一步加强SSA 的全局寻优能力，还能更快地确定第一代发现者，减少算法运行时间。

1.2 黄金正弦算法

于2017 年提出的黄金正弦算法与其他基于种群的算法一样，最初的种群也是随机生成的。但此算法的目的是生成每个维度均匀分布的初始种群，以此来达到更好的搜索效果。算法的表达式为：

式中：Vi表示第i个个体的初始值，ub是搜索空间的上限值，lb是搜索空间的下限值。

Gold-SA 算法引入了黄金分割系数x1和x2来更新位置，以此缩小搜索空间，使个体趋近最优值的速度更快。黄金分割系数如下：

传感器接收到一次指令后都会输出一串数据量很大的数据，如何快速接收并且不遗漏数据是一个需要解决的关键问题，针对数据量大的问题，选择在内存中开辟两块容量为300的临时缓存区，当有数据传来时，先进行存储，当存储完了之后再进行数据处理，这样便避免了数据丢失的问题.

式中：a和b为黄金分割比例初始搜索值，一般a=-π，b=π，。Gold-SA 算法通过下式进行位置更新：

此算法的基本流程是：先初始化参数，再设置黄金正弦相关参数；计算适应度值、计算黄金分割率，更新位置，计算适应度值，更新最佳位置并记录；判断迭代是否结束，结束得到最优位置则结束算法，不然重复前面的步骤。

1.3 改进麻雀算法

本文的算法将Gold-SA 算法应用在SSA 发现者和加入者的确定步骤中，使“搜索”和“开发”更加均衡，缩小了搜索空间的同时还能减小陷入局部最优的概率，获得更好的全局特性。加入改进麻雀算法优化观测矩阵的流程如图1 所示。

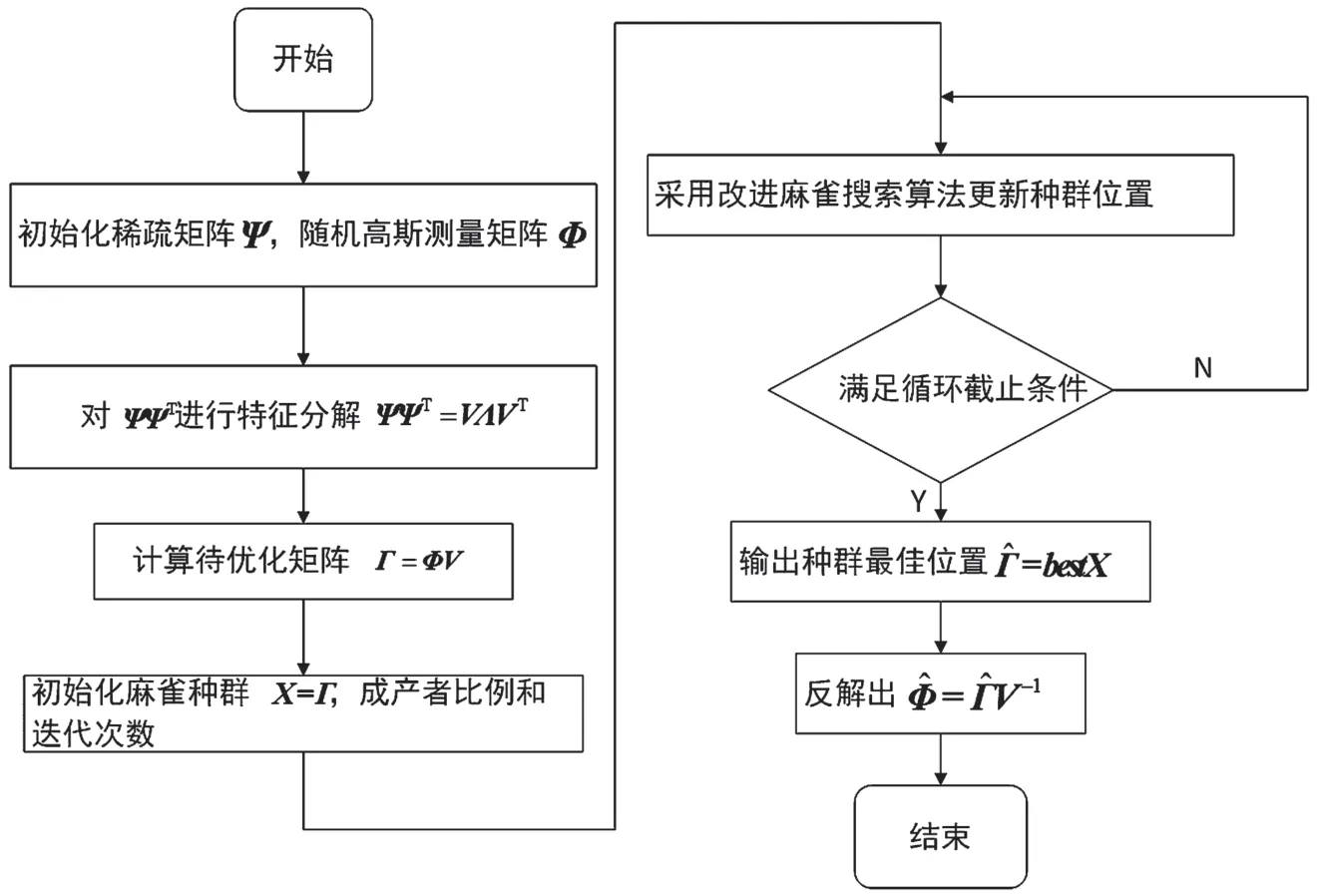
图1 优化观测矩阵流程图

如图1 所示，整个过程中，首先要初始化稀疏矩阵Ψ、随机高斯矩阵Φ，然后进行特征分解，再计算出待优化矩阵Γ，之后通过改进麻雀算法找到最佳位置，最后求出与最佳位置对应的最佳测量矩阵并输出。

2 实验部分

以下仿真结果均在Matlab R2017a 环境下得到。

2.1 算法收敛速度比对

算法收敛速度的快慢在很大程度上影响算法的运行时间，收敛速度越快，运行时间越短。因此，为了验证本文改进的麻雀算法比原始麻雀算法的运行速度更快，首先做了改进麻雀算法与传统麻雀算法的收敛速度对比实验。实验循环次数为50 次，结果如图2 所示。

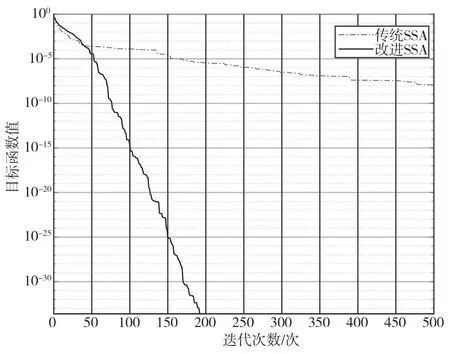
图2 收敛速度对比实验

在图2 中可以清晰地看到，相比于传统的SSA算法，本文提出的改进算法有更快的收敛速度。当迭代次数为190 次时，本算法基本完成了对目标函数的逼近，而传统的SSA 算法在500 次迭代完后依然离目标较远。由此可见，本文提出的改进SSA 算法相比于传统的SSA 算法而言，大大减少了迭代次数，缩短了算法运行时间。

2.2 图像重构实验对比

之前的实验只是简单地证明了本文提出的改进算法相比于传统的SSA 算法具有更快的收敛速度，在这一部分，给出通过两种算法分别构造出的测量矩阵结合OMP 算法、LAOMP 算法重构出的二维图像直观视觉效果对比图。采样率选择0.5，实验10 次取平均值，结果如图3 所示。

图3 高斯随机矩阵

图4 麻雀算法矩阵

图3～图5 中，子图（a）、（b）、（c）分别代表原始图片、OMP 算法重构出来的图片和LAOMP 算法重构出的图片。仅从图片上看，区别不是很明显，但本文的改进算法还是比传统的麻雀算法求解的矩阵和高斯随机矩阵重构出的图片要清晰一点。为了使实验更具有说服力，下面对实验的各项数据进行对比，实验数据如表1、表2 所示，以重构图像的峰值信噪比（Peak Signal to Noise Ratio，PSNR）、平均互相关系数（UAV）、运行时间（TIME）、相对误差（Relative Error，RE）作为算法优劣的评判标准，定义如下。

图5 改进麻雀算法矩阵

（1）PSNR 主要用来衡量图像重构质量的性能，定义为：

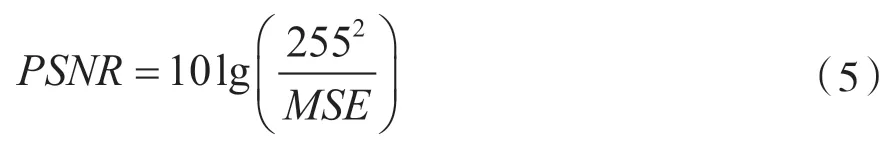
（2）RE 为相对误差，定义为：

（3）UAV 为平均互相关系数，即绝对值大于或等于Gram 矩阵非对角元素的平均值，用以评价矩阵的整体相关性，定义为：

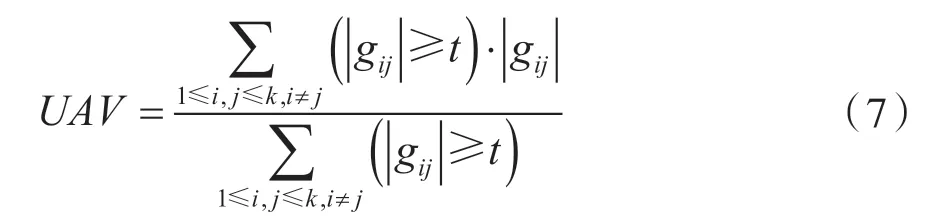
当t=0 时，可获得一个绝对项的简单平均值，gij表示Gram 矩阵的第i行j列的值。Gram 矩阵可表示为：

性能指标对比如表1、表2 所示。

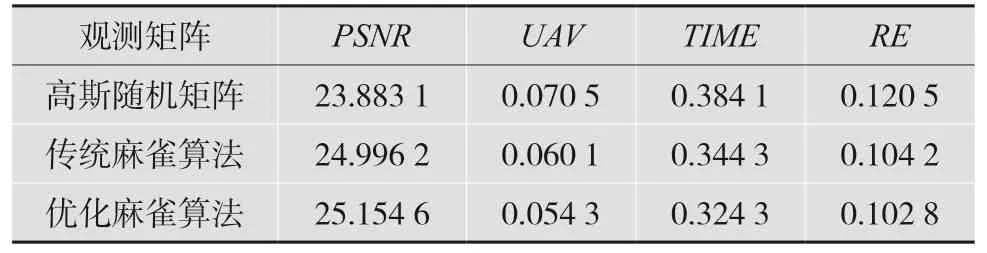
表1 OMP 算法重构图像数据对比

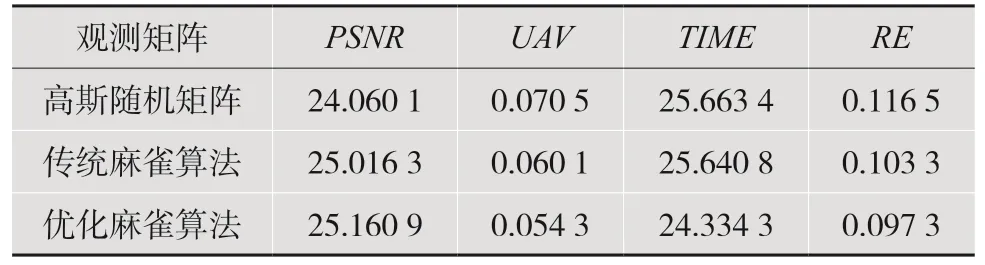
表2 LAOMP 算法重构图像数据对比

由表1、表2 可知，采样率为0.5 时，无论是采用OMP 算法还是LAOMP 算法，本文算法构造的矩阵比传统麻雀算法和高斯随机矩阵重构出来的图像的峰值信噪比更高，运行的时间更短，重构误差也最小。本文算法构造的观测矩阵与稀疏矩阵的互相关系数为0.054 3，而高斯随机矩阵与稀疏矩阵的互相关系数为0.070 5，传统麻雀算法为0.060 1，同样表明用本算法构造的感知矩阵的性能要比其他两种算法好。

3 结语

本文就利用随机矩阵构造观测矩阵并不能解决最优相关性问题进行改进，引入麻雀搜索算法加强全局寻优性，使得观测矩阵与稀疏矩阵的互相关系数降低，以此提高信号的重构精度。再将黄金正弦算法应用在SSA 发现者和加入者的确定步骤中，使“搜索”和“开发”更加均衡，降低了由于SSA 随机生成种群而造成的寻优时间过长造成的影响，减少了算法迭代次数的同时，也使算法保持原有的寻优能力。经过二维图像重构仿真对比和算法收敛速度实验对比，发现该算法相比于随机矩阵和传统SSA 具有更快的运行速度和信号恢复能力。下一步的工作计划是寻找新的智能种群算法与SSA 结合，以求进一步降低互相关系数。