基于遗传算法的二次供水低位水箱调度方案优化

高雨妃，周立典，张 雪，夏星宇，赵平伟，信昆仑

(1.同济大学环境科学与工程学院，上海 200092；2.苏州市水务集团有限公司，江苏苏州 215000；3.上海城投水务<集团>有限公司，上海 200431)

近年来，高层建筑越来越多，市政管网供水压力往往无法满足高层用户的用水需求[1]，因此，二次供水系统的应用愈加普遍。其中，低位水箱的应用极为广泛，其主要有3个作用[2]：(1)二次加压是其最根本的作用，水箱对自来水进行二次加压后供给高层建筑用户，使市政管网不必一直维持很高的压力；(2)提高供水安全性，当水厂和管网施工、维修，导致局部区域停水时，水箱的储水可以在一段时间内继续供水，减小对用户的影响；(3)调蓄节能，在用水低峰时蓄水，用水高峰时供水，缓解供需矛盾，调节系统水量，节能效果显著。

近些年，为了更好地利用水箱的功能，国内外研究人员对水箱的调控方式进行了研究。祁司亮等[2]应用穷举法使用3种不同的模式(“即用即进”“均匀进水”和“削峰填谷”)对虚拟管网的水箱进行调节，最终得出结论：“削峰填谷”的调控方式可以使管网压力波动强度最小，即用即进的方式压力波动强度最大，均匀进水的方式调控效果介于这2种调控方式之间。为了解决大规模管网水箱调控优化问题，同年，祁司亮等[3]使用遗传算法对一个虚拟的小型管网的水箱调控组合进行优化，结果表明：对所有的水箱采用“削峰填谷”式调控时，可最大幅度地降低管网压力波动、提高最不利点压力，但并未对水箱起到的节能降耗作用进行讨论。2019年，赵丹等[4]根据液位信息和用水高峰期信息实现阀门自动开闭，从而改变现有水箱“随用随进”的进水模式，充分发挥二次供水设施的调蓄功能。同年，Khatavkar等[5]使用遗传算法对一个三水箱的管网实现水箱和水泵的联合运行优化，以水泵的电耗费用和水箱的周转率作为目标函数，使用遗传算法降低水泵的能耗，但并未对水箱对于管网的“削峰填谷”效应做出评估。

总体上，目前文献中对于水箱的“削峰填谷”效应以及其所起到的节能降耗作用并没有进行综合的讨论分析，且对于具有大量二次供水低位水箱的管网未做讨论。

本研究分别针对小型管网算例和SZ市某水厂服务范围的具有大量二次供水低位水箱的实际管网，以“削峰填谷”效应最大化为目标，建立二次供水低位水箱优化问题的数学模型，采用遗传算法寻找二次供水低位水箱优化运行的最佳方案，并进一步对其节能降耗效果进行评估。

1 供水管网二次供水优化模型

1.1 控制变量

对于低位水箱二次供水模式，一般采用水位控制器来实现对水箱的进水控制。进水阀门在高水位时关闭，在高水位和低水位之间时保持关闭，在低水位时开启。

以各水箱各个时刻在24 h下进水管阀门状态Si,t(i为时间点，t为水箱编号)作为控制变量。

1.2 目标函数

理论上，对于单台水泵，流量越大扬程越低，为保证输出水压相同，需水量增大时需要开启更多的水泵。通过二次供水水箱的调蓄作用，可以对二级泵站的出水流量进行“削峰填谷”，充分利用用电低谷时的电价优势，同时减小整个管网的压力波动。因此，可以将二级泵站出水流量的波动强度Qv作为二次供水水箱实现“削峰填谷”效能的度量值。本研究将最小化Qv作为目标函数，计算如式(1)。

(1)

其中：Qv——二级泵站出水流量的波动强度，m3/h；

Qi——第i时刻的出厂流量，m3/h；

1.3 约束条件

1.3.1 水箱水位约束

最高、最低水位约束范围如式(2)。

Htmin≤Ht≤Htmax(t=1，2，…，N)

(2)

其中：Htmin、Htmax——水位约束上下限，m；

N——二次供水水箱总个数。

考虑到供水管网每日运行的周期性特征，24 h周期水箱水位表达式如式(3)。为保证水箱0时水位与24时水位相同，在目标函数中加入罚函数，如式(4)。

Ht0=Ht24

(3)

(4)

其中：Ht0、Ht24——水箱0时刻、24时刻水位，m；

sumΔH——所有水箱24 h水位差之和，m。

水位约束通过罚函数形式转化到目标函数中，水箱0时与24时的差值乘以系数得到罚函数。

1.3.2 管网的水力平衡约束

管网的水力平衡约束计算如式(5)～式(6)。式(5)中对流入和流出节点j的管段流量求和，流入节点的流量定为负值，流出节点流量则定为取正值。

∑k∈sj(±qk+Qj)=0

(5)

(6)

其中：j——节点数；

k——管段总数；

Sj——节点j的关联集；

qk——管段流量，L/s；

Qj——节点j流量，L/s；

HFk——管段上游节点水压高程，m;

HTk——管段下游节点水压高程，m;

hk——管段水头损失，m；

Sfk——管段摩阻系数；

n——常用1.852～2，本文取2；

hpk——水泵扬程，未设置泵站时hpk取0，m。

1.3.3 供、用水量平衡约束

供、用水量平衡约束如式(7)。

∑Qj=∑Dj

(7)

其中：Dj——节点j的用水量，m3/h。

1.3.4 监测点水压约束

监测点水压约束如式(8)。

Hrmin≤Hr≤Hrmax(r=1，2，…，Ns)

(8)

其中：Hrmin、Hrmax——监测点水压约束上下限，m；

Ns——水压的监测总点数。

2 模型求解

2.1 遗传算法参数设置

上述最优化模型是既有离散变量(水箱阀门启闭)又有连续变量(出厂水流量)，且包含不等式约束的单目标优化问题，适合采用遗传算法进行求解[6]。

(1)编码方式

采用二进制进行编码，其中，0表示阀门关闭，1表示阀门开启。采用分时段控制水箱进水管阀门的开闭，同时考虑实际应用时的操作可行性，避免水箱进水频繁启闭。根据自来水公司调度技术人员建议，设定每4 h进行一次状态变更，因此，每个编码表示4 h内的阀门开闭状态，每个水箱阀门24 h的控制方案由6个二进制数字组成，每个个体表示所有水箱阀门1 d内的控制方案，是一串长度为6倍水箱总数的二进制数组。例如：101100，表示0:00—4:00，阀门开启；4:00—8:00，阀门关闭；8:00—16:00，阀门开启，16:00—24:00，阀门关闭。

(2)适应度函数

目标函数Qv越大的染色体代表出厂水流量波动性越高，适应度越低，在进化中被淘汰的概率越大，因此，设计个体适应度计算如式(9)。

F=Qv+φ×sumΔH

(9)

其中：φ——罚函数sumΔH的惩罚系数，本研究中φ取1 000；

F——个体适应度。

F表明当前解对应二次供水水箱控制方案的优劣，F越小，表明该方案的二级泵站出水流量的波动强度越小，该个体在进化过程中被保留的概率越大；F越大，表明该方案的二级泵站出水流量的波动强度越大，该个体在进化过程中被保留的概率越小。

(3)遗传算子

遗传算子的设置如下[7]。①选择：采用精英策略，每代保留适应度最高的2个个体。②交叉：采用单点交叉，交叉概率为0.80。③变异：采用基本位变异法，在随机指定的若干位置上，对个体的基因以一定概率进行变异，本研究中采用的变异概率为0.01。④终止规则：采用最大遗传代数法，当遗传进行到最大代数50，或者最优解连续若干代后保持不变时，算法终止。

2.2 算例研究

2.2.1 算例管网

算例管网包含1个水源、4个水箱(编号为6、17、18、19)、4个流量控制阀(TCV)(编号为8、17、18、19)以及13个用水节点。做出如下假设：出厂水(水库节点7)水压恒定、用水节点的用水量随时间变化、所有用户24 h用水规律相同、均为普通居民生活用水、有早晚2个高峰。优化过程与模拟结果如下。

①水箱水位限制

使用EPANET软件的Simple Control Editor，根据水箱水位对进出水进行控制，控制语句格式如下。

LINK 8 CLOSED IF NODE 17 ABOVE 2.300

②优化过程

针对算例管网，先将阀门控制方案对应的二进制编码转化为分时段控制语句，如，对于算例中的阀门8，若其控制方案的二进制编码为100010，则通过Python写入EPANET软件的Simple Control Editor的语句格式如下。

Valve 8 OPEN AT CLOCKTIME 0

…

Valve 8 OPEN AT CLOCKTIME 3

Valve 8 CLOSED AT CLOCKTIME 4

…

Valve 8 CLOSED AT CLOCKTIME 8

…

将1 d的控制方案(表1)全部写入运行管网模型后，计算该调控方案的目标函数值，最大遗传代数设置为50，同时连续10代最优个体不变也终止，其余参数设置同2.1小节，延时模拟时间设为24 h，即1 d为一组水箱运行调控的周期。

表1 进水管阀门控制方案

③模拟结果

优化前：仅根据水位对4个水箱进行调控，根据水位来控制进水阀门的开闭，超过设定的最高水位时关闭阀门，低于设定最低水位时开启阀门，在最高水位到最低水位的范围内阀门均关闭。

优化后：在对水箱进水管阀门进行水位控制的基础上，增加分时段控制。利用EPANET软件延时模拟确定各调蓄水箱24 h各时刻的进水管阀门状态。当水箱水位不满足设定值时，以水位调控优先。

出厂水流量和压力优化前后对比如图1～图2所示。对水箱的调控方式进行优化后，出厂水流量和压力的波动明显减小，说明水箱对管网流量与压力的“削峰填谷”效应增强；在2个用水高峰期，出厂水流量明显下降，说明水箱的调蓄作用降低高峰期水厂的供水负荷，提高用水点的压力；在用水低峰期，出厂水流量和压力也保持稳定。

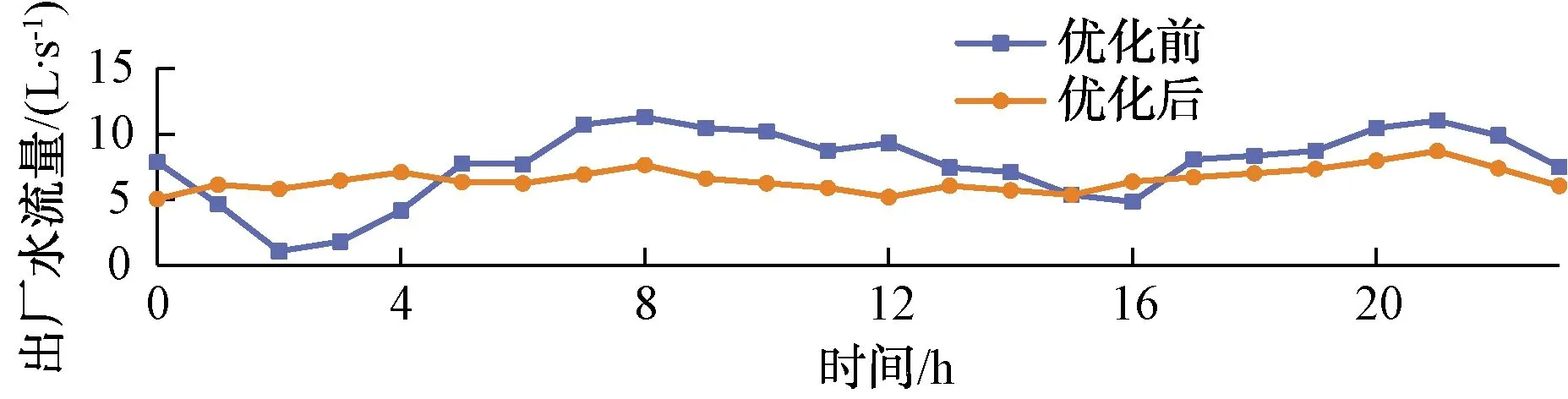
图1 优化前后出厂水流量变化

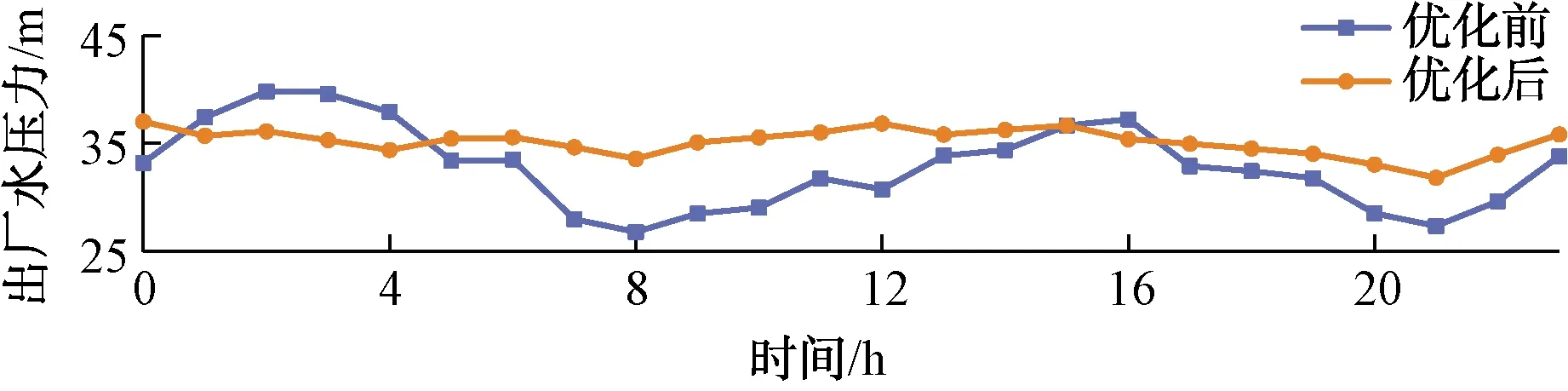
图2 优化前后出厂水压力变化

针对水箱的调蓄方案对管网供水能耗的影响，还需分别从二级泵站的能耗、二级泵站出水流量的波动强度对水箱调蓄优化方案进行评估。

二级泵房供水一日所需能耗理论值计算如式(10)。

(10)

其中：ρ——水的比重，ρ取1 000，kg/m3；

g——重力加速度，g取9.81，m/s2；

Qps,i——第ih二级泵房出水流量，m3/h；

Hps,i——第ih二级泵房出水压力，m；

E——二级泵房供水一日所需能耗理论值，kW·h。

由式(10)计算得出，优化后水厂二级泵站理论能耗值可降低5.76%，具有较明显的节能降耗效果。

2.2.2 SZ市管网应用

算例管网如图3所示，并将优化方法应用于SZ市某水厂供水范围内的管网(图4)。

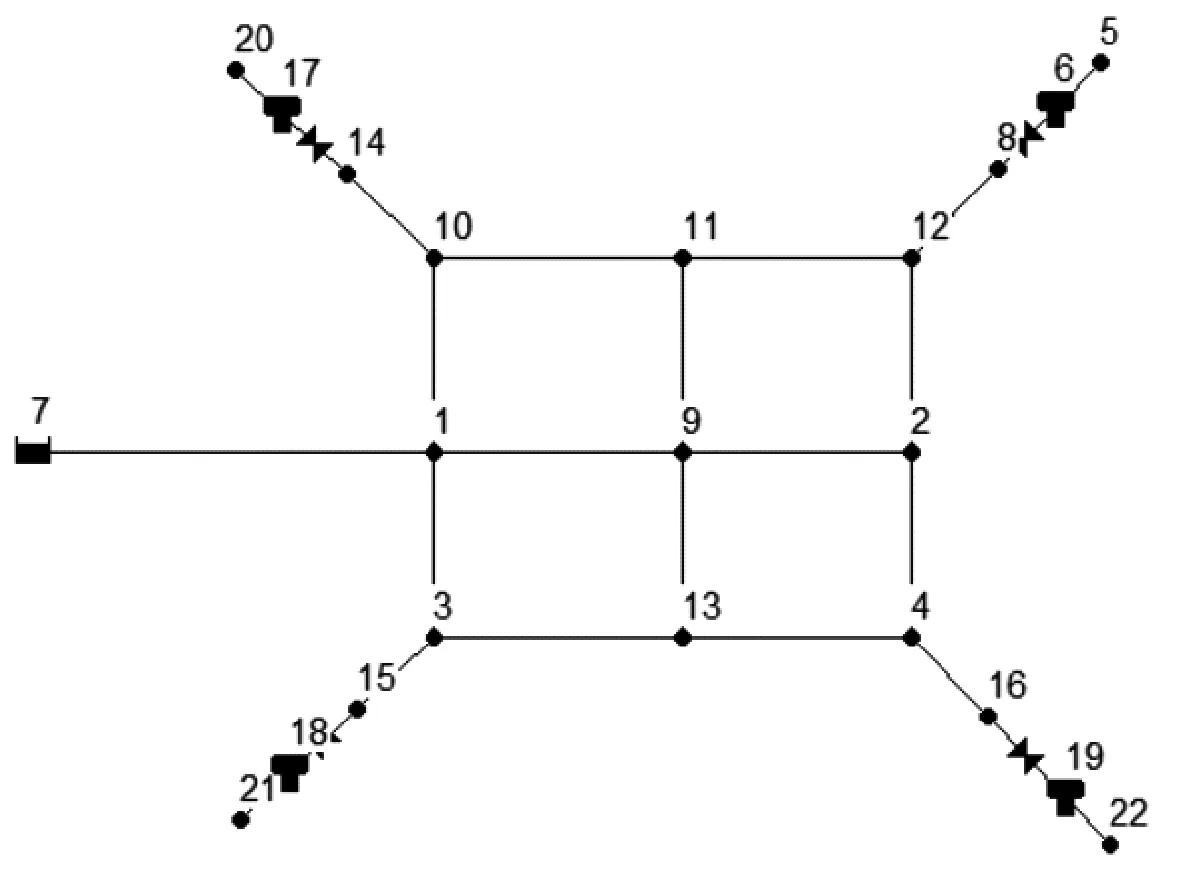
注：图中数字为节点编号

图4 SZ市管网拓扑

优化SZ市88个二次供水水箱运行状态，并根据运行结果可知，出厂水压力从1 133.84 m降至1 031.92 m，降低了8.99%；优化后管网理论能耗值可降低6.83%。优化前后出厂水流量和压力变化如图5～图6所示。通过低位水箱的进水控制调度，可实现对出厂水流量的“削峰填谷”作用，同时水厂二级泵站调度可通过不同型号水泵组合、变频控制等方式进行出厂供水压力调节，当出厂水流量减少，相应管网水头损失降低，对出厂压力的需求也相应减少。因此，高峰时的出厂压力也通过泵站调度随之降低，从而进一步实现节能降耗的效果。

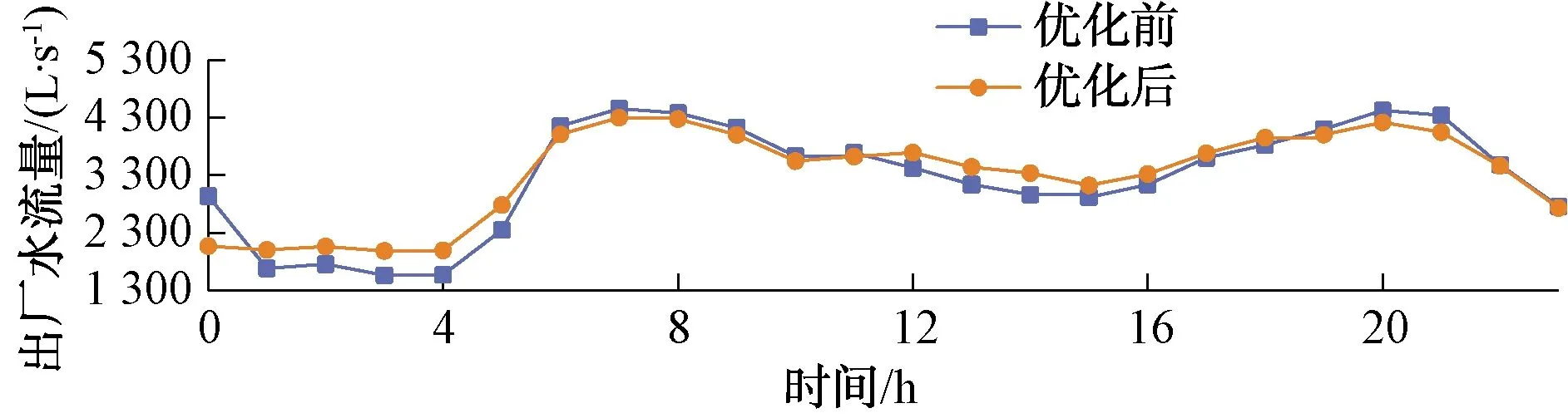
图5 优化前后SZ市出厂水流量变化

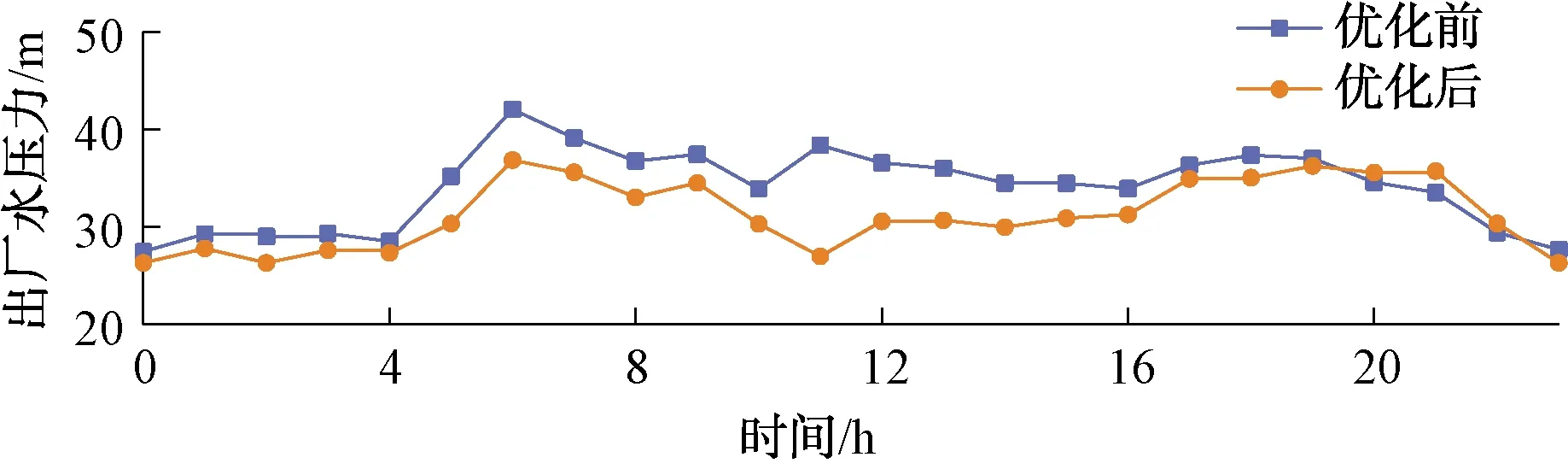
图6 优化前后SZ市出厂水压力变化

3 结论与建议

本文使用带有精英策略的遗传算法优化二次供水水箱调度方案，介绍模型建立和求解过程，在水位控制的基础上，增加分时段控制，将优化后的调度方案应用到算例管网和SZ市管网中。水箱的“削峰填谷”作用得到充分利用，使得出厂水的流量波动降低，降低用水高峰期的供水负荷，出厂水压力更加平稳，实现了二级泵站节能降耗。

由于我国供水行业二次供水设施改造在不断深入推进，我国城市供水系统中二次供水低位水箱也在逐渐增加，本文所提出的二次供水低位水箱调度有助于供水企业通过协同二级泵站和二次供水设施的运行调度，实现供水水压水量的稳定和节能降耗运行。值得注意的是，本研究在优化过程中，SZ市的水箱的数目过多，导致水箱的水位约束成为强约束，使得水箱的水位在24 h后回归初始值这一条件较难满足，需要在优化的结果中综合比较，筛选出最符合水箱约束条件的结果。因此，下一步的研究可以针对水箱的水位约束条件做进一步的优化，以保证方案的合理性以及加速算法的收敛。