基于ReliefF的层次分类在线流特征选择算法

张小清，王晨曦*，吕彦，林耀进

（1.闽南师范大学计算机学院，福建漳州 363000；2.数据科学与智能应用福建省高校重点实验室，福建漳州 363000）

0 引言

在人工智能蓬勃发展的时代，数据信息的产生速度呈指数式急剧上升，分类任务面临着规模越来越大，如样本数目多、特征维度高、类别数量大的挑战。与此同时，数据的类标记空间往往存在层次化结构。如图1 所示，胃肿瘤（gastric tumors）是消化系统常见疾病，可分为恶性和良性。恶性肿瘤包括胃癌、恶性淋巴瘤和恶性间质瘤等。良性肿瘤可分两大类：一类来源于黏膜的良性上皮细胞瘤，如胃腺瘤、腺瘤性息肉等；另一类是良性间叶组织肿瘤，如间质瘤、脂肪瘤和神经纤维瘤等。显然，胃肿瘤的组织关系存在层次结构化。间质瘤是1983 年被首次提出，以DOG1、CDll7、CD34 阳性为主，c-kit 或PDGFRA 基因功能获得性突变是重要的分子特征，未定义之前易与其他常见的良性间叶组织肿瘤相混淆。由此可见，研究层次化结构分类学习具有重要意义。

图1 胃肿瘤层次结构Fig.1 Hierarchical structure of gastric tumor

在层次化分类学习建模过程中，该类数据的特征空间表现出超高维和演化性［1］的特点。为减少特征高维度带来的计算和存储开销，特征选择能够对数据特征进行筛选，有效地降低数据特征空间的高维性，降低样本被误分的概率。Relief 算法是一种高效的过滤式特征选择方法，1992 年由Kira 等［2］提出并用于解决单标记问题。为能够处理多标记问题，2013 年Spolaôr 等［3］在Relief 算法的基础上进行改进得到ReliefF 算法。学者们结合标记相关性对ReliefF 算法进行扩展。Kong 等［4］提出MReliefF 算法，然而，这些特征选择算法忽略了类别空间层次结构关系。目前，已有许多面对层次化结构数据的特征选择算法被提出：Grauman 等［5］提出了一种新的视觉识别度量学习方法，集成了关于对象层次结构的外部语义；Hwang 等［6］提出了一种语义核林方法，使用多个层次分类来表示对象类别的不同语义视图；Zhao 等［7］提出了一种新的具有递归正则化的分层分类特征选择框架，同时考虑类别之间的父子、兄弟关系。

这些已有的分层特征选择算法假设特征空间是静态的、先前已知的，未考虑建模任务中特征的动态性和不确定性，因此把动态的、未知条件下的特征选择问题转换成流特征概念下的在线特征选择问题的研究十分重要。针对传统的二分类学习问题，Wu 等［8］提出了一种在线流特征选择框架；陈祥焰等［9］提出了基于邻域粗糙集的高维类不平衡数据的在线流特征选择算法，用于选择在大类和小类之间具有高可分离性的特征。针对多分类学习问题［10］，Lin 等［11］提出了基于模糊互信息的多标记在线流特征选择算法；Liu 等［12］提出了基于邻域粗糙集的多标记在线流特征选择算法。

这些已有的层次特征选择算法未考虑在线流特征的表现形式，而传统的在线流特征选择算法能够实现动态特征的在线处理，但忽略了类别之间的层次关系。为此，本文基于ReliefF 算法［3］提出层次分类学习在线流特征选择算法OH_ReliefF（Online Hierarchical streaming feature selection based on ReliefF algorithm）：利用标记之间的层次关系对ReliefF 算法进行改进，使ReliefF 算法能够处理层次化结构数据，将新的特征权值计算方法与在线重要性分析和在线冗余性分析策略相结合，设计相关算法来构建层次分类学习的在线流特征选择框架。本文的主要工作如下：

1）在ReliefF 算法的基础上，将排斥策略与兄弟策略结合作为划分标记异类的标准，定义一种能够处理分层数据的特征权重计算方法HF_ReliefF（Hierarchical Feature weights calculated based on ReliefF algorithm）。

2）提出OH_ReliefF，将特征的层次关系与流特征选择框架相结合，为层次数据集在线选择一个较优的特征子集。

3）与传统的在线特征选择算法相比，本文算法在6 个数据集上的平均预测精度值与次优算法相比提高了10%，在LCA-F1（Lowest Common Ancestor-F1）分层指标上相较于次优算法提高了5%，并且TIE（Tree Induced Error）值降低了25%，说明本文算法可以很好地应对分层流特征选择问题。

1 相关基础

1.1 类别的层次结构

在层次分类学习中，一般把类别的层次结构分成树结构和有向无环图结构两种［13］，本文只考虑类别的树结构关系。树结构的“从属”可以用序对(D，≺)来表示，具有不可逆性、反自反性和传递性［14］等特性，其中D表示样本的标记空间，≺表示从属关系。对于∀di，dj，dk∈D，树结构的从属关系的特性描述如下：

1）不可逆性：若di≺dj，则dj⊀di。

2）反自反性：di≺di。

3）传递性：若di≺dk且dk≺dj，则di≺dj。

利用树结构中的从属关系来表达层次结构中节点之间的父子关系和兄弟关系，描述如下：

1）父子关系：若di≺dj，则称节点dj是节点di的父节点；

2）兄弟关系：若di≺dk且dj≺dk，则称节点dj是节点di的兄弟节点，并且节点dk是点节点di、dj的父节点。

1.2 ReliefF算法

定义1［3］设U表示样本的集合，对∀xi，xj，xk∈U，Δf(xi，xj)表示样本xi和xj在特征f(f⊆F)下的欧氏距离，并且Δ 函数满足以下定义：

1）Δf(xi，xj)≥0，当且仅当xi=xj时，Δf(xi，xj)=0。

2）Δf(xi，xj)=Δf(xj，xi)。

3）Δf(xi，xj)≤Δf(xi，xk)+Δf(xk，xj)。

定义2［3］对∀xi∈U，决策属性D在特征f⊆F将U划分为样本xi的同类近邻样本集合Hi和异类近邻样本集合Mi。具体表示如下所示：

其中Label(xi)表示样本xi的类别。

定义3［3］∀xi∈U(i≥1)，在样本xi下，特征f⊆F衡量对决策属性D的划分能力用权重Wi来表示。权重Wi计算公式如下所示：

其中：分别取前k个样本作为样本xi的最近同类近邻和最近异类近邻；表示样本xi的第j个同类近邻样本，表示xi的第j个异类近邻样本；C表示样本xi类别的异类。

2 基于ReliefF的层次分类在线流特征选择

本章将排斥策略与兄弟策略相结合应用到ReliefF 算法中，并将改进的ReliefF 算法拓展到层次分类学习的在线流特征选择问题，基于ReliefF 算法提出层次分类学习模型的两种在线特征评估准则。

2.1 层次类别的划分策略

传统的ReliefF 特征选择算法在划分样本同类、异类时往往没有将类别之间的关系考虑进去，通常采用排斥策略［15］来划分类别。排斥策略描述如下：如果样本的类别为di(di∈D)，则所有不同于di的类别都作为异类。针对的ReliefF 算法存在的不足，若样本的类别具有层次结构，利用树结构的层次关系可以更好地衡量类别之间的划分：利用父子关系来划分同类和异类称为包含策略，即若样本的类别为di，则di与该节点所有的孩子节点均视为同类，除此之外的类别均为异类节点。利用节点之间的兄弟关系来划分同类异类的策略称为兄弟策略，兄弟策略认为节点di的同类为自身，节点di所有兄弟节点称为异类。

2.2 面向层次化数据的ReliefF算法

定义4矩阵S∈Rl×l用于描述节点之间的兄弟关系，l表示层次树中叶子节点个数。Si表示与节点di有兄弟关系的集合，Sij的值用来区分节点di和节点dj是否存在兄弟关系。兄弟矩阵S用形式化描述如下：

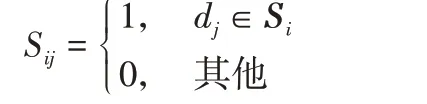
对于1≤j≤l，若∃Sij=1，表示节点dj是节点di的兄弟节点，节点di的异类为dj。此时，节点di也是节点dj的兄弟，可以看出兄弟矩阵S是一个对称矩阵。

定义5∀di∈D，特征f⊆F衡量对类别di的划分能力用权重Wdi来表示。权重Wdi如下所示：

其中：sim表示所有类别为di的样本；若∃Sij=1，类别di的兄弟节点为dj，dif表示所有类别为dj的样本；否则采用排斥策略来划分样本，dif表示所有不同于类别为di的样本。

面向层次化数据的特征权重计算算法HF_ReliefF 描述如算法1 所示：

算法1 HF_ReliefF。

输入 特征矩阵data∈Rn×p，类别矩阵D∈R1×l，层次树结构tree，近邻个数k；

输出 预测特征权值向量W。

区别于传统的ReliefF 算法，HF_ReliefF 算法考虑类别之间的层次关系，并且以每个类别作为单位来计算特征的权重，利用特征对近邻样本的划分能力来评价特征的重要性。

2.3 OH_ReliefF算法

为解决层次分类学习中特征空间的动态性和未知性问题，选择出对决策属性具有高分离性并且低冗余性的特征，本节基于HF_ReliefF 算法介绍两种在线评估准则。

2.3.1 在线特征重要性分析

若同类样本之间的距离越小，异类近邻样本之间的距离越大，则特征权值计算结果越大，表明所选特征对决策属性划分的能力越大。重要的特征应该使得同类样本的距离更加接近，而异类样本之间的距离更远。

因此，如果新特征的加入可以提高候选子集的权重，即W{ft}∪st-1>Wst-1，说明ft对候选子集是有意义的非冗余特征，能够提高候选子集对决策属的划分能力；否则认为候选子集St-1存在特征与ft相互冗余。

2.3.2 在线冗余分析

若新特征的加入不能提高候选子集的权重，即W{ft}∪st-1≤Wst-1，则对ft调用冗余分析。记S′=S∪{ft}，对集合S′中所有的特征利用式（3）分别计算与该集合中其他特征之间的协方差。

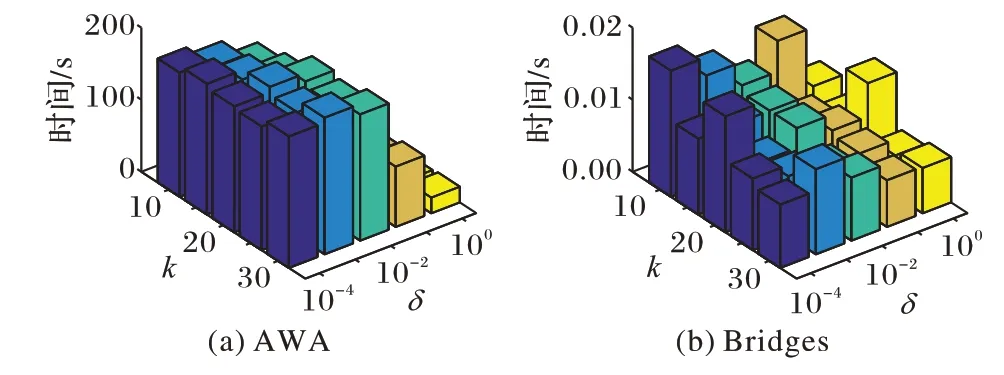
若特征fi与特征fj的协方差为Cov(fi，fj)=0，说明特征fi与特征fj相互独立，特征之间不存在冗余关系；否则，则认为新特征ft的加入，使得特征集合S′中的特征fi与特征fj冗余，比较特征fi与fj之间的权重大小，若Wfi

根据式（2）与式（3），提出基于ReliefF 算法的层次分类在线流特征选择算法OH_ReliefF，描述如算法2 所示。

算法2 OH_ReliefF 算法。

输入特征矩阵data∈Rn×p，层次树结构tree，近邻个数k；

输出 特征序列S。

算法2 主要包含两个阶段：在线特征的选择阶段以及特征的冗余分析阶段。在t时刻，新特征ft到达，执行算法的第2）步计算特征的权重Wt。当Wt<δ时，直接删除特征ft；否则执行第4）步，计算特征集合权重WS′，其中S′=S∪{ft}。当WS′>WSt-1时，则执行第6）步将特征加入特征子集中；否则需执行第7）～16）步。在线冗余分析阶段，对S′中每个特征执行第9）～15）步。在第9）步中随机选择两个特征fi、fj并计算特征之间的协方差，当Cov(fi，fj)≠0 时，则可删除冗余的特征。

假设 |U|表示论域U的样本个数，|F|表示条件属性F的属性个数，|l|是层次结构中的叶子节点个数，当前所选特征子集数量为|St|，则计算权重Wt的时间复杂度为；在在线特征重要性分析阶段，遍历所有类别所需时间复杂度是；当执行在线冗余更新阶段，算法最差时间复杂度为。

3 实验与结果分析

3.1 实验数据集

本文使用6 个数据集来测试OH_ReliefF 算法的性能，其中包括2 个蛋白质数据集和4 个图像数据集，具体情况如表1 所示。

表1 数据集描述Tab.1 Description of datasets

3.2 评价指标

在本文的实验中，基于K 最邻近（K-Nearest Neighbor，KNN）分类器和拉格朗日支持向量机（Lagrangian Support Vector Machine，LSVM）分类器来评价算法的性能。为更好地对面向层次化数据的在线流特征选择算法进行评价，使用四种评价指标对算法的性能进行分析，分别是：预测精度（Accuracy）、TIE、H-F1（Hierarchical-F1）和LCA-F1。

令D、分别表示样本真实类别和样本预测类别，Anc(D)表示类别D的所有祖先节点，Lac(D，)表示类别D，的最近公共祖先节点。D，的层次分类扩展标记分别为：。最小公共祖先节点层次分类扩展标记表示为：。

1）Accuracy 表示样本类别被正确划分的程度。

2）TIE 表示在层次结构中真实类别节点D和预测节点-D之间的总边数：

3）H-F1 表示分层准确率PH和召回率RH的调和平均：

4）LCA-F1 表示预测类别节点-D和真实标记节点D最小公共祖先：

以上4 个性能评价指标，TIE 指标取值越小越好，而Accuracy、H-F1 以及LCA-F1 的取值越大表明算法性能越佳。

3.3 参数分析

为观察参数k和δ在不同取值情况下对OH_ReliefF 算法的影响，令k=｛10，15，20，25，30｝，δ=｛0.000 1，0.001，0.01，0.1，1｝，在数据集AWA 和Bridges 上分别进行实验，观察OH_ReliefF 算法所筛选的特征子集在评价指标Accuracy、HF1、LCA-F1 和TIE 的结果，并结合算法运行的时间来选择最佳参数。OH_ReliefF 算法在不同参数下的效果性能表现如图2 所示。

对Accuracy、H-F1 和LCA-F1 这三个评价指标，在使用KNN 分类器（K=10）和LSVM（C=1）分类器时，从图2（a）、（b）可以看出，当k=20，δ=0.1 时，OH_ReliefF 算法在数据集AWA 上表现出的效果最佳，三个评价指标均略高于其他参数选项；当k=25，δ=0.001 时，各指标的结果为次优。从图2（c）、（d）可以看出，当k=25，δ=0.001 时，在数据集Bridges上表现出的效果最佳。

图2 参数k和δ的不同取值情况对OH_Relief算法的影响Fig.2 Influence of different values of parametersk andδ on OH_Relief algorithm

对TIE 这个评价指标，在使用上述两个分类器时，OH_ReliefF 算法在数据集AWA 上的结果相同，但当参数k=25，δ=0.001 时，数据集Bridges 在两个分类器上综合表现低于其他参数选项。

综合4 个评价指标，参数k=20，δ=0.1 和参数k=25，δ=0.001 使得OH_ReliefF 算法能取得较优的性能表现。而从图3 可以看出，k=25，δ=0.001 时所消耗的时间要少于k=20，δ=0.1 的情况。

图3 数据集AWA、Bridges在不同参数时的运行时间Fig.3 Running times of AWA and Bridges datasets at different parameters

从以上分析结果可以看出，在不同分类器的情况下，结合4 个性能评价指标和运行时间，算法OH_ReliefF 的性能在取k=25，δ=0.001 时表现最佳，因此在3.4 节的实验中取k=25，δ=0.001 进行实验。

3.4 实验结果分析

为有效验证OH_ReliefF 算法的有效性，本节实验选择5个当前现有的在线流特征选择算法作为对比算法，分别是：1）OSFS［8］，设置α=0.01，该算法此时达到最优效果；2）Fast-OSFS（简称FOSFS）［8］，设置α=0.01，该算法此时达到最优效果；3）OFS-Density（简称OFSD）［16］，设置α=0.05，该算法此时达到最优效果；4）SAOLA［17］，设置α=0.01，该算法此时达到最优效果；5）A3M［18］。

基于KNN 分类器(K=10)和LSVM 分类器(C=1)，本文在Accuracy、LCA-F1、TIE 比较本文算法与上述5 种算法，结果如表2～7 所示，加粗数字表示在不同评价指标中的最优结果，下划线表示次优结果；“↑”表示数值越大越好，“↓”表示数值越小越好。

根据表2～7 的结果可以看出：OH_ReliefF 算法在6 个数据集的3 个评价指标中的平均性能都排在第一。在KNN 分类器上，所提算法在3 个数据集（DD、F194、VOC）上表现出最优的效果，在Bridges 和Cifar 数据集中表现次优；在LSVM分类器上，数据集Cifar 表现出的结果为次优，其他5 个数据集的所有指标均是最优，在每个数据集上的分类性能较为稳定。

表2 基于KNN分类器的分类精度（↑）Tab.2 Classification accuracy based on KNN classifier（↑）

表3 基于KNN分类器的LCA-F1值（↑）Tab.3 LCA-F1 values based on KNN classifier（↑）

表4 基于KNN分类器的TIE值（↓）Tab.4 TIE values based on KNN classifier（↓）

表5 基于LSVM分类器的分类精度（↑）Tab.5 Classification accuracy based on LSVM classifier（↑）

表6 基于LSVM分类器的LCA-F1值（↑）Tab.6 LCA-F1 values based on LSVM classifier（↑）

选择A3M、OFSD 和OH_ReliefF 这三个算法在Bridges、DD 和F194 数据集上运行，算法在不同数据集上选择特征的个数如表8 所示。可以看出，算法A3M 和OFSD 选择的特征的个数过多或者过少，而算法OH_ReliefF 选择出的特征个数较为适中，所以在整个实验中，OH_ReliefF 在很多方面的性能均优于对比算法，在各个评价指标上均表现优异，相较于其他算法更加稳定。

表7 基于LSVM分类器的TIE值（↓）Tab.7 TIE values based on LSVM classifier（↓）

表8 不同算法在3个数据集上选择的特征个数Tab.8 Number of selected feature of different algorithms on three datasets

4 结语

本文基于ReliefF 算法提出了一个面向层次化数据的在线流特征选择算法OH_ReliefF。首先，将兄弟策略与排斥策略相结合对ReliefF 算法进行改进，定义一种新的能够处理层次化结构数据的ReliefF 模型；其次，根据特征的权值定义层次分类在线流特征选择模型框架，分为在线选择重要特征和在线冗余分析两个阶段；最后，与五种先进的在线流特征选择算法作对比，大量的实验结果表明本文算法OH_ReliefF在KNN 分类器和LSVM 分类器的各个评价指标中均取得了较优的结果。在未来的工作中，将对基于图结构的在线流特征选择算法进行研究。