双重特征加权模糊支持向量机
邱云志,汪廷华,戴小路
(赣南师范大学数学与计算机科学学院,江西赣州 341000)
0 引言
支持向量机(Support Vector Machine,SVM)[1-2]是基于统计学习理论提出的一种机器学习算法,旨在寻找一个最优分类超平面,根据有限的样本信息在模型的学习精度和学习能力之间寻求最佳折中。针对样本线性可分情况,通过把原始问题转化为凸优化问题求解;样本线性不可分时则应用了核技巧,解决了传统机器学习算法的维数灾难和局部最小问题。SVM 算法在解决小样本、非线性、高维模式识别中表现出了独特的优势,广泛应用于图像分类[3]、自然语言处理[4]、生物信息学[5]等领域。
关于常规SVM 算法的改进,研究学者们做了大量工作,提出了许多改进的SVM 模型。为了避免核函数被弱相关或不相关的特征所支配,文献[6]中提出了特征加权支持向量机(Feature-Weighted SVM,FWSVM)模型;为了克服样本中噪声或离群点的影响,文献[7]中提出了模糊支持向量机(Fuzzy Support Vector Machine,FSVM)模型,充分考虑到不同样本对分类超平面贡献的大小从而确定隶属度值,降低了噪声或离群点对分类性能的影响。后续的学者对于FSVM算法的关键问题,即隶属度函数的设计做了大量的研究:文献[8]中将隶属度的计算拓展到特征空间,在分类性能上有所提升;文献[9-12]中分别通过设计新的隶属度函数改进了常规FSVM 算法;文献[13]中综合考虑了特征权重与样本权重,在构造隶属度函数时应用了特征权重,提出了基于Relief-F 特征加权的FSVM 算法,但该算法仅仅是在计算隶属度时考虑了各个特征对样本到其所在类中心距离的影响。
为同时考虑特征加权对隶属度函数和核函数计算的影响,本文提出了一种新的模糊支持向量机方法——双重特征加权模糊支持向量机(Doubly Feature-Weighted FSVM,DFWFSVM)。首先通过信息增益(Information Gain,IG)度量每个特征的重要性程度,得到每个特征相应的权重。接着,一方面在隶属度函数的计算中,在原始空间中应用特征权重计算出样本到类中心的加权欧氏距离,从而基于加权欧氏距离构造隶属度函数;另一方面在样本训练过程中将样本的特征权重应用到核函数的计算中,从而避免弱相关或不相关的特征支配核函数的计算。实验结果表明,DFW-FSVM 相较于对比算法具有更好的推广性能。
1 相关理论基础
1.1 模糊支持向量机
不失一般性,本文以二分类问题进行FSVM 算法的理论分析,对于已知标签的训练样本集,其中xi∈Rn是原始空间中的样本点,yi∈{+1,-1}是类标签,si∈[0,1]是隶属度值,表示样本点xi归属于某一类yi的权重。FSVM 的目的是寻找一个能最大化分类间隔的分类超平面wTϕ(x) +b=0,其中w为一个垂直于分类超平面的法向量,b为位移量。相较于线性可分问题,对于非线性问题,通过映射ϕ将样本xi从原始空间映射到高维特征空间中,在特征空间中求解最优分类超平面的问题便可以转化成下面的最优化问题:

其中:ξ=(ξ1,ξ2,…,ξl)T是松弛变量,C>0 是正则化参数。
针对上面的最优化问题,通过Lagrange 乘子法求解,可以转化成下面的对偶问题:

其中:αi≥0 为拉格朗日乘子,表示内积。
通常并不知道映射ϕ的具体形式,也无需知道,根据式(2)可知只需计算内积的值,研究人员引入核函数k(xi,xj)把特征空间中的内积运算转化为在原始空间上进行简单的函数计算,解决了维数灾难问题。求得相应的决策函数为:

其中sign(⋅)是符号函数。
常用的核函数如下:
1)多项式核函数:

2)径向基核函数:

3)Sigmoid 核函数:

1.2 特征加权
特征加权一般指根据某种准则对样本中的特征赋予相应的权重。本文对于特征权重的值通过信息增益来度量。信息增益指信息熵与特征条件熵之差,其中信息熵作为度量样本集合纯度的指标,信息熵的值越大,样本集合的纯度越低。针对离散值和连续值特征的信息增益计算方法如下:
设样本集合D有m个类别标签Ci(i=1,2,…,m),|D|表示D中所有的样本的个数,|Ci,D|表示D中类别标签为Ci的样本个数。假定特征a有v个可能的取值aj(j=1,2,…,v),则样本集合D的信息熵定义如下:

如果是离散值特征,则可由下式表示用特征a对样本集合D进行划分所获得的信息增益Gain(D,a):

其中Dj表示样本集合D中在特征a上取值为aj的样本集合。
如果是连续值特征,通常采用二分法对连续值特征进行处理,首先对连续值特征升序排序,记为{a1,a2,…,av}。基于划分点t将数据集D划分为子集和,其中包含在特征a上取值不大于t的样本,则包含在特征a上取值大于t的样本,针对连续特征a,需要考察包含v-1 个元素的候选划分点集合,然后像离散值特征一样来考察这些划分点,选取最优的划分点进行样本集合的划分。可由式(9)表示用特征a对样本集合D进行划分所获得的信息增益Gain(D,a):
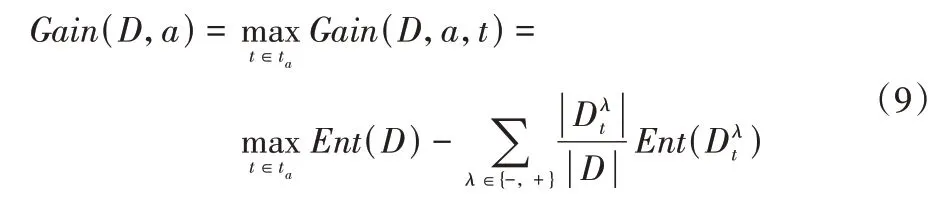
其中Gain(D,a,t)是样本集D基于划分点t二分后的信息增益。
通过这种方法可以计算出样本集合D中每个特征的信息增益,信息增益的值越大,表示该特征对于分类的贡献越大,因此求出的各个特征的信息增益可以代表各个特征的权重。
2 基于双重特征加权的模糊支持向量机
2.1 特征加权核函数
关于特征加权核函数的构造,本文以常用的三种核函数为例,根据式(8)和(9)求出特征权重=(1,2,…,n),则特征矩阵的对角矩阵的形式如下:

1)特征加权多项式核函数:

2)特征加权径向基核函数:

3)特征加权Sigmoid 核函数:

2.2 特征加权隶属度函数
欧氏距离作为应用最广泛的距离度量方式,简单易行,但标准欧氏距离对于每个样本的特征都赋予了相同的权重,然而实际情况并非如此,因此有些学者提出了特征加权欧氏距离的计算方法。两个样本xi和xj间的特征加权欧氏距离的计算公式如下:

其中:≥0(k=1,2,…,n)表示第k个特征的权重,n表示特征的个数。
本文设计隶属度函数时,考虑基于原始空间计算样本到其所在类中心的加权欧氏距离的大小:样本点到类中心的距离越小,表示该样本点的隶属度越大;反之,则表示该样本点的隶属度越小。下面以二分类数据为例设计隶属度函数。
设x+、x-分别代表正类和负类样本的n个特征上的均值点并作为正负类的类中心,分别代表正类和负类样本点到其所在类中心的加权欧氏距离,r+、r-分别代表正类和负类样本点距离其所在类中心的最远距离。

通过式(15)~(17)的计算可得出基于距离的隶属度函数表达式如下:

其中δ为事先给定的一个很小的正数用来保证si∈(0,1]。
2.3 算法设计
DFW-FSVM 算法的具体步骤如下:
输入 数据集S;
输出 预测标签。
1)数据集预处理并按照7∶3 的比例随机划分训练集与测试集;
3)构造加权隶属度函数,计算出每个样本的隶属度si;
4)构造特征加权核函数kp(xi,xj);
5)通过网格搜索寻找核函数参数γ和正则化参数C的最优值,训练FSVM 算法;
6)运用DFW-FSVM 算法进行预测,并进行相关性能评估。
3 实验与结果分析
本文的实验在i5 处理器、CPU 频率2.6 GHz、安装内存(RAM)8 GB、Windows 7 操作系统上进行,采用LIBSVM 工具箱的变体[14],为每个样本分配不同的权重,实验工具是Matlab R2015b。为了验证本文所提算法具有较好的性能,在UCI 机器学习数据库[15]中选取了8 个二分类的数据集,具体的数据信息如表1 所示,其中对数据集WBC,去除了16 个包含未知特征值的样本,剩下683 个样本。

表1 实验数据信息Tab.1 Experimental data information
本实验对所有数据均归一化到[0,1]区间,并按照7∶3的比例随机抽样划分训练集和测试集,核函数选择高斯核函数,通过网格搜索的方法寻找核函数参数γ和正则化参数C的最优值,其中C={2-5,2-3,…,215},γ={2-15,2-14,⋅⋅⋅,23}。
将本文算法与以下五种算法进行对比:
1)SVM:标准的SVM 分类算法[1-2]。
2)FSVM:标准的FSVM 分类算法,即在原始空间中基于样本点到类中心的距离计算隶属度的FSVM 分类算法[7]。
3)FWSVM:通过信息增益算法对标准的SVM 算法进行特征加权[6]。
4)FWFSVM:为了更好地与本文提出的DFW-FSVM 算法进行性能上的对比,通过用信息增益算法替换原算法中的Relief-F 算法,对标准的FSVM 算法进行特征加权[13]。
5)CKA-FSVM:基于中心核对齐思想设计隶属度函数的FSVM 分类算法[12]。
为了使实验结果更具说服力,本文使用准确率(Acc)和F1值(F1)作为对比各算法分类性能的评价指标。准确率是指分类正确的样本占样本总数的比例,是分类任务中最常用的性能度量;F1值是查准率(Precision,Pre)与 查全率(Recall,Rec)的调和平均。计算公式为:

其中:真正例TP(True Positive)表示正确分类的正类结果样本数,假正例FP(False Positive)表示错误分类的正类结果样本数,真反例TN(True Negative)表示正确分类的负类结果样本数,假反例FN(False Negative)表示错误分类的负类结果样本数。
六种算法的分类准确率和F1值的对比如表2 所示。可以看出,DFW-FSVM 算法在选定的8 个数据集上的F1值最高,并在7 个数据集上取得了最高的分类准确率,其中:在Ionosphere 数据集上,FWSVM 算法达到了与DFW-FSVM 算法一样的分类准确率;特别注意到CKA-FSVM 算法在非平衡数据集上取得了较好的效果,比如在Hepatitis 数据集上取得了最高的分类准确率,在CMSC 数据集上也取得了最高的F1值。

表2 六种算法在UCI数据集上的准确率与F1值对比 单位:%Tab.2 Comparison of accuracies and F1 values of six algorithms on UCI dataset unit:%
综合分析表明,在相同的条件下,DFW-FSVM 算法的性能有明显的提升。
1)当隶属度函数设计得不好时,模糊支持向量机会出现分类效果不如标准SVM 算法的情况,例如CKA-FSVM、FSVM和FWFSVM 算法在CMSC 数据集上的分类准确率低于SVM算法;FWSVM 算法在CMSC 数据集上的F1值低于SVM算法。
2)针对本文实验中的8 个数据集而言,特征加权思想有效地提高了算法的泛化性能,但是针对某些数据集也会存在特征加权失效的情况。比如在Hepatitis 数据集上,FWSVM算法虽然在F1值上优于SVM 算法,但是在算法分类准确率上反而低于SVM;反之,在CMSC 数据集上,FWSVM 算法虽然在分类准确率上优于SVM 算法,但是在F1值上却低于SVM 算法;在ST 数据集上,FWFSVM 算法在分类准确率和F1值上都低于SVM 算法。
3)DFW-FSVM 算法在上述8 个数据集上获得了比对比算法更好结果的原因可以从学习算法的鲁棒性加以解释,该算法通过获得的特征权重分别应用到隶属度函数和核函数的计算中,从而避免在计算过程中被一些弱相关或不相关的特征所支配,同时相较于单重特征加权算法,极大提高了算法的泛化性能,具有很好的推广性能。
4 结语
本文在分析基于特征加权的FSVM 算法的基础上,针对该算法只考虑特征权重对隶属度函数的影响,而没有考虑到在样本训练过程中将特征权重应用到核函数的计算上的缺陷,提出了基于双重特征加权的模糊支持向量机方法DFWFSVM。详细阐述了模糊支持向量机原理、特征权重的求解、特征加权核函数及隶属度函数的推导过程,并进一步通过实验验证了该算法可以改变特征空间中点与点之间的位置关系,避免在计算中被一些弱相关或不相关的特征所支配,表明了该算法能够较明显地提高分类器的泛化能力。由于本文算法只涉及单核的计算,因此下一步将考虑应用组合核函数以及如何改进隶属度的计算来提升分类器的性能。

