融合多粒度社区信息的网络嵌入方法
胡 军,许正康,刘立,钟福金
(1.计算智能重庆市重点实验室(重庆邮电大学),重庆 400065;2.重庆邮电大学计算机科学与技术学院,重庆 400065)
0 引言
现实生活中存在各种各样的网络,如社交网络、引文网络、蛋白质网络等。为了挖掘这些网络中的隐含信息,许多与复杂网络分析相关的算法被提出。由于网络数据属于非欧几里得类型,无法直接被较为成熟的机器学习算法进行处理,极大地阻碍了网络分析技术的发展。网络表示学习[1-2]通过将网络映射到低维特征空间中,从而可直接运用现有的机器学习算法对网络进行分析处理,是一种有效的对网络数据进行预处理的方法,已被应用到多个领域。近年来,在对网络表示的研究中,除了神经网络的方法[3-4]和基于矩阵分解的方法[5-6]外,基于Skip-gram 模型的网络表示方法也取得了较为不错的效果。它们使用随机游走(DeepWalk[7]、node2vec[8])或一阶、二阶近似(LINE(Large-scale Information Network Embedding)[9])可以很好地捕获网络中的局部结构信息,但忽略了一些隐含的全局信息,比如网络的社区信息。
为了将网络社区信息融合进节点表示中,一些学者提出了多种融合社区信息的网络表示方法[10-14]。这些方法的基本思想大都利用网络表示方法得到节点嵌入,使用聚类算法或社区发现算法获得网络的社区结构,再根据社区结构来更新节点嵌入。处理过程如图1 所示,首先将社区划分和节点嵌入整合得到每个社区的社区嵌入(三角和正方形节点),可视为虚拟社区中心节点,类似于节点嵌入,将社区嵌入定义为与节点嵌入有相同维度的向量形式;然后根据社区嵌入调整社区内节点的嵌入向量,使得原网络中有相同结构的节点在嵌入中相似的同时,在同一社区内的节点嵌入也表现为相似,即使这些节点没有直接联系。

图1 融合社区信息的网络表示Fig.1 Network representation by fusing community information
对于一个网络,根据不同的划分标准,可以得到不同的网络社区结构,并且网络的社区划分具有层次结构,即多粒度特性[15-16]。比如在校园社交网络中,如果按科系进行划分,可以形成多个不同的科系社团,但如果按学院来划分,多个科系就可以合并成一个学院社团,可见,不同的社团划分蕴含了网络不同粒度下的社区结构;然而,现有融合社区信息的网络表示方法大都只考虑单个粒度下的社团结构,损失了其他粒度下的社团结构信息。因此,在融合社区信息时有必要结合社区本身具有的多粒度特性,设计新的网络表示方法,保留更多原始网络中的信息(如图2 所示)。
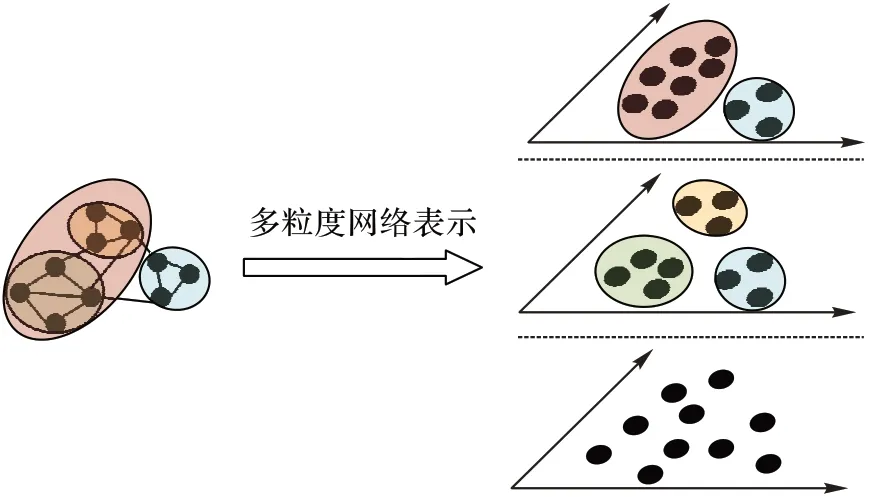
图2 多粒度网络表示Fig.2 Multi-granularity network representation
基于这一想法,本文提出了一种融合多粒度社区信息的网络表示方法(network Embedding based on Multi-Granularity Community information,EMGC)。本文的主要工作包括:
1)提出了一种社区嵌入的更新方法,将传统的社区发现算法和网络嵌入方法融合,得到不同粒度下的社区嵌入结果。
2)在不同社区粒度的网络中,将节点嵌入和社区嵌入进行优化,得到了融合相应粒度社区信息的网络嵌入结果。
3)在4 个真实网络数据集上的实验结果显示本文方法较其他对比方法能提升链接预测和节点分类等下游任务的准确率。
1 相关工作
网络表示学习近年来受到越来越多的关注,产生了许多相关方法。这些方法一般可以分为基于矩阵分解的网络表示方法[5-6]、基于神经网络的表示方法[17-20]以及基于Skipgram 模型的网络表示方法三种。在基于Skip-gram 模型的网络表示方法中,DeepWalk[7]最早将自然语言处理领域的词嵌入Word2Vec[21-22]中的思想引入到网络表示中,使用无偏随机游走得到节点序列,这些节点序列保留了网络的结构信息,通过Skip-gram 模型来训练这些节点序列,最终得到网络的嵌入表示;node2vec[8]在DeepWalk 的基础上使用深度优先和广度优先的搜索策略来控制随机游走,根据游走参数的不同,所得的节点序列蕴涵了网络的低阶和高阶结构信息;LINE[9]可以使得网络表示结果的同时保留网络节点的一阶近似和二阶近似信息。但这些方法都只考虑了网络的局部信息,忽视了全局信息。
由于网络中社区的重要性,一些学者开始考虑在网络表示时对社区信息进行保留。ComE(Community Embedding)[10]假设社区内的节点嵌入服从混合高斯分布,可以同时得到保留社区信息并符合高斯分布的节点嵌入结果;GEMSEC(Graph EMbedding with SElf Clustering)[11]能在学习节点嵌入的同时进行节点的聚类,最后获得保留类簇信息的嵌入以及高质量的聚类结果;CARE(Community Aware Random walk for network Embedding)[12]使用自定义随机游走,将社区内的节点按照一定概率插入到游走序列中,所得到的游走序列包含网络的局部结构信息和社区信息,再使用Skip-gram 模型得到最终的网络表示;CARA(Community Aware and Relational Attention)[13]在CARE 的基础上,使用图卷积网络(Graph Convolutional Network,GCN)[18]和注意力机制[19]捕获节点之间的语义信息;CNRL(Community-enhanced Network Representation Learning)[14]从概率推断的角度出发,对节点嵌入和社区嵌入联合优化,得到最终的节点嵌入、社区嵌入以及社区划分结果。但上述方法都只关注网络在某一个粒度层次的社区结构,没有考虑到社区的多粒度性质,损失了其他粒度层次所蕴含的社区结构信息。为此,有必要研究一种可以融合网络多粒度社区信息的表示方法。
2 融合多粒度社区信息的网络嵌入方法
2.1 定义
定义1网络。给定一个网络G(V,E,WV,WE),其中V={v1,v2,…,vn}是网络G的节点集合,E={eij}是网络G的边集,eij代表节点vi和vj所形成的边,m=|E|,WV=[wv1,wv2,…,wvn],WV∈Rn和WE=[weij],WE∈Rn×n分别代表网络节点权重矩阵和边权重矩阵。对于无权网络,可将网络节点权重和边权重设为1。
根据不同的社区划分标准,网络中的节点可以划分为不同粒度的社区结构。对于网络的一个社区划分C={c1,c2,…,c|C|},网络中的一个节点vi∈V,有社区分配函数z(vi)→C。
定义2多粒度社区。假设网络G可以划分成τ种不同粒度的社区结构,在t粒度下,网络的社区划分为Ct=,其中为t-1 粒度下的社区,并且在t粒度下,对于内部节点v都有zt(v)=。
定义3节点嵌入。在不同社区粒度下,对于网络G中任意节点vi∈V都有相应的节点嵌入∈Rd,t为当前社区粒度,d为网络嵌入的维度。
定义4社区嵌入。在不同社区粒度下,对于网络G中任意社区∈Ct都有相应的社区嵌入∈Rd,t为当前社区粒度,d为网络嵌入的维度。
2.2 节点嵌入
为了将网络结构信息融入节点嵌入,本文使用DeepWalk[7]来学习节点嵌入。DeepWalk 使用截断随机游走来捕获网络结构信息,得到游走路径集合S={s1,s2,…,sn},其中si={vi,…}表示以节点vi为起始节点的节点序列。对于节点序列si中任意节点,根据窗口大小生成中心-上下文节点对,并通过节点嵌入来刻画中心节点和上下文节点之间的关系。对于节点对(vi,vj),其中心节点vi预测上下文节点vj的条件概率为:

其中:vj是vi的上下文节点,ϕi、ϕ′j分别代表节点vi的嵌入以及节点vj的上下文嵌入。
根据Skip-gram 模型,DeepWalk 通过最大化中心节点预测上下文节点的条件概率,更新中心节点的嵌入。为了降低计算式(1)的复杂度,可以使用负采样策略将式(1)修改成如下的目标函数[21-22]:

其中:σ(x)=1/(1+exp(-x)),K为负采样的个数,Pn(v)为负采样的概率分布,通常Pn(v) ∝,dv为节点v的度数。
2.3 社区嵌入
为了确保网络嵌入能够保留网络的社区信息,本文根据所得到的网络社区结构来计算相应的网络社区嵌入。
2.3.1 社区发现
本文使用Louvain 算法[23]对网络进行划分,以此获得网络的多粒度社区结构。Louvain 是一种基于模块度优化的社区发现算法,通过最大化模块度来找到最优的社区结构,模块度的定义如下:

其中:m为网络中的总边数,weij为节点vi和vj之间的边权重,ki为节点vi邻接边权重总和,z(vi)为节点vi所在的社区,δ为Kronecker delta 函数。
依据式(3),将节点vi划分到社区c所产生的模块度增益如下:

其中:Σin为社区c内部边权总和,Σtot为与社区c有连接的边权总和,ki,in为节点vi与社区c内节点所连接边权总和。Louvain 算法通过遍历网络中所有节点,计算将节点划分到其邻居所在社区的模块度增益,并将其划分到最大正向增益的对应社区。
对于网络G(V,E,WV,WE),根据Louvain 算法首先得到网络的一个社区划分,其为原网络最细粒度的社区结构。根据得到的社区结构构造一个新的网络,并对新网络进行社区划分,从而进一步得到更粗粒度的社区结构。对于t-1 粒度下的网络,可以根据其社区划分Ct-1构建t粒度下的新网络,即将网络Gt-1中所有同一社区内的节点合并得到Gt中的一个节点,网络Gt-1中社区间若存在边,则在Gt对应节点间则构建一条边,同时将Gt中节点内部权重设置为合并节点集合内部权重的总和,即对于节点∈Vt,其权重为:

对于新得到的网络,按照之前的步骤可以得到新网络的社区划分。依此类推,直到模块度不再发生改变,可以得到原网络多个粒度下的社区结构。
2.3.2 嵌入更新
对于网络中的一个社区ci,将社区内的所有节点的嵌入进行平均,即得到相应的社区嵌入ψi,其计算公式如下:

其中:ϕj是节点vj的嵌入,|ci|为社区ci的内部节点数。


2.4 联合优化
在得到节点嵌入和社区嵌入后,本文利用社区嵌入来调整节点嵌入,使得调整后的节点嵌入可以保留网络的社区信息。基于节点与其所属社区的关系,节点的嵌入与其所属社区的嵌入在向量空间中应该相近。因此,可以通过计算节点与对应的社区之间的条件概率,将社区信息融合进节点嵌入当中:

其中cj是vi所属的社区,即z(vi)=cj。
对于采样网络中的节点vi,通过z(⋅)找到其所属社区cj,得到样本(vi,cj)进行训练。类似地,可以通过负采样优化策略来降低复杂度,其联合优化的目标函数为:
国家推行总额预付制的医保改革政策,其目的是为了倒逼医院规范医疗行为,控制医疗费用。现阶段,大部分医院在医保控费方面采用了分科定额控制管理方式,精细化程度不够。在新的医疗改革大环境下,迫切需要医院管理人员运用精细化管理的思维进行医疗费用的管控,在支持国家医改政策的同时,谋求医院自身的可持续发展。医院应探索多种医保费用管理手段,除了绩效考核方法以外,探索单病种质量管理及费用管控、临床路径管理等考核制度。

与节点嵌入不同,联合优化对社区进行负采样,以此确保所采样的社区不是节点vi所属的社区。
对于一个节点vi,节点在粒度层次t的嵌入是ϕti,则该节点嵌入ϕi为所有社区粒度下节点嵌入的拼接,即:

其中符号⊕为拼接运算。
本文方法框架如图3 所示,首先通过Louvain 算法得到多粒度社区结构;然后在不同的粒度下学习其社区嵌入,调整相应的节点嵌入,使之保留相应的社区信息;最后将融合不同粒度社区信息的节点嵌入拼接得到最终节点嵌入,相应的算法如算法1 所示。

图3 融合多粒度社区信息网络嵌入Fig.3 Network embedding based on multi-granularity community information
算法1 融合多粒度社区信息网络嵌入方法(EMGC)。
输入 网络G(V,E,WV,WE),嵌入维度d,节点游走次数λ,游走长度l,窗口大小w,负采样个数nneg;
输出 节点嵌入ϕ。

算法的第1)行使用Louvain 算法对网络进行社区发现,得到不同粒度下的社区结构;2)~3)行对原始网络进行随机游走,并根据式(2)初始化节点嵌入向量;4)~8)行根据不同粒度的社区结构迭代更新社区嵌入,联合优化节点嵌入向量。对于不同社区粒度下网络Gt,第5)行根据Gt中的社区Ct和ϕt-1使用式(8)更新Gt的社区嵌入ψt;第6)行根据ϕt-1和ψt使用式(10)来联合优化当前粒度网络的节点嵌入ϕt;第7)行使用式(11)拼接不同粒度下节点嵌入,得到最终的节点嵌入ϕ。
Louvain 算法的时间复杂度接近于O(m+n)。对于节点嵌入部分,通过随机游走进行节点嵌入,则该部分的时间复杂度为O(λ⋅l⋅n)。社区嵌入更新部分的时间复杂度与当前的社区数有关,算法执行过程中社区数最大为n,也就是原始网络节点数,所以社区嵌入更新部分的时间复杂度最大为O(n)。对于节点嵌入和社区嵌入的联合优化部分,只需要采样节点进行训练即可,则每次联合优化部分的复杂度为O(n)。因而算法1 的时间复杂度为O(m+n+λ⋅l⋅n+τ×(n+n)),线性接近O(m+n)。
3 实验分析
为了验证本文方法的有效性,本章分别在链接预测和节点分类任务上将本文方法与4 种典型的基于Skip-gram 模型的网络表示方法进行了对比,分别是DeepWalk、node2vec、ComE 和GEMSEC,其中前2 种方法只考虑了网络的结构信息,后2 种方法同时考虑了网络的结构信息和社区信息。实验中使用了4 个数据集,分别是Facebook[24]、Cora[25]、Wiki[26]和DBLP[10]。具体信息如表1 所示,包括网络的规模(节点集|V|、边集|E|)以及真实社区数|C|。

表1 数据集信息Tab.1 Dataset information
在实验中,本文提出的EMGC 的参数设定为:节点游走次数λ=5,游走长度l=80,窗口大小w=10,另外负采样个数nneg设置为10,为了避免拼接后嵌入向量维度过大,本文将嵌入维度d设置为16。node2vec 的参数p、q的取值范围设定为{0.25,0.5,1,2,4}。ComE 和GEMSEC 的社区数都设置为相应数据集的真实标签数。由于Facebook 没有真实标签,在这个数据集上的社区数设置为Louvain 算法发现的社区数。
3.1 链接预测结果分析
实验中,首先删除网络中部分存在的边,然后通过删减后的网络训练模型得到网络嵌入的结果,最后通过分类的方法来预测网络中丢失的边。对于每个网络,从中随机选择10%、20%、30%、40%、50%的边进行删除,并保证删除后的网络仍是连通的。这些被删除的边当作正例,同时在选取相同数量不存在的边当作负例。由于链接预测的预测对象是边,所以需要得到每条边对应的特征。通过对边的两个端点的嵌入向量求Hadamard 积,将得到结果当作边的特征进行预测。实验使用AUC(Area Under Curve of ROC)作为评价指标。在4 个数据集上取得的实验结果分别如表2~5 所示。

表2 Facebook上的链接预测的AUC结果 单位:%Tab.2 AUC results for link prediction on Facebook unit:%
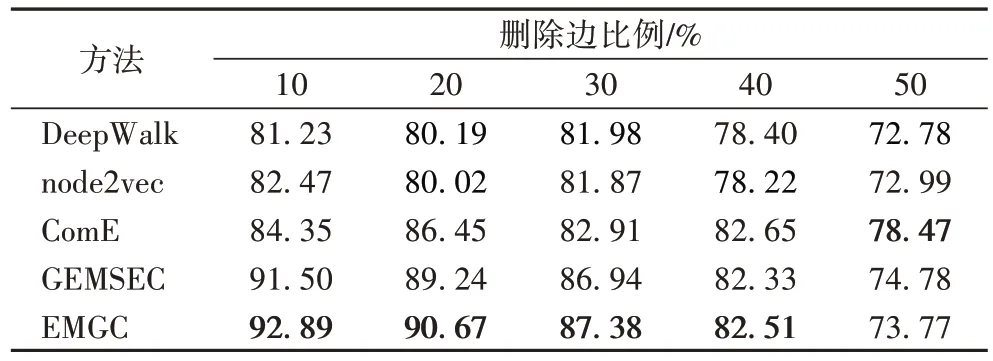
表3 Cora上的链接预测的AUC结果 单位:%Tab.3 AUC results for link prediction on Cora unit:%
从实验结果可以看出本文提出的EMGC 方法在多数情况下所取得的结果相较于其他未考虑的社区信息的方法(DeepWalk、node2vec)有较大的提升,而对于其他考虑了单一粒度社区信息的方法(ComE、GEMSEC)也有一定的提升。从结果中还可以观察到,同时保留结构信息和社区信息的方法比只保留了结构信息的方法在结果上表现更好,另外,EMGC 在稠密网络(Facebook)中比其他对比方法表现较好,而在较为稀疏的网络(Cora)中,随着网络中边的删除比例增加而预测精度有较大程度的下降。在Cora 网络中删除50%的边后,EMGC 所取得的结果有明显的下降,原因是在稠密网络上删除边并不会导致网络的结构发生大量改变,特别是对于网络社区结构,而在稀疏网络中删除过多的边会使得网络的社区发生明显变化,这使得社区发现划分的社区与真实社区有着较大的差异。另外Wiki 网络中在删除30%、40%、50%的边后,本文方法所取得结果与最好的对比方法相比略低,但相差的幅度不大。Wiki 数据集是多标签数据集,本文所使用的Louvain 算法是非重叠社区发现算法,所划分的社区并不能完全符合真实情况,随着删除边的比例增加,EMGC 社区发现结果的质量会随之降低,使得嵌入的预测精度处于同样的下降趋势。社区信息的大量损失会导致融合社区信息方法取得相对较低的结果,但总体上比只考虑局部结构信息的方法仍有着不错的提升。

表4 Wiki上的链接预测的AUC结果 单位:%Tab.4 AUC results for link prediction on Wiki unit:%

表5 DBLP数据上的链接预测的AUC结果 单位:%Tab.5 AUC results for link prediction on DBLP unit:%
3.2 节点分类结果分析
节点分类的目标是将网络中未标记的节点划分到单个或多个类别当中。由于Facebook 数据集没有真实标签,Wiki为多标签数据集,所以本文选择在稀疏网络Cora 和稠密网络DBLP 上进行实验验证。在这两个数据集上,随机选择10%~90% 标记节点当作训练样本来训练一对多分类器(OneVsRest)分类器。对于每种分类实验,都执行10 次,计算Macro-F1 和Micro-F1 的平均值来评价网络嵌入结果的有效性。
在Cora、DBLP 数据集上进行节点分类所取得结果分别如表6、7 所示,每列粗体数字代表取得的最好结果。在Cora数据集上,当训练比例小于30%时,node2vec 取得最好的结果,而当训练比例增大时,EMGC 取得的结果始终比其他方法好。相同的结论在DBLP 数据集上也有体现,这是由于本文方法的节点嵌入是进行拼接得到的,其包含的特征维度较大,训练分类器需要更多的样本进行训练以获得最佳的分类器性能。另外,在DBLP 数据集中,当训练比例为60%或70%时,本文方法取得的Micro-F1 比node2vec 稍低,处于可接受的范围,同时node2vec 取得的Macro-F1值比本文方法低,但相差不大,即在60%或70%的训练比例时,node2vec 可以得到与本文方法接近的结果。总体上,与其他对比方法相比,随着训练比例的增大,本文提出的EMGC 方法能够取得较好的分类精度。

表6 Cora数据集上的节点分类结果 单位:%Tab.6 Node classification results on Cora dataset unit:%

表7 DBLP数据集上的节点分类结果 单位:%Tab.7 Node classification results on DBLP dataset unit:%
3.3 粒度分析
为了分析不同粒度对结果的影响,本节通过拼接不同粒度下的嵌入,分别在链接预测和节点分类实验的基础上,研究其对预测结果的影响。在链接预测的实验中,随机删除50%的边,使用AUC 作为评价指标。在4 个数据集中,不同拼接粒度所预测的结果如图4 所示。

图4 4个数据集上不同粒度的链接预测结果Fig.4 Link prediction results of different granularities on 4 datasets
在节点分类的实验中,使用50%的节点进行训练,使用Macro-F1 和Micro-F1 进行评价。不同拼接粒度下的节点分类结果如图5 所示。所有实验中的每个粒度下的嵌入都是与之前所有粒度下的嵌入进行拼接得到。
从实验中可以发现,Cora、DBLP 被划分为6 个粒度,Facebook 被划分为4 个粒度,Wiki 被划分为5 个粒度。从链接预测的结果(图4)中可以看到,在所有的数据集上,使用2层粒度拼接的嵌入进行预测可以取得最大值,而之后随着拼接粒度的增加,除了DBLP(图4(b))上结果基本稳定的情况外,在Cora(图4(a))、Facebook(图4(c))、Wiki(图4(d))上取得链接预测结果处于下降的趋势。相同的结果也可以从节点分类的结果(图5)中看到,在Cora(图5(a))、DBLP(图5(b))上的Micro-F1 和Macro-F1 在粒度为2 时可以取得最大值。随着拼接粒度的增加,分类结果开始波动,总体上呈下降趋势。因此,2 层粒度的拼接是最优选择,拼接过多的粒度反而会使得实验结果的精度下降。

图5 2个数据集上不同粒度的节点分类结果Fig.5 Node classification results of different granularities on two datasets
3.4 时间消耗
为了验证算法在时间复杂度上的优势,本节将比较所提出的算法与其他对比方法上在4 个数据集上进行嵌入所消耗的时间。由于对比方法中DeepWalk、node2vec、ComE 与EMGC 的实现方式不同,这里只与相同实现方式的GEMSEC进行比较。EMGC 和GEMSEC 的运行时间如图6 所示。
从图6 中可以发现,与GEMSEC 相比,在Cora、DBLP 和Wiki 数据上,EMGC 的运行时间都低于GEMSEC,而在Facebook 数据集上,EMGC 的运行时间略高于GEMSEC,但只有不到1 s 的差距,两者相差不大。结合表1 可以看出,EMGC 在不同数据集上的运行时间与该数据集中的节点个数有着很大关联,这与算法复杂度分析结果相一致。
4 结语
为了在网络表示中保留更多原始网络中的隐含信息,本文提出一种融合多粒度社区信息的网络嵌入方法。该方法使用Louvain 算法对网络中的社区进行划分,得到不同粒度下的社区结构;根据不同粒度下的社区结构,在训练节点嵌入的同时计算相应的社区嵌入,利用社区嵌入更新节点嵌入,使得节点的嵌入结果在保留网络局部结构信息的同时,保证社区内节点的嵌入与对应的社区嵌入结果相似;将不同粒度下得到节点嵌入进行拼接,最终得到融合多粒度社区信息的网络嵌入结果。在4 个真实网络上进行的实验结果表明本文提出的方法能够保留更多的原始网络的信息,从而提升后续链接预测和节点分类的准确率。
本文中社区发现结果对最终的嵌入结果有着重要影响,文中提出的算法所针对的是非重叠社区,而现实中的社区有很大一部分为重叠社区结构,对于未来的工作,将考虑改进嵌入方法,使之能够应用于重叠社区的网络场景中。

