创设课堂亮点，突破教学重难点

■天津市静海区模范小学 刘 锦

课堂是教学的“主阵地”，课堂中的重点、难点就是这阵地中的“堡垒”，攻克“堡垒”的方法是教学成功的关键。选择恰当的方法突破重难点，可以使学生更容易理解与掌握知识，学生的思维会更活跃，课堂会令人眼前一亮。

一、借助生活情境，突破重难点

数学源于生活，在教学中我们尽可能地将数学知识融于生活中，利于学生体验与理解，达到借助生活情境点亮课堂的目的。

例如：在学习“乘法分配律”的时候，学生经常出现（a+b）×c=a×c+b这样的错误，其实就是学生没有理解“分别”是什么意思。针对这个问题，笔者创设了贴近学生生活的情境，并让学生进行表演：a同学和b同学是好朋友，新来的c同学也想和两人做朋友，所以c同学和两个人分别握手，也就是c同学先和a同学握手，再和b同学握手，大家快快乐乐在一起。学生通过表演生活中的情境，直观、形象地落实重点、突破难点。

课堂中利用学生熟悉的生活情境，把数学问题生活化，不仅激发了学习兴趣，而且益于学生对重难点的理解和掌握，学生最大的变化就是从厌学到乐学。

二、找准新知的生长点，突破重难点

新课程理念明确强调：“数学教学必须以学生的认知发展水平和已有的经验为基础。”在教学时，教师必须遵循新课程理念，找到新知的生长点，帮助学生解决新问题。

1.找到“原型”，以旧启新。

这里的原型是指与新知有相似之处的旧知，它是新知的最佳生长点，找准旧知感悟新知，促进新知的顺利建构。

例如：在教学“三角形高的画法”时，根据以前的教学经验，这部分知识既是这节课的重点，又是这节课的难点，因为学生不知道这个新知的生长点是什么，也就是不知道它的原型是什么。在教学时，笔者利用课件演示把三角形的另外两条边隐去，学生发现原来是前面学习过的直线外一点做这条直线的垂线的知识。通过以上教学，学生就会觉得新知并不“新”，教学重点和难点也就突破了。

2.抓住“冲突”，以旧探新。

在教学时，抓住与新知识密切联系的相关知识经验，在认知冲突中来探究新的问题，体验成功的快乐。

例如：教学“两位数乘两位数的笔算乘法”时，放手让学生尝试计算14×12。在这里学生思维发生碰撞，呈现出拆数的方法（把12拆成6乘2）、口算的方法、竖式的方法等多种计算方法。在教学竖式的方法时，有部分学生想到了两位数乘一位数的竖式计算，试着迁移到两位数乘两位数的计算中来，但在计算中出现了图1这种错误。

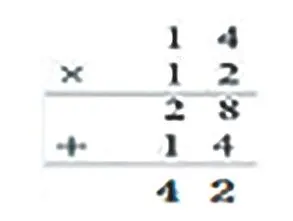
图1

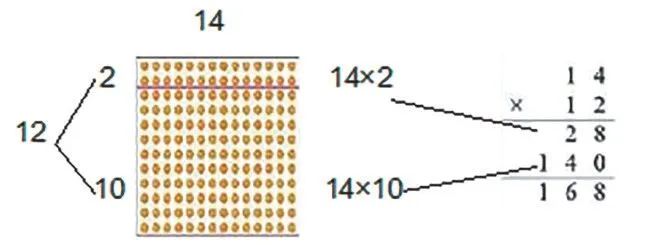
图2

这时让学生充分表达“哪里是正确的，利用了什么知识”。有的学生把竖式中的第二个乘数中的十位遮挡，就变成了两位数乘一位数的笔算，其他学生一目了然；有的学生发现竖式中的14×2=28这一步，就是口算中的第二步。接着追问：“你认为哪里有问题，应该怎样解决新的问题，为什么这样解决？”这时有一个学生用写有0的卡片把竖式中第二个乘数中的个位遮挡，并结合口算的方法说明笔算第二步应该是计算14×10=140，结果应该是140，而不是14，学生清楚地知道了这一步是求10个14是多少，进而知道了卡片上的0是隐藏的，所以140中的0可以隐藏起来。甚至有的学生看到了这一步与两位数乘一位数的计算方法是一样的，就是计数单位不一样，计算的结果应该是14个十，其中的4要与第二个乘数的十位对齐。学生用旧知来探究新知，理解了两位数乘两位数笔算乘法的算理。最后借助点子图引导学生深入地剖析（见图2），将口算方法和笔算方法及其点子图进行对比，找到它们之间的联系，直观、形象、清楚地理解了算理，学生感受到成功的体验。

在以上教学中，学生发现这几种方法从内容到形式之间的实质性的联系，抓住冲突以旧探新，突破了教学重难点，也为后面学习三位数乘两位数的乘法打下良好基础，“明其理，得其法”的教学过程体现了单元整体教学的作用。

三、利用动手实践，突破重难点

动手实践是学习数学的重要方式，可以让学生在动手操作的过程中亲身经历知识的形成过程，从而领会新知识，这样促进学生获得对数学知识的理解，进而突破教学重难点。

例如：在教学“面积单位”时，当学生认识了1平方厘米、1平方分米后，可以顺势迁移出边长为1米的正方形面积是1平方米，但学生对1平方米实际大小的感知是模糊的。为了让学生亲身经历知识的形成过程，真正感悟1平方米的大小，教师在小组中为每人准备一根1米长的绳子，四个人拼出一个1平方米的正方形。这时有的小组通过摆一摆，在地上拼成了一个1平方米正方形；还有的小组通过拉一拉，围成了一个1平方米的正方形。学生通过动手操作不仅知道了什么是1平方米，而且感悟到1平方米有多大。在学生的头脑中建立了1平方米到底有多大的表象，达到从“一维”的长度走向“二维”的面积的思维蜕变，发展了学生的空间观念，培养了学生的量感。

学生在动手实践中把数学知识变得简明、形象，易于理解，真正感知了知识，教学重点和难点也随之突破。这充分体现了“知识固然重要，但方法比知识更重要”，这也是数学课堂教学中最需要做的事之一。

四、通过思考建构，突破重难点

由于数学概念具有高度的抽象性和概括性，教学时应尽可能地为学生提供充分的感知材料，引导学生进行探索，在探索中思考，在思考中建构，从而达到认识概念本质的目的。

例如：在教学“三角形的概念”时，学生找到生活中的三角形，然后从这些物体中抽取出三角形，并观察这些三角形，找到它们相同的地方，从而知道三角形具有三条边、三个角、三个顶点的特征。再通过出示不同的图形（见图3），让学生具体判断哪个图形是三角形，从而逐步抽取出三角形的概念。

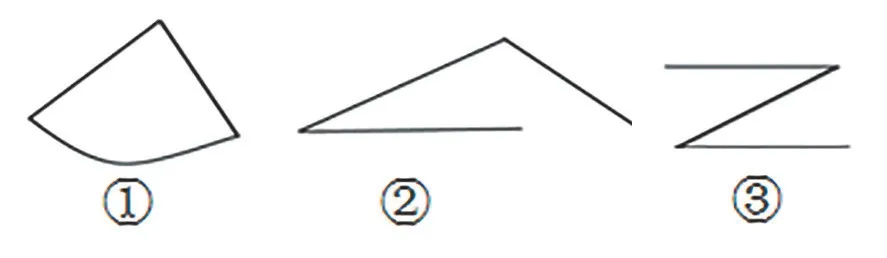
图3

在判断①号图的时候，有的学生说有一条边不是直线，所以它不是三角形，有的学生反驳说是有一条边不是线段。在思维的碰撞中，学生明白三角形的三条边是三条线段，教师利用课件演示把弯曲的线拉直变成一条线段，利用形象的画面帮助学生加深理解。判断②号图的时候，学生认为它没封口不是三角形，教师根据学生发言利用课件演示将三角形封口，突出“首尾相连”。判断③号图的时候，学生进一步理解“首尾相连”就是“围成”。根据学生发言，教师总结出三个图形不是三角形的原因，依次概括出“三条线段”“封闭图形”“首尾相连”也就是“围成”，继而揭示出三角形的概念。接下来让学生用自己身边的材料围出三角形，通过三角形的特征来检验所围成的三角形是不是规范，从而再次强化三角形的概念。

学生在过去的教学中只知道三角形的概念是什么，并不知道为什么要这样定义。现在的教学借助图形的直观性引发数学思考与探索，逐步建构，让学生真正感悟到数学的本质，进一步培养了学生的数学素养。

“教学有法，但无定法，贵在得法。”在教学中如何突出重点、突破难点也没有固定的方法，只要我们多思考“教什么”“怎么教”“为什么这样教”，再结合自己的教学艺术和智慧，重难点的突破就会水到渠成，学生就能体验到数学的魅力，增强他们对数学知识的应用意识。