基于探地雷达的混凝土空洞病害正演研究
芦俊伟 ,张如祥, 王 迪 ,程泉森, 陈丹帅
(1.石家庄铁道大学电气与电子工程学院,河北 石家庄 050043;2.石家庄铁道大学机械工程学院,河北 石家庄 050043)
国民经济的稳步发展与愈加完善的交通基础设施密不可分,根据交通运输部在国新办新闻发布会上的发言,截至2020年底,我国高速公路对20万以上人口地区的覆盖率超过98%,高速铁路对于百万以上人口城市的覆盖率达到了95%。与此同时,作为基础设施中应用最为广泛的钢筋混凝土结构,易受到地质水文、列车荷载等因素的影响而出现裂缝、脱空等病害,严重危及设施运行安全。这就需要更加快速高效且能为病害检修提供精准依据的无损检测手段,目前钢筋混凝土结构内部病害的无损检测方法主要包括超声波法、冲击回波法、探地雷达法等。其中超声波法在空气介质中衰减速度较快,检测时需与混凝土表面紧密贴合,不适用于车载检测方式;冲击回波法激励源通过人工敲击获得,检测速度较慢;相较于其他无损检测手段,探地雷达具有精度高且能够连续检测的优点,采集到的回波数据更加直观地表明了钢筋混凝土结构内的布筋情况及病害与否,且节省了时间及人力成本。
但在实际的探测过程中,探地雷达数据采集易受到探测表面平整度、结构内部复杂程度等因素的干扰,采集到的回波数据往往会有道数缺失或信噪比较低的问题,不利于雷达数据的处理及解释,所以把握好多种外部及内部条件下病害的成像规律尤为重要。对此陈婕对不同大小、不同形状、不同埋深的隧道衬砌空洞模型进行了构建,运用gprMax3.0软件对模型正演,总结了不同空洞尺寸、形态、位置下的空洞回波特征;尹光辉针对道路路基在发生充气或充水空洞病害时的情况进行了数值模拟,分析了空洞内部介质对于回波图像的影响;刘涛将隧道衬砌结构内不同病害在不同频率波源下的正演结果进行了对比,以求找到可用于区分识别回波图像中不同病害的特征依据。但这些研究大多只对病害模型进行了构建,而对结构本身性质以及钢筋回波的干扰提及较少。
针对上述问题,文章在充分考虑了混凝土内部介质复杂程度的基础上构建了不同介电常数及电导率下的空洞病害模型,分析了混凝土本身性质对于其内空洞回波的影响;另外根据钢筋干扰下的空洞病害仿真结果分析了钢筋直径及间距对于空洞病害回波的影响规律。
1 gprMax3.0软件正演原理
gprMax3.0软件基于时域有限差分法求解麦克斯韦3D方程,以时间步长递推计算电场和磁场的传播规律以及它们在介质空间上的分布,以模拟电磁波在不同介质下的传播。
1.1 麦克斯韦旋度方程
麦克斯韦方程揭示了电磁波在空间传播过程中电场与磁场之间的关系,包含两个旋度方程与两个散度方程,时域有限差分法基于麦克斯韦旋度方程:

其中,E为电场强度(V/m);D为电通量密度(C/m2);H为磁场强度(A/m);B为磁通密度(Wb/m2);J为电流密度(A/m2);为磁流密度(V/m2)。
1.2 3-D时域有限差分法基本原理
令f(x,y,z,t)代表E,H在直角坐标系中的任意一个分量,时域及空间域中的离散符号取为:
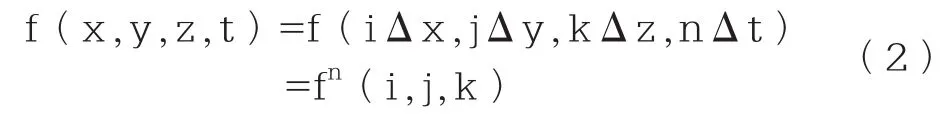
其中,Δx代表x方向空间步长,Δy代表y方向空间步长,Δz代表z方向空间步长,Δt代表时间步长,i,j,k分别代表x,y,z三个方向的空间步长个数,n代表时间步长个数。
利用中心差分的方法对式麦克斯韦旋度方程在直角坐标系中的展开式进行离散得到离散化电场及磁场的空间排布,建立合适的网格剖分体系,据此1966年正式提出了yee元细胞的概念,在时域有限差分离散场中电场与磁场的节点在直角坐标系中的空间排布如图1所示。

图1 FDTD离散中的Yee元胞
2 模型的建立及仿真结果分析
当钢筋混凝土结构当中出现空洞时,探地雷达回波可由如下模型构成:

其中,Rr,Rv,Rd,Rn分别代表钢筋回波、空洞回波、直达波、随机噪声,且钢筋回波与空洞回波统称为目标回波。其中随机噪声常通过对正演结果加入高斯噪声获得,文中暂不考虑加入随机噪声后的回波分析。
2.1 不同钢筋间距下的多目标回波分析
多目标回波状态下需考虑钢筋与空洞距离较近时,钢筋回波对空洞回波造成的影响。不同的混凝土结构其内部钢筋布设间距也不同,为研究钢筋间距对于空洞回波的影响,首先控制钢筋直径为6 mm,埋深0.2 m,空洞大小为0.4*0.05(m),埋深0.3 m,其次设置钢筋间距分别为0.1 m,0.2 m,0.4 m。模型对应的仿真结果如下:

图2 不同钢筋间距下的仿真回波图
显然,在钢筋的影响下,空洞回波受到了不同程度的干扰,且随着钢筋间距的增大,空洞回波逐渐明显化,由此可推断,其他条件不变的情况下,钢筋间距越大,空洞回波能量越大。
为验证以上说法,对三种布筋间距下的空洞模型单道正演结果进行了提取,图3(a)为经过直达波去除之后的第188道A-SCAN回波图,经计算,图中椭圆部分即为空洞回波的波峰位置,如图所示,钢筋间距越大,空洞回波幅值越大,在钢筋间距分别为10 cm,20 cm,40 cm时,空洞回波能量分别为1.7×10-3v/m,2.5×10-3v/m,4×10-3v/m。
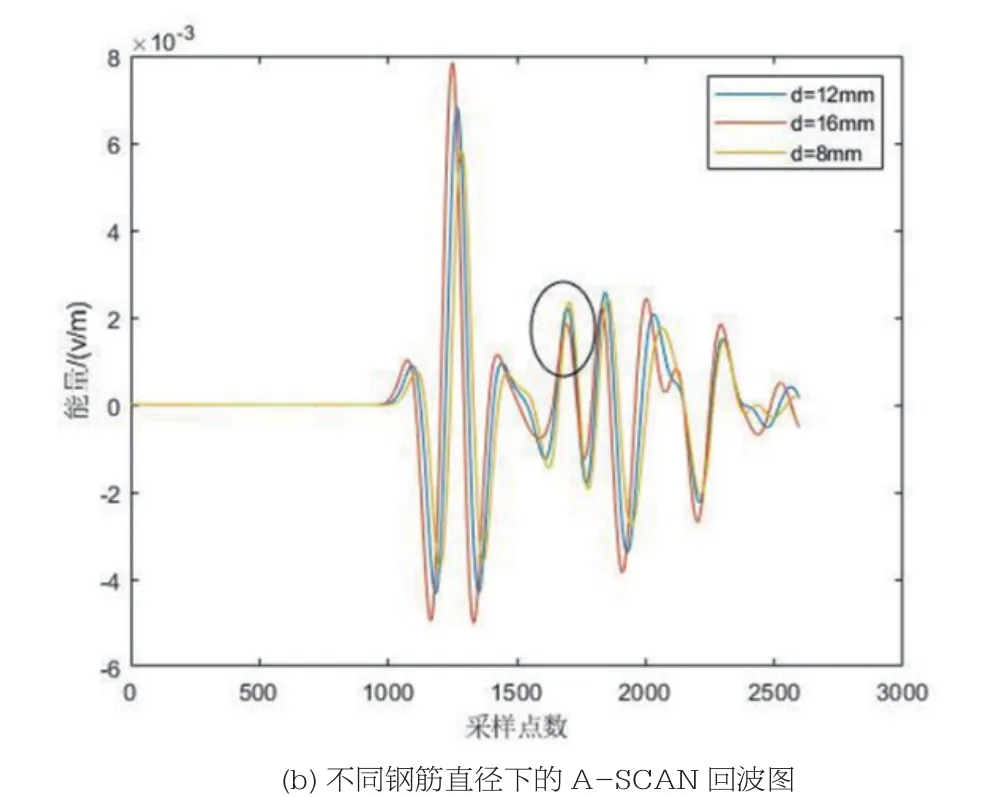
图3 不同钢筋间距及直径下的空洞A-SCAN回波图
2.2 不同钢筋直径下的多目标回波分析

首先控制钢筋埋深0.2 m,钢筋间距0.2 m,空洞大小为0.4*0.05(m),埋深0.3 m;其次设置钢筋直径分别为8 mm,12 mm,16 mm。模型仿真结果如下:

图4 不同钢筋直径下的仿真回波图
由空洞左右边缘回波的可见性分析得出:随着钢筋直径的增加,空洞回波越来越不明显,到钢筋直径16 mm时,在视觉上基本未见空洞回波,可见钢筋直径越大,空洞回波能量越小。
为验证以上说法,对三种钢筋直径下的空洞单道回波进行了提取,图3(b)为经过直达波去除后的第175道A-SCAN回波图,如图中椭圆位置即为空洞回波波峰位置,在钢筋直径分别为8 mm,12 mm,16 mm时,空洞回波振幅分别为2.29×10-3v/m,2.14×10-3v/m,0.18×10-3v/m,随着钢筋直径的增大,空洞回波能量越来越小。
3 结论
钢筋的存在对于空洞回波的影响是探地雷达数值仿真不容忽视的问题,文章利用gprMax3.0软件对不同钢筋直径、不同钢筋间距下的空洞病害进行了正演模拟,分析了这些因素的变化对于空洞回波的影响,得出以下结论:
在钢筋埋深、钢筋直径、空洞大小等因素不变的条件下,在仿真时设置的钢筋间距0.1~0.4 m之间,钢筋间距越大,对空洞回波的影响越小,也即空洞回波的能量随着钢筋间距的增大而增大。
在钢筋埋深、钢筋间距、空洞大小和位置等因素不变的条件下,在仿真时设置的钢筋直径8~16 mm之间,钢筋直径越大,对空洞回波的影响越大,也即空洞回波的能量随着钢筋直径的增大而减小。

