基于PCA-GA-BP 神经网络的秦岭北麓周至—蓝田段山前地质灾害危险性预测

刘育林, 周爱红, 孟维高

河北地质大学 城市地质与工程学院 , 河北 石家庄 050031

0 引言

地质灾害是指在自然或人类活动的影响下, 导致生命财产损失、 生态环境破坏的地质作用或现象。 而我国目前地质灾害发育的基本特点主要有类型多、 灾种全、 频率高、 损失大、 分布广。 所以对地质灾害进行准确预测是我国当前的必要工作。

国内外的专家学者提出了众多针对地质灾害危险性预测的方法。 国内目前对于地质灾害危险性预测研究的主要理论和方法有支持向量机[1][2]、 决策树[3][4]、 灰色关联度法[5][7]、 人工神经网络[8][9]等。尽管上述方法在各类地质灾害危险性预测中取得了一定效果, 但在某些方面仍然存在弊端。 如支持向量机在面对大规模、 高维数据时效果不佳。 参数和核函数选取的不同对预测结果影响较大; 决策树在对缺失值处理时, 功能有限。 因此, 需要较大的样本数据量;灰色关联度主观性过强, 不适用于波动较大的数据;人工神经网络收敛速度较慢, 容易导致局部最优, 影响预测结果正确率等。

基于以上分析, 本文以秦岭北麓周至-蓝田段山前地质灾害危险性为研究对象[10]。 由于影响地质灾害危险性的指标众多, 并且某些指标间具有很大的相关性。 因此本文首先使用主成分分析(PCA) 对影响研究区地质灾害危险性的影响指标提取主成分, 剔除各指标之间的线性关系, 然后结合具有全局搜索能力的遗传算法(GA) 算法优化BP 神经网络模型中参数。 最终建立基于PCA-GA-BP 的地质灾害危险性预测模型, 并应用于秦岭北麓周至-蓝田段山前地质灾害危险性预测中。

1 数据处理方法描述

影响地质灾害危险性的指标通常较多, 且不同指标间往往会存在一定相关性, 势必会增加分析问题的复杂程度, 进而影响研究结果的准确性。 所以,本文使用主成分分析法对原始指标进行降维, 从而达到消除指标间的相关性的目的。 具体流程: 首先利用主成分分析法对原始指标进行分析, 得到全部主成分及其特征值、 贡献率。 然后通过各主成分的累计贡献率确定本文所需的主成分。 最后利用各指标的得分系数对其重新组合, 生成一组新的主成分来代替原来的指标, 这些新产出的主成分能够反映原始指标的大部分信息, 并且主成分之间线性无关。其计算原理如下:

1.1 原始数据标准化

设原始数据矩阵为:

通过(2) 式求得标准化矩阵X*。

1.2 计算指标相关系数矩阵

由(3) 式可求得指标的相关系数矩阵R。

1.3 计算指标特征值矩阵

通过相关系数矩阵R的特征方程| R - λIP| =0,得出P个特征根。

1.4 确定主成分

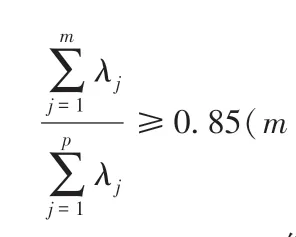
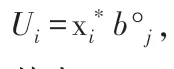
其中:U1: 第一主成分,U2: 第二主成分...Um: 第m主成分。

2 预测模型描述

2.1 遗传算法

遗传算法是一种模拟自然进化过程中群体遗传机理与自然选择的计算模型。 在遗传算法最开始, 都会随机产生一些初始种群, 然后根据已有的目标函数对这些初始可能解进行评估, 得出适应度值。 基于适应度值挑选“适者”, 将其留下, 即优胜劣汰, 适者生存。 误差较大的可能解被淘汰, 而剩下的经过交叉、变异产生更优种群。 以此类推, 逐代演化最终将产生最优种群, 然后对最优种群进行解码, 得到最优解。

2.2 BP 神经网络

BP 神经网络学习的框架由信号的正向传播与误差的反向传播构成。 在信号正向传播阶段, 通过传入层传入到隐含层, 再经过各隐含层处理传出到输出层, 最终得到实际输出。 当实际输出与期望输出之间的误差太大, 不符合要求, 则进行的反向传播。 在反向传播过程中, 误差首先以某一形式经过隐含层, 在隐含层对其处理之后向输入层传播。 在这一过程中,误差将被平均分给各单元。 每个单元的误差信号将被获取, 并将其作为依据修正权值。 在上述过程周而复始的进行中, 权值在不断调整、 神经网络也不断的学习, 直至神经网络实际输出与期望输出之间的误差符合要求或者学习次数达到了预先设定。 BP 神经网络示意图(图1) 及公式推导如下:

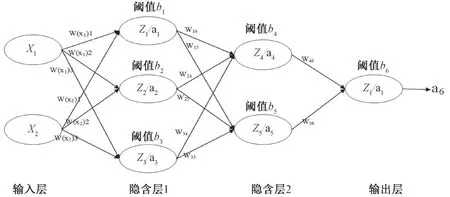
图1 BP 神经网络示意图Fig.1 Schematic diagram of BP neural network

2.2.1 正向传播

①由下式可获取隐藏层1、 2 的输出a1、a2、a3、a4、a5、a6, 以a1和a4为例:

a1= f(Z1)= f(W(x1)1×x1+W(x2)1×x2+b1)(5)

a4= f(Z4)= f(W14× a1+ W24× a2+ W34× a3+b4) (6)

②经过输出层处理得到预测值a1, 公式如下:

a6= f(Z6)= f(W46× a4+ W56× a5+ b6)

2.2.2 反向传播

训练数据对应的目标函数公式为:

其中,Y(i): 期望输出,O(i): 实际输出,n: 输出层节点数。

以上图为例, 进行反向传播公式推导:

2.2.2.1 更新输出层权值(以W46为例)

使用式(8) 对输出层和隐含层2 的权值求偏导:

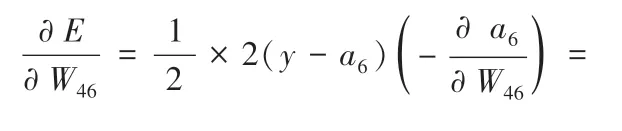
2.2.2.2 更新隐藏层2 的权值

首先, 通过式(9) 理解多元函数链式法则:

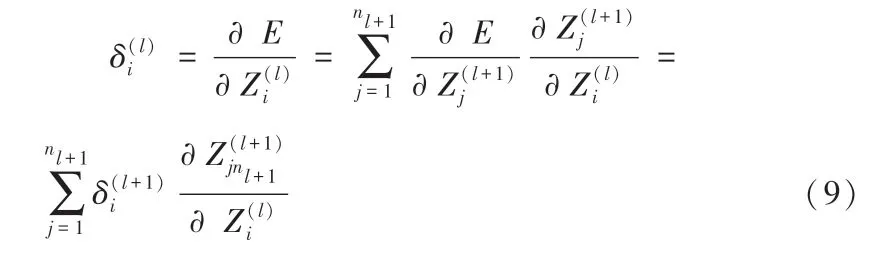
其中:l为层数,nl+1为l+1 层节点数。

然后对隐含层1 和隐含层2 的权值求偏导(以W14为例):

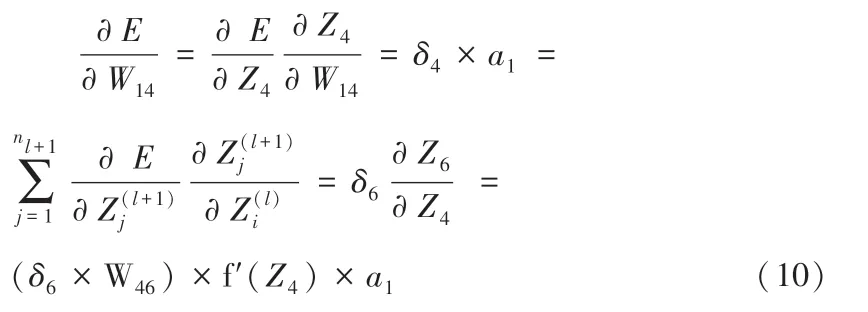
2.2.2.3 更新隐含层1 权值

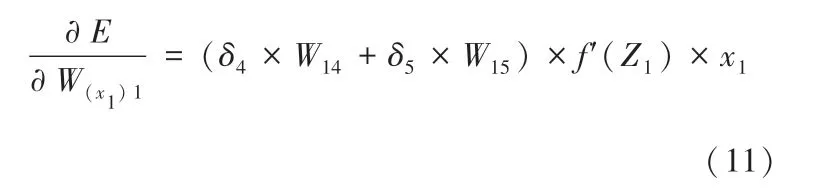
2.2.2.4 更新输出层和隐含层阈值

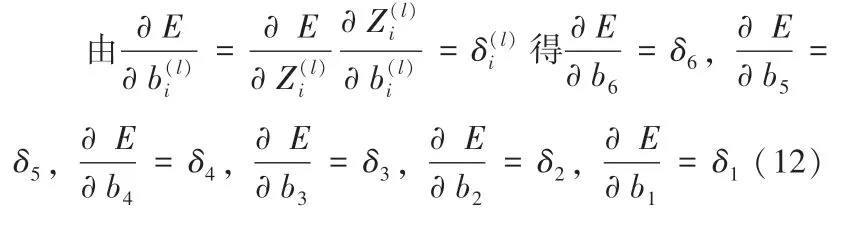
2.3 GA-BP 神经网络

GA-BP 神经网络是在遗传算法与BP 神经网络基础上建立的, 可以将其理解为优化的神经网络, 其优化主要体现在利用GA 的全局寻优能力优化连接权,优化结构, 优化学习规则三个方面[11], 进而实现提高学习速率与运算速率, 达到GA-BP 神经网络的全局优化能力。 具体流程如图2。

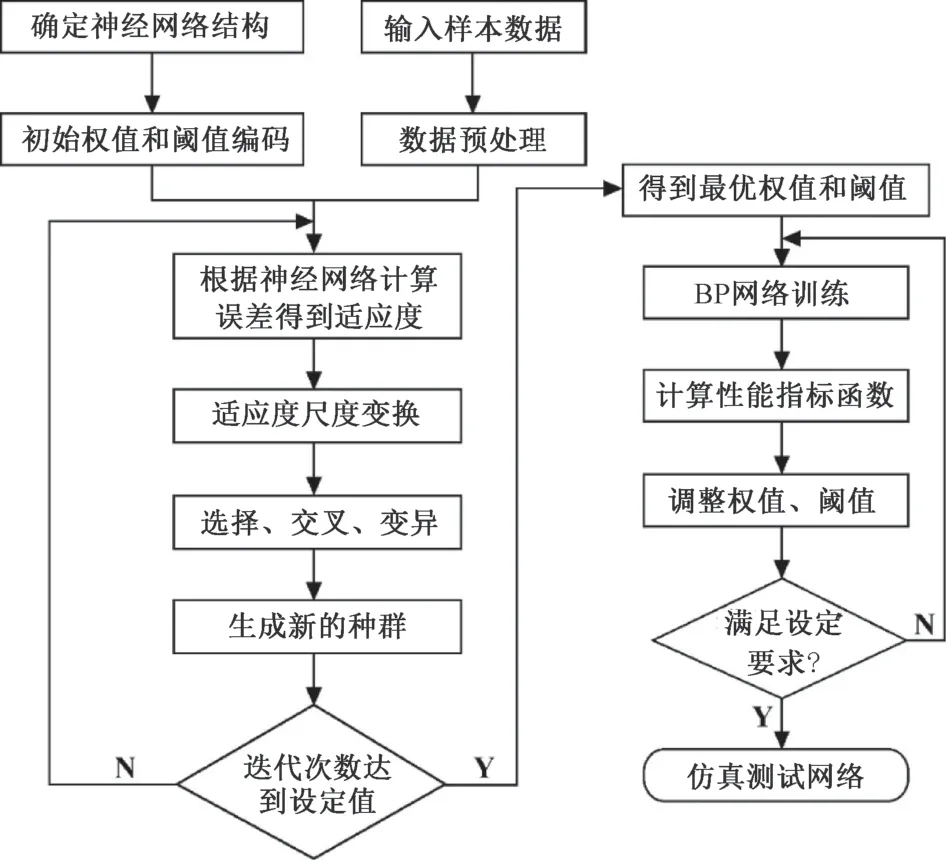
图2 GA-BP 神经网络流程图Fig.2 Flow chart of GA-BP neural network

3 预测模型的建立

3.1 评价指标的确定

评价指标选取是否合理直接影响预测结果的准确性, 地质灾害危险性主要受到地形地貌、 地质环境及特征、 地下水特征、 人类活动等因素影响。 本文选取岩土体结构、 断裂分布密度(km/km2)、 地面坡度(℃)、 地形最大高差(m)、 冲沟发育度、 多年平均降雨量(mm/年)、 植被覆盖率(%)、 人类活动、 地下水特征作为地质灾害危险性评价指标, 并以文献[10] 中的23 组秦岭北麓周至-蓝田段山前地区地质灾害危险性实测数据为例。 为了避免由于中危险区域学习样本太少, 数据集不平衡, 出现误导性错误, 导致模型学习效果不佳。 因此本文通过使用数据扩充公式[12], 将低、 中危险区数据样本分别扩充2 组和5组, 与文献[10] 中23 组实测数据共同构成原始数据集。 上述9 个影响因子与地质灾害危险性之间的关系需要用数值表示, 由于岩土体结构、 冲沟发育程度、地下水特征、 人类活动4 个因子无法用数值精确表示,因此不能直接量化。 所以, 根据相关规范、 文献对上述指标危险性进行分级, 并对其打分量化[13-15], 进而得到影响危险性分级表, 见表1。 其中低危险区由1 分代表、 中危险区由2 分代表、 高危险区由3 分代表。 将30 组原始样本数据归一化处理, 从中挑选训练样本21组, 测试样本9 组, 分别见表2、 表3。

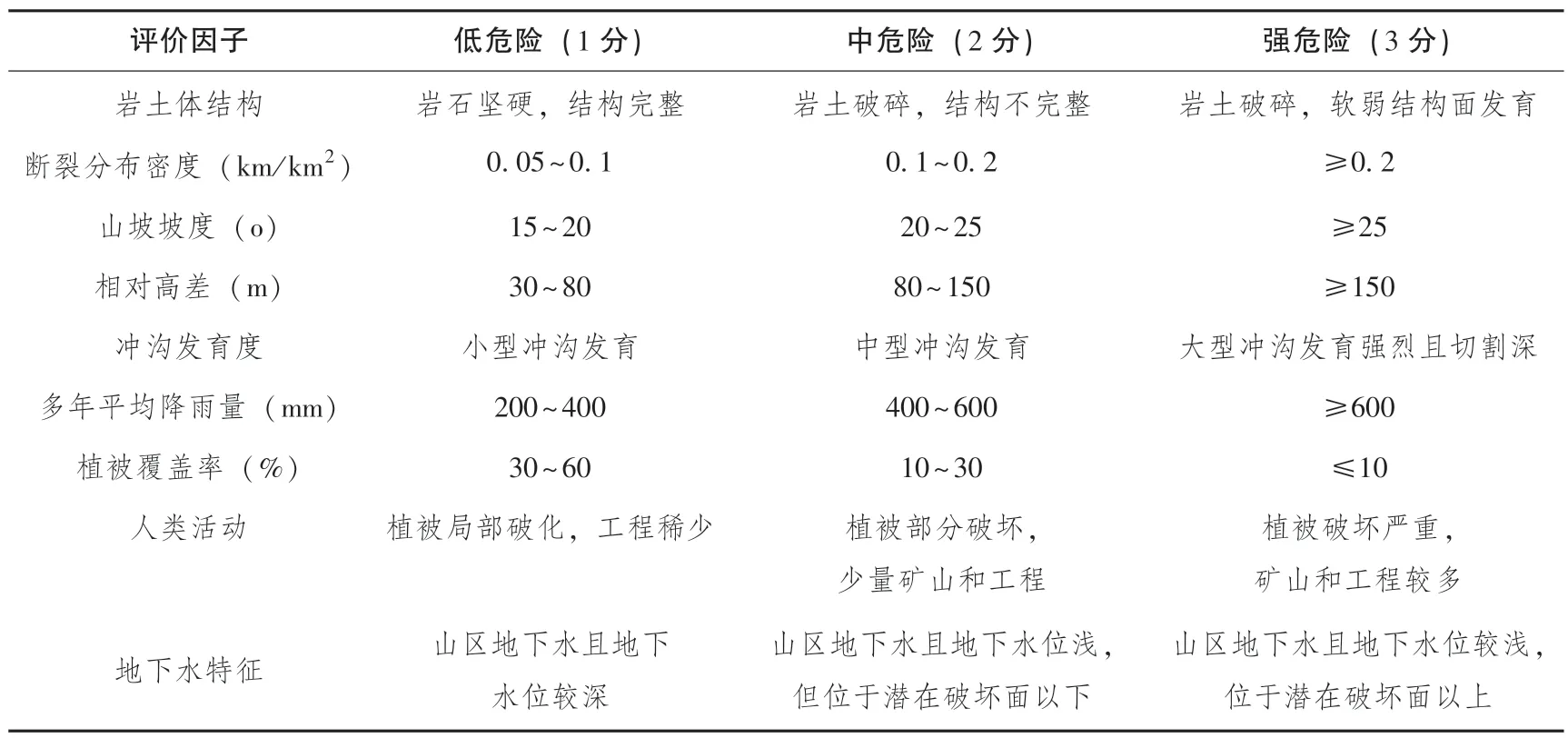
表1 影响因子危险性分级表Table 1 Risk classification of impact factors

3.2 危险性评价指标主成分提取

通过对归一化之后的指标(表2、 表3) 进行分析, 进而得到相关系数矩阵(表4)。

表2 归一化处理后的训练样本Table 2 Training samples after normalization

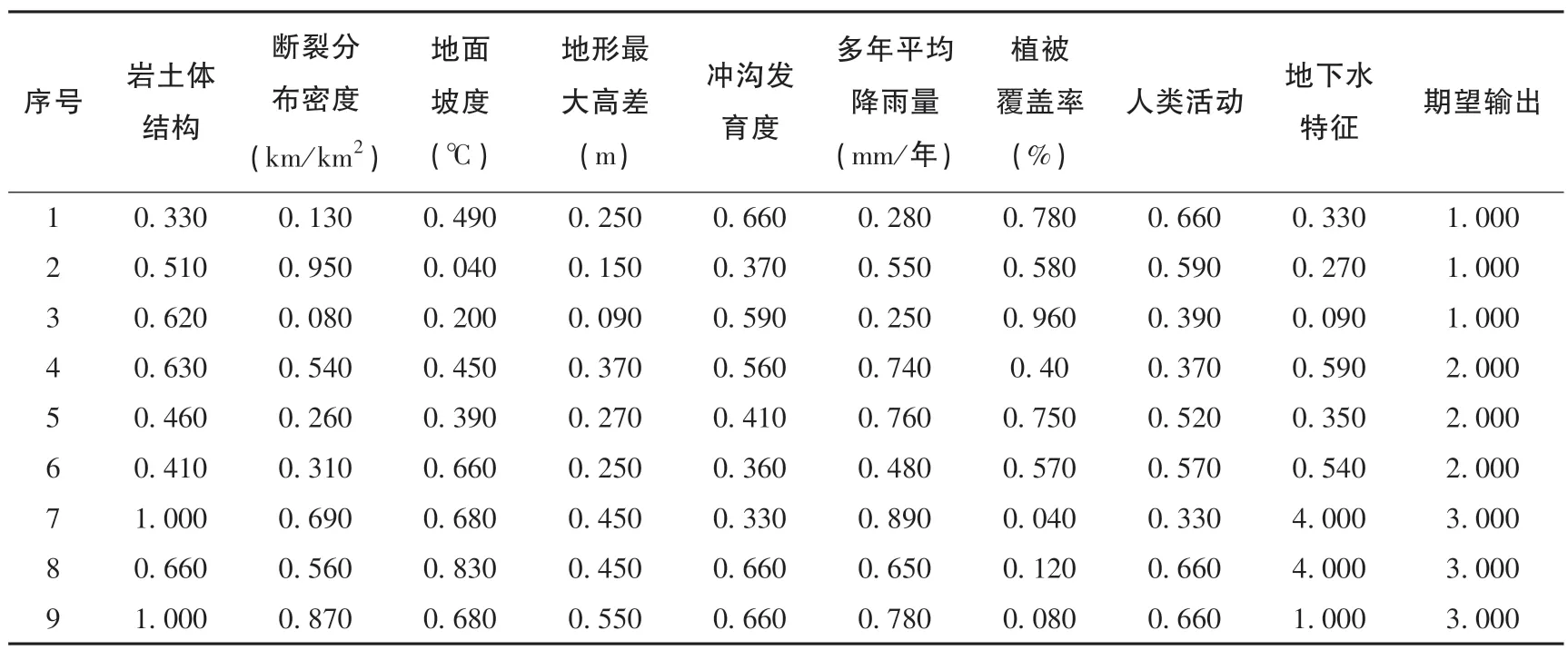
表3 归一化处理后的测试样本Table 3 Test samples after normalization

相关系数越接近1 则说明指标间的相关性越大。由表4 可以看出岩土体结构与植被覆盖率、 地面坡度与地形最大高差、 多年平均降雨量与植被覆盖率等指标间具有很强的相关性, 如果对这些具有较强相关性的因子直接分析, 会导致严重的共线性现象。 主成分分析法可以在保留原始信息的前提下, 重新提取适量线性无关的主成分作为新的指标, 并对其进行线性组合。

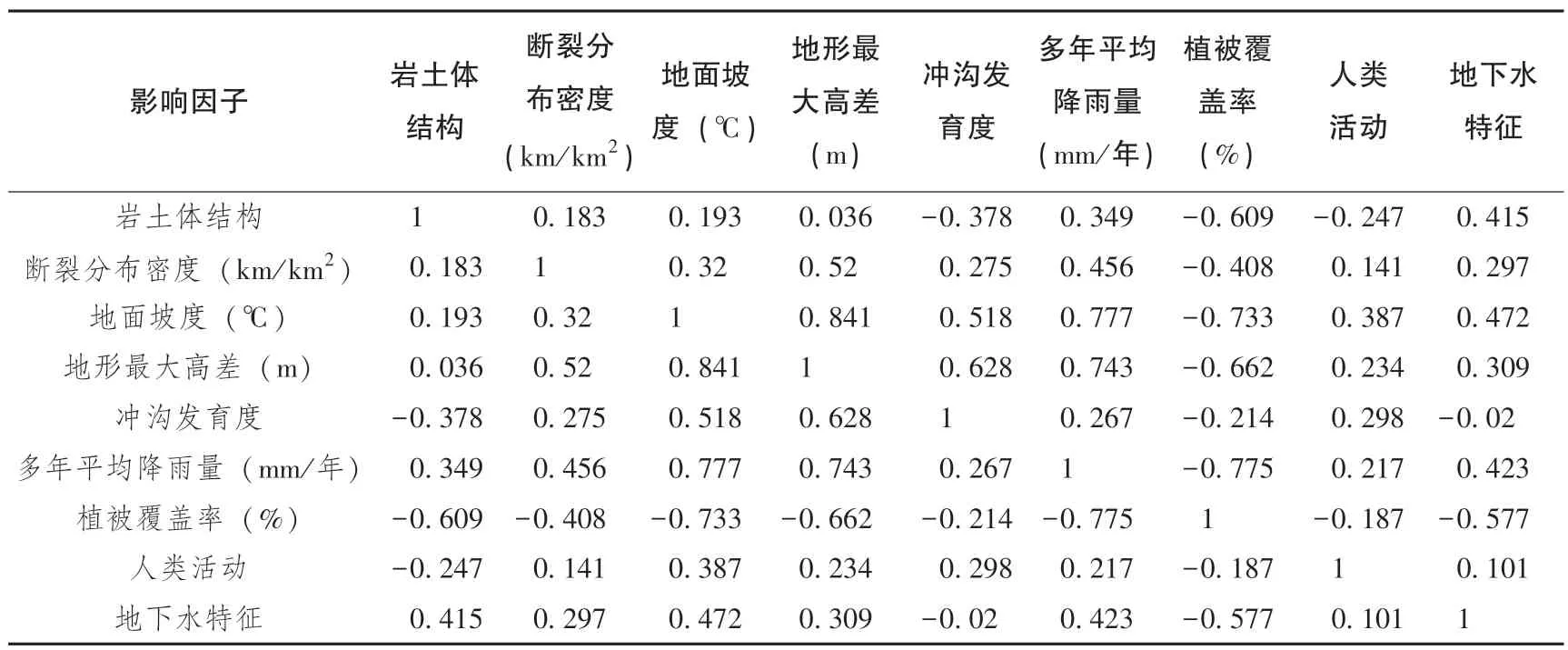
表4 相关系数矩阵Table 4 Correlation coefficient matrix

为了解各主成分对原始指标的信息提取率, 通过对上述评价指标分析, 得到各影响因子的公因子方差比, 见表5。

由表5 可得: 其中断裂分布密度(km/km2)、 地面坡度(℃)、 地形最大高差、 人类活动的提取率都在90%以上, 而信息提取率最低的指标为地下水特征, 达到63.2%, 说明整体指标的信息提取较充分。

表5 公因子方差比Table 5 Common factor variance ratio

通过对上述9 个影响评价指标进一步分析, 得到各主成分特征值及贡献率如表6 所示。

由表6 可得: 第1 主成分的特征值与贡献率分别为4.276、 47.515% ; 第2 主成分的特征值与贡献率分别为1.890、 20.995%; 第3 主成分的特征值与贡献率分别为0. 873、 9.697%; 第4 主成分的特征值与贡献率分别为0.724、 8.044%。 由于前4 个主成分的累计贡献率为86.250%＞85%, 并且结合图3 的碎石图可以看出, 从第5 个主成分以后的特征值相对较低。所以本文提取前4 个主成分就可以代表原始数据的大部分信息。

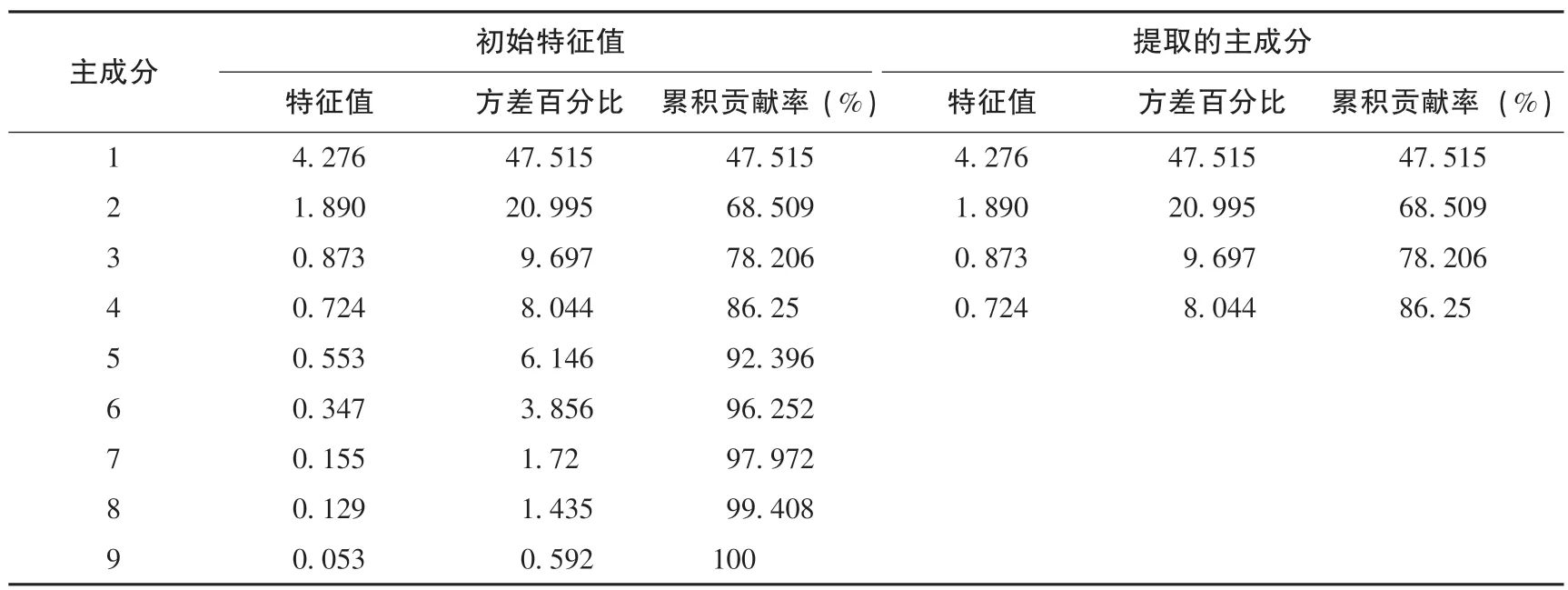
表6 主成分特征值及贡献率Table 6 Principal component eigenvalues and contribution rate

图3 主成分分析碎石图Fig.3 Gravel diagram of principal component analysis

通过最大方差法对因子进行旋转, 得到因子载荷矩阵如表7 所示。

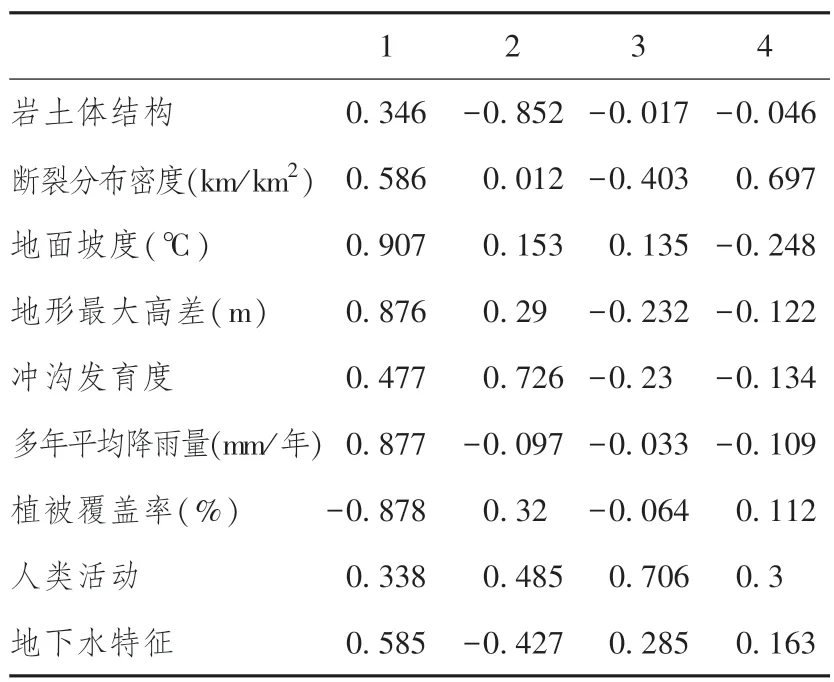
表7 因子载荷矩阵Table 7 Factor load matrix

由表7 可得: 在第1 主成分中, 系数绝对值较大的指标为地面坡度、 地形最大高差、 多年平均降雨量、 植被覆盖率, 表明第1 主成分主要代表这4 个指标, 所以地形地貌与降雨对地质灾害的影响。 同理,岩土体结构与冲沟发育情况对地质灾害的影响主要由第2 主成分反映; 人类活动对地质灾害的影响主要由第3 主成分反映; 研究区断裂带分布情况对地质灾害的影响主要由第4 主成分反映。

通过将表7 因子载荷矩阵中各元素除以相应特征值的平方根, 进而得到指标得分系数矩阵, 如表8所示。

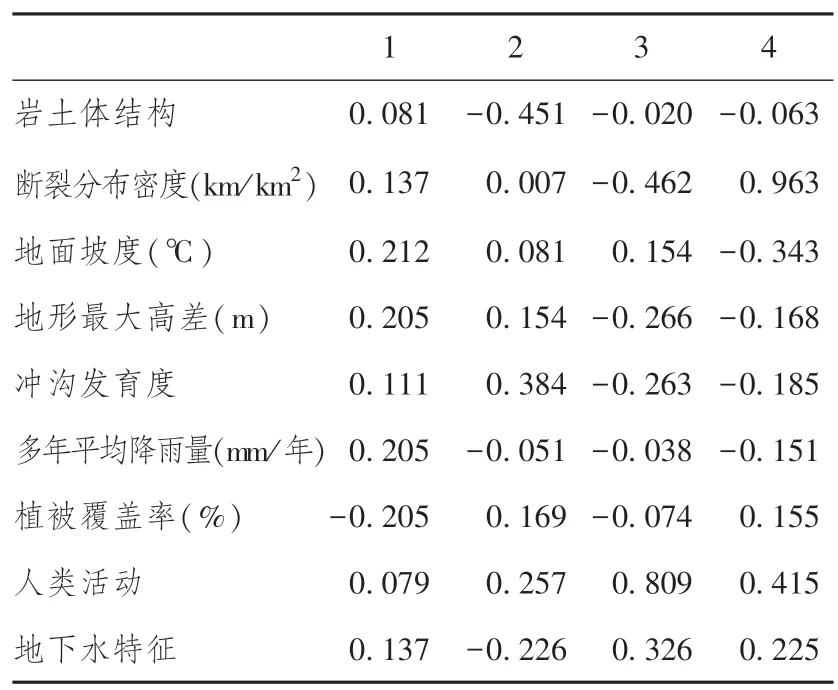
表8 指标得分系数矩阵Table 8 Index score coefficient matrix

原始9 个研究指标可以通过该系数矩阵重新进行线性组合, 进而得到新的、 线性无关的4 个主成分Y1、Y2、Y3、Y4, 即 第1、 2、 3、 4 主 成 分, 见 式(13)。 其中x1代表岩土体结构、x2代表断裂分布密度(km/km2)、x3代表地面坡度(℃)、x4代表地形最大高差(m)、x5代表冲沟发育度、x6代表多年平均降雨量(mm/年)、x7代表植被覆盖率(%)、x8代表人类活动、x9代表地下水特征。

上述样本数据经主成分分析提取, 用4 个线性无关的主成分代替之前的9 个指标, 使得冗余的数据被精简, 由不同量纲带来的负面影响得以消除, 研究指标之间的相关性及其维数被降低, 可以提高后续GABP 神经网络预测模型的运算效率。

3.3 GA-BP 神经网络模型的建立

根据前人研究, 3 层BP 神将网络可以逼近任意非线性函数[16]。 本文根据3 层BP 神经网络建立如下预测模型:

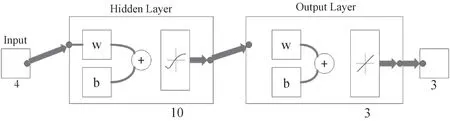
图4 神经网络结构层次Fig.4 Hierarchy of neural network structure

本文在使用GA 算法优化BP 神经网络时, GA 的最佳求解参数设置为: 迭代次数50, 种群规模10, 交叉概率选择0.2, 变异概率选择0.1。 BP 神经网络参数设置为: 训练次数1000, 学习速率0.01, 训练目标最小误差0.000 01, 显示频率25, 动量因子0.01, 最小性能梯度1e-6, 最高失败次数6。 通过对上述参数的设置, 运行程序反复寻找最优w、 b, 最终得到最优预测结果。

3.4 预测结果对比与分析

为检验PCA-GA-BP 神经网络模型对地质灾害危险性的预测效果及其稳定性, 本文将其与当前流行的PCA-PSO-BP、 RS-GA-BP 预测模型分别训练10 次,再取三类预测模型的最优预测结果与平均预测结果分别进行对比分析。

3.4.1 最优预测结果对比分析

为增加三类预测模型对地质灾害危险性预测结果的可视化程度的同时在微观上把握其内在分类。 本文取上述三类预测模型训练集最优学习结果、 预测集最优预测结果的混淆矩阵图, 即图5、 图6、 图7 进行对比分析。

由上述模型的训练集混淆矩阵图, 即图5 (a)、图6 (a)、 图7 (a) 可得: PCA-GA-BP、 PCA-PSOBP 预测模型对所有危险区的训练结果都是100%。RS-GA-BP 预测模型对第一类与第二类危险区的训练结果为100%, 第三类危险区的训练结果为85.7%, 7个训练集中, 正确学习的有6 个, 剩下的1 个被错误的归为第二类。

由上述模型的测试集混淆矩阵图, 即图5 (b)、图6 (b)、 图7 (b) 可得: PCA-GA-BP 和RS-GA-BP预测模型的最优结果中对三类危险区的预测全部正确。 PCA-PSO-BP 预测模型第一类危险区的3 个测试集里有2 个预测正确, 剩下1 个被误判为第二类, 第二类和第三类危险区预测正确率皆为100%。

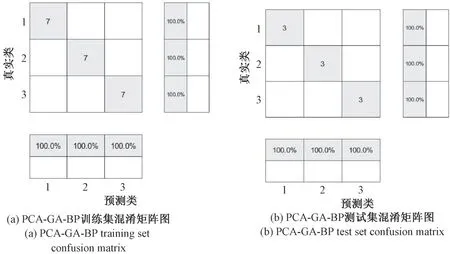
图5

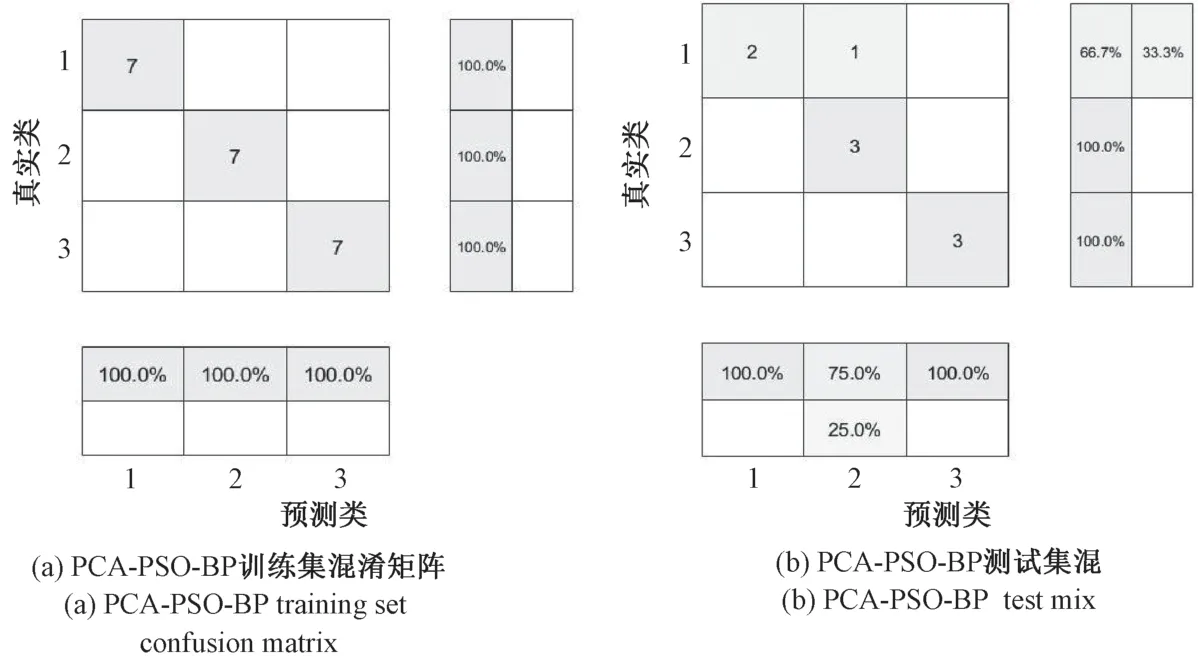
图6

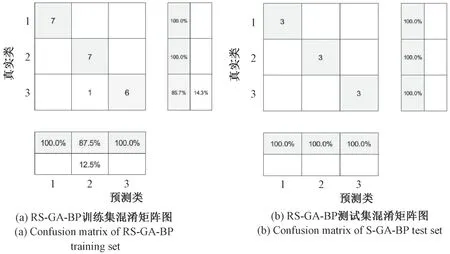
图7

综上所述, PCA-GA-BP 预测模型的训练结果与预测结果在最优情况下的准确率都是100%, 结果比较理想。 而PCA-PSO-BP 与RS-GA-BP 预测模型分别在训练过程或预测结果中都有错误的情况。 由此得出:PCA-GA-BP 预测模型在最优情况下的学习效果和预测能力都较强。

3.4.2 平均预测结果对比分析

为了解各模型的稳定性以及随机赋权重对模型预测结果的影响, 取上述每种模型运行10 次的测试样本平均结果进行对比, 见表9。

通过PCA-GA-BP、 PCA-PSO-BP、 RS-GA-BP 预测模型10 次训练的平均正确率分析可知: PCA-GA-BP、PCA-PSO-BP、 RS-GA-BP 三类模型平均正确率分别为87.778%、 78.889%、 70.000%。 PCA-GA-BP 平均正确率＞PCA-PSO-BP 平均正确率; PCA-GA-BP 平均正确率＞RS-GA-BP 平均正确率。 说明GA 算法对BP 神经网络中w 和b 的优化能力要优于PSO。 PCA 对指标处理能力要优于RS。 由此可得, PCA-GA-BP 预测模型对地质灾害危险性预测的正确率要高于表9 中的其它预测模型。 PCA-GA-BP、 PCA-PSO-BP、 RS-GA-BP三类预测模型最优预测结果的正确率100.000%、88.889%、 100.000%, 与其相应的平均预测结果整体正确率分别相差12.222%、 10.000%、 30.000%。 由此可得: PCA-GA-BP 和PCA-PSO-BP 预测模型都比较稳定, 而RS-GA-BP 预测模型可能受指标与随机赋权重的影响导致预测模型稳定性相对较低。

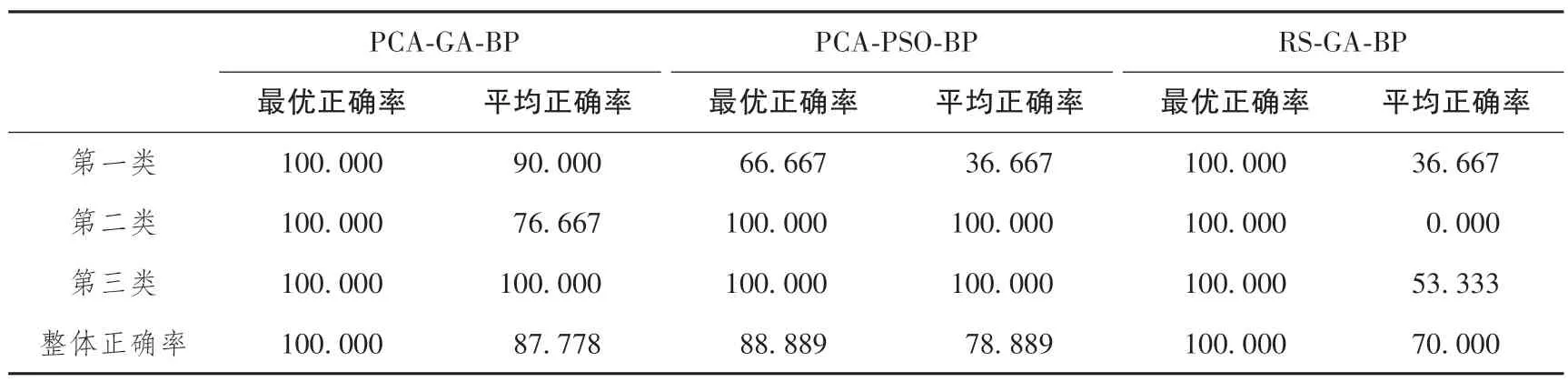
表9 正确率对比表(%)Table 9 Comparison of accuracy (%)

因此, 在真实危险性未知的实际地质灾害危险性预测工程中为了保证预测结果准确性, 应该选择相对稳定并且正确率较高的模型, 所以在上述模型中应该优先选择PCA-GA-BP 危险性预测模型。

4 结论

(1) 对于维数较多的样本数据, 使用主成分提取的方法可以在保留原始数据大部分信息的基础上降低维数和主成分之间的相关性, 提升运算效率。

(2) 利用GA 所具有的寻优能力和全局搜索能力, 能够优化模型的权值、 阈值。 可以有效避免BP神经网络局部极小的缺陷, 同时节约了训练时间, 更好地确保了预测模型的精度与有效性。

(3) 在实际地质灾害危险性预测工程中, 由于预测结果的未知性, 因此在地质灾害危险性预测模型的选择时, 应该在高准确率的基础上选择更稳定的模型。 可以在有限样本的基础上, 建立影响因子与危险性之间的非线性映射关系。 为预测和研究分析地质灾害危险性提供了新思路, 具有广阔的应用前景。