桉树人工林单木地上生物量空间效应分析

罗大鹏 农明川 李会朋 王俊峰 欧光龙

（1. 西南林业大学林学院，云南 昆明 650233；2. 西南林业大学西南地区生物多样性保育国家林业局重点实验室，云南 昆明 650233）

森林生态系统作为地球上维系生态平衡和物质循环的主要生态系统，在全球大气循环研究中居重要地位[1]。森林生物量约占陆地生态系统植被总生物量的90%，在维持全球气候稳定、调节全球碳平衡、减缓大气温室气体浓度上升等方面具有不可替代的作用[2]。对森林生物量的研究关系到生态系统生产力、碳循环，是全球变化研究的基础参数，同时森林生物量也是表征植物活动的关键变量[3]。森林生物量普遍存在空间效应，忽视森林生物量的空间效应可能会带来生物量变化分析的有偏估计或者误差[4-5]。

空间效应分析可以用于检验森林生物量在空间上的相关性强弱以及在空间上的变异性[6]，主要表现为空间异质性和空间自相关性两个方面[7-8]。空间异质性普遍存在于自然界中[9]，它是指系统或系统属性在空间分布中的复杂性和变异性，系统属性可以是生物量，土壤含氮量等生态学变量[10]；空间异质性在一定程度上反映森林生物量在空间上的差异，且空间异质性的评价方法随空间数据类型的不同而存在差异，空间异质性的研究理论常用的有地统计学方法，也有研究使用组内方差对空间异质性进行分析[11-12]。空间自相关是一种表现地理数据在空间上的依赖程度的统计方法[13-14]，研究对象集聚或离散效果最显著时的距离阈值，分析变量间的空间自相关，可以大幅度提升空间格局分析的精度[15]。反映整个研究区域内总体的全局空间自相关指数，以及描述区域内研究对象与其相邻单元间的空间相关性的局域空间自相关指数（LISA）是分析描述空间自相关的两个重要方面[16-20]。关于森林生物量的空间效应分析，农明川等[5]对昆明市云南松（Pinus yunnanensis）生物量的空间分布规律进行研究，指出昆明市云南松地上生物量呈现显著的空间自相关关系；张维生[17]以空间自相关分析方法为基础，对黑龙江省的森林和地貌等因子进行了研究，指出该地区的森林、地貌等因子的存在空间正相关性；王维芳等[18]也基于相似的方法对帽儿山地区的森林生物量的空间自相关性进行了分析，同样得出了相似的结论。但是这些分析在一定程度上揭示在区域尺度上森林生物量的空间分布模式，以及森林生物量分布的空间自相关性；尤其是在林分尺度上，揭示林内单木生物量间的空间效应变化规律的研究较少，欧光龙等[20]采用空间回归模型构建思茅松（Pinus kesiya）不同维度的单木生物量模型，取得了较好的拟合效果，这在一定程度上说明了各维度单木生物量是存在空间效应的，但是没有对空间及邻近木关系进行研究；徐美玲等[21-22]对云南省思茅松林的混交度、大小比数和角尺度几个空间结构参数进行量化分析，结果表明思茅松天然林整体呈现均匀分布。这些研究表明林木单木各维度生物量存在空间效应，但是基于实测数据，准确描述林内林木各维度间的空间效应关系的研究仍然缺乏。

桉树（Eucalyptusspp.）由于适应环境能力强、生长迅速，经营周期短，单位面积产量高等特点，成为了热带和亚热带地区最重要的人工林树种[23]，也被认为是世界人工造林三大速生树种之一，是中国南部省区极其重要的速生丰产林造林树种。分析桉树人工林单木生物量各维度间的空间效应，揭示其生物量空间变化规律对于准确描述林木生物量生长变化规律至关重要。基于此，本研究以云南省楚雄州桉树人工林皆伐样地（100 m×30 m）的单木各维度生物量（木材、树皮、树干、树枝、枝叶、树冠以及地上生物量）的实测数据为基础，采用空间自相关和空间异质性分析方法，对楚雄州东华镇桉树人工林地上生物量的空间分布规律进行研究[24]，以获知桉树人工林各维度生物量的空间分布差异。在此基础上深入分析各维度生物量空间分布差异的成因，并确定桉树人工林单木各维度生物量空间效应研究的最佳距离阈值，从而准确获取区域森林生物量的空间分布信息，以期为提高桉树人工林的经济效益和生态效益提供理论依据。

1 材料与方法

1.1 研究区概况

东华镇位于云贵高原中部的云南省楚雄州西南部，地处东经101°21′29″～101°31′34″，北纬24°26′36″～25°01′16″，总面积448 km2，由于地处紫溪山南麓，整体地势呈东北低、西南高的特点。平均海拔1 895～1 990 m，属于亚热带季风气候，其年均温、年均降雨量、年均日照、平均降霜期分别为15.6 ℃、831 mm、2 422 h、96 d，楚雄州境内分布植被类型主要为中亚热带常绿阔叶林和针叶林[25]。

1.2 样地调查

图 1 样地示意图Fig. 1 The map of study plots

本研究所用数据为2019年12月于楚雄州实测调查，单木生物量的测定参考《林木生物量模型研究》[26]。树枝生物量和树叶生物量的测定采用全称重法，即先测出树枝和树叶质量，然后分别取样烘干后求出含水率进而推算出树枝和树叶的质量。对于胸径较小的树干采用全称重法测定生物量，而胸径较大的树干生物量则采用材积密度法测定，即通过对树干进行取样，测定样品的质量和体积（样品体积通过排水法测定）从而求算其密度，进而推算树干生物量[27]，样木生物量信息见表1。

表 1 样木基本信息Table 1 The basic characters of sample trees kg

1.3 样地边缘校正方法

本研究采用的样地边缘校正方法为：Simulate Outer Boundary Values。此方法会在研究区域边界外，创建边界内所发现点的镜像点，以便校正边界附近的低估现象。将镜像与研究区域的边的最大距离范围相等的距离内的点，使用镜像的点会使边界点的相邻点估计更加精确[28]。

1.4 空间分布模式

本研究选择Ripley'sK函数来描述单木地上生物量的空间分布模式，K函数作为一种基于距离的概括要素空间分布累积特征的方法，常被用来描述点要素在空间范围内的相关性程度，反映要素随尺度变化而呈现出的空间分布模式[29]，为了克服K函数的方差不稳定的问题，Besag[30]将K函数进行开方线性转化为L函数，转化后的L函数公式如下：

式中：A是研究区面积；d表示距离阈值；n为点要素数量；k(i,j)为权重，距离d的最大值取值应为最短边的一半，大于该距离可能导致分析结果不准确；通过比较真实点的L(d)和样地空间随机点（CSR）之间的d，若L(d)>0则表明在尺度为d时研究对象为聚集分布；L(d)<0则说明研究对象呈离散分布；而L(d)=0则表明研究对象呈随机分布。

1.5 空间自相关分析

1.5.1全局Moran'sI

全局Moran'sI是全局空间自相关分析的重要指标，它能反映出研究区域内的对象的总体空间聚类模式[31]。

式中：I是全局Moran's指数值；n是变量x的观测数；xi、xj分别为位置i和位置j的生物量值；是所有生物量的平均值；wij是空间权重矩阵值。

“增值税和营业税两税并存，导致增值税抵扣链条中断，不利于生产性服务业的发展”。例如，有三家企业ABC，A企业从事生产性服务，如果A企业不从生产企业B中独立出来，那么在为B企业提供业务服务的过程中就可以不需要征收营业费用，而从其他企业购进资源也可以从B企业的增值税中进行抵扣，但是一旦A企业从B企业中独立出来，就会出现A企业再为B企业提供服务就要缴纳营业税，从其他企业购进为B企业服务所需要的资源的增值税也不能再从B企业中抵扣，这就导致企业重复征税，负担增大，不利于企业的生产、服务相分离。但是如果生产性服务业不从母体中独立出来，难以实现自身的发展。当前的税收制度不利于将制造业和服务业进行融合发展。

全局Moran's指数I的取值意义随Z(I)的阈值的不同而存在差异。

式中：Z(I)是空间聚类模式强度的衡量指标；E(I)和Var(I)分别是指数值I的期望值和方差；在给定的置信水平下（假定α=0.1），若I<0，Z(I)<-1.96表示空间要素间存在显著的空间负相关性。若I<0，Z(I)<-2.58表示空间要素间存在极显著的空间负相关性，表现为相异聚集（也称异常值），即相邻要素的属性值间差异较大的聚集在一起；若I>0，Z(I)>1.96表示观测对象间存在显著的空间正相关关系。若I>0，Z(I)>2.58表示观测对象间存在极显著的空间正相关关系，呈现出相似聚集的现象，即相邻要素属性值间差异较小的相互聚集；若I=0或-1.96≤Z(I)≤1.96则表示观测对象间不存在空间相关性，随机分布于研究区域内[32]。

1.5.2局部Moran's指数

局部Moran's指数可用于反映局部区域内特定属性值间是否存在空间自相关关系。在本研究中，它是一种弥补全局Moran's指数仅能对总体的空间自相关情况进行分析而不能反映特定地点研究对象与其相邻要素间的空间相关性的缺陷的方法[33]。局部Moran's指数（Ii）的计算公式如下所示：

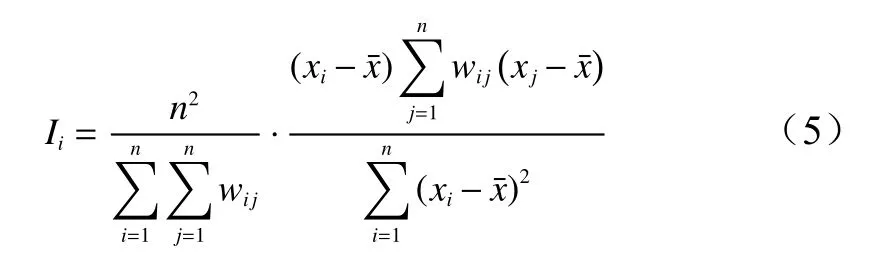
式中：Ii是局部Moran's指数值；n是变量x的观测数；xi、xj分别为位置i和位置j的属性值；是所有属性值的均值；wij是空间权重矩阵值。

1.6 空间异质性分析

空间要素的空间异质性可以通过组内方差进行描述，组内方差可定量地描述研究对象的局部空间异质性，是分组距离大小的函数，通常会随着分组距离的增加而增大[34]，其表达式如下：

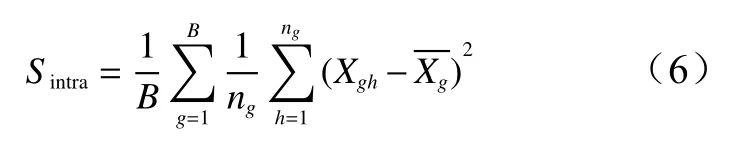
式中：B是特定分组距离下的组的数量，g为特定分组，ng为特定组内样本量，Xgh是在第g个组中的第h个生物量值，是在第g个组内的生物量X的平均值。

1.7 数据处理

使用Excel 2019软件对实测数据进行标准化处理和相关表格的制作，使用ArcGIS 10.6软件下的多距离空间聚类分析工具进行空间分布模式的分析，增量空间自相关工具进行全局空间自相关分析，聚类与异常值分析工具进行局部空间自相关分析，空间异质性的组内方差分析在SPSS 20.0中完成。

2 结果与分析

2.1 桉树生物量空间分布模式分析

从单木各维度生物量的Ripley'sK函数经变换后的L函数的变化曲线可以看出，除树叶生物量（图2e）外，桉树人工林各维度生物量空间聚集模式呈现相似的规律，均以2 m为界，2 m以内均呈现离散分布，2～14 m左右呈现聚集分布，15 m以后均呈现离散分布（图2）。其中木材生物量空间分布格局在0～2 m范围内离散分布，2～14 m范围内表现为聚集分布，14～25 m范围内表现为离散分布（图2a）；树皮生物量在0～2 m范围内离散分布，2～15 m范围内表现为聚集分布，15～25 m范围内表现为离散分布（图2b）；树干生物量空间分布格局在0～2 m范围内离散分布，2～14.5 m范围内表现为聚集分布，14.5～25 m范围内表现为离散分布（图2c）；树枝生物量空间分布格局在0～2 m范围内离散分布，2～14.5 m范围内表现为聚集分布，14.5～25 m范围内表现为离散分布（图2d）；树叶生物量在0～1 m之间呈现聚集分布，1～3.5 m为离散分布状态，3.5～25 m呈现聚集分布趋势，且在18.5～21.5 m范围内呈现显著聚集分布（图2e）；树冠生物量空间分布格局在0～2 m范围内离散分布，2～14.5 m范围内表现为轻度聚集分布，14.5～25 m范围内表现为离散分布（图2f）；树枝生物量空间分布格局在0～2 m范围内离散分布，2～13.5 m范围内表现为轻度聚集分布，13.5～25 m范围内表现为离散分布（图2g）。总体来看，桉树人工林全林各维度生物量观测值均介于上下包迹线之间，且各维度生物量实际值更接近于上包迹线，聚集特性不是很明显。

图 2 桉树人工林各器官维度生物量L函数变化图Fig. 2 L-function changes in different component biomass of Eucalyptus plantation

2.2 桉树生物量全局空间自相关分析

桉树人工林全林的各维度生物量的增量空间自相关分析结果见图3。由图3可知，桉树人工林树枝生物量7 m、树叶生物量5.5 m和7 m、树冠生物量5.5 m和24～25.5 m时呈负的空间自相关，此时生物量呈现高值与低值相聚集的聚类模式。其他距离上均呈正空间自相关，生物量存在高值于高值或低值于低值聚集的聚类模式。木材、树皮、树干及地上生物量在5～30 m均呈正空间自相关，此时各维度生物量存在高值于高值或低值于低值聚集的聚类模式。

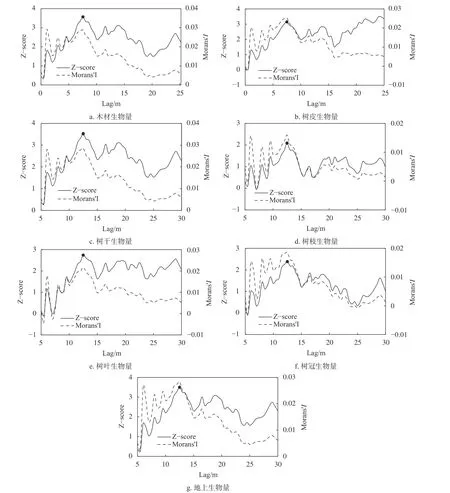
图 3 桉树人工林其他树种各器官维度生物量全局莫兰指数变化曲线Fig. 3 Curves of global Moran's index of different component biomass in Eucalyptus plantation

观测到各维度生物量的Z值达到显著后的第一个聚集峰值所对应的距离均为12.5 m，也就是说当空间距离为12.5 m时空间相关性达到极限，因此，楚雄州桉树人工林的最佳分析距离尺度为12.5 m。随着距离尺度的增加，桉树人工林全林的木材、树皮、树干、树枝、树叶、树冠和地上生物量均表现出一定程度的空间自相关性且空间变化规律相似，但相关性不显著，Moran'sI值范围0.016 0～0.028 9，单木各维度生物量间相关性较低。

2.3 桉树生物量局部空间自相关分析

由图4可知，对于桉树全林各维度生物量而言，均表现出了不同程度的空间自相关关系，且各维度生物量的空间自相关变化特征相仿。在样地左侧基本呈现出明显的高值于低值聚集（HL）并伴有低值于低值聚集（LL）的情况；在样地右侧基本呈现出明显的低值于高值聚集（LH），在样地右侧还出现明显的高值于高值聚集（HH）并伴有低值于高值聚集（LH）；由表2可知，从桉树人工林全林来看，尽管85%的生物量值没有呈现出显著的自相关性（NS），但是15%的生物量值显示出显著的空间自相关，其中4%的生物量值显示出极显著的空间自相关，说明各维度生物量在局部区域内存在显著聚集现象。

图 4 桉树人工林各维度生物量局部Moran's 指数空间分布Fig. 4 Spatial distribution of local Moran's index of different component biomass in Eucalyptus plantation

表 2 桉树人工林单木各维度生物量聚类模式统计Table 2 Statistics of biomass clustering model of Eucalyptus plantation in each dimension

2.4 桉树生物量空间异质性分析

由图5可知，以5 m为界限，在5 m以内随着距离的增加各维度生物量的空间变异性增加较为迅速，5 m以后增速较为平缓，但是一直保持缓慢增加的趋势。从维度来看，树叶生物量的空间变异程度明显大于其他维度的生物量。在0～30 m的小尺度范围内，桉树林人工林各维度生物量的空间变异较小，这说明桉树人工林各维度生物量随着距离尺度的增加，桉树人工林的空间变异逐渐增大，且在距离5 m后空间异质性变化趋于稳定。

图 5 桉树人工林各维度生物量组内方差Fig. 5 Intra-block variance of different component biomass in Eucalyptus plantation

3 结论与讨论

已有学者就大尺度单一树种的森林生物量空间效应进行研究，但几乎没有研究基于实测数据描述单木水平维度生物量的变化特征[35-36]。本研究基于楚雄州0.3 hm2桉树人工林皆伐实测样地，分析了桉树人工林木材、树皮、树干、树枝、树叶、树冠和地上生物量7个维度生物量的空间分布规律。从空间分布模式看，桉树人工林全林各维度生物量聚集特性均不是很明显。这主要是由于桉树人工林林木分布相对均匀，样地距离尺度较小导致无大规模生物量聚集[37-40]。

从全局空间自相关分析结果来看，全林各维度生物量Morans'I值介于0.016 0～0.028 9，说明桉树各维度生物量均存在一定的空间自相关，桉树生长特性会影响其各维度生物量的空间变化，桉树人工林7～8 a即为成熟林，说明这一速生树种在成熟林阶段，林木已经出现了竞争和林木分化，这在一定程度上造成了林木生物量变化的空间自相关。Zhang等[41-42]采用地理加权回归（GWR）方法来探讨桉树人工林胸径和树高关系，指出桉树人工林的空间分布存在一定的空间自相关，表明桉树人工林单木地上部分各维度生物量和胸径变量在空间自相关变化特征是一致的。

局部空间自相关结果表明，近15%样木在样地内呈现聚集分布，说明桉树人工林生物量存在局部聚集现象。生物量高值主要集中在样地右侧，生物量低值集中在样地左侧及中部，由于样地中部林木较为稀疏，固全林地上部分生物量值由高到低依次为样地右侧、样地左侧、样地中部，且各维度生物量空间分布差异不大。此外，桉树人工林单木生物量的空间分布还受到立地条件等因素的影响，调查样地右侧立地条件较好，林木长势也较好；样地中部土壤较为板结，且林木较为稀疏，长势相对较差。这也造成了立地条件好的右侧生物量高值聚集，立地条件较差的左侧和中部生物量低值聚集，这样的立地条件分布与单木地上生物量值分布一致。这在一定程度上也说明了要准确描述桉树人工林生物量变化规律，空间效应的分析是不可忽略的[43]。

桉树人工林各维度生物量空间变异性均随距离的增加而增大，均在距离5 m后逐渐平稳，且树叶生物量的空间变异程度最大。在给定的距离尺度下树叶生物量较其它维度生物量的空间变异性更大，这是由于树叶作为桉树光合作用固定能量的主要来源，相较于其他器官竞争更为明显，从而导致树叶生物量在空间上的变异程度更大，这也说明了林木各维度生物量在空间效应特征上存在差异。胥辉[27]同时用材积密度法和称重法对吉林省红石林业局的8个树种60株立木树干生物量进行测定，同时，考虑到树干不同位置的密度存在差异可能带来的生物量测定误差，本研究在使用材积密度法测定树干生物量时，以2 m为一个区分段分别对树干不同高度处的密度进行测定，从而提高树干生物量测定精度。

本研究对桉树这一人工引进树种的单木地上各维度生物量空间效应的描述，可为今后其他森林类型的单木生物量空间效应变化分析提供理论支撑，还可将其应用于优化和调节森林结构以充分发挥森林的多种功能，为精准分析林业数据以及林业生产经营实践提供参考和科学依据。由于研究条件有限，本研究样地面积较小，树种单一，也没有对树根这一维度生物量进行研究，且对影响各维度生物量空间分布规律的成因和影响机制探讨深度有限，这些都是本研究的不足之处。今后可在条件允许的情况下扩大调查样地面积，获取更多的样本和数据，对林木生物量空间分布格局的形成机制开展更加深入的探讨，进一步研究更多树种的空间效应[37]。