基于高斯过程回归模型的发动机性能预测
闫雪华 李岩 杨淑玲





摘 要:基于1.5L汽油增压发动机的VVT标定试验,对进排气VVT角度采用拉丁超立方抽样建立试验样本,并构建高斯过程回归模型,通过试验数据分别训练扭矩回归模型和油耗回归模型,使用训练后的回归模型预测发动机扭矩、比油耗。通过与发动机万有特性测试数据对比,结果表明:在发动机扭矩大于25N.m的区域,油耗回归模型的预测值偏差小于5%;在发动机小负荷区域,因测量误差、发动机燃烧等因素影响,油耗回归模型的预测值偏差较高。总而言之,高斯过程回归模型对发动机万有特性的预测具有较高的精度及普适性,为发动机参数的优化工作提供参考。
关键词:高斯过程回归; 发动机性能;发动机标定
中图分类号:U464.171 文献标识码:A 文章编号:1005-2550(2022)02-0061-05
Engine Performance Prediction Base on Gaussian Process
Regression Model
YAN Xue-hua, LI Yan, YANG Shu-ling
( SAIC GM Wuling Automobile Co.,Ltd., Liuzhou 545007, China )
Abstract: Based on VVT calibration test result of 1.5L gasoline turbocharged engine, test plan for VVT Angle of intake and exhaust was sampled via Latin hyper-cube method , torque and fuel consumption Gaussian process regression(GPR) models were constructed. Torque regression model and fuel consumption regression model were trained respectively by test data. Compared the engine universal characteristics with test data, the results show that the deviation of the predicted value of the fuel consumption regression model is less than 5% in the region where the engine torque is greater than 25N.m. Due to the influence of measurement error, engine combustion etc., the predicted value of fuel consumption regression model has high deviation in small engine load area. In a word, Gaussian process regression model has high accuracy and generalization for the prediction of engine universal characteristics, which can provide reference for the optimization of engine parameters.
Key Words:Gaussian Process Regression(GPR); Engine Performance; Engine Calibration 1 前言
随着发动机新技术的使用和电控系统技术的不断发展进步,因新技术引入的相关执行机构增加了电控系统的复杂性,发动机需要标定优化的参数不断增加,不同参数之间的关系也愈加复杂,标定优化的工作量呈指数级增加, 台架实验成本及人工成本也不断激增[1]。为减少标定优化的工作量和提高参数标定优化的精度,实验设计统计方法[2-3]和基于模型标定方法[4-5]被结合起来应用于发动机优化标定。通过引入试验设计方法(DOE),利用部分具有代表性的工况点实验数据构建发动机输入参数和输出响应的数学模型,从而估计出全局工况点下的性能参数。合理的试验设计方案以及恰当的寻优方法,能够在确保模型精度的基础上实现对发动机控制参数的标定和优化[6]。
高斯过程是一个非参数的工具,广泛用于监督学习,即回归和分类问题,该方法的主要优点是能够提供不确定性估计,并从训练数据中学习噪声和平滑参数。由于高斯过程系统地结合了预测中存在的建模不确定性,因此指出高斯过程是一种强大的建模框架[7-8]。本文将基于1.5T增压发动机,通过DOE试验设计方法对VVT角度选取进行试验设计,与全因子试验设计比较,以较小的试验规模、较短的试验周期获取发动机性能数据,并以此扭矩、油耗等数据来建立高斯过程回归模型,通过回归分析预测发动机万有性能参数。
2 高斯过程回归原理与试验设计
2.1 高斯过程回归原理
高斯過程回归是一种基于贝叶斯方法的非参数概率模型。高斯过程是随机变量的集合,任意有限数量的随机变量都有一个联合高斯分布[9]。对于给定训练集D={(Xi,yi )}Ni=1={X,y},其中Xi∈RP代表p维输入向量,X={X1,X2,…,XN }即为p×N维输入矩阵,yi∈R为与Xi对应的输出标量,y为输出向量。回归的目的是通过学习样本,经过训练得到输入与输出之间的映射关系f(X),从而用新测试样本X*预测出对应的响应值y*。
简化的回归模型如下:
y=f(X)+ε (1)
y为独立变量:y={y1,y2,…,yn }
X为给定的满足多元高斯分布的N组独立学习样本:
ε为服从方差为δn2高斯分布的噪声或残差:
ε≈N( 0,δn2 ) (2)
在高斯过程回归模型中,回归函数f(X)为一个高斯过程,由其均值函数m(X)和协方差函数k(X,X' )来描述:
f(X) ~ GP(m(X),k(X,X' ) ) (3)
m(X)=E[f(X) ] (4)
k(X,X' )=E[(f(X)-m(X))(f(X' )-m(X' ) )T] (5)
为了计算简便起见,我们通常将取均值函数为零,使用实验获得真实数据进行训练后,得到输出值y的先验分布:
y~N(0,k(X,X' )+δn2 I) (6)
由定义可知,高斯过程中的任意有限的随机变量的联合分布都服从高斯分布,因此,基于新输入测试样本X*,预测输出y*与输出y的联合分布也服从高斯分布,即:
式中k( X,X )是输入样本X的协方差矩阵;k(X,X*)=k(X*,X)T是给定的新输入值X*与训练输入值X之间的协方差矩阵;k(X*,X*)为给定的新输入值X*的方差。
基于多维高斯分布的性质,在已知取得训练集D={X,y }的条件下,y*的后验分布为:
p(y*|X*,X,y)=N(m(y* ),cov(y* )) (8)
式中,y*的均值m(y* )和方差cov(y* )分别为:
m(y*)=k(X *,X )[k(X ,X )+δn2 I ]-1y (9)
cov(y* )=k(X *,X )-k(X *,X )[k(X ,X )
+δn2 I ]-1 k(X *,X )T
由定义可知,因计算中均值预设为零,高斯过程由协方差函数确定,即可以通过式(10)计算得到预测值及其方差。而协方差函数的选取是回归分析分的关键,决定了回归模型的精度[10]。
回归模型如图1所示,将发动机转速SPEED、进气相对充量RL_MESS、进气VVT参数WNWE、排气VVT参数WNWA、过量空气系数lamson、点火角zwout等对发动机性能影响较大的参数作为回归模型的输入,发动机扭矩与比油耗作为输出。使用RSM和R2評估模型拟合程度,表示回归预测值对测量数据的置信程度。
2.2 试验方案设计
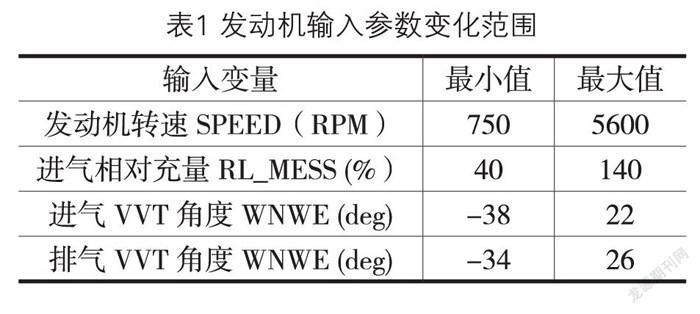
发动机输入变量的参数变化范围如表1所示,将发动机转速,进气相对充量根据控制系统相关要求进行断点设置;点火角及过量空气系数随发动机性能、燃烧稳定性、排放限值及排气温度等相关控制参数进行调整。进气VVT角度、排气VVT角度通过DOE试验设计确定,如进行一般全因子设计,采样点为5635个,该试验选择拉丁超立方抽样进行样本空间填充,设计采样点3200个,样本点减少了43.2%,节约大量时间及实验成本。
3 高斯回归模型训练与预测分析
3.1 高斯过程回归模型训练
按照DOE试验设计列表,在发动机台架上进行试验数据收集。相关发动机试验边界是:通过控制过量空气系数,使排气温度或三元催化器中部温度保持在设定的温度上限值以下;通过调节点火角,使各缸平均AI50保持在8附近或者爆震边界。将收集的试验数据导入MATLAB,通过应用回归训练进行回归训练,选用5倍交叉验证,以防止过拟合,基函数及核函数选择及回归模型评价指标均方根误差RMSE、平均误差MAE如下表2所示,从表2数据可知,扭矩回归模型和比油耗回归模型均具有较高拟合度。
图2a是比油耗百分比误差分布图,比油耗模型的百分比误差呈正太分布,均值为0,标准差为0.73%;图2b是比油耗的残差图,比油耗在500g/kwh以内的残差小于50g/kwh,在比油耗大于500g/kwh的点,部分残差较大,主要是因为小负荷区域的发动机燃烧不稳定及测量误差等因素导致模型噪声大。
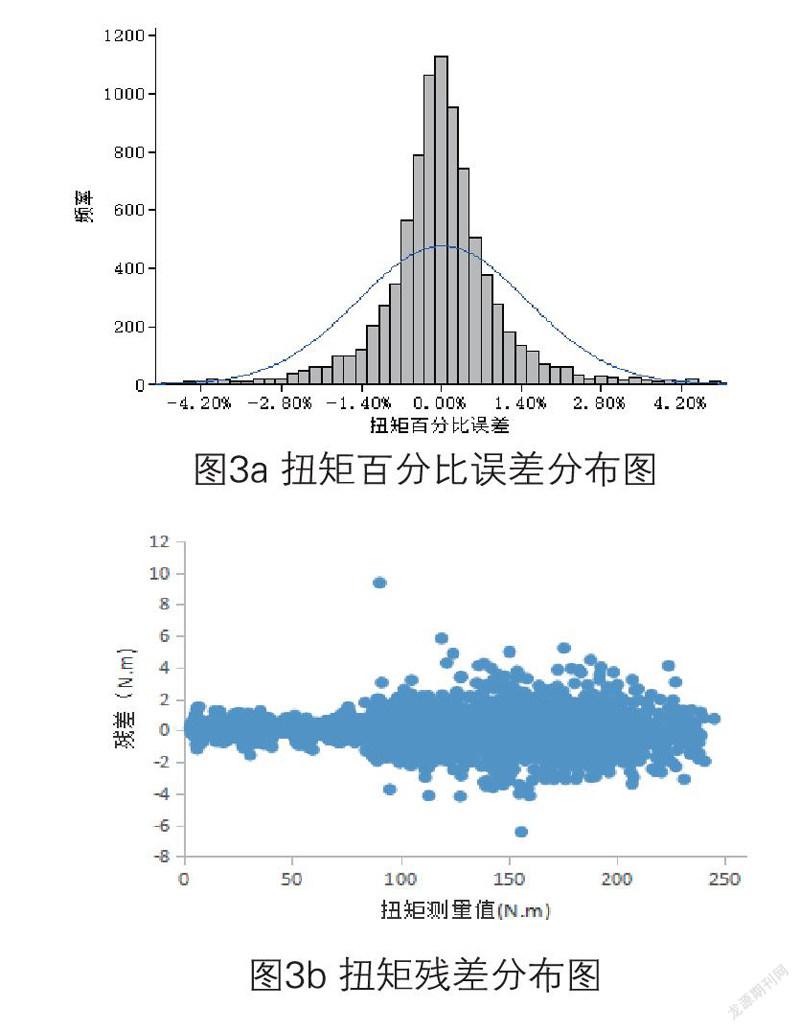
图3a为扭矩模型的百分比误差分布图,均值为0,标准差为1.48%;图3b为扭矩残差图,扭矩残差绝对值不超过10N.m,百分比误差超过5%的发动机工况点主要分布在相对进气系数rl_mess少于25%的区域,主要是因为该区域发动机扭矩较少,残差微小波动会引起较大的百分比误差。通过对回归模型的百分比误差及残差值分析,扭矩回归模型和比油耗回归模型具有较高的拟合度,能有效地用于发动机的性能参数预测。
3.2 发动机性能预测与试验对比
发动机完成标定后,进行发动机的万有性能测试;分别通过扭矩高斯回归模型和比油耗高斯回归模型,使用与万有性能测试相同的输入变量参数进行发动机性能预测,并对预测值与试验测试值进行对比。
图4a是扭矩高斯回归模型的响应图,扭矩点分布在标准曲线两侧;从图4b扭矩残差分布图可以看出,扭矩残差分布在-5N.m与7N.m之间,具有较高的预测精度,说明模型精度符合扭矩的预测需求。
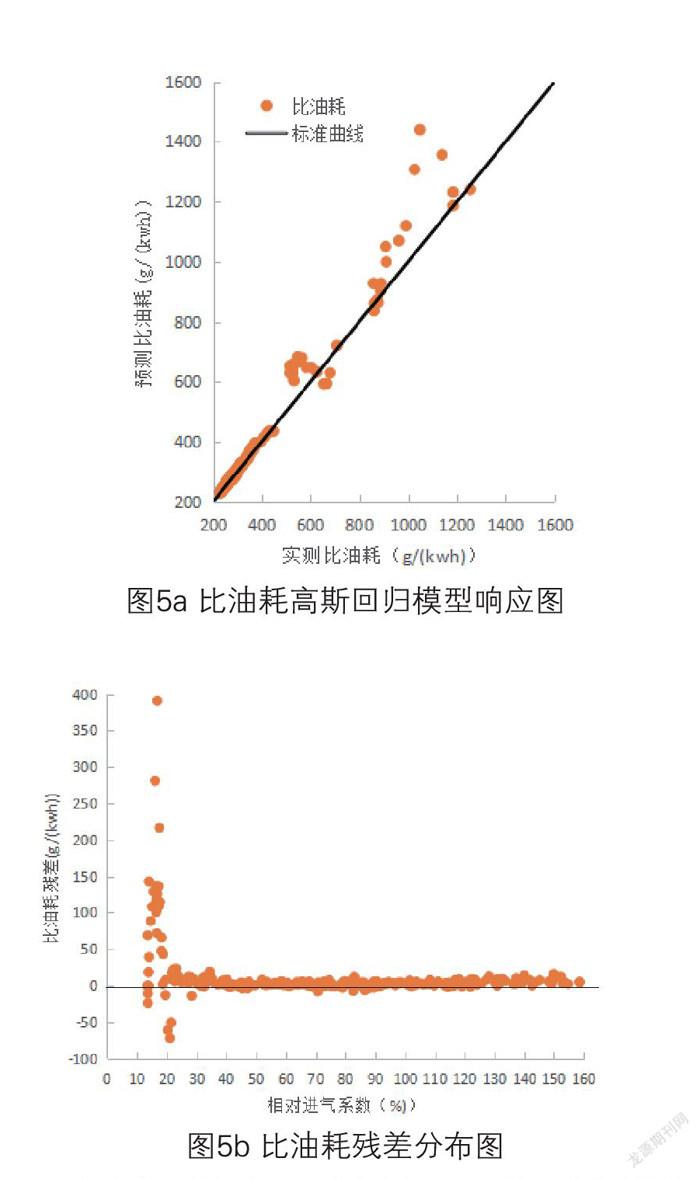
图5a是比油耗高斯回归模型响应图,比油耗在500g/kw.h以内,预测比油耗预测点分布在标准曲线两侧,具有较好的预测精度;在大于500g/kw.h的比油耗预测点大部分居于标准曲线之上,从图5b比油耗残差分布图可以看出,这些偏差较大的点均来自于负荷较低的区域,原因是发动机小负荷区域的比油耗测量误差较大,导致模型预测值标准差加大。
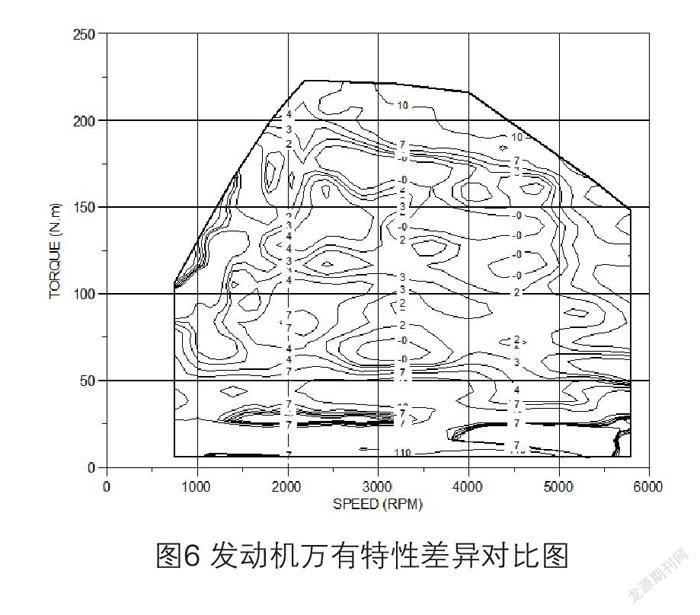
通过分别使用台架测试数据和模型预测数据分析发动机万有特性,并对其差值进行万有特性曲线绘制。图6是发动机测试值万有特性与预测值万有特性的差值对比图,图中差值大部分区域小于10g/kw.h,在小负荷(扭矩小于20N.m)区域,因误差较大,差值为110g/kw.h。
4 总结
采用拉丁超立方抽样方法进行科学的试验设计,在测试台架上以较少测量次数获取有代表性的训练数据,基于高斯过程回归构建了发动机扭矩及油耗的回归模型,通过与实测数据对比,模型预测具有较好的预测精度,在发动机扭矩25N.m以上区域,油耗偏差最大不超过5%,满足发动机性能的预测精度要求。但是,在小负荷区域,因测量误差加大,模型预测偏差较大,还需加大样本测量或针对该区域建立新的回归模型,重新训练模型,提高模型预测精度,减少泛化误差。总之,高斯过程回归模型能有效地基于小样本数据预测发动机性能,应用高斯过程回归模型能有效地减少发动机试验测试工作量,为类似发动机性能参数优化提供参考。
参考文献:
[1]Richard Fiifi Turkson,Fuwu Yan,Mohamed Kamal Ahmed Ali, Jie Hu. Artificial neural network applications in the calibration of spark-ignition engines: An overview [J]. Engineering Science and Technology,an International Journal,2016 (19):1346–1359.
[2]M.R. Kianifar,L.F. Campean, D. Richardson,Sequential DoE framework for steady state model based calibration [J]. SAE Int. J. Engines 2013 (6):843–855.
[3]Pak Kin Wong, Xiang Hui Gao, Ka In Wong,Chi Man Vong. Efficient point -by-point ngine calibration using machine learning and sequential design of experiment strategies[J]. Journal of the Franklin Institute 2018(355):1517-1538.
[4]S. Jiang,D. Nutter,A. Gullitti,Implementation of Model-Based Calibration fora Gasoline Engine [J],SAE International, 2012.
[5]周廣猛,刘瑞林,李骏.基于模型的电控发动机标定技术[J].汽车技术,2011 (1) :1-5.
[6]张文.基于高斯过程回归模型的发动机VVT参数 标定[J].工业控制计算机. 2019,32(09):4-8.
[7]Mahdi Zarghami S. Hassan Hosseinnia Mehrdad Babazadeh. Optimal Control of EGR System in Gasoline Engine Based on Gaussian Process[J]. IFAC Papers OnLine, 2017 (50):3750–3755.
[8]Benjamin Berger ,Florian Rauscher,and Boris Lohmann. Analysing Gaussian Processes for Stationary Black-Box Combustion Engine modelling[J]. Proceedings of the 18th World Congress The IFAC Milano (Italy) 2011:10633-10640.
[9]Rasmussen, C.E. and Williams,C.K.I. . Gaussian Processes for Machine Learning. The MIT Press(2006).
[10]Arun C. Ravindran,Sage L. Kokjohn .Combining machine learning with 3D-CFD modeling for optimizing a DISI engine performance during cold-start[J].Energy and AI 2021 (5) 100072:1-18.
闫雪华
毕业于广西大学,材料学专业,硕士学位。现就职于上汽通用五菱汽车股份有限公司技术中心,任发动机设计主任工程师。主要从事汽油发动机设计开发,已发表论文3篇。
专家推荐语
王必璠
东风商用车技术中心
平台总师 研究员级高级工程师
论文采用拉丁超立方抽样建立试验样本,并构建高斯过程回归模型,以发动机动力性和经济性为目标,对发动机进排气进行了标定优化,取得了预测精度5%的预期效果。模型构建和数据处理方法对行业有积极的借鉴意义。

