基础摩擦滑移隔震结构起滑加速度研究

江云帆，郭子雄,2，刘 阳,2

(1. 华侨大学土木工程学院，福建，厦门 361021；2. 华侨大学福建省结构工程与防灾重点实验室，福建，厦门 361021)

基础隔震是一种能有效减小房屋地震需求，减轻强震作用下房屋损伤的技术。基础隔震体系主要包括纯摩擦滑移隔震体系[1]、恢复力滑移隔震体系[2]、摩擦摆隔震体系[3 − 6]、铅芯橡胶隔震体系[7 − 10]和高阻尼橡胶隔震体系[11 − 12]等。其中，纯摩擦滑移隔震体系因其造价低廉，施工简单的优点，常应用于村镇建筑中。该体系仅需在上部结构与基础间设置一层摩擦滑移界面，其工作原理是：强震作用下，上部结构沿摩擦界面水平滑动，界面的动摩擦力限制了传递至上部结构的地震力大小，同时摩擦阻尼耗散了地震能量，从而达到减震的目的。

国内外学者针对纯摩擦滑移隔震结构的隔震性能及不同材料滑移界面的摩擦性能开展了一系列试验研究。Li[1]提出以沙粒为隔震层材料，并开展了5个滑移隔震砌体房屋模型的振动台试验，研究发现：设置隔震层能有效防止房屋在强震下倒塌。楼永林等[13]对以石墨、砾砂和石蜡为隔震层材料的隔震砖墙试件开展了振动台试验，研究发现：石墨适用性最好，带石墨隔震缝砖墙试件起滑加速度为0.2g～0.3g。Qamaruddin等[14]对以摩擦系数分别为0.25、0.34和0.41的石墨粉，干砂和湿砂为隔震层材料的隔震砖砌房屋及相应固定支座房屋模型开展了振动台试验，结果表明：隔震缝能有效降低房屋加速度响应。Nanda等[15 − 16]对绿色大理石-高密度聚乙烯、双层绿色大理石、绿色大理石-土工合成材料和绿色大理石-橡胶隔震缝界面开展了摩擦性能试验研究，结果表明：竖向压应力，滑移距离和速度对界面动摩擦系数均基本无影响，四种界面的动摩擦系数分别为0.08、0.09、0.11和0.16。荣强等[17]对聚四氟乙烯-不锈钢板滑移隔震界面开展了力学性能试验研究，结果表明：界面滑动摩擦系数随竖向压力增大而减小，随滑动速度增大而增大，涂抹硅脂明显降低摩擦系数。基于试验结果建立了新的界面摩擦力模型。

此外，国内外学者采用数值方法对纯摩擦滑移隔震结构的动力响应特性进行了研究。常用的数值模型为由上部和基础质点组成的两自由度体系。Mostaghel等[18]首次采用两自由度模型模拟滑移隔震结构，研究了简谐波激励下，模型参数及简谐波特性对隔震结构峰值加速度和滑移位移响应的影响规律。Westermo等[19]研究发现简谐波激励下，隔震结构呈现出3种周期性响应状态，即持续固定支座状态(stick-stick)、断续滑动状态(stick-slide)和持续滑动状态(slide-slide)，提出了结构由持续固定支座状态转换至断续滑动状态先决条件的计算公式。Iura等[20]提出了简谐波激励下，隔震结构由断续滑动状态转换至持续滑动状态先决条件的计算公式。Hu等[21]提出了简谐波激励下，隔震结构持续滑动状态最大伪加速度响应的理论解。Mostaghel等[22]研究了在El Centro和Olympia地震动记录激励下，隔震结构的动力响应特性。毛利军等[23]对地震动激励下，不同参数隔震结构的反应谱特性开展了研究，研究表明：采用反应谱法对隔震结构进行初步设计可行，精度满足工程要求。隔震体系上部结构绝对及相对加速度、相对位移反应谱的变异系数均明显小于传统结构反应谱。

国内学者建议的村镇滑移隔震结构设计性能目标为“小震不滑，中震起滑，大震限位”。然而现有研究中，尚未见有关地震动激励下，纯滑移摩擦隔震结构由持续固定支座状态转换至断续滑动状态先决条件，即起滑条件的研究。本文采用两自由度体系模拟滑移隔震结构，以匹配于规范设计反应谱的6组地震动集为输入，研究了地震动参数和隔震结构参数对起滑加速度的影响规律。采用分段拟合的方法建立了起滑加速度计算公式。结果可供滑移隔震结构的起滑条件研究和工程设计提供参考。

1 两自由度滑移隔震结构模型及起滑加速度求解流程

采用两自由度模型模拟基础滑移隔震结构，如图1所示。该模型由通过阻尼单元及水平弹簧单元相连接的上部及基础质点组成，基础质点设置于允许水平向滑动的滑移摩擦面上，基础质点与摩擦面间摩擦力符合库仑摩擦定律。

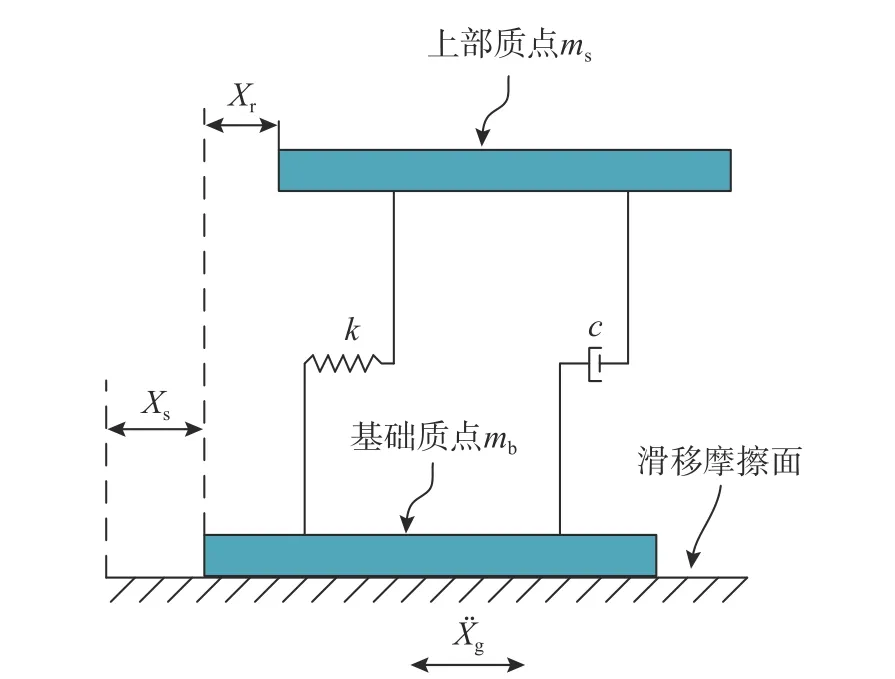
图1 基础滑移隔震结构动力模型Fig.1 Dynamic model of sliding base isolation structure

地震动激励下，隔震结构有两种阶段。当上部及基础质点的惯性力之和小于滑移面摩擦力时，结构处于固定支座阶段。此时结构滑移位移Xs等于0，其基础质点与地面同步振动，其上部质点的动力平衡方程为：

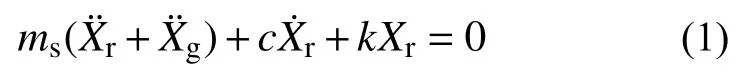
当上部及基础质点的总惯性力等于或大于摩擦力后，模型进入滑动阶段，此时整体模型及上部质点的动力平衡方程为：

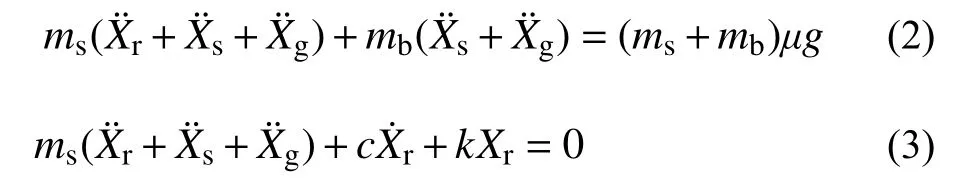
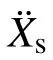
当地震动峰值加速度较小时，结构在整个地震时程中均未滑动，均处于固定支座阶段，此时结构的状态为持续固定状态；当峰值加速度足够大时，地震时程中结构交替进入固定和滑动阶段，此时结构的状态为断续滑动状态。两种状态的临界地震动峰值加速度即为起滑加速度。达到起滑状态时，结构上部与基础质点惯性力之和的峰值时程响应等于滑移面摩擦力，且此时结构滑动加速度近似为0，即：

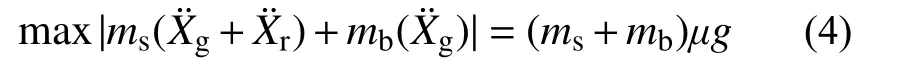
将式(4)两端除以ms+mb可得：

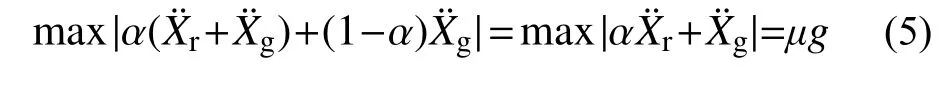
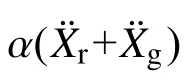
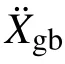
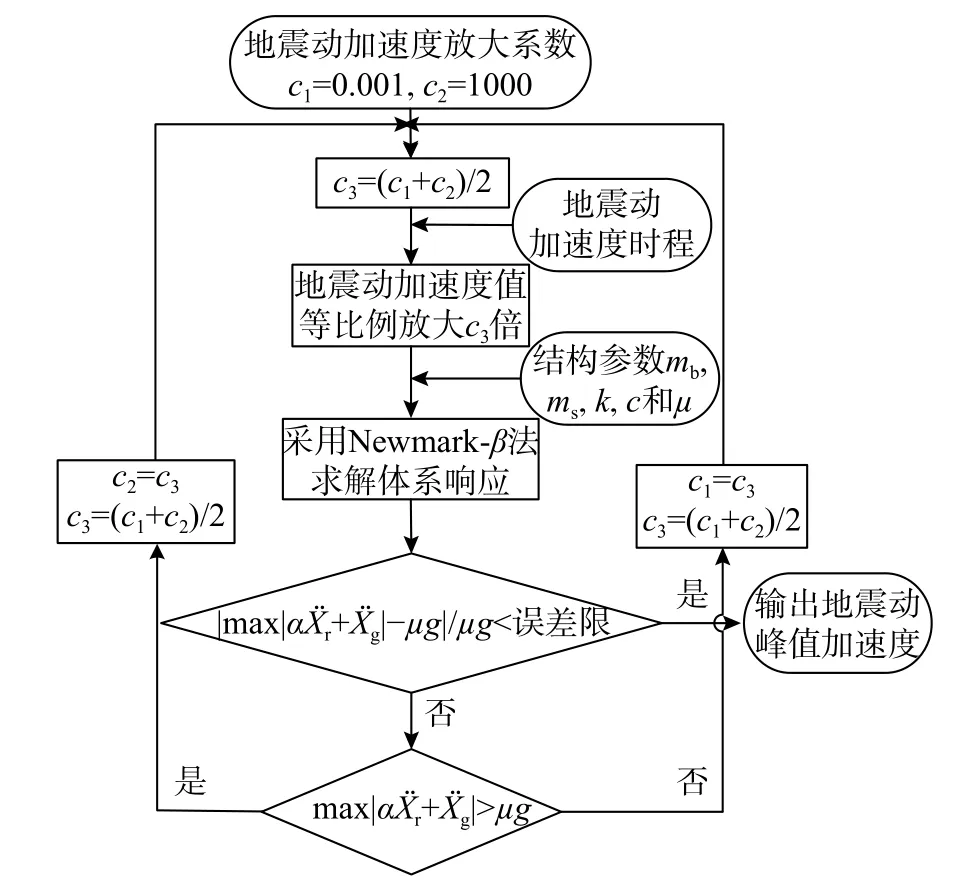
图2 起滑加速度求解流程图Fig.2 Calculate procedure of the acceleration for the occurrence of sliding

2 地震记录选取与模型参数

采用Pant等[24]建议的方法选取共6组，每组20条匹配于中国抗震规范[25]中设计反应谱的地震记录。地震记录参数包括地震记录类型及目标反应谱特征周期，地震记录包括近断层脉冲型和非脉冲型记录，通过Baker[26]提出的方法区分。规范中影响特征周期的参数主要为设计地震分组和场地类别。本文所选取目标设计反应谱的场地类别为第Ⅰ类、第Ⅱ类和第Ⅲ类，设计地震分组为第一组、第二组和第三组。各组地震记录集的地震记录类型、目标反应谱地震分组、场地类别及特征周期列于表1。

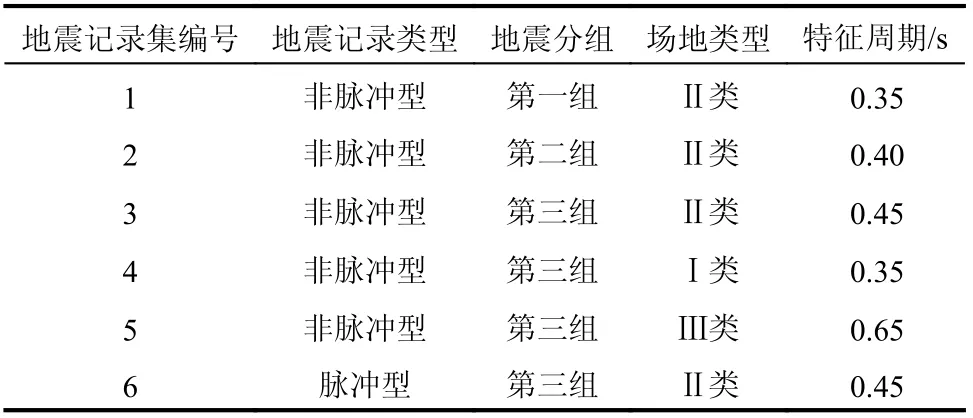
表1 所选地震记录参数Table 1 Parameters of the selected ground motions

地震记录选取分两步：

1) 从太平洋地震中心(PEER)强震数据库中选取6组地震记录。采用30 m覆盖层平均剪切波速Vs30作为判别场地类别的指标，基于吕红山等[27]的研究，第Ⅰ类、第Ⅱ类和第Ⅲ类场地地震记录Vs30的取值范围分别取>510 m/s、260 m/s～510 m/s和150 m/s～260 m/s。采用震级和震中距(观测点到震中的水平距离)作为判别设计地震分组的指标，Ⅱ类场地第一组、第二组和第三组地震记录震级及震中距的取值范围根据高孟潭[28]提出的衰减关系模型确定，其表达式为：

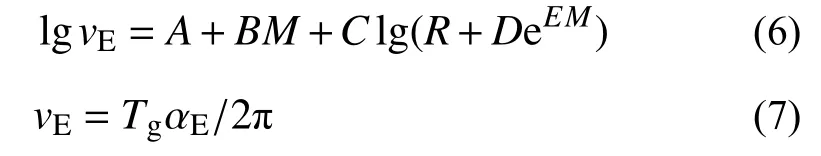
式中：vE为峰值速度；R和M分别为震中距和震级；A、B、C、D和E为回归系数，本文选用东部强震区长轴对应的系数；αE为峰值加速度，本文取目标设计反应谱对应的设计基本加速度0.15g；Tg为反应谱特征周期。所选地震记录震级均在4级～7级，震中距在0 km～200 km，以满足衰减关系模型的适用范围。

2) 采用Hancock等[29]提出的方法对第一步中所选取地震记录进行调整以生成匹配于目标反应谱的地震记录。该方法的原理是通过在时域内对地震波加速度时程叠加小波来生成兼容于反应谱的地震波。所生成6组地震波集平均加速度反应谱与目标设计反应谱的对比如图3所示。

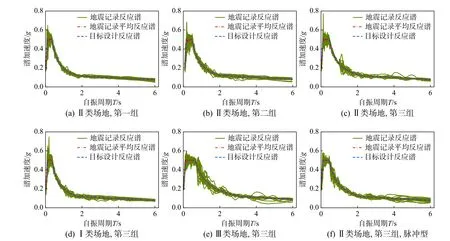
图3 所选地震记录加速度反应谱与目标设计反应谱对比Fig.3 Comparison between the acceleration response spectrum of selected earthquake records and target design spectrum

模型参数主要包括动摩擦系数µ、质量比α和上部结构自振周期T。前期摩擦滑移隔震体系的相关试验研究中[13 − 17]，滑移界面动摩擦系数的取值在0.07～0.41，基于此动摩擦系数取0.05、0.15、0.25、0.35和0.45。质量比取0.6、0.7、0.8和0.9。上部结构自振周期取0.02 s～6 s内的112个周期。上部结构阻尼比取常用的0.05。

3 参数分析

3.1 上部结构自振周期的影响

结构平均起滑加速度与自振周期典型的关系曲线如图4所示。由图可知，曲线可分为4段，各段的自振周期取值范围分别为：T=0 s～0.1 s、T=0.1 s～Tg、T=Tg～5Tg和T>5Tg。前三段分别对应于相应固定支座结构加速度设计反应谱的上升段、加速度敏感段和速度敏感段。随自振周期的增大，起滑加速度在曲线第一段内近似呈线性降低，第二段基本保持不变，第三段增大，第四段中先增大而后基本保持不变。前三段中起滑加速度值与相应固定支座结构反应谱值成反比。这是因为上部质点加速度峰值响应值越大，结构越易起滑。第四段中当自振周期较小时，起滑加速度同样与反应谱值成反比，但当自振周期足够大时，由于上部结构惯性力响应较小，起滑力主要由基础质点惯性力响应贡献，起滑加速度值与反应谱值无明显相关性，其值基本保持不变。

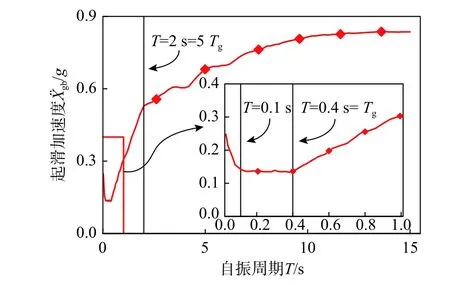
图4 典型平均 曲线(Ⅱ类场地，第二组，α=0.7，µ=0.25)Fig.4 Typical average curve (Soil type Ⅱ,group two, α=0.7, µ=0.25)

3.2 摩擦系数的影响

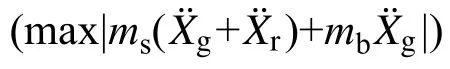
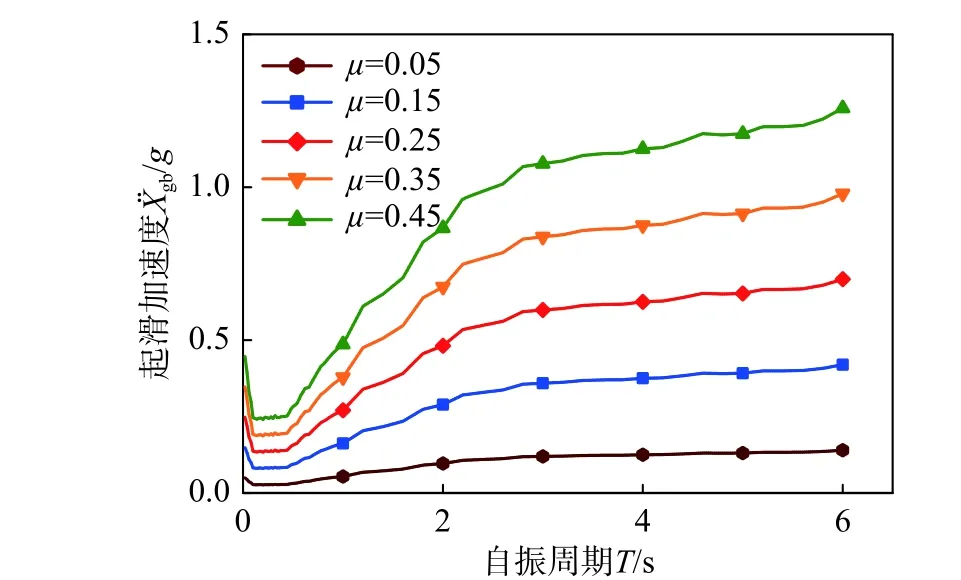
图5 摩擦系数对平均 曲线的影响(Ⅱ类场地，第三组，非脉冲型地震，α=0.7)Fig.5 Effect of the friction coefficients on the average curves (Soil type Ⅱ, group three, non-plus like ground motion, α=0.7)

3.3 质量比的影响

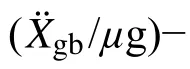
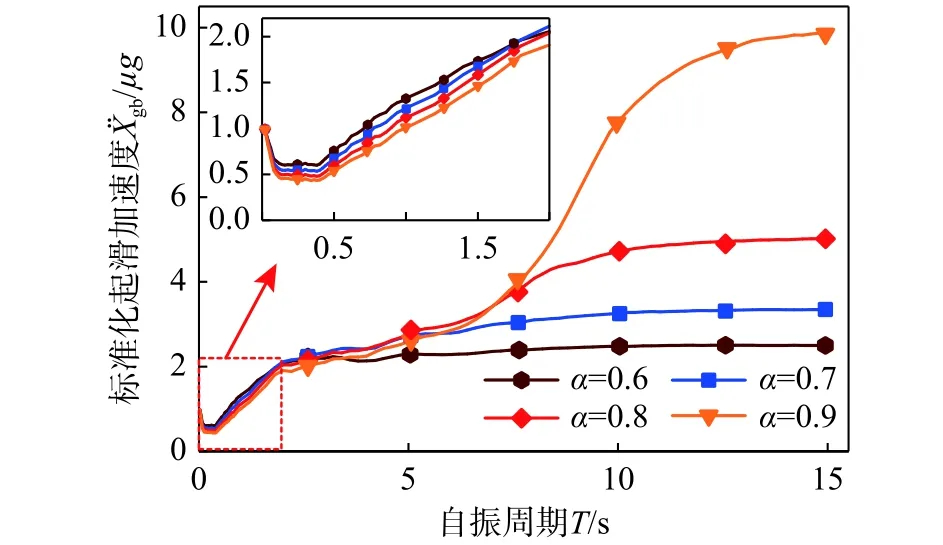
图6 质量比对平均 曲线的影响(Ⅱ类场地，第二组)Fig.6 Effect of mass ratios on the average curves(Soil type Ⅱ, group two)

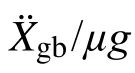
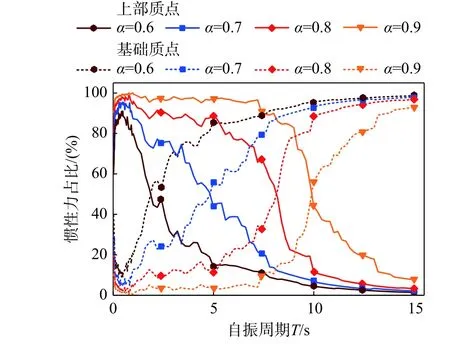
图7 不同质量比结构起滑时上部与基础质点惯性力占比(Ⅱ类场地，第二组)Fig.7 Proportion of the inertial force of the top and foundation mass at the initial of sliding for structures with different mass ratios (Soil type Ⅱ, group two)

3.4 特征周期的影响

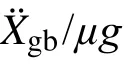
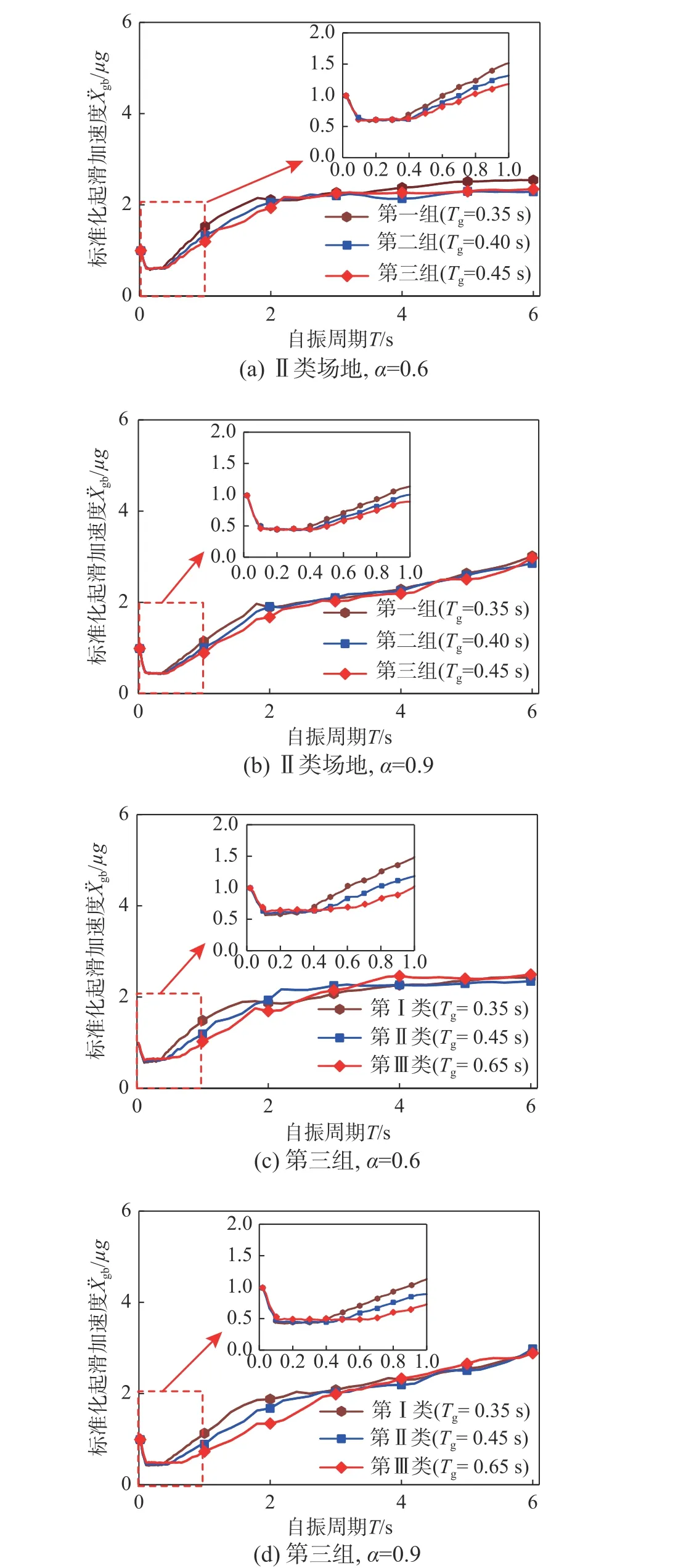
图8 特征周期对平均 曲线的影响Fig.8 Effect of characteristic periods on the average curves

3.5 近断层脉冲的影响

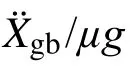
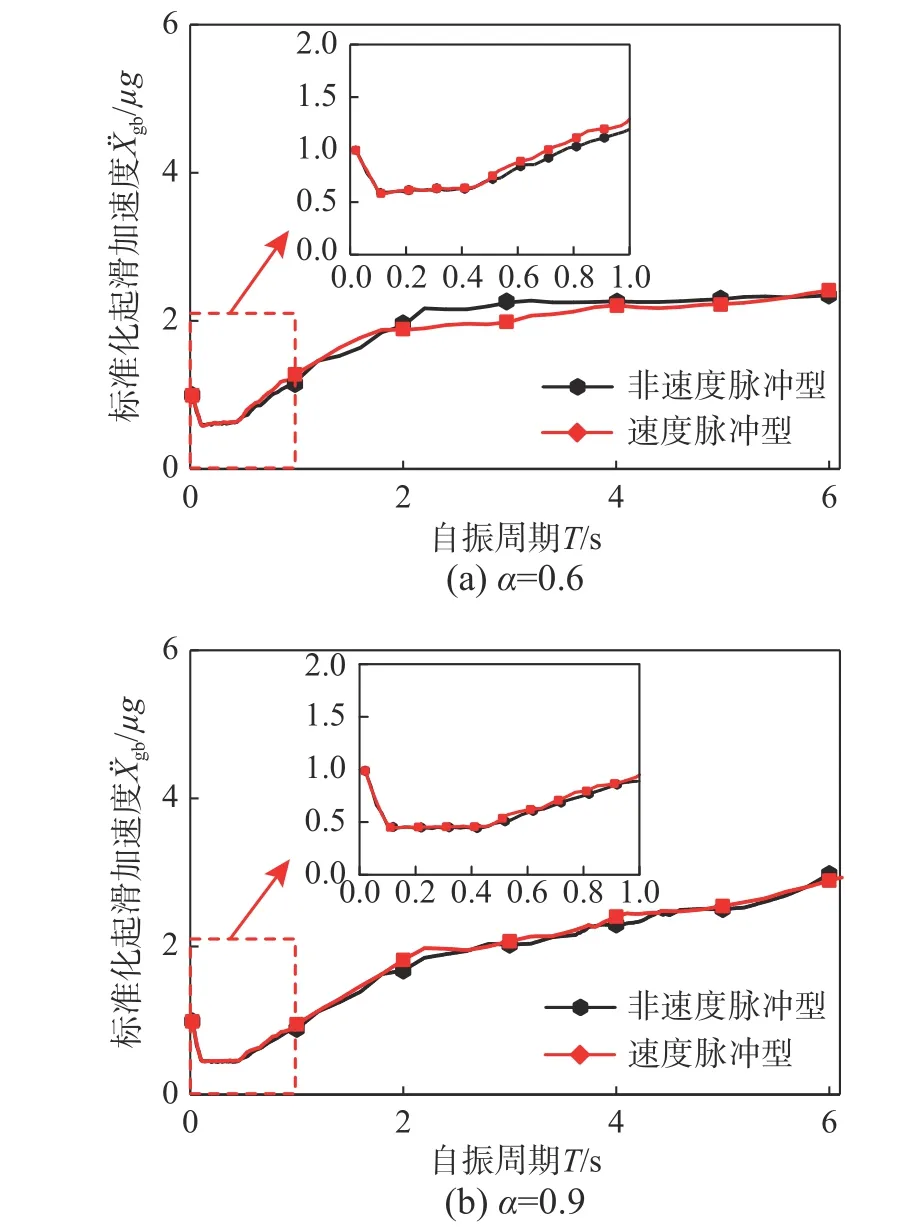
图9 近断层脉冲对平均 曲线的影响Fig.9 Effect of near-fault pulse on average curves

4 起滑加速度计算公式建立

基于计算所得平均标准化起滑加速度−自振周期曲线，采用分段拟合方法建立了不同参数曲线的计算公式，如下：

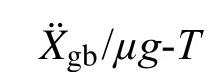
表2 曲线拟合公式回归系数取值Table 2 Regression coefficient values of fitting formula for curves

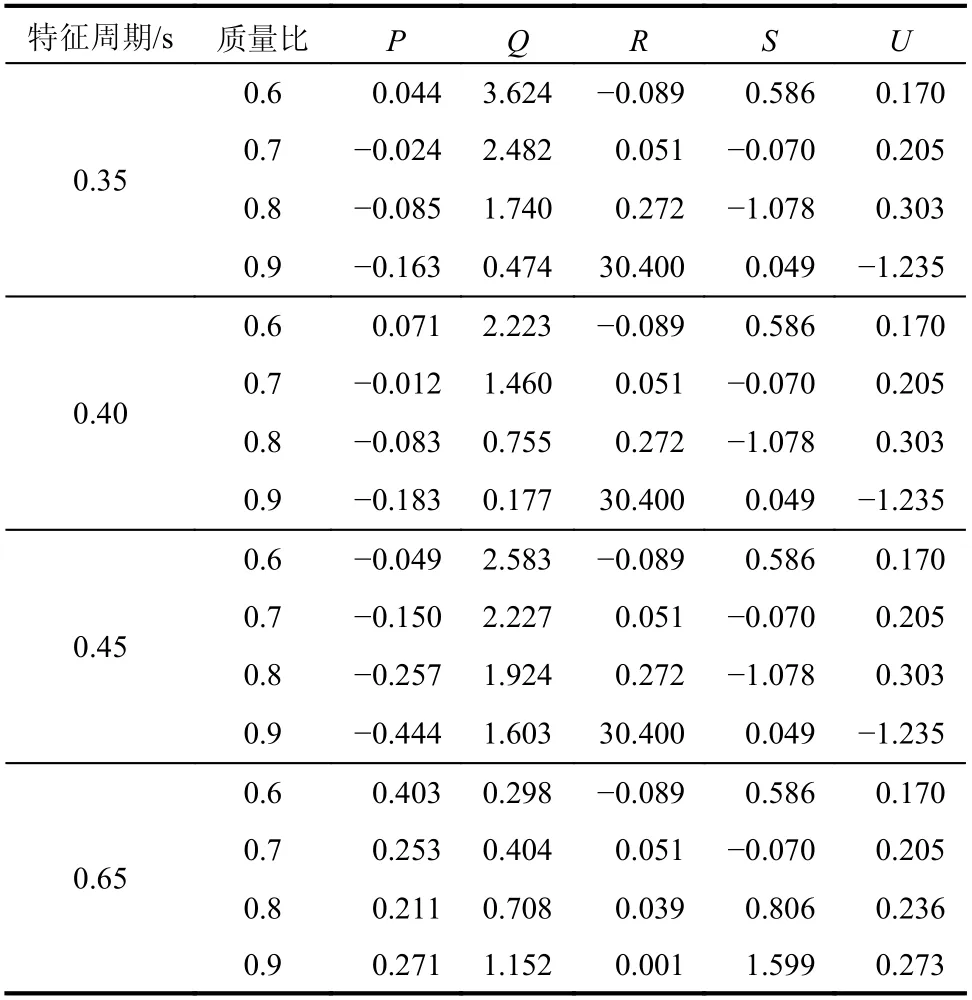
表2 曲线拟合公式回归系数取值Table 2 Regression coefficient values of fitting formula for curves

特征周期/s 质量比 P Q R S U 0.35 0.6 0.044 3.624 −0.089 0.586 0.170 0.7 −0.024 2.482 0.051 −0.070 0.205 0.8 −0.085 1.740 0.272 −1.078 0.303 0.9 −0.163 0.474 30.400 0.049 −1.235 0.40 0.6 0.071 2.223 −0.089 0.586 0.170 0.7 −0.012 1.460 0.051 −0.070 0.205 0.8 −0.083 0.755 0.272 −1.078 0.303 0.9 −0.183 0.177 30.400 0.049 −1.235 0.45 0.6 −0.049 2.583 −0.089 0.586 0.170 0.7 −0.150 2.227 0.051 −0.070 0.205 0.8 −0.257 1.924 0.272 −1.078 0.303 0.9 −0.444 1.603 30.400 0.049 −1.235 0.65 0.6 0.403 0.298 −0.089 0.586 0.170 0.7 0.253 0.404 0.051 −0.070 0.205 0.8 0.211 0.708 0.039 0.806 0.236 0.9 0.271 1.152 0.001 1.599 0.273

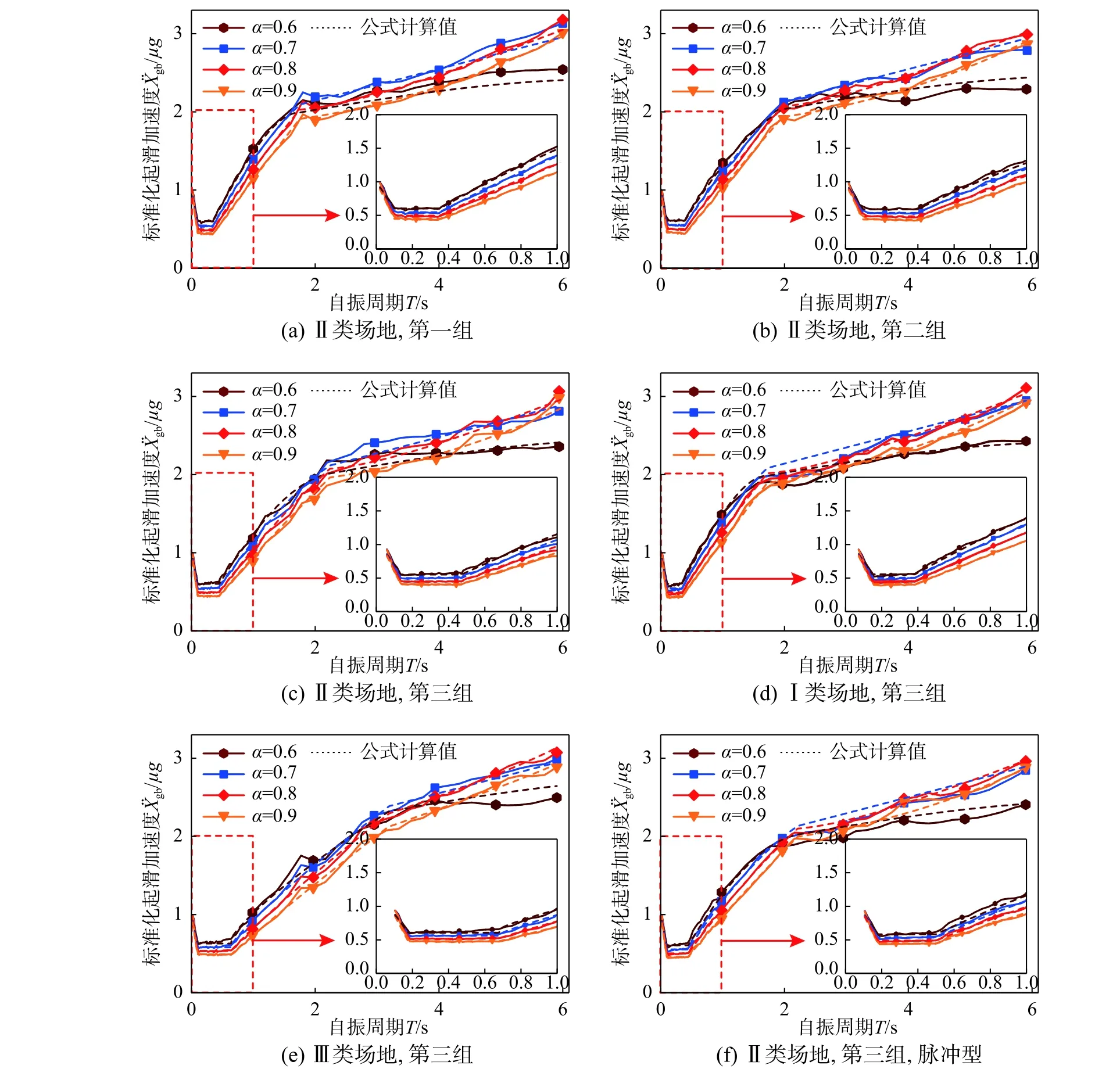
图10 拟合公式与时程分析计算所得曲线对比Fig.10 Comparison between the curves computed using the fitting formula and those computed from time history analyses

隔震结构设计时，可根据所提出公式求解结构在多遇地震和设计地震作用下的起滑摩擦系数，进而确定满足“小震不滑，中震起滑”设计原则的摩擦系数取值范围，以指导隔震层材料的选用。

5 算例验证

为验证拟合公式估算多自由度结构起滑加速度的准确性，以某上部结构为3层和9层的滑移隔震结构为算例进行分析。所取结构的层质量及层刚度沿高度方向均匀分布，且基础质量与层质量相等，即mb=ms1=ms2=···msn，k1=k2=···kn(n为楼层数)。层刚度均取7500 kN/mm。3层和9层结构层质量分别取1.5 t和1.86 t，以使其上部结构第一振型自振周期分别等于0.2 s和0.6 s。各阶振型的阻尼比均取0.05。采用拟合公式计算起滑加速度时，将多自由度体系等效为两自由度体系，等效体系上部结构自振周期取相应固定支座多自由度结构第一振型自振周期。质量比取相应固定支座多自由度结构第一振型参与质量与隔震结构总质量之比：

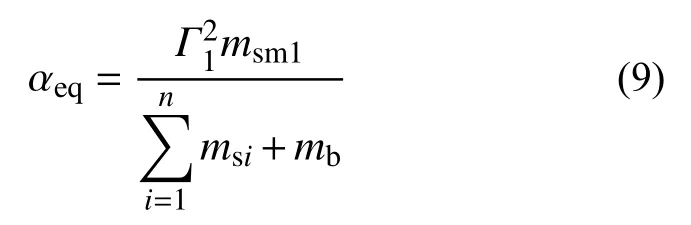
式中，Γ1和msm1分别为相应固定支座多自由度结构第一振型参与系数和第一振型主质量。根据式(9)求得3层和9层算例的等效质量比分别为0.6856和0.7665。

6组所选地震动集激励下，采用时程分析及式(8)求解出的算例平均标准化起滑加速度值列于表3。由表可知，两者差值在5%之内，表明所提出公式较合理。

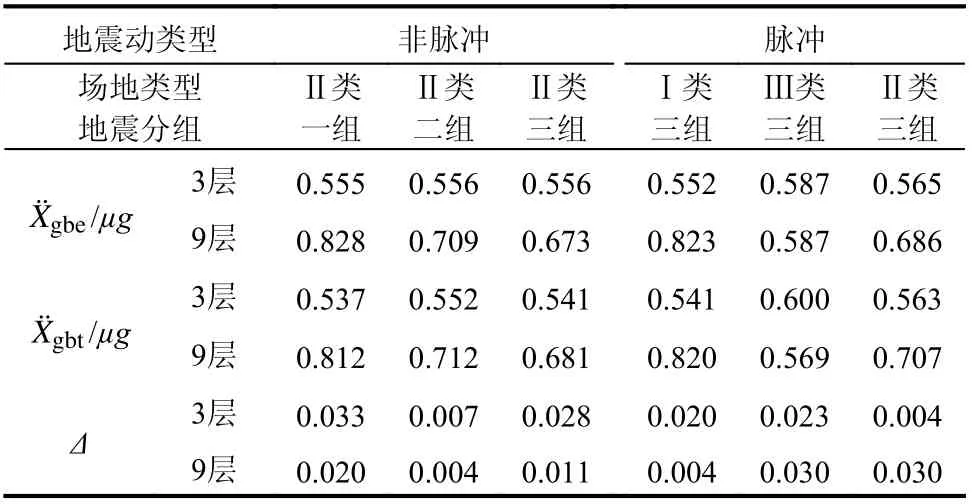
表3 公式与时程分析结果对比Table 3 Comparation between the results obtained using fitting formula and time history analyses

隔震结构设计时，若所设计隔震结构的动力特性与本文3层算例相近，且所在地区的设计基本地震加速度为0.15g，场地类型为Ⅱ类(设计地震分组为第二组)。由式(8)算得多遇和基本烈度地震作用下结构起滑时的摩擦系数分别为0.096和0.270，则所设计房屋隔震层材料的摩擦系数选择范围在0.096～0.270。

6 结论

本文以滑移隔震结构为对象，研究了结构参数和地震波参数对其起滑加速度的影响规律，并建立了起滑加速度计算公式。所考虑参数范围内，研究结果如下：

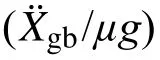
(2) 当自振周期小于1.4 s时，相同自振周期结构的起滑加速度随质量比的减小而增大。自振周期大于7.8 s时，相同自振周期结构的起滑加速度随质量比的减小而减小。起滑加速度随摩擦系数的增加而等比例增加。

(3) 结构自振周期在设计反应谱速度敏感段内时，起滑加速度随反应谱特征周期增大而减小，特征周期对其余自振周期结构起滑加速度影响较小。当相应固定支座结构加速度反应谱较接近时，结构在脉冲型和非脉冲型地震动集激励下的起滑加速度相差较小。

(4) 基于参数分析结果，采用分段拟合的方法建立了起滑加速度计算公式。公式计算结果与多自由度结构算例时程分析计算结果吻合良好。公式可为滑移隔震结构的隔震层摩擦系数取值提供参考。