基于加速度传感器的检定轻墩铁路桥梁横向位移新方法及振动台试验验证

陈令坤，徐 祥，蒋丽忠，张清华，张 楠，李 乔

(1. 扬州大学建筑科学与工程学院，江苏，扬州 225127；2. 西南交通大学土木工程学院，四川，成都 610031；3. 中南大学高速铁路建造技术国家工程实验室，长沙 410075；4. 北京交通大学土木建筑工程学院，北京 100044)

铁路以其运输能力强、成本低、效率高的优点成为许多国家货运的发展方向。一方面由于列车轴重的提升加大了桥梁上的荷载；另一方面，随着列车速度的提升，桥梁动力响应增大，大部分轻型墩桥梁墩顶横向振幅过大，严重影响行车安全阻碍货运发展[1]。截至2019年底，我国铁路货运累计达43.81亿吨[2]，但很多桥梁在质量上却存在很多问题，桥梁的维护工作的压力与日俱增。如何替代昂贵的维护方案，帮助铁路主管部门准确把握桥梁状态已成为当前的热门研究课题。近十年来随着新技术的快速发展，传感器在桥梁健康监测领域中的应用已日趋完善[3 − 5]。传感器能够实时感知结构响应，并向终端反馈结构状态以帮助桥梁管理者解决结构存在问题，阻止发生事故。

结构健康监测通常基于传感器观测结构频率、固有振型、挠度和模态应变能量的变化判断结构状态[6 − 7]。然而基于观测结构频率、固有振型、模态应变能量变化的方法，通常需要养护人员对桥梁结构有深入的了解和充分的理论知识，这是大部分铁路管理人员所不具备的。因此，基于结构位移性能的变化判断结构状态，能够帮助铁路管理人员直观地了解结构状态。

早期线性可变微分传感器(LVDT)在桥墩动力试验及在役位移检定中扮演了重要角色。然而这类传感器需要固定的参考系，使用存在一定的局限性，特别是对于高墩桥梁[8 − 9]。所以一些能够克服克服需要参考点局限性的新型无参考传感技术被引入结构健康监测系统中。Stiro等[10]和Psimoulis等[11]提出了一种非接触式机器人全站仪(RTS)和经纬仪定位系统(TPS)来捕捉铁路桥梁位移响应的方法。然而，该方法依赖于有利的大气条件且局限于峰值位移在2.5 mm～6 mm的相对刚性桥梁。非接触式激光多普勒测振系统(LDV)来检定桥梁位移虽然能克服上述缺点，但这种测量手段并不适合长期监测[12]。全球定位系统(GPS)现在可用于桥梁和其他大型工程结构的实时监测，但需要与复杂的桥梁模型相结合分析[13 − 14]，这不利于铁路管理人员的实际操作。

此外，基于视觉和光学技术的检定系统同样给桥梁位移检定带来一定的可能性。部分学者提出了一种利用摄影测量图像分析原理对桥梁难以检定的位置进行结构位移监测的方法[15]。这种监测方法能够进行高分辨率的动态测量，有着低成本、实时测量、易于安装操作以及抗干扰能力强的优点，但其过度依赖于大气环境，难以持续稳定地提供桥梁实时位移数据。基于此，发展出无人机联合摄影测量图像处理技术[16]。近年来大数据及人工智能的新算法开始在桥梁健康监测领域开始尝试[9,17 −18]。但是这些新技术需要精确的数值建模甚或孪生技术，目前在重要的桥梁(如笔者参与的英国的福斯公路桥(Forth Road Bridge)和昆斯费里大桥(Queensferry Crossing))中使用。对于国内大量的轻型墩中小跨度铁路桥，需要一种更为方便可靠的监测和检定方法。

本文提出了一种基于加速度传感器进行桥梁位移检定的方法，避免了上述缺点。直流加速度传感器能够稳定持续地监测结构，采集结构响应，其外壳坚固能确保在低劣的环境中应用。加速度传感器有着广泛的监测频率范围，确保数据采集的完整性和低噪声。本文利用加速度传感器采集铁路桥墩高频动态数据和低频伪静态数据，对墩顶横向位移进行检定。其特点是不需要固定参考点、不依靠良好的天气条件、成本低、可靠性好，能够实时长期监测桥墩各频域内的位移响应。

1 位移检定基本理论

1.1 桥梁横向总位移

铁路桥梁会受到由动态和伪静态组成的横向位移。动态分量包含由列车引起的频率大于0.5 Hz的高频零均值响应[19]。此外，列车通过桥梁上具有一定不均匀性的轨道部分，其质心可能横向偏移，产生偏心垂直载荷[20 − 21]。这种偏心垂直载荷可能导致桥梁的伪静态横向偏转引起频率低于0.5 Hz的低频位移响应[22]。

1.2 动态位移检定

使用有限脉冲响应(FIR)滤波器提取有限时间间隔内加速度线性组合来检定位移[23]，如式(1)所示，该方法可避免因边界条件的不确定性带来的积分误差。

正则化函数能抑制重构位移中的噪声干扰分量[24 − 25]。最优正则化因子经过Lee等[23]的推导得出公式为：

式中，N代表有限时间窗口内的数据点的数量。当时间窗的平均大小是传感器数据采集频率最大周期的3倍时，最优正则化因子更为准确。

1.3 伪静态位移检定

Fisher[26]提出用一个加速度计(单轴)来测量物体的横向加速度并计算弯曲角度的方法，如图1所示，传感器以一定角度旋转时，重力加速度g在x′轴上的投影Ax等于加速度计测得的x′向加速度，如式(5)和式(6)所示：

图1 双轴的传感器转角Fig.1 Double axis sensor corner

式中：Ax为重力加速度在x′轴上的投影；θ为倾斜角。

当传感器的分辨率不高时，单轴传感器倾斜可能提供不准确的读数，所需最低分辨率由式(7)确定：

式中：R为该方法测量倾斜角所需的最小分辨率；N为倾斜角测量范围；P为测量角度的最小极限值。加速度计的灵敏度限制了该方法的检定精度。为了保持一个可靠的准确性，N、P、R应该满足特定的要求。

为了进一步提高测量精度，研究人员额外集成了一个传感器来测量重力加速度g在y′轴上的投影，如图1所示。同理，重力加速度g在y′轴上的投影Ay等于加速度计测得的y′向加速度，如式 (8) 所示：

式中，Ay为重力加速度在y′轴上的投影。

通过合成式(5)和式(8)计算Ax和Ay之间的比值，可以确定倾斜角的正切值：

在式(10)的两侧取反正切函数，可得所测结构的倾斜角，如式(11)所示。

两轴测量方法降低了传感器灵敏度影响，消除单个传感器可能存在的误差。通过融合x轴和y轴上的加速度数据，可以检定出更精确的倾角。

伪静态横向偏转响应一般在0 Hz～0.5 Hz[22]。因此，通过简单动态平均(SMA)滤波器衰减动态分量获得伪静态倾斜角，如下所示：

式中： θt为包含动态和伪静态分量的总倾斜角；i、j为测量加速度的第i、j个时间步；n为测量数据平均窗口内的点数(即平均窗口的大小)。

假设作用于墩顶的荷载P产生伪静力位移为Δp，根据欧拉-伯努利梁理论，桥墩墩顶位移 Δp可以表示为，如下：

式中： Δp为检定的伪静态位移； θp为伪静态倾斜角；P为作用在桩端的力；L为桥墩的简化模型高度，一般取桥墩高度的4/3倍；E为桥墩的弹性模量；I为桥墩截面惯性矩。

然而，桥墩桩土之间并不是固结的，通常是无位移有转角的，特别是基础受如水流冲刷等作用影响时。因此，本文考虑基础条件，通过在墩底增加两个传感器来提高位移检定精度。

式(13)需要被重新定义，根据欧拉-伯努利梁理论，可以得出 Δp：

式中：L1为桥墩墩高；L2为桩基础高度；E为桥墩的弹性模量； θ1为墩顶伪静态倾斜角； θ2为墩底伪静态倾斜角；P为作用墩顶的荷载；I为桥墩截面惯性矩。本文采用的结构计算原理简图如图2所示。

图2 结构简图Fig.2 Structure calculation principle sketch

结合式(17)和式(18)可得：

将式(19)代入式(16)可得 Δp：

由式(20)可以看出，低频伪静态位移与桥墩的地基条件、外荷载无关，并且可以通过墩顶、墩底的转角数据与桥墩墩高计算：

1.4 总检定位移

叠加这两条动态检定位移时程曲线与伪静态位移时程曲线以获得最终的总检定位移时程曲线。无参考位移检定法的整体流程图，如图3所示。

图3 总位移检定图Fig.3 Total displacement estimation

式中： Δt为总检定位移； Δd为动态检定位移；Δp为伪静态检定位移。

2 振动台试验

2.1 试验设备

该试验的主要目的是收集实时加速度和位移数据，因此传感器设备对位移检定精度影响较大。主要的测量传感器分为电容式加速度计和线性可变差动变压器(LVDT)，如图4和图5所示。电容式加速度计负责收集加速度数据，LVDT负责收集位移数据。加速度计信号和参数如表1所示，LVDT参数如表2所示。

图4 Model3711E1110G直流响应加速度计Fig.4 Model3711E1110G DC responsive accelerometer

图5 线性可变差动变压器(LVDT)Fig.5 Linear variable differential transformer

表1 Model 3711E1110G直流加速度计性能参数Table 1 Model 3711E1110G DC accelerometer performance parameters

表2 线性可变差动变压器(LVDT)性能参数Table 2 Linear variable differential transformer (LVDT)performance parameters

2.2 试验设置

试验所选用的桥墩模型与单自由度试验一致，采用长44.7 cm、宽14.8 cm、厚0.8 cm的板，其弹性模量为0.92 GPa、刚度为104.7548 N/m。实验设置如图6所示，实验模型模拟一个倒置的桥墩，模型顶端为约束端，实验通过2个固定在固定支架上的L型钢片约束模型，约束并不对称，用来模拟土对桥墩的约束并释放模型顶端的转动自由度 θ2，如图6(b)所示。模型底端为自由端，底端伸入两个固定在振动台上的L型钢片之间，并与振动台之间留有一定的空间。振动台上固定的两个L型钢片与模型之间留有一定的空间，空间内填充阻尼垫用以传导振动台对模型的横向位移激励的同时减少多余振动，如图6(c)所示。加速度传感器放置在悬臂板底部和顶部，以收集实时加速度数据a¯ 和 转角数据 θ1和 θ2，如图6(a)和图6(c)所示。位移传感器放置在悬臂板底部，以收集实时位移数据，如图6(d)所示。结构简图见图2(c)。

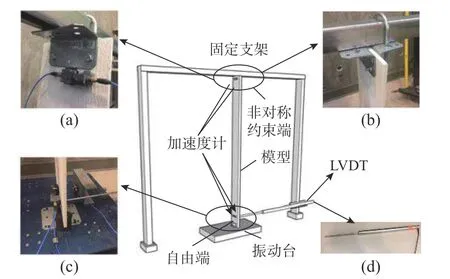
图6 试验整体设置Fig.6 Overall experimental setup

2.3 位移输入

本文试验中输入振动台的位移数据是实际在役铁路桥在列车从南北两个方向通过桥梁期间测得的。本研究团队选取了10组位移时程数据。考虑到振动台振动范围有限，在输入位移时程数据时，位移峰值不得超过振动台的限制，如果位移峰值超过振动台位移限制，则将整个输入的位移时程数据乘以一个系数。振动台按位移时程输入数据对模型底端产生横向的激励。输入10组列车位移时程数据如表3所示。

10组位移时程数据如表3所示。第1组和第2组位移时程数据都大于70 s，属于长时程；第3组～第7组位移时程数据在20 s～40 s，属于中等时程；第8组～第10组位移时程数据小于20 s，属于短时程。除了在持续时间上的不同，振幅也存在一定的差异。第1组和第2组长位移时程数据的峰值约为6 mm，第3组～第7组中位移时程数据峰值在6 mm～10 mm，其中，第6组时程数据峰值为11.41 mm，第8组～第10组短位移时程数据峰值超过阈值(10 mm)。为了更好地比较分析，在图7中，研究人员在相同的坐标轴上放置了4组位移时程曲线，其中包括1组长期、2组中期和1组短期。

图7 激励位移时程曲线对比Fig.7 Comparison of excitation displacement time history curves

表3 10组位移时程数据Table 3 10 sets of displacement time history data

3 实验结果和分析

3.1 试验结果和分析

将LVDT测量的实际位移时程曲线定义为参考位移，运用SMA滤波器衰减参考位移中动态位移时程曲线得出参考伪静态位移时程曲线，再使其与基于加速度传感器测量数据检定得出的伪静态检定位移时程曲线进行对比。将LVDT所测量的参考位移时程曲线减去用SMA滤波器得出的参考伪静态位移时程曲线，可得参考动态位移时程曲线，再使其与基于加速度传感器测量数据检定得出的动态检定位移时程曲线进行对比，如图8所示。图8(a)、图8(b)和图8(c)分别为三组位移指的是总位移中的检定位移与参考位移、动态位移中的检定位移与参考位移和伪静态位移中的检定位移与参考位移

在三组位移对比中，动态位移曲线的拟合较好。伪静态位移在低速下也能很好地拟合，但在中高速下对部分波段的峰值位移的拟合出现了误差，这可能与传感器采集数据的频率有关。其中部分数据段尾部不能归零，这是由于传感器采集的数据噪声引起的。因此在总位移的对比中，有部分数据段尾部有明显的数据不归零现象。但就整体而言，基于加速度传感器的检定位移，无论在结构的峰值位移还是整体位移，其拟合效果都更加令人满意。

为了更加量化地比较，以研究基于加速度传感器位移检定法的性能，研究人员使用2个参数来量化位移检定的准确性。第一个参数E1确定了检定位移和实际位移之间的峰值误差，第二个参数E2确定了检定位移和实际位移之间的均方根RMS误差。性能参数越小表示性能越好。峰值位移误差E1和均方根RMS位移误差E2公式如下：

式中： |i|为i的 绝对值；RMS(i) 为i的 均方根；Δest为检定位移时程曲线； Δref为参考位移时程曲线。

对三组对比曲线分别进行误差计算，可得动态位移时程曲线、静态位移时程曲线以及总位移时程曲线的两种误差的量化值，如表4和表5所示。

表4和表5记录的试验结果表明，10次试验结果中，就峰值位移检定误差而言，本文所提出的基于加速度传感器检定总位移峰值位移误差E1最大值为11.80%，最小值为0.08%，平均值为5.45%，峰值位移检定性能有波动，但平均误差较小。在均方根位移对比中，检定总位移均方根误差E2最大为8.05%，最小值为3.61%，平均值为5.47%，整体位移检定性能稳定，误差较小。综上所述，基于加速度传感器的位移检定法，无论在峰值位移的检定上还是在均值位移的检定上，都具有很好的位移检定精度。

表4 10组检定位移时程曲线峰值位移误差E1数据Table 4 Peak displacement error E1 of 10 sets of estimated displacement time history curves

表5 10组检定位移时程曲线均方根位移误差E2数据Table 5 RMS displacement error E2 of 10 group estimated displacement time-course curve

4 结论

本文讨论了一种基于加速度传感器的新的位移检定方法的试验验证，该方法利用无参考电容式加速度计传感器检定铁路桥梁的总横向位移。直流加速度传感器能够稳定持续的监测结构，采集结构响应。其外壳坚固能确保在低劣的环境中应用。加速度传感器有着广泛的监测频率范围，确保数据采集的完整性和低噪声。为了验证所提出的方法，研究人员采用10组实测铁路横向移位作为振动台的输入对试件进行激励。读取放置在试件上的电容式加速度计数据，近而估算试件位移并与LVDT测得的参考位移进行比较评估量化参数下的位移检定精度。

(1) 本文所讨论的新方法基于加速度传感器来检定铁路轻型桥墩的横向位移，该方法能够克服现有的位移监测法的局限性，具有无需固定参考点、不受天气条件限制、低成本、易操作、长期稳定、误差小等优点。

(2) 直流加速度传感器能够稳定持续的监测结构，采集结构响应。其外壳坚固能确保在低劣的环境中应用。加速度传感器有着广泛的监测频率范围，确保数据采集的完整性和低噪声。

(3) 就总位移检定而言，在本文所提出的量化评估标准下，整体位移检定性能稳定、误差较小，峰值位移检定性能有波动，但平均误差较小，位移检定准确度较好。基于加速度传感器的位移检定法可以作为一种替代传统位移传感器监测结构位移的方法。