融合狼群算法和模糊聚类的混合推荐算法

王永贵，李 昕

辽宁工程技术大学 软件学院，辽宁 葫芦岛 125105

随着数字时代的到来和大数据的发展，互联网用户群体不断扩大，从海量的数据信息中精准地找到所需内容越来越困难。推荐系统应运而生，帮助用户筛选出有效信息，实现个性化推荐。协同过滤算法是在推荐系统中普遍应用且较为成熟的推荐算法，也是推荐系统中的热门研究内容。许多超大型电子商务网站都使用了协同过滤算法，比如淘宝网、京东商城、当当网等；随着信息时代的快速发展，用户数量急剧增加的同时伴随着庞大的信息量，造成数据的稀疏性，从而降低了算法的推荐准确率，影响推荐效果。

传统的协同过滤推荐算法主要包括基于用户的协同过滤算法和基于项目的协同过滤算法，旨在寻找用户以往在网站中的活动信息，剔除无关信息，挑选出有价值的内容或者商品推荐给用户。由此可见，寻找目标用户和推荐内容的潜在关系是推荐的关键。随着推荐系统的壮大和成熟，众多研究专家结合推荐系统和数据挖掘中的聚类模型，借助聚类算法的优势解决推荐系统中存在的问题。古话讲：“物以类聚，人以群分”，聚类的目的就是按照一定的划分标准对人或物进行分类。因此将聚类模型运用到推荐系统中，深度挖掘用户和用户、用户和物品以及物品和物品的关系，在很大程度上提高了推荐效率和推荐质量。同时，协同过滤算法中普遍存在海量的数据信息，依靠聚类算法较高的伸缩性可以降低其时间复杂度。

为降低数据稀疏程度、提高推荐准确率，许多研究者对传统的协同过滤算法进行了改进。魏甜甜等人[1]考虑到项目流行度差异，引入惩罚权重函数加入到传统的协同过滤算法中。张瑞典[2]根据项目在当前市场上热度大小设置不同的权重值，综合考虑用户偏好程度构建用户相似度矩阵。充分考虑影响评分相似度计算的因素并加以改进，提高了算法效率，但是忽略了数据稀疏性太大对算法执行率的影响。黄贤英等人[3]研究用户的兴趣爱好，对体现用户对项目喜好程度的矩阵使用K-means算法进行聚类，提高了推荐准确率。刘国丽等人[4]在传统聚类推荐算法中融入专家信任值以改进预测评分的计算。李瑞等人[5]将K-means聚类算法与SVD++模型融合后加入到传统算法中，使用SVD++模型对聚类后的用户-项目评分矩阵分解，解决了数据稀疏性的问题。但是K-means算法属于硬聚类算法，只能按照聚类标准将数据严格划分到一个类别中，但是在现实的推荐系统中，用户或者项目均有多个标签分别属于不同类别。因此针对K-means聚类算法应用在推荐系统中存在的问题，Gong等人[6]构建模糊相似度矩阵，利用模糊聚类算法形成最近邻居集合。Kumar等人[7]结合模糊C-均值聚类算法到传统的协同过滤推荐算法中，可以根据用户评分相似性聚类到不同的类别中。胡朝举等人[8]提出一种基于用户模糊聚类的个性化推荐研究，使用模糊聚类算法以提高聚类的正确率。上述模糊聚类算法的提出均有效提高了推荐准确率，但是忽略了数据稀疏性对聚类算法的影响，也忽视了随机生成的初始聚类中心对推荐效果所产生的影响。

针对上述研究成果中存在的问题，同时基于狼群算法可以快速地找到最优解，有效减少模糊聚类随机初始聚类中心对聚类结果的影响。提出融合狼群算法和模糊聚类的混合推荐算法。首先利用基于项目的协同过滤算法生成预测评分填充原始数据中的零值，主要根据目标用户对未评分项目相似项目集合的评分进行预测。然后使用狼群算法优化的聚类算法对用户进行模糊聚类，根据对类簇的隶属度大小选择最近邻居集合，按照计算得到的预测评分进行推荐。经实验表明，该算法具有更优的推荐性能，在解决数据稀疏问题的同时为目标用户提供高质量且多样化的推荐。

1 传统的协同过滤算法

在推荐系统中较为完善且应用成熟的传统算法主要包括基于用户的协同过滤和基于项目的协同过滤。推荐系统中有数以万计的用户量，但是仅有部分用户和项目之间存在评分关系，推荐算法根据当前的数据预测用户和项目评分关系中的空白信息，选择合理的项目推荐给用户。协同过滤主要包括三部分：对用户活动信息的获取；挑选邻居集合；预测评分，产生推荐[9]。

1.1 用户活动信息的获取

用户活动信息是用户在各大型网站中开始搜索、点赞、评分等操作，一直到停止搜索时产生的各种行为信息。在传统的协同过滤算法中，用户活动信息具体为用户对各项目的评分数据，表示为用户-项目评分矩阵Rm×n，如公式（1）所示：

其中，行数m表示用户集合U，列数表示项目集合I。rij表示用户对项目的评分大小，取值范围为0～5，0值表示用户未对项目进行打分，数字1～5是用户对项目的打分数据。评分大小在很大程度上体现出了用户对该项目的偏好喜爱程度。

1.2 挑选邻居集合

协同过滤算法中的邻居集合包括邻居用户集合和邻居项目集合，同一邻居集合中的用户或者项目间的相似度较高。挑选邻居集合的过程主要分为两个部分：计算相似度大小，选取最近邻居。

1.2.1 计算相似度大小

计算相似度大小是选择最近邻居的前提，是影响推荐效果的关键性因素。常用的计算相似度的方法有余弦相似度、皮尔逊相似度和修正的余弦相似度，通过把公式（1）中的数据转化为向量进行计算。不同用户间的评分标准不同，余弦相似度公式没有考虑用户评分尺度问题对计算结果的影响。皮尔逊相似度需要根据用户间的共同评分进行计算，不适用于稀疏性较大的数据集，而本文算法实验数据集的稀疏性均高于90%。故选择修正的余弦相似度公式进行计算，如公式（2）所示：

修正的余弦相似度公式改善了用户评分尺度问题对计算结果的影响，扩展性较好。其中，Ui∩Uj表示对项目i和项目j同时评分过的用户集合，rˉu表示用户对评分过的项目集合的平均评分。

1.2.2 选择最近邻居

对公式（2）求得的相似度大小降序排列，选择前K个用户或者项目作为最近邻居集合。

1.3 预测评分，产生推荐

在协同过滤推荐中，将目标用户的预测评分作为依据生成推荐列表，过滤已发生交互行为的项目进行推荐，形成推荐结果。预测评分是目标用户参考历史数据信息，对没有数据关系的项目计算得到的评分。

1.3.1 基于项目的推荐

在基于项目的协同过滤推荐算法中，充分挖掘项目间的潜在关系和深层关系，以寻找物品间的关联性。首先要找到目标用户未评分项目的相似项目，获取目标用户对相似项目的历史评分数据，最后使用权重求和法[9]计算预测评分。计算过程见公式（3）：

其中，ru,i表示用户u对项目i的评分，Ij表示项目j的邻居集合。

1.3.2 基于用户的推荐

在基于用户的协同过滤推荐算法中，将相似用户的评分数据作为依据，通过公式（4）对预测评分进行计算：

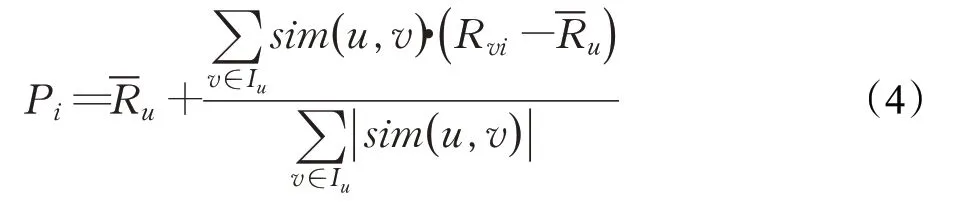
2 基于狼群算法和模糊聚类的协同过滤

传统的协同过滤推荐在数据稀疏的环境下，很难为目标用户找到可靠的相似用户，影响推荐结果。因而提出使用基于物品的协同过滤推荐面向稀疏矩阵，进行数据填充，以确保数据的完整性。然后使用狼群算法优化的模糊C-均值聚类算法加入到传统的协同过滤算法中，找到可靠的邻居用户，参考其历史数据形成推荐列表，过滤目标用户已经产生交互行为的项目后，形成最终的推荐列表。基于狼群算法和模糊聚类的协同过滤旨在降低实验数据集稀疏性的同时为用户提供高精度、高效率、高质量的个性化推荐内容，增强用户的体验感。此推荐系统的流程图如图1所示。

图1 融合狼群算法和模糊聚类的推荐系统流程图Fig.1 Flow chart of recommendation system integrating wolf colony algorithm and fuzzy clustering

2.1 基于项目的协同过滤算法填充数据矩阵

推荐算法中有难以数计的用户数量，数不胜数的物品数量，信息量十分庞大。但是产生交互行为的数据信息很少，只有少部分用户会有评分行为，有共同评分行为的数据更少，甚至没有。由于数据极具稀疏，可能会造成计算相似度时误差偏大，导致推荐结果产生偏差，推荐效果不好。

为解决上述问题，使用传统的基于项目的协同过滤推荐对数据矩阵进行填充。根据用户对项目的评分，结合项目相似度计算公式，找到与未评分项目相似度最高的K个物品。基于相似物品的历史评分记录，计算目标用户对未评分项目的预测评分替换原始矩阵的零值。物品相似度更能体现它们之间的潜在关系和深层关系，从物品角度出发，更具有实际意义。预测公式见公式（3）。

2.2 狼群算法

狼群算法（WPA）是一种群体智能算法，将自然界中狼群的群体行为抽象地用数学公式表示出来。在自然界中，狼群处于食物链顶端的位置，等级制度划分严密。主要分为头狼、探狼、猛狼三种类型，它们分工明了又相互配合共同完成捕杀任务。探狼根据嗅到的猎物气味浓度判断是否向靠近猎物的方向运动，并将搜寻信息报告给头狼；头狼是狼群中的军师，接收反馈信息后，指挥猛狼朝向探狼的方向行动；猛狼在接收到命令后，开始捕杀行动。狼群算法模型[10]如图2所示。

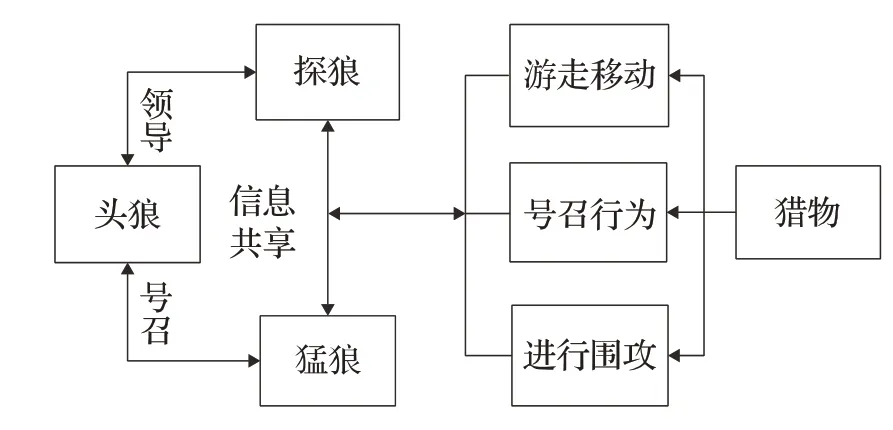
图2 狼群算法模型图Fig.2 Wolf colony algorithm model

狼群算法分为五个部分：算法初始化、游走活动、号召行为、进行围攻、狼群更新。

（1）算法初始化

狼群的活动范围是一个N×D的活动空间，D是寻优变量数量，N是狼的数量。狼群中某一只人工狼的位置Xi=( )xi1,xi2,…,xiD,i=1,2,…,N，目标函数值为Yi=f()X，为人工狼感知到的猎物气味浓度。选择目标函数值最大的狼为头狼，设为Ylead。

（2）游走活动

目标函数值较优的一部分狼群为探狼，它们分别朝h个方向游走，移动到新的位置搜寻猎物，计算当前位置的目标函数值后返回并且重新出发，不断重复这个过程，最终选择目标函数值最大的位置前进。当Yi＞Ylead时，或者游走次数达到上限后，更新位置。探狼游走活动由公式（5）表示：

其中，表示探狼向第p个方向前进后的位置，p=1,2,…,h。Xi是探狼出发时的位置，stepa是探狼的活动步长。

（3）号召行为

猛狼以头狼的位置为目标进行奔走，负责食物的供给且听从头狼的召唤。在这个过程中，如果猛狼的目标函数值大于头狼的目标函数值，则代替头狼的位置和职责。当两者距离小于阈值时，算法进行到下一步。猛狼的位置变化可由公式（6）表示：

（4）进行围攻

奔袭的猛狼向猎物靠近时，联合以猎物为目标进行游走的探狼发起围攻。此时，将头狼的位置视为猎物的位置，围攻行为由公式（7）所示：

（5）狼群更新

狼群算法模仿达尔文的自然选择学说对狼群进行优胜劣汰，并且执行按劳分配猎物的原则。捕猎过程中贡献较大的狼优先分配猎物，一些弱小且未能参与到捕猎过程中的狼可能会因为没有分得猎物而饿死，从而在狼群中去除适应度值最差的R匹狼的同时，随机产生R匹狼补充到队伍中，更新狼群，实现狼群的多样化。

2.3 模糊C-均值聚类算法

使用传统的聚类算法后，每个项目只能被划分到一个类别中，在许多大型网站中应用受限。而模糊聚类的聚类结果更加灵活，根据不同的隶属度将一个项目划分到不同的类别中，弥补传统聚类算法的缺陷，其中被广泛应用的是模糊C-均值聚类算法（FCM）。

将FCM聚类算法加入到评分矩阵Rm×n，根据所有用户对物品的评分信息模糊聚类，将用户集合X划分到c个类簇中，在同一个类簇中的用户相似度最高。聚类中心C={C1,C2,…,CC}，用户对聚类中心的隶属度为μij。为了得到更好的聚类结果，将约束条件设置为聚类结果是用户隶属度矩阵U=(μij)n×c。聚类的过程是使目标函数值达到最小的过程，目标函数可以表示为公式（9）：

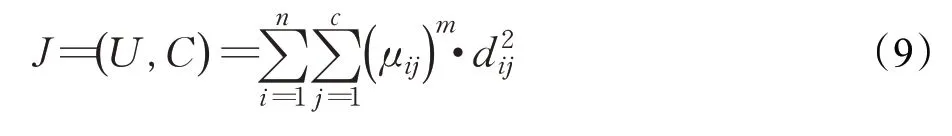
其中，m是刻画模糊程度的参数，最佳选择范围是[1 ,2.5]，一般取为2。μij可表示为公式（10），即用户i属于第j个簇的隶属程度；Cj为用户簇j的聚类中心，如公式（11）所示；公式（12）中dij是各用户和聚类中心之间的距离。

其中，用户和聚类中心的距离为模糊聚类的主要依据。根据距离的大小计算隶属度后进行比较，将用户按照隶属度的大小进行分类，尽可能地使得同一簇中用户的相似度最高，不同簇中用户的相似度低。

预测评分时，同一个簇中的相似用户对目标用户的影响不同。引入距离公式作为一个权重到评分预测公式中，以消除上述影响。

2.4 狼群优化的模糊C-均值聚类算法

聚类中心位置的选取影响着聚类效果，如果设置不合理，则限制算法的收敛性[11]，使算法容易陷入局部最优或者很难找到全局最优。FCM算法初始聚类中心位置的随机性决定算法的性能。而狼群算法的收敛速度很快，对参数的敏感性比较低，求解质量较高[10]。因而提出狼群优化的模糊C-均值聚类算法（WPA-FCM），获取合理的聚类中心。

算法思想：利用狼群算法找到初始聚类中心，根据得到的聚类中心使用FCM算法对用户进行聚类。此算法适应度函数设置为fitness=J。

算法流程：

输入：用户-项目评分矩阵、用户聚类个数、狼群大小N、狼群进化迭代上限kmax、狼群进化占比R、探狼在狼群中的占比α、探狼游走上限Tmax、聚类停止迭代的阈值ε。

输出：用户簇隶属度矩阵U。

步骤1根据公式（9）计算狼群的适应度大小，选择适应度最大的为头狼，并且划分出探狼和猛狼。

步骤2探狼进行全局搜索，计算探狼当前的适应度值，并且和头狼进行比较。fi＞flead时或者活动次数达到游走上限Tmax时，停止活动。

步骤3按照公式（5）计算探狼的位置并更新。

步骤4猛狼以头狼的位置为目标进行搜索，将其适应度值和头狼进行比较。fi＞flead时，猛狼代替头狼的位置；fi＜flead时，猛狼继续搜索，一直到猛狼和头狼之间的距离小于阈值d。

步骤5在狼群进行围攻行为之后，根据公式（5）～（7）对各狼的位置进行更新，将距离猎物最近的人工狼的位置视为新的头狼位置。

步骤6根据狼群进化占比R更新狼群。

步骤7判断狼群算法是否停止：如果k＜kmax，继续迭代过程，k=k+1，算法跳回步骤1，继续优化过程；k＞kmax时，算法终止，输出最优值。

步骤8根据最优值初始化FCM算法的聚类中心，初始化用户隶属度矩阵U。

步骤9根据公式（10）、（11）计算、更新聚类中心矩阵C和隶属度矩阵U。

步骤10计算目标函数值并进行比较，J(T)-J(T+1)＜ε时，停止迭代，输出用户簇隶属度矩阵U；否则，返回步骤9继续迭代过程。

2.5 推荐过程

本文提出基于狼群算法和模糊聚类的混合推荐算法，首先获取历史数据对数据矩阵进行填充；其次，通过狼群算法优化的模糊C-均值聚类算法对用户分类；最后，使用协同过滤进行推荐。推荐过程如图3所示。

图3 推荐过程Fig.3 Recommendation process

3 实验与分析

3.1 数据集的选择

MovieLens 100K数据集中有943名用户对1 682部电影的评价数据。MovieLens 1M数据集中有6 040名用户对3 952部电影的评价信息。两个数据集中均包含了用户的基本信息、电影的属性信息以及用户对电影的评分数据。用户对电影的评价数据量数以万计，并且分为5个不同的等级（1分～5分），分数越高代表用户对电影的评价越高，但是数据的稀疏性分别高达约94%、96%。

预处理数据集，提取出用户的评价数据和电影的属性信息，构建用户-项目评分矩阵；同时划分数据集，将数据集的80%作为训练集，数据集的20%作为测试集，数据集之间相互独立，涵盖了全部数据。

3.2 评价指标

实验采用平均绝对误差（MAE）、均方根误差（RMSE）作为评价算法推荐质量的指标，根据用户实际评分和预测评分之间的偏差评估推荐准确率。计算结果越小，误差越小，表明算法的推荐质量越高。

其中，pu,i代表目标用户对电影的预测评分，ru,i代表目标用户的实际评分，n是数据集中已有评分的电影数量。

3.3 实验结果与分析

实验1为验证填充后的用户-项目评分矩阵优于原始的用户-项目评分矩阵，将基于数据填充的混合协同过滤（hybrid）、基于项目的协同过滤推荐算法[12]（ItemCF）、基于用户的协同过滤[13]（UserCF）在数据集MovieLens 100K上进行对比实验，在最近邻居数目分别取20、30、40、50、60的时候，比较MAE的值，实验结果如图4和图5所示。

图4 UserCF、ItemCF、hybrid算法的MAE变化Fig.4 MAE changes of UserCF，ItemCF，hybrid algorithm

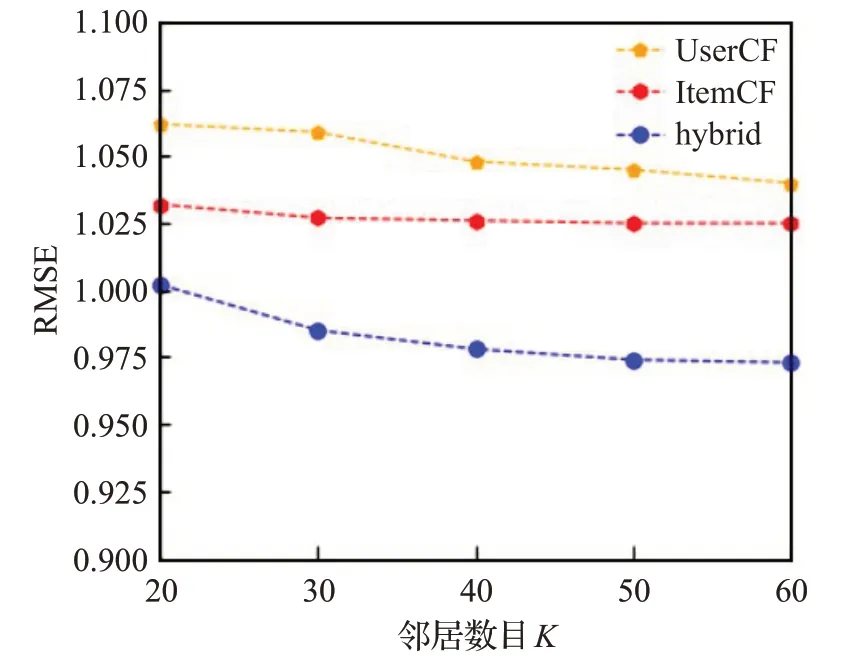
图5 UserCF、ItemCF、hybrid算法的RMSE变化Fig.5 MAE changes of UserCF，ItemCF，hybrid algorithm

经实验结果表明，基于数据填充的混合协同过滤的MAE值在0.80附近上下波动，较UserCF的MAE值降低了5%，比ItemCF的MAE值降低了3%，充分说明填充数据矩阵后进行协同过滤推荐，推荐效果更好，在缓解数据稀疏性的同时为用户提供高质量的推荐内容。

从图5中可以看出，hybrid算法的RMSE值均低于UserCF算法、ItemCF算法的值，可见hybrid算法的有效性。在缓解数据稀疏性的同时，推荐结果具有更高的精度。在同等数据条件下，hybrid算法优于传统的协同过滤算法。

实验2设置WPA-FCM算法参数：探狼比例因子α=4，狼群进化的比例因子R=6，狼群进化迭代上限kmax=300，探狼游走上限Tmax=30，聚类停止迭代的阈值ε=0.01。

为了研究聚类个数与实验结果的关系，在聚类结果分别取10、20、30、40、50、60的情况下进行实验，其MAE、RMSE结果如图6、图7所示。

图6 MAE随聚类个数的变化情况Fig.6 Change of MAE with number of clusters

通过图6、图7实验结果可知，不同的聚类个数直接影响了推荐准确度的高低。随着聚类个数C的增加，MAE、RMSE的值也在不断增加，误差逐渐增加，即推荐效果逐渐减弱。根据实验结果，选择聚类个数为10的时候推荐效果最佳。

图7 RMSE随聚类个数的变化情况Fig.7 Change of RMSE with number of clusters

实验3 WPA-FCM算法与其他协同过滤算法分别在不同的数据集上进行对比实验，以验证WPA-FCM算法的适用性和有效性。选取基于用户模糊相似度的协同过滤算法[8]（UserCF-FCM）、基于项目模糊相似度的协同过滤推荐算法[14]（ItemCF-FCM）在MovieLens 1M数据集上进行对比实验，如图8；选取UserCF[13]、K-Means算法[15]、Kmeans-SVD算法[5]、FCM算法[6]在MovieLens 100K数据集对比实验，如图9。聚类个数为10，最近邻居个数分别选取20、30、40、50、60。

图8 Movielens 1M算法对比Fig.8 MovieLens 1M comparison of algorithms

如图8，当邻居数量从20变化到60的时候，三个算法的MAE值均不断减小，且趋于平稳。在Movielens数据集中，WPA-FCM模糊用户评分信息，寻找用户与电影间的关系，算法精度始终高于UserCF-FCM、ItemCFFCM。WPA-FCM算法适用于数据稀疏且用户关系模糊的数据集。

根据图9可以看出，与其他4种算法相比，本文提出算法的MAE值最小，推荐效果更好。K-Means算法、Kmeans-SVD算法分别在UserCF算法上融合了硬聚类的方法，在电影推荐系统中应用受限，推荐精度低；FCM算法在UserCF算法上融合了软聚类算法，增强推荐系统的推荐效果，但是算法随机初始聚类中心的选取对实验结果影响较大。以上算法均未考虑到数据稀疏对聚类结果的影响，本文算法在缓解数据矩阵稀疏性的同时，加入狼群优化的模糊C-均值聚类算法，降低随机的初始聚类中心对聚类结果的影响，同时提升了聚类效果，在候选邻居簇中选取最近邻居，提升选取邻居的精确度，大大提高了推荐系统的推荐质量。

4 结束语

由于传统的基于用户的协同过滤算法数据稀疏程度高，推荐准确度低，本文提出一种基于狼群算法和模糊聚类的混合推荐算法。为了降低数据稀疏性，利用基于项目的协同过滤算法预测目标用户对电影的评分，充分挖掘电影之间的潜在关系，将预测评分填充到原始的用户-项目评分矩阵。为了增强推荐效果，提高推荐质量，融合模糊C-均值聚类算法到传统算法中，根据隶属度的高低将用户分为不同的类别；同时加入狼群算法优化聚类算法的初始聚类中心，增强聚类效果。实验表明，本文提出算法有效解决了以上问题，提高了个性化推荐的质量。今后将研究重点放在时间因素对用户兴趣的影响，以提高推荐精度。