基于随机森林回归算法的锅炉沾污因数预测方法
谢 春 许 伟
上海电气集团股份有限公司 中央研究院 上海 200070
1 研究背景
锅炉是能源行业的关键设备,运行状态会影响整个系统的工作效率。锅炉的积灰污染是影响锅炉正常运转的一个非常重要的因素。
沾污因数是定量表征锅炉积灰污染程度的指标,沾污因数的大小可以直观有效指导工作人员对受热面进行吹扫,保障锅炉安全运行。当前,主要基于操作人员的经验,结合锅炉受热面的温度、蒸汽压力等监测数据及锅炉的负荷较为粗略地评估锅炉的积灰程度。
用沾污因数表征锅炉积灰污染程度是较为科学和直观的方法,但是存在不足。
积灰污染是一个相当复杂的物理化学过程,积灰污染的机理尚不明确,有关积灰过程的理论研究与试验十分欠缺,沾污因数的计算存在公式模糊、计算困难的问题。另一方面,基于人工经验的评估方法没有考虑沾污因数随时间周期性变化的特征,并且没有充分利用历史数据,结果不能准确地描述锅炉的积灰程度[1-3]。
随着计算机技术的发展,基于机器学习对锅炉沾污因数进行预测成为一个可行的研究方向。随机森林回归算法可以量化复杂的非线性关系,预测结果不受异常值和冗余数据的影响,并且不会产生明显的过拟合风险[4]。鉴于此,笔者充分考虑锅炉运行的周期性,对锅炉历史监测数据进行特征重构,以重构特征作为输入数据,通过超参数搜索,建立基于随机森林回归算法的锅炉沾污因数预测模型,实现对锅炉沾污因数的预测,同时对模型的预测性能进行评价。
2 随机森林回归算法
随机森林回归算法是一种集成学习算法,聚合多棵分类树,每棵分类树由独立采样的随机向量赋值。随机森林回归算法利用自展重抽样方法,从原始样本中抽取多个样本,对每个样本进行决策树建模,组合多棵决策树的预测,通过投票得出最终预测结果[5-6]。
随机森林回归算法流程如图1所示。

图1 随机森林回归算法流程
随机森林回归模型采用均方根误差、拟合优度两个评价指标。均方根误差可以反映样本的离散程度,值越小说明精度越高,值的大小受预测数值的大小影响。拟合优度可以检验随机森林回归模型对样本数据的拟合程度,取值在0~1之间,值越高表示模型的可解释程度越高[7]。
均方根误差r为:
(1)
式中:N为样本总数;n为样本序号;Y′n为第n个样本预测值;Yn为第n个样本标签值。
拟合优度R2为:
(2)

3 案例分析
选择某电厂2020年3月~5月的锅炉历史数据作为试验数据,由安装在锅炉特定受热面上的传感器获得。锅炉历史数据采集频率为每15 min采集一次,包括锅炉负荷W、指定受热面温度T、蒸汽压力P,以及根据既往统计和传统经验得到的沾污因数,该沾污因数经过技术人员调整,可以认为是较为准确的标签数据。
3.1 特征重构
在充分考虑锅炉运行周期性,突显历史数据变化趋势的基础上进行特征重构,以便通过随机森林回归算法获得更好的预测结果。

(3)
(4)

对各特征数据按照式(3)和式(4)进行特征重构,将沾污因数作为标签数据,特征重构后的部分数据见表1。
3.2 模型训练与预测
采用随机森林回归算法对特征数据进行建模,随机森林回归模型有两个非常重要的超参数。一个是最大特征数,即一棵决策树最多有多少个特征变量,根据经验,每棵决策树输入约1/3的特征集。另一个是决策树数量[8-10]。为了确定最优的决策树数量,可以训练多个随机森林回归模型,每个随机森林回归模型的决策树数量由0至1 000等值增加。拟合优度随决策树数量的变化如图2所示。由图2可以看出,决策树数量大于100时,拟合优度已基本趋于稳定,因此可以将决策树数量设置为100来训练随机森林回归模型。
作为对比,在超参数设置相同的情况下,分别以未重构特征和重构特征来训练随机森林回归模型。未重构特征为负荷、蒸汽压力、温度,重构特征为蒸汽压力变化趋势指标、温度变化趋势指标。预测结果对比如图3所示。
由图3可知,基于重构特征训练得到的随机森林回归模型对锅炉沾污因数的拟合更好,解释性强,可以有效表征锅炉沾污因数的变化趋势。

表1 特征重构后部分数据
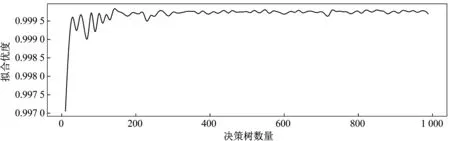
图2 拟合优度随决策树数量变化关系
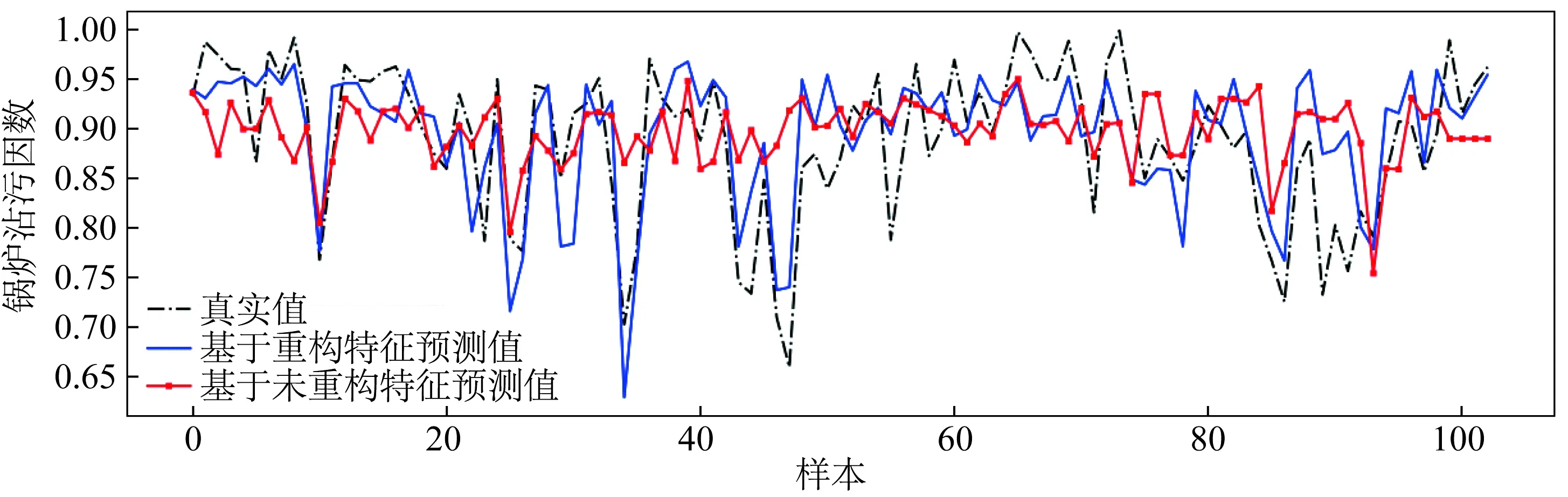
图3 预测结果对比
3.3 模型评估
利用式(1)、式(2)可以计算出基于未重构特征和基于重构特征的随机森林回归模型的均方根误差和拟合优度,见表2。
由表2评价指标可以看出,对数据进行重构后用于随机森林回归模型预测锅炉沾污因数,拟合优度达到0.764 2,明显优于未重构特征预测结果,可见重构特征可以有效显示锅炉状态数据与积灰程度之间的潜在规律,使随机森林回归模型能够更好地应用于锅炉沾污因数预测。
4 结束语
笔者通过研究提出基于随机森林回归算法的锅炉沾污因数预测方法。为充分体现锅炉运行的周期性特征,对历史数据进行特征重构,获得蒸汽压力变化趋势指标和温度变化趋势指标。以这两者作为训练特征,基于随机森林回归模型实现对锅炉沾污因数的预测。通过案例表明,这一方法可以很好地挖掘锅炉历史监测状态数据和锅炉沾污因数之间的潜在规律。在锅炉积灰机理尚不明确的情况下,应用这一方法预测得到的锅炉沾污因数具有一定的可靠性和参考性。

表2 随机森林回归模型评价指标

