基于遗传算法的长距离供水工程渠道应急决策方法

赵多明

(新疆额尔齐斯河流域开发工程建设管理局，新疆 乌鲁木齐 830000)

水资源是维持生产与发展的基础，因此现阶段社会对水资源的依赖性越来越高。然而，受到地形、气候以及人口等多重因素的影响，水资源并不平衡，导致部分地区或者城市无法满足供水需求[1]。面对这种情况，供水工程成为了一项重要的民生工程。通过供水工程能够将水资源丰富地区的水调度到水资源贫乏地区，以缓解当地水资源不足的问题[2]。在此背景下，水资源调度面临一个较大难题，即如何设计调度方案，尤其是面临突发用水事件时，由于考虑的因素的众多，制定合理的供水工程渠道应急决策方案变得更加困难，因此供水工程渠道合理调度成为当下研究的重点。

针对上述问题，很多已经发表的研究都给出了相应的解决方案。例如，吉瑞博等人考虑3种可靠性目标，设计了一种多目标优化模型，然后在水力平衡条件、节点服务水头需求以及流速限制等多种约束条件限制下，利用NSGA- Ⅱ算法求取最优解，得出供水决策方案[3]。曹明霖等人对多水源水库群系统进行多情景优化调度研究，在该项研究中将总缺水率和调水成本最小为目标函数，在水量平衡、库容、调水能力等条件约束下，求解了3种情景下的联合供水方案[4]。苏炯恒等人综合考虑到管网总成本、管网弹性力指数和水质3个目标，在满足多种条件下，利用自适应多目标进化算法求解最优管网设计优化调度方案[5]。

综合前人研究经验，针对长距离供水工程渠道，本文设计一种基于遗传算法的长距离供水工程渠道应急决策方法，以期为供水调度方案设计提供参考，提高应急决策能力。

1 基于遗传算法的长距离供水工程渠道应急决策方法

为缓解水资源短缺问题，满足生产、生活供水需要，供水工程的修建必不可少。供水工程能将水资源丰富地区的水资源调度到短缺的地区，以缓解水资源短缺的问题。正常情况下，用1～2条供水工程渠道就可满足调度需求，但是一旦遇到突发状况，如火灾，就需要多条供水工程渠道同时运作，以应对紧急需水情况，但是多条供水工程渠道如何科学调配以及协同运行成为难题[6]。针对上述问题，研究一种基于遗传算法的长距离供水工程渠道应急决策方法。在本研究当中，首先建立长距离供水工程渠道网络模型，然后建立多目标模型，接着设置约束条件，最后利用遗传算法进行求解，得出最优应急决策方案[7]。

1.1 长距离供水工程渠道网络建模

要想设计出合理的长距离供水工程渠道应急决策方案，明确供水渠道网络模型是前提和基础。供水渠道网络模型是实际供水管道的抽象简化模型，通过模型能够充分了解供水渠道分布情况，为后期建立目标模型，设置约束条件提供参考[8]。

借助WaterGEMS建模软件建立长距离供水工程渠道网络模型，建立过程如图1所示。

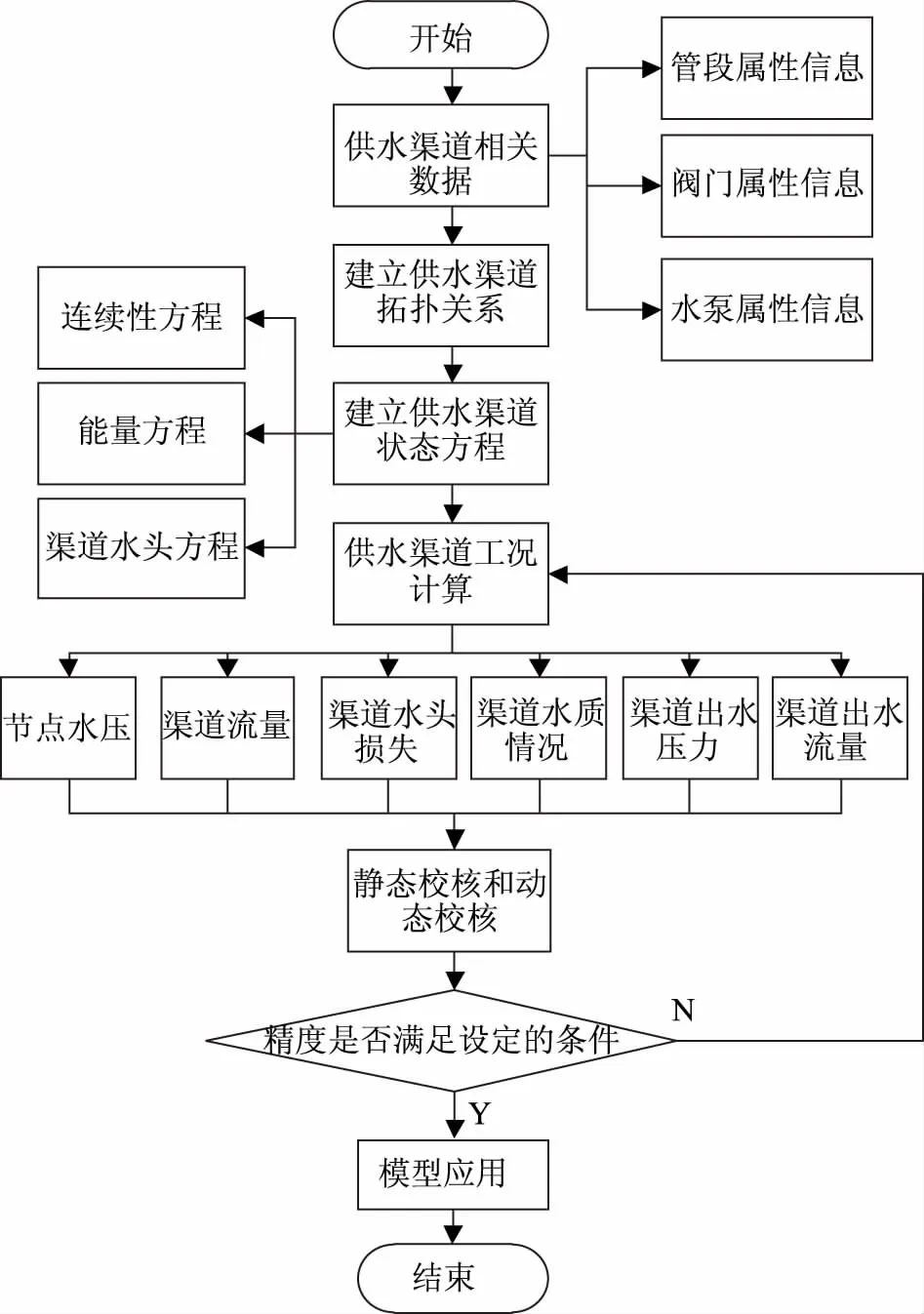
图1 基于WaterGEMS的长距离供水工程渠道网络模型

1.2 目标模型建立

由于是设计长距离供水工程渠道应急决策，而应急情况下的决策与一般情况的决策是不同的，一般情况下的供水决策方案多数都是以最小成本为目标的，而应急情况下的决策方法则不同，最小成本并不是第一考虑的目标，第一目标是最大出水量[9]。根据上述情况，将成本与出水量都作为目标，以此建立综合多目标函数模型。建立的多目标函数模型如下：

式中，Y1—最大出水量；Y2—最小成本；t—供水工程渠道运行时间；Ai—第i段供水工程渠道的供水流量；Li—供水工程渠道的长度；f—第i段供水工程渠道的运行成本函数；Bi—第i段供水工程渠道的流速；Ci—第i段供水工程渠道的供水压力；Di—第i段供水工程渠道的运行的能耗成本；n—供水工程渠道数量；S—供水能量不均匀系数。

1.3 约束条件设置

约束条件是目标模型的限制条件。

(1)水量供需平衡约束

供水渠道提供的水量需要与应急区域需水量相等，若前者大于后者，会造成水资源浪费；若前者小于后者，否则水量不足，无法满足应急需求[10]。约束条件公式如下：

(2)

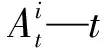
(2)供水渠道流速约束

供水渠道流速不能过快，否则容易管道事故；供水渠道流速过慢，否则不能满足应急要求[11]。针对这一点，需要进行供水渠道流速约束。约束条件公式如下：

(3)

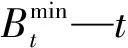
(3)供水能力约束

供水工程渠道的供水量每天都是有限的，不能超出设定的范围，由此设定供水工程渠道的供水能力约束条件[12]。约束条件公式如下：

(4)

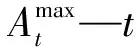
(4)运行水压约束

水在供水工程渠道中流动的时候会产生一定的水压，该水压不能超过最大值，否则会造成管道爆裂，水压不能过小，否则存在断流问题，由此设定供水工程渠道的水压约束条件[13]。约束条件公式如下：

(5)

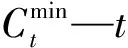
(5)数量约束

受到地形、成本、气候等因素的影响，并不是所有的供水工程渠道都能同时运行，因此设定供水工程渠道的数量约束条件[14]。约束条件公式如下：

(6)

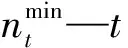
(6)非负约束

所有变量都不能是负数，因此设定非负约束条件。约束条件公式如下：

(7)

通过上述设置6个约束条件：水量供需平衡约束、供水渠道流速约束、供水能力约束、运行水压约束、数量约束、非负约束，利用这些条件为目标模型的解划定求解范围，方便后期求解。

1.4 基于遗传算法的供水工程渠道应急决策求解方案

在上述设置的6项约束条件后，利用遗传算法求解目标模型，得出供水工程渠道应急决策方案。

遗传算法(GA)是模拟生物进化流程而开发的一种寻优算法。将遗传算法应用到供水工程渠道应急决策方案求解当中，其原理是通过遗传操作，不断淘汰“劣质”解，最后剩余最优解[15]。

(1)编码

对所要求解的目标模型的相关变量进行二进制编码。

(2)初始化种群

初始化种群，即列出所有满足目标模型的解。

(3)计算适用度值

以目标函数为基础，构建适应度函数，求解初始化种群的适用度值。适应度函数表达式如下：

(8)

式中，ψ(x)—适应度函数；g—一个比较大的非负数。

(4)遗传操作

遗传操作包括选择、交叉、变异3个步骤，通过这3个步骤选出最优个体，组成新的种群。选择、交叉、变异计算公式如下：

①选择：

(9)

②交叉：

(10)

③变异：

(11)

其中，

(12)

(13)

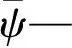
当经过遗传操作后，判断是否满足约束条件和最大迭代次数，若都满足，输出最优解，得出供水工程渠道应急决策方案[16]。

2 实际应用测试与分析

为测试基于遗传算法的长距离供水工程渠道应急决策方法的有效性，进行应用测试研究。

2.1 长距离供水工程渠道网络模型

以某研究区内的供水工程渠道为例，借助WaterGEMS建模软件建立网络模型，如图2所示。

在研究区内共有50条供水渠道，其中前15条渠道参数见表1。

2.2 遗传算法参数设置

利用遗传算法求解供水工程渠道应急决策方案时，所设置的初始化参数见表2。

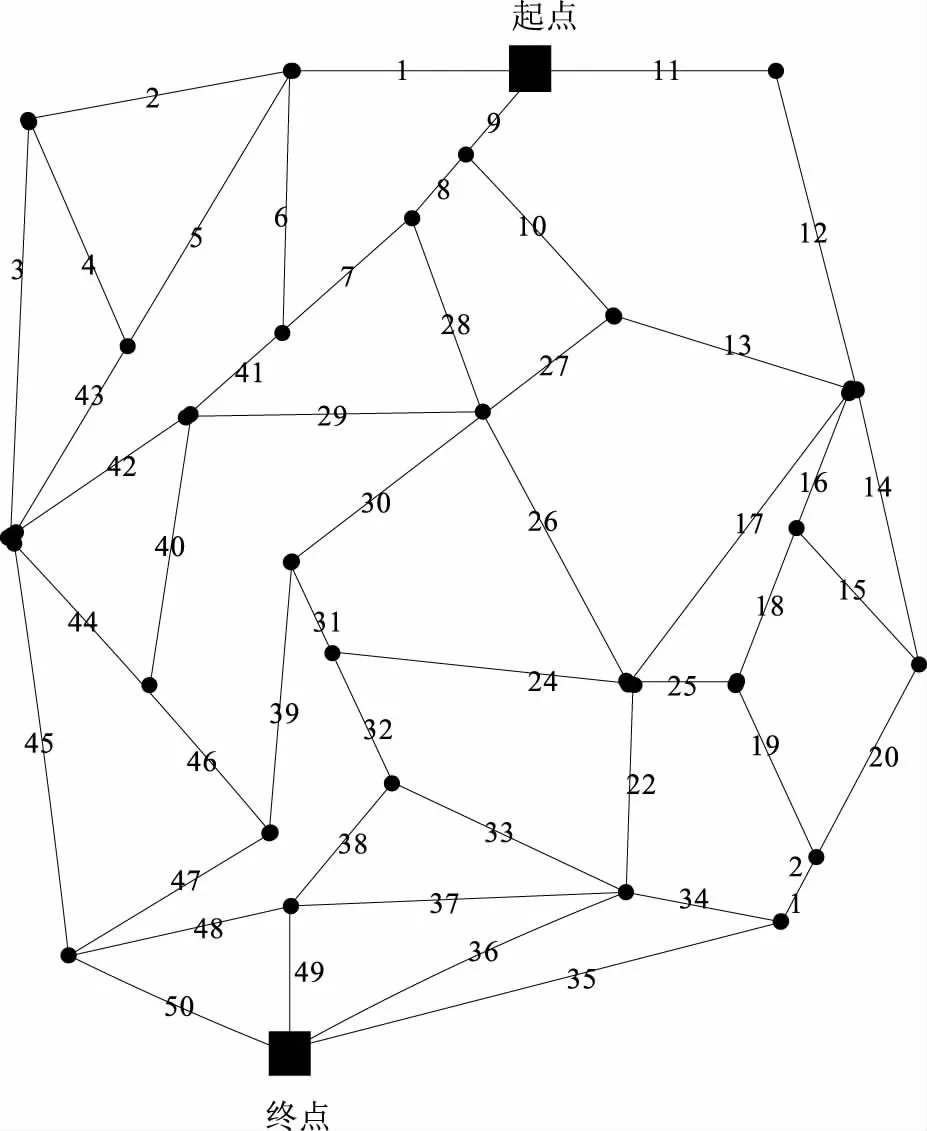
图2 长距离供水工程渠道网络模型

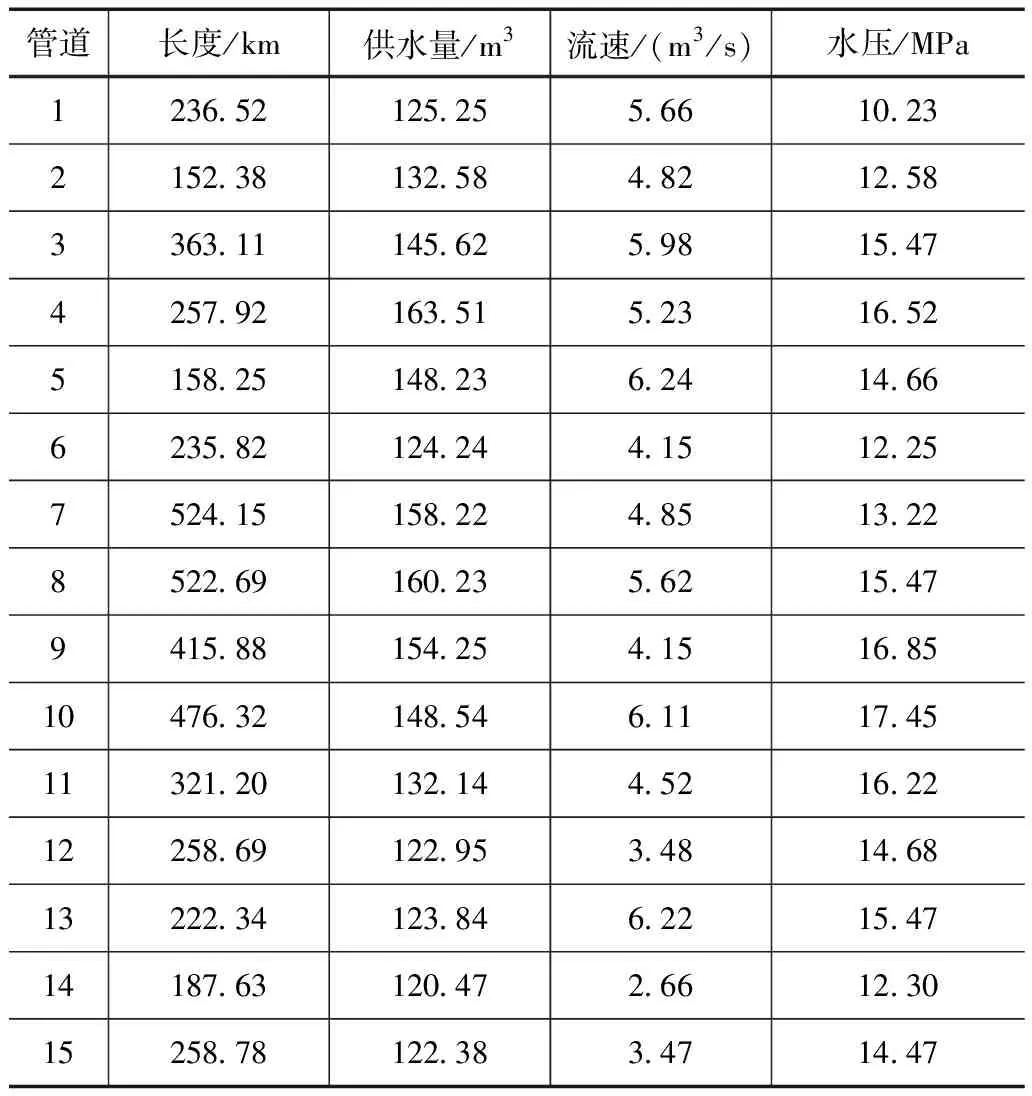
表1 长距离供水工程渠道参数(部分)

2.3 供水工程渠道应急决策方案

利用遗传算法求解供水工程渠道应急决策方案，求解结果如图3所示。

利用遗传算法求出3条渠道共同作用下，能满足目标模型，从而设计出供水工程渠道应急决策方案。

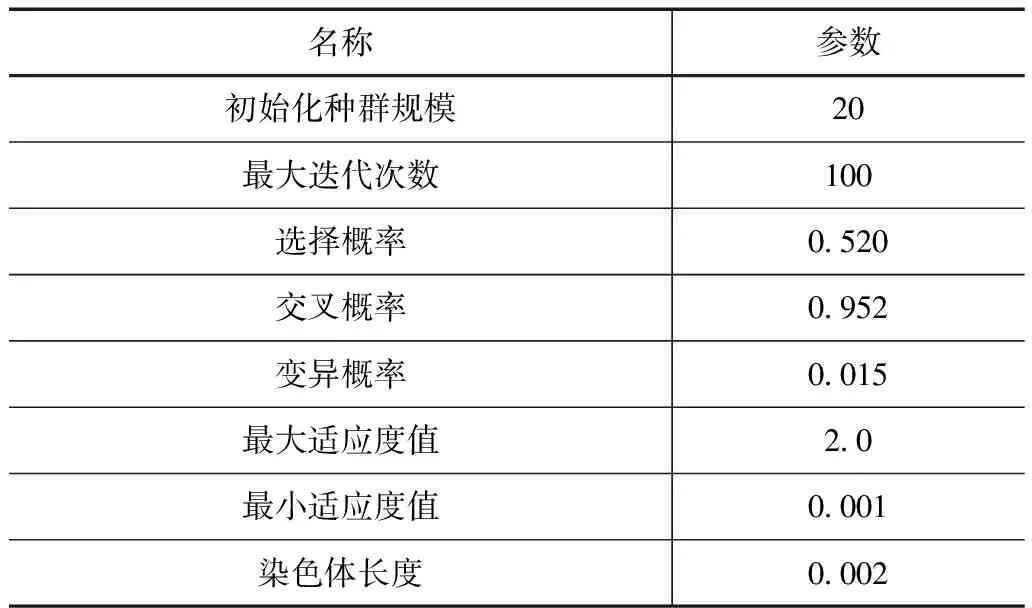
表2 遗传算法相关参数设置表

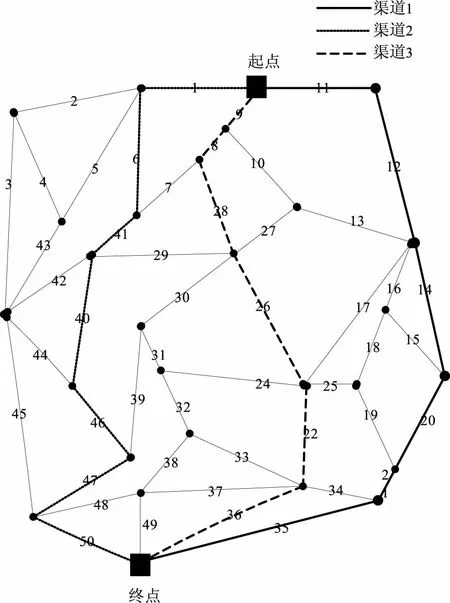
图3 供水工程渠道应急决策方案

2.4 方案合理性对比

为进一步测试所设计的供水工程渠道应急决策方案合理性，在同样条件下，利用基于NSGA- Ⅱ的方法、基于自适应多目标进化的方法进行求解，得出相应的应急决策方案，并以此作为对比项，最后统计不同应急决策方案运行后实际所需要的成本和供水量。结果如图4所示。

从图4中可以看出，与基于NSGA- Ⅱ的方法、基于自适应多目标进化的方法求得的应急决策方案相对比，本研究方法求得的应急决策方案运行所需要的成本更低且供水能力更强，说明本研究方法设计的应急决策方案更为合理。

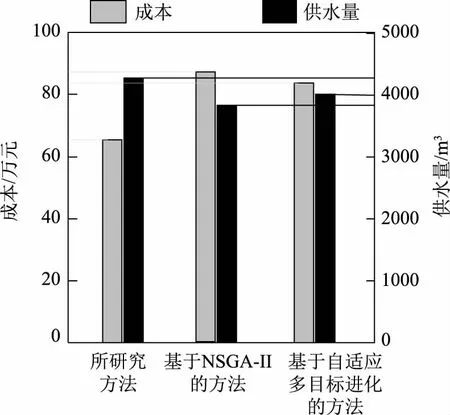
图4 不同应急决策方案运行所需要的成本和最大供水量

3 结语

受到地形、地势、气候、人口、经济等众多因素的影响，不同地区对水资源的需求量是不同的，这就造成有的地区水资源贫乏，无法满足人们生产、生活需求，因此需要进行水资源调配。供水工程是实现水资源调配的手段和途径。在面对紧急情况时，需要多条供水渠道一同运行，导致制定决策方案的难度上升。在此背景下，提出基于遗传算法的长距离供水工程渠道应急决策方法。在该研究中通过构建目标模型，并求解该模型，得出最优的决策方案。最后通过应用测试，证明了研究方法的有效性，同时证明了研究方法设计的决策方案更为合理，成本更低且供水能力更高。然而，本研究仍需要进一步研究，即所考虑的约束条件较少，导致求解较为困难，因此需要进行优化和改进。