基于深度学习的无人驾驶汽车车道跟随方法*

高扬 陈士伟 刘进渊 王书棋

（长安大学，西安 710054）

主题词：车道跟随 深度学习 注意力机制 循环神经网络 无人驾驶

1 前言

近年来，车道跟随作为无人驾驶领域的关键技术之一引起了广泛关注。在传统的连续帧车道跟随问题中广泛使用的是基于模型参数的方法，其中卡尔曼滤波是一种典型方法，例如Mammeri等人在跟踪车道线方面，使用了2个卡尔曼跟踪器来跟踪2个端点，但是单纯使用卡尔曼滤波器要求系统为线性且系统噪声需服从高斯分布，而在实际环境中，由于车辆振动，系统所处状态并不能满足这些条件。因此Kim 等人提出，车道跟随更适合用粒子滤波器而不是卡尔曼滤波器。然而粒子滤波器对参数空间中传播粒子的方差十分敏感，方差过大会使滤波效果变差，方差过小会造成搜索空间有限。于是，Heidi等人提出将粒子滤波器与卡尔曼滤波器结合为卡尔曼-粒子滤波器并在困难场景（乡村道路）下的车道跟随中取得了较为稳定的结果。

传统车道跟随方法在多变的道路场景中需要设计复杂的规则并进行繁琐的人工参数调整，不利于减轻人员负担，更不利于实现机器自我学习与自我控制。因此，近年来深度学习技术在车道跟随领域逐渐引起关注。Pomerleau 等人利用卷积神经网络实现了从驾驶图像到车辆转向盘转角的映射，在一定的野外条件下有效地实现了真实道路跟随；Muller 等人设计了6 层卷积神经网络，直接预测了车辆的转向盘转角来实现车道跟随；Bojarski 等人提出End-to-End 自动驾驶深度学习算法，并在仿真和真实驾驶场景中完成了测试；Yu 等人提出利用全卷积网络（Fully Convolutional Networks，FCN）进行更深层的语义分割，通过长短期记忆（Long Short-Term Memory，LSTM）网络直接对车辆转向盘转角和车速进行预测并取得了不错的效果。

就现有基于深度学习的车道跟随研究而言，车道跟随模型针对极端的困难驾驶场景（例如黑夜、阴影、无车道线等）的相关研究较少且准确性与稳定性较差，同时存在数据集制作成本高昂的问题。因此，本文结合一种多帧输入的车道线检测模型提出一种基于深度学习的无人驾驶汽车车道跟随模型。

2 基于深度学习的车道检测与跟随模型

2.1 时空信息与深层信息融合的车道线检测模型

本文基于U-Net结构提出一种基于时空信息与深层信息融合的车道线检测模型UNET_CLB（U-NET with Convolutional LSTM Block）。网络整体结构如图1所示，各部分作用为：编码器负责提取连续单目图像中的车道特征；卷积长短时记忆网络（CONVolutional Long Short-Term Memory，CONVLSTM）在经典LSTM 网络基础上用卷积操作代替矩阵乘法，通过LSTM网络保留时间信息，通过卷积操作保留空间信息，将编码器与解码器对应通道的多帧语义信息融合，获取更优的高级车道特征；解码器根据该特征恢复目标的语义信息。此外，编码器第4 层输出的一系列连续卷积块采用了密连卷积的思想，通过特征复用增强了网络的特征使用能力，以及通过不同层学习特征的并行映射增加了后续层的输入变化，即编码器第4层的输出经过密连卷积模块获取深层信息后输入CONVLSTM模块实现了深层信息的融合。整个网络模型的输入为车载单目相机采集的连续帧图像向量，输出为车道线语义分割预测图。

图1 车道线检测模型UNET_CLB

2.2 深度时间注意力的车道跟随模型

借鉴时空序列预测领域的经典模型PredRNN设计如图2 所示的时间注意力网络预测输入信息的相关性，并基于此建立基于深度时间注意力的车道跟随模型LSTM_DT（LSTM Network with Deterministic Time）。

图2 时间注意力网络结构

该模型包括输入层、中间处理模块以及输出层。

中间处理模块：

a.确定性注意力网络：使用LSTM 网络对先前的隐藏状态h进行更新并使用多层感知器对输入的维连续向量X进行加权。其中h∈R，基础的LSTM 单元可以总结为：

式中，i、f、o分别为输入门、遗忘门和输出门；c为当前时刻的细胞状态（Cell State）；[h;X]∈R为先前的隐藏状态（Hidden State）h和当前的输入X的堆叠；W,W,W,W∈R和b,b,b,b∈R分别为各门输入权重和每个分量的偏差，是网络需要学习的参数；()为Sigmoid激活函数；⊙为阿达马（Hadamard）乘积，即向量的元素相乘。

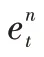
式中，v∈R、W∈R、P∈R为多层感知器需要学习的参数。

如图3所示，将连续时刻的车道线跟随数据以及车辆控制数据输入LSTM_DT 模型以预测时刻的车速与转向盘转角。网络整体结构由连续时刻的车道跟随数据、时间注意力网络、LSTM 单元，以及3 层全连接网络组成，其中每个LSTM 单元含50 个隐藏单元，全连接网络的第1 层和第2 层设为50 个神经元，最后一层设为2个神经元作为网络的输出向量y（时刻的车速和转向盘转角）。

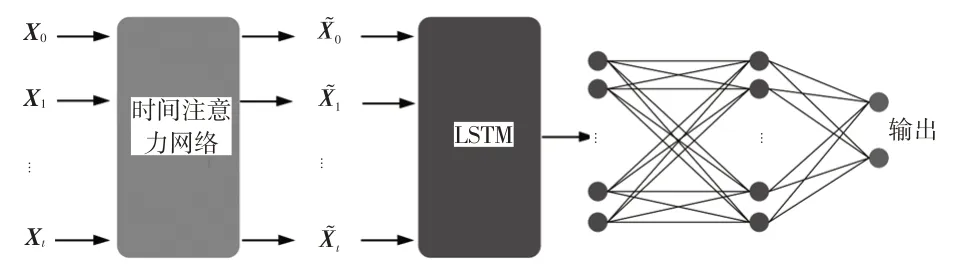
图3 车道跟随模型LSTM_DT

2.3 深度时空注意力的车道跟随模型

由于车道线跟随数据以及车辆控制数据经过时间注意力网络加权的车道向量输入LSTM 后，隐藏状态以及细胞状态会从时间空间映射到新的空间，为了保证新空间的历史信息的有效性，在LSTM_DT 基础上设计空间注意力网络为模型的隐藏状态增加权重，则优化后的LSTM_DTS（LSTM Network with Deterministic Time and Space）模型结构如图4所示。

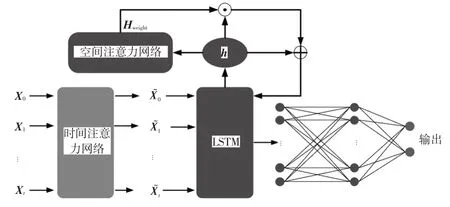
图4 车道跟随模型LSTM_DTS

如图4所示，输入的车道跟随数据经时间注意力网络加权输入LSTM单元，其隐藏状态通过SPACE_ATTNEN⁃TION层（空间注意力网络）加权以保证新空间的历史信息的有效性，用表示SPACE_ATTNENTION层，则加权后的LSTM单元可表示为：

3 自制车道跟随数据集的验证

为验证本文所提出模型的有效性，在自制车道跟随数据集上进行测试。针对单目相机采集的原始数据集经过初步的数据处理后，选择Labelme标注软件作为标记工具共制作60 000张车道数据集，涵盖黑夜、阴影、无车道线等困难驾驶场景，标注结果如图5所示。

图5 车道标记结果

如图5所示，为了评估UNET_CLB模型的车道线检测能力，本文对采集的图片进行了语义分割；为了便于获取车道线三次样条拟合参数以控制车道跟随行为，对图片进行了车道线实例分割。最后在车道线检测数据集的基础上建立车道跟随数据集（包含连续个时刻的两侧车道线跟随数据以及车辆控制数据），将(-1)时刻的车速和转向盘转角v、δ与时刻两侧车道跟随数据的三次样条参数值、、、、、、、作为车道跟随模型在时刻的输入数据；模型输出为时刻的车速和转向盘转角。

3.1 模型训练结果

车道跟随模型的输入为车道线三次样条参数与(-1)时刻的车速与转向盘转角，模型标签为时刻的车速与转向盘转角。模型训练时的时间步长设置为2；批量处理尺寸（Batch size）设置为64；训练时总的迭代次数（Epoch）设置为50；损失函数设置为均方误差（MSE）；优化器设置为自适应动量评估（Adam）；学习率设置为0.001。整个数据集按7∶1∶2 划分为训练集、验证集、测试集。本文模型的训练环境包含2台深度学习工作站，CPU为16核32线程的双路至强E5 2620，独立显卡分别为1 块GTX2080ti 和1 块GTX1080ti。深度学习环境配置为：CUDA 10.0、CUDNN 7.3.1、Pytorch 1.6.0、Python 3.7、OpenCV-Python 3.4以及其他相关依赖库。

如图6 为LSTM_DTS 模型在训练与验证中的误差变化曲线，可见模型训练误差在第3 次迭代时迅速下降，验证误差在第14 次迭代时基本不变，训练基本拟合，模型最终的训练误差、验证误差和测试误差分别为3.54%、1.75%、1.43%，可见模型在自制车道跟随数据集上的收敛速度较快，训练效果较好。如图7 所示为LSTM_DTS 模型在测试集上转向盘转角预测值与真实值结果（为了更好地衡量模型的预测效果，对原始数据和预测数据进行了归一化处理），由图7可知，模型对大部分数据都能较好地拟合。

图6 LSTM_DTS模型训练误差与验证误差曲线

图7 LSTM_DTS模型预测结果

3.2 模型对比测试

如图8 所示为本文所提出模型与经典时空预测模型PredRNN预测转向盘转角的结果对比曲线。可以看出，LSTM_DTS 模型预测结果变化较为平稳且更贴近真值，而PredRNN 模型在转角变化处产生剧烈波动。根据已有研究结果，前轮转角应满足约束：

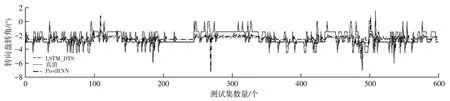
图8 转向盘转角对比曲线

式中，为稳定性因数；=9.8 m/s为重力加速度；为前轮最大转角；为模型车辆质心速度；为模型车辆的轴距。

可见，在较高车速下转向时采用PredRNN 模型预测结果会严重影响车辆的操纵稳定性，而采用本文所提出的LSTM_DTS 模型可以更好地克服转向盘转角的波动性从而具有更好的车辆操纵稳定性。

同样地，图9所示为本文所提出的模型与PredRNN模型在车速上的对比曲线。从图9 中可以看出，采用PredRNN 模型预测的车速变化剧烈，LSTM_DTS 模型预测的车速变化较为平稳且接近真实车速。而根据式（4），转角过大时，若超过对应转角下的极限车速会有发生侧滑的危险，可见LSTM_DTS模型不仅具有较高的准确率，并且可以很好地克服波动从而具有更好的车辆操纵稳定性。

图9 车速对比曲线

4 仿真验证

4.1 仿真环境下的验证

为进一步验证车道跟随模型在黑夜、阴影、无线等困难环境中能否满足车辆操纵稳定性，基于Webots 仿真软件搭建城市夜晚仿真模型。通过手动控制仿真车辆行驶，共采集6 000张黑夜环境车道图像制作车道线仿真数据集，同时记录对应时刻模型车的前轮转角与车速，并在其基础上制作车道跟随仿真数据集。利用车道线仿真数据集训练UNET_CLB模型，利用车道跟随数据集训练LSTM_DTS模型。

图10 给出了LSTM_DTS 的训练误差曲线，由图10可知，模型训练误差在第3 次迭代时迅速下降，验证误差在第8 次迭代时基本不变，模型训练基本拟合，模型最终的训练误差、验证误差和测试误差分别为3.65%、2.15%、2.27%，可见模型车道跟随仿真数据集上的收敛速度较快，训练效果较好。

图10 LSTM_DTS模型训练及验证误差曲线

如图11所示为采用本文模型进行整个仿真的算法框架：车道线检测类负责识别连续3 帧图像，并将最后一帧图像通过三次样条曲线拟合得到车道线参数；车道跟随类获取上一时刻的车道线参数，车速与前轮转角输出此时刻的车速和前轮转角；安全判定条件类判断车速与前轮转角是否符合极限关系，从而保证在满足安全条件的前提下控制仿真车辆行驶。

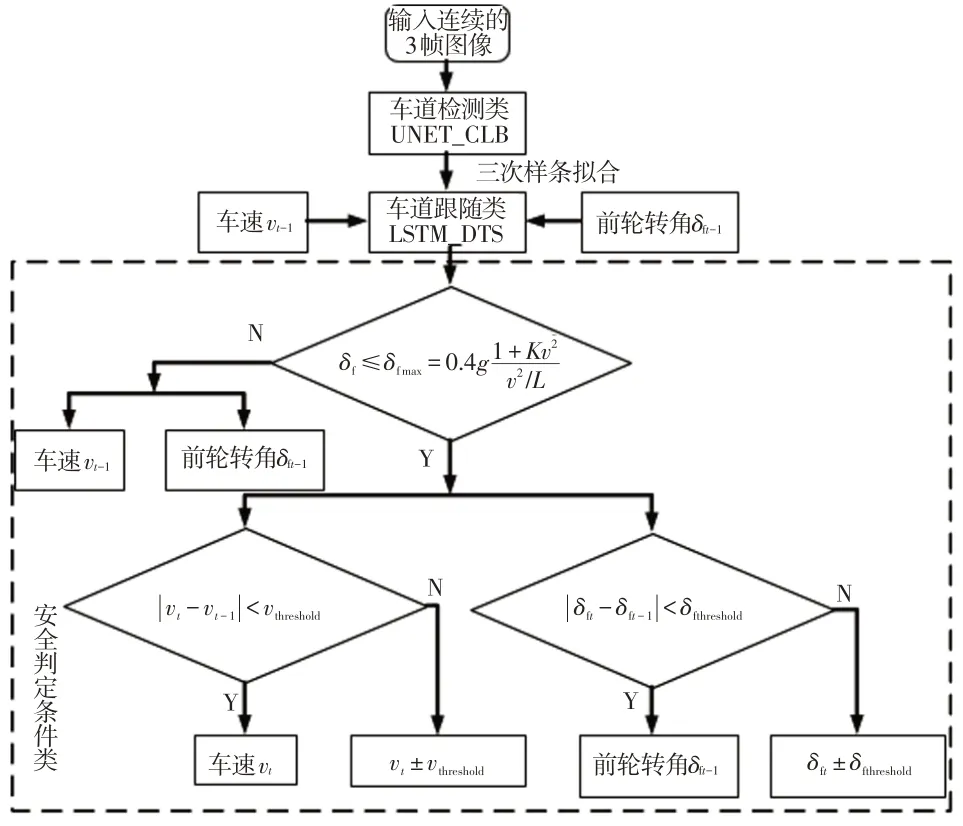
图11 仿真算法框架

基于常用的两轮车辆运动学模型，前轮驱动时，后轮转角恒为0，则车辆坐标系下的运动学模型为：

式中，为航向角；为质心侧偏角；、分别为模型车辆前轴轴距、后轴轴距。

PID 控制作为成熟的控制器被广泛应用在无人车轨迹跟踪领域，使用PID 控制作为对比方法检验LSTM_DTS 控制方法的有效性。将车道中间线的轨迹作为参考轨迹，利用无人车的横向跟踪误差e作为PID控制器的反馈，转向盘转角作为控制器的对象，其中横向跟踪误差e为前轴中心点(r,r)到最近路径点(p,p)的距离，具体如图12所示。

图12 横向跟踪误差示意

如图12，横向跟踪误差计算公式为：

式中，为前视距离，即后轴中心与当前最近路径点的距离；=-为前轴中心点(r,r)到最近路径点(p,p)间连线与垂直方向的夹角。

使用PID控制器输出转向盘转角为：

式中，e()为步对应的系统误差；k、k、k为控制器参数。

根据PID 控制器中比例控制（P）、积分控制（I）、微分控制（D）的控制特性，采用凑试法人工调节控制器对应的控制参数k、k、k使得横向误差达到较小值，同时对应观察仿真小车的运行轨迹与参考轨迹的对比来保证PID 控制器达到比较好的控制效果。PID 控制器的3 个参数通过凑试法确定，具体的取值为：k=1.0，k=0.001，k=20.0。

通过GPS记录仿真车辆的坐标（GPS无漂移），车辆在不同控制模型下的仿真路线与期望路线对比结果如图13所示。可见在黑夜环境中LSTM_DTS 控制下的车辆行驶路线基本符合期望轨迹，但在运行过程中出现一些困难点，导致车辆行驶路线发生波动。

图13 仿真结果对比

如图14所示为仿真车辆在困难点1、4、6（黑夜转弯处）UNET_CLB模型对车道线的识别结果。因为左车道线的像素点过少导致UNET_CLB 模型对左车道线拟合斜率出现偏差，从而影响LSTM_DTS 模型输出转角变小，但LSTM_DTS模型控制输出的结果较为平稳。

图14 UNET_CLB模型在黑夜转弯处的识别结果

如图15所示为仿真车辆在困难点2、3（阴影处），5、7（无车道线处）的识别结果。在阴影环境下UNET_CLB模型对车道线拟合效果良好，LSTM_DTS 模型在控制过程中由于即将进入转弯处，车速降低导致输出转角小幅波动但基本满足操纵稳定性要求；在无线环境下UNET_CLB模型受远端斑马线影响，导致车道拟合斜率偏差，LSTM_DTS模型在控制过程中输出转角小幅波动但基本跟随真实路线。

图15 UNET_CLB模型在阴影与无线处的识别结果

综上，在无车道线、阴影、黑夜等困难环境下LSTM_DTS模型输出控制转角虽然有较小的波动，但可以较好地控制仿真车辆安全行驶。与成熟的PID 控制器相比，本文所提出的控制方法有效避免了传统控制方法人工进行复杂的模型、规则、参数设计，并且只需提供足够的数据用于模型的训练即可达到与传统控制器相同的控制效果。

4.2 真实场景下的迁移学习验证

本节构建的仿真数据集与真实场景下的数据集具有相似性，因此选用迁移学习的方法对真实场景下构建的数据集进行训练与测试。UNET_CLB 模型在真实车道检测数据集的识别效果如图16所示。

图16 真实车道检测数据集识别效果

由图16 可知，UNET_CLB 模型在黑夜、阴影、无车道线环境中识别效果良好，并在存在车辙印、雨水等干扰条件下也具有较好的鲁棒性与较高准确率，为车道跟随模型LSTM_DTS 奠定了良好的跟随基础。如图17所示为LSTM_DTS 模型输出的预测值与真实值在转向盘转角上的对比曲线。从图17中可以看出，LSTM_DTS模型与真实数据差值基本在0附近波动，具有较好的平顺性，在真实转角剧烈变化处，模型预测值偏小，因此本模型可以更好地克服波动使得车辆保持良好的车辆操纵稳定性。

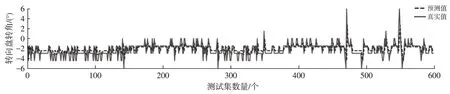
图17 迁移学习下的转向盘转角对比曲线

同样地，如图18 所示为LSTM_DTS 模型输出的预测值与真实值在车速上的对比曲线。在车速剧烈变化时，LSTM_DTS 模型输出的车速预测值相对较小，有助于保证车辆的驾驶安全性；在车辆直线高速行驶时，LSTM_DTS 模型的预测值与真实值比较接近而且变化平稳，保证了驾驶员的操纵稳定性。

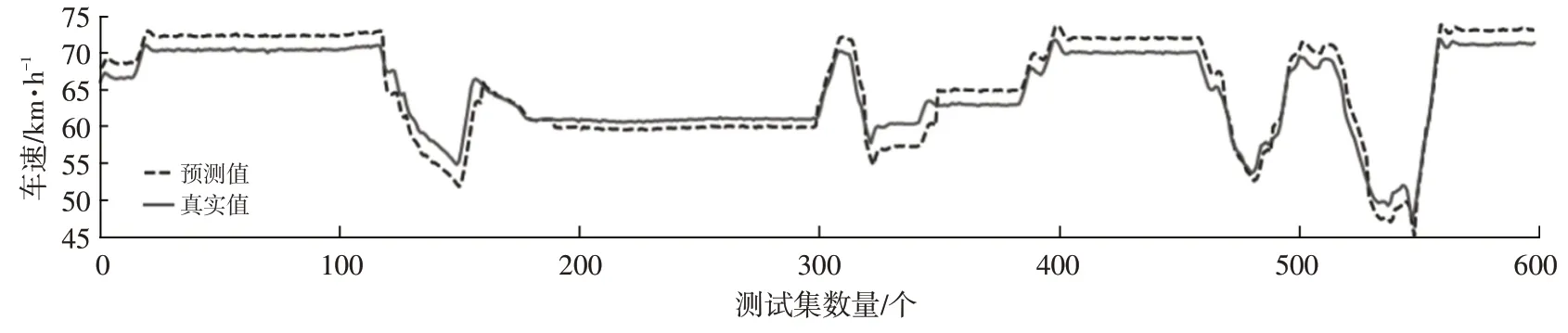
图18 迁移学习下的车速对比曲线

5 结束语

本文提出了一种深度时空注意力网络与循环神经网络相结合的车道跟随模型LSTM_DTS，并在自制的实际车道跟随数据集上训练取得了1.43%的测试误差。最后结合一种多帧输入的车道线检测模型UNET_CLB在搭建的仿真困难驾驶场景（包含黑夜、阴影、无车道线等）下对本文所提出的模型进行训练以及测试验证，获得了2.27%的测试误差，并通过迁移学习方法进行验证，结果表明，本文模型不仅具有良好的鲁棒性与准确性，并能够在困难场景下有效地实现无人驾驶车辆车道跟随，可以更好地辅助无人驾驶并能应用于车道偏离预警、自动泊车等无人驾驶技术。