长径比对弹体斜侵彻多层混凝土靶姿态影响研究

张 博，张丁山，吕永柱，赵永刚，全嘉林

(西安近代化学研究所，西安 710065)

1 引言

地面建筑物目标是钻地弹的重点打击对象，一般为多层钢筋混凝土结构。李江涛等研究了不同着角和速度对弹丸侵彻多层钢混靶的弹道特性；吴普磊等研究了攻角对弹体斜侵彻多层混凝土靶的弹道偏转影响；李鹏飞等研究了2种不同头部结构弹体斜侵彻多层混凝土靶的偏转规律；刘宗伟等建立了弹丸斜侵彻多层混凝土靶的弹道姿态计算模型；朱战飞等研究了钢混靶间距及层数对弹体斜侵彻弹道性能的影响；其他许多学者对弹体斜侵彻混凝土的机理及模型进行了深入研究，但是由于力学模型的缺乏，关于弹体参数对斜侵彻多层混凝土靶的姿态偏转影响研究相关文献较少。

为此，本文针对长径比对弹体斜侵彻多层混凝土靶姿态偏转影响的问题，采用数值仿真及次口径侵彻试验研究了不同长径比弹体在710 m/s初速、10°着角情况下侵彻5层混凝土靶的姿态偏转规律；结合弹体受力情况，从理论上定性分析了长径比对弹体姿态的影响规律，为钻地弹的结构设计提供参考。

2 试验研究

2.1 试验弹体结构参数

弹体由壳体、装药及后盖组成,如图1所示。壳体及后盖材料为G50钢，内部装药为HMX炸药，各材料主要性能参数列于表1中。3种弹体方案参数列于表2中，为弹体长度，为弹体质心到弹体前端面长度，为弹体外径，为弹体头部弧段半径，为弹体质心比，为弹体曲径比；在方案设计中通过调整内部结构保证3种弹体结构质心比相同。

图1 弹体结构示意图Fig.1 Schematic diagram of projectile structure

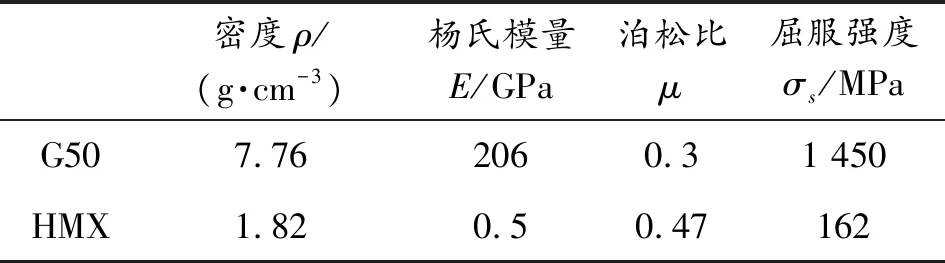
表1 弹体材料主要性能参数Table1 The mechanical parameters of projectile

表2 3种方案弹体结构参数Table 2 The structural parameters of three projectiles

2.2 试验过程

根据表2参数加工试验弹体，如图2所示。弹体采用320 mm平衡炮次口径发射，利用高速摄影对弹体侵彻混凝土靶全过程进行追踪记录，试验后分析弹体的速度及偏转情况。5层混凝土靶如图3所示，试验前实测混凝土靶抗压强度为41.3 MPa；第1层厚度300 mm，后4层厚度为180 mm，靶面垂直间距2 mm，靶面与水平夹角80°；第1～3层靶迎弹面尺寸为1.5 m×1.5 m，第4～5层靶迎弹面尺寸为2 m×2 m；试验现场布局如图4所示。

图2 弹体实物图Fig.2 Experimental projectile

图3 5层混凝土靶实物图Fig.3 Experimental concrete targets

图4 试验现场布局示意图Fig.4 Layout of the experiment

2.3 试验结果及分析

弹体侵彻5层混凝土靶后完整回收，弹体未出现弯折或断裂，如图5所示。3种长径比弹体侵彻过程如图6～图8所示，弹体偏转角度为弹体轴线与水平方向夹角，试验结果列于表3。

图5 回收弹体状态图Fig.5 Projectile after the test

图6 长径比4.01弹体侵彻过程示意图Fig.6 Penetration process of the projectile with length-diameter ratio 4.01

图7 长径比4.46弹体侵彻过程示意图Fig.7 Penetration process of the projectile with length-diameter ratio 4.46

图8 长径比4.92弹体侵彻过程示意图Fig.8 Penetration process of the projectile with length-diameter ratio 4.92

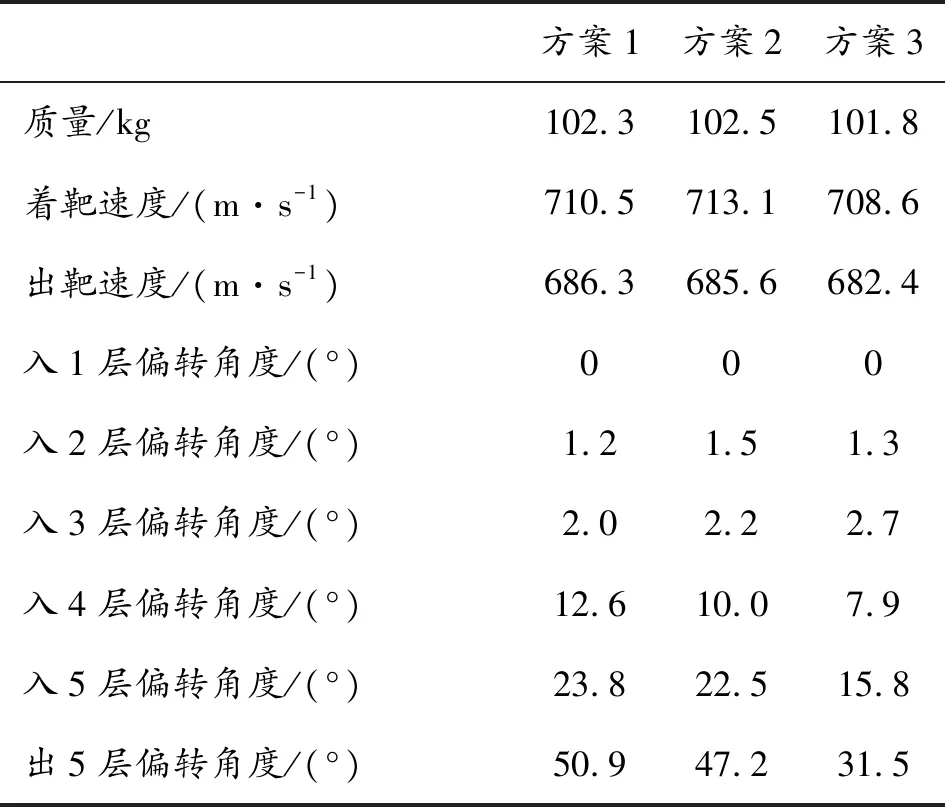
表3 试验结果Table 3 The experimental results

如图9所示，随着长径比增大，弹体偏转角度逐渐减小；长径比从4.01增加至4.92时，偏转角度从50.9°减小至31.5°，减小38.11%。

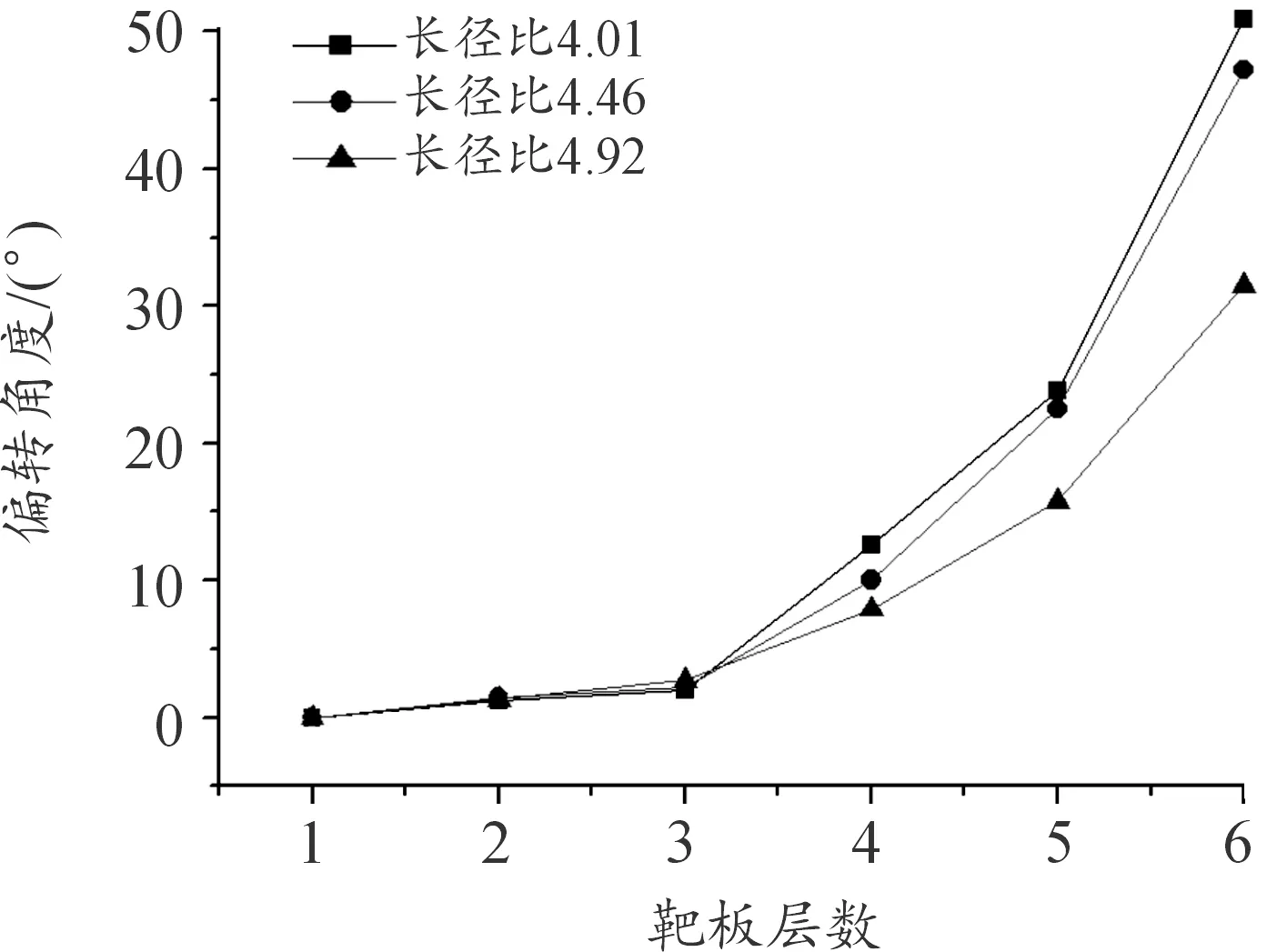
图9 3种长径比弹体试验偏转角度曲线Fig.9 Comparison of experimental trajectory deflection angle of three length-diameter ratio projectiles

3 数值仿真计算研究

3.1 数值仿真模型

利用ANSYS/LS-DYNA 软件，依据表2弹体参数及试验中靶板尺寸建立数值仿真模型，如图10所示。壳体及后盖G50材料选用带应变率效应的Johnson-Cook材料模型；内部装药材料选择Plastic-Kinematic模型；混凝土靶采用HJC强度模型，密度为2 440 kg/m，抗压强度为41.3 MPa；HJC模型的主要性能参数见表4。

图10 数值仿真模型示意图Fig.10 Schematic diagram of projectile and target

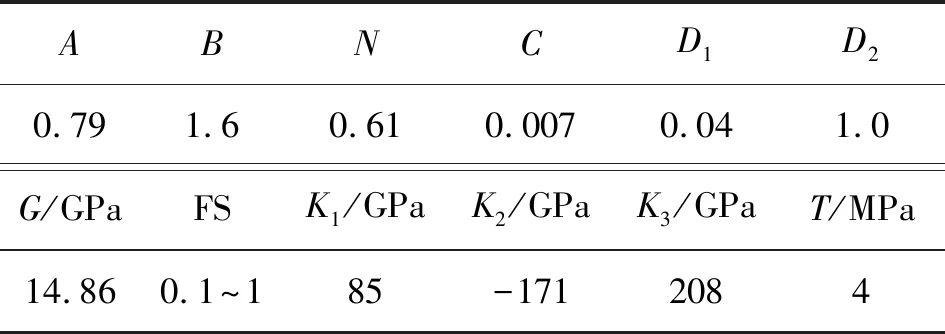
表4 混凝土HJC模型主要参数Table 4 Parameters of HJC model for concrete

3.2 计算结果

对3种长径比弹体方案进行数值仿真计算，初速为710 m/s，着角10。计算完成后读取撞靶时刻弹体姿态偏转角度，列于表5中。弹体偏转角度随靶板层数增加变化情况如图11～图13所示。

图11 长径比4.01弹体数值仿真结果云图Fig.11 Simulation results of the projectile with length-diameter ratio 4.01

图12 长径比4.46弹体数值仿真结果云图Fig.12 Simulation results of the projectile with length-diameter ratio 4.46

图13 长径比4.92弹体数值仿真结果云图Fig.13 Simulation results of the projectile with length-diameter ratio 4.92

表5 数值仿真结果Table 5 Simulation results

图14为3种长径比弹体数值仿真偏转角度曲线。

图14 3种长径比弹体数值仿真偏转角度曲线Fig.14 Comparison of numerical simulation trajectory deflection angle of three length-width ration projectiles

3.3 试验结果与仿真结果对比

图15～图17为3种长径比弹体偏转角度试验结果与仿真结果曲线，试验测得出靶速度与数值计算最大偏差为 8.25%，弹体出靶偏转角度与数值计算最大偏差为8.06%，数值仿真计算结果与试验结果符合较好。

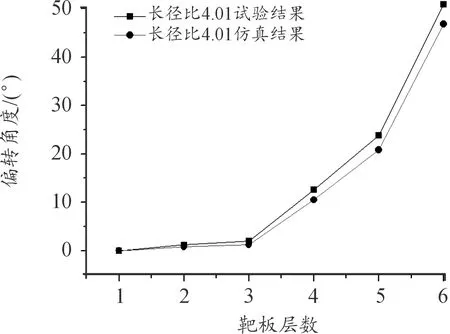
图15 长径比4.01弹体试验与仿真结果曲线Fig.15 Comparison of experimental and numerical simulation of the projectile with length-diameter ratio 4.01

图16 长径比4.46弹体试验与仿真结果曲线Fig.16 Comparison of experimental and numerical simulation of the projectile with length-diameter ratio 4.46

图17 长径比4.92弹体试验与仿真结果曲线Fig.17 Comparison of experimental and numerical simulation of the projectile with length-diameter ratio 4.92

4 数值仿真及试验结果分析

结合试验及数值仿真结果，将弹体侵彻单层混凝土靶过程分为3个阶段，如图18所示。图中为战斗部质心，为等效阻力中心，为战斗部速度，为靶对战斗部的等效作用力。第一阶段弹体头部侵入靶板，如图18(a)所示，弹体头部受到靶板的反作用力，此时由于着角的存在，作用在弹体头部的等效作用力为不对称力，且等效阻力中心距离质心远，对弹体产生较大的偏转力矩，导致弹体发生偏转；第二阶段随着弹体向前运动，弹体中部进入靶板，如图18(b)所示，此时等效阻力中心逐渐靠近质心，作用力对弹体产生的偏转力矩减小；第三阶段是弹体尾部出靶板的过程，如图18(c)所示，由于第一阶段偏转力矩的作用，弹体产生偏转角速度，在尾部出靶时靶板对弹体的等效作用力产生的偏转力矩将与第一阶段的偏转力矩方向相反，且随着等效阻力中心逐渐远离质心，弹体所承受的偏转力矩随之增大，使弹体向着与第一阶段相反的方向偏转。

图18 弹体侵彻混凝土靶受力过程示意图Fig.18 Schematic diagram of projectile penetrate the concrete target

弹体在侵彻后续混凝土靶时受力状态与首层类似，主要区别为3个阶段偏转力矩方向的不同，可归结为第一阶段弹体偏转，第二阶段随进，第三阶段修正(反向力矩)。

弹体初始动能一定时，随着长径比增大，弹体在穿靶过程中所承受的偏转力矩及修正力矩均增大。结合试验及仿真结果得出，所设计的3种长径比弹体方案在侵彻5层混凝土靶过程中偏转力矩对弹体的作用大于修正力矩；随着长径比的增大，修正力矩的作用增加幅度大于偏转力矩，因此弹体偏转角度降低。弹体偏转角度随长径比的增加近似为指数性降低，如图19所示。

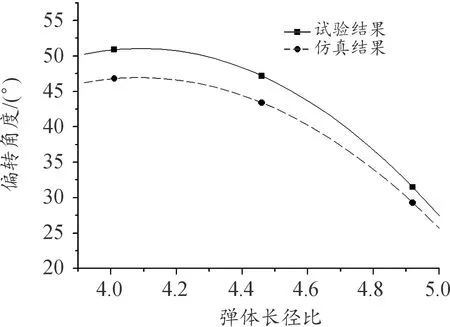
图19 弹体偏转角度随长径比变化曲线Fig.19 The curve between trajectory deflection angle and length-diameter ratio of projectile

5 结论

1)在初始动能相同条件下，弹体偏转角度随长径比增大而减小；

2)弹体长径比从4.01增加至4.92时，偏转角度从50.9°减小至31.5°，减小38.11%；

3)试验中出靶弹体偏转角度与数值仿真结果最大偏差为8.06%，数值仿真模型计算精度较高。