阶梯式双层EFP成型及侵彻性能数值模拟
杨朝霞,陈智刚,杨宝良,程 瑶,张晓东,赵太勇,王维占
(1.中北大学 机电工程学院,太原 030051;2.中北大学 地下目标毁伤技术国防重点学科实验室,太原 030051;3.西安现代控制技术研究所,西安 710065;4.西北机电工程研究所,陕西 咸阳 712099)
1 引言
近几年,由于爆炸反应装甲、复合装甲技术不断创新,传统破甲战斗部面临着艰难的考验。多层药型罩串联EFP具备更加严谨的能量转化与吸收机理,化学能利用率也极高并且可以增加弹丸的毁伤效应,因而引起广大学者研究。
国外和国内先后都对多层EFP的成型模型、成型机理进行了仿真研究及试验分析。但研究都是针对传统的双层EFP,其成型及侵彻效能仍具不足。王维占等对包覆式双层EFP成型进行了数值模拟研究,杨帅建立了前后级爆炸成型弹丸飞行速度的理论计算模型,分别得出实现双层EFP的包覆或分离的结构参数取值范围,为本文数值模拟研究提供一定参考。
Liu等发现尾翼结构对EFP气动特性有很大提高;张孝中等通过有限元模拟在药型罩外表面刻制矩形凹槽,得到了成型较好的尾翼EFP;杨宝良等分析了阶梯式药型罩阶梯旋角等参数与EFP尾翼偏斜角等的关系,为EFP气动特性的优劣评估提供参考依据。由此可见,阶梯结构及尾翼结构对EFP综合性能的提高大有裨益。
故本文提出了一种阶梯式双层EFP结构,利用数值模拟的方法复现了双层阶梯型EFP的成型过程,主要研究了装药长径比、药型罩壁厚、曲率半径对双层串联阶梯型EFP的成型特性的影响规律,并探究了阶梯式双层EFP对移动目标的侵彻效能。研究结论对爆炸成型弹丸战斗部结构设计具有一定的指导意义。
2 装药结构方案与计算模型
本文设计外罩内表面为阶梯型,内罩外表面为阶梯型来进行仿真计算,如图1所示。图2中左图为战斗部结构示意图,、分别为装药高度与直径,、、分别为外球、中球、内球的半径。如图2中右侧图所示,仿真模型中罩底内口径为80 mm,装药直径为80 mm。

图1 双层罩有限元模型示意图Fig.1 Finite element model of double-layer liner

图2 实体模型与计算模型示意图Fig.2 Solid model and simulation model
通过TRUEGRID建模软件构建仿真模型,由于药型罩为阶梯型,建立整体结构的三维模型。计算网格是Solid164八节点六面体单元,装药结构各部分均使用拉格朗日算法,炸药与药型罩之间采用侵蚀接触,其余为自动面-面接触算法。本文数值模拟中,战斗部装药为8701炸药,材料模型为HIGH_EXPLOSIVE_BURN,状态方程为JWL,主要参数见表1。内外层药型罩都选取紫铜这一材料,战斗部壳体材料为45钢,全部金属采用JOHNSON-COOK材料模型,状态方程为GRUNEISEN,主要参数见表2。

表1 8701 炸药参数Table 1 Parameters of 8701 explosive

表2 金属材料参数Table 2 Parameters of metal material
其中:为屈服应力;为应变硬化系数;为应变硬化指数;为应变率相关系数;为温度相关系数。
3 阶梯式双层EFP成型过程分析
阶梯药型罩是在药型罩外端面或者内端面相对于半径法线的镶块错位。在阶梯药型罩压垮过程中,产生角动量传递给药型罩而且得以保持,使弹丸在空中飞行时通过旋转来保证气动力稳定性。
双层阶梯型聚能装药结构由壳体、炸药和内外层药型罩组成。其中,靠近炸药的为外罩;远离炸药的为内罩。双层EFP的成型过程如图3所示。

图3 双层EFP的成型过程Fig.3 Forming process of double-layer EFP
内外层药型罩最先垮成饼状(24 μs),无明显的非对称性。随着药型罩顶部和轴向边缘的速度梯度的增加,EFP逐渐被拉长,雏形尾翼逐渐形成(92~164 μs)。不论阶梯结构位于药型罩内表面还是外表面,药型罩的阶梯结构在EFP成型过程中,成为凹陷导槽与凸出尾翼翼片的分界位置。其中,药型罩阶梯外侧位置药型罩壁厚较薄,该处药型罩质量微元在成型过程中发生径向收缩,形成凹陷结构的尾翼导槽。而药型罩阶梯内侧位置药型罩壁厚相对较厚,在EFP成型过程中此处质量微元发生径向折叠扩张行为,形成凸出结构的尾翼翼片。因为药型罩自身材质的抗力特性,径向凹陷收缩与凸出折叠扩张的质量微元运动一定位移后停止运动,此时药型罩形成带有褶皱状且周向均匀分布的尾翼式EFP,整个EFP成型过程结束(=276 μs)。内外罩成型稳定后,由于存在一定速度差,飞行一段时间后逐渐分离(276~396 μs)。
双层罩毁伤元形成机理与其形状密切相关。小锥角药型罩通过压垮形成毁伤元,内外罩间的摩擦阻力非常小,两罩难以分开。球缺罩通过翻转形成毁伤元。阶梯式球缺罩有益于产生形状更好、长径比更大的EFP,而且成型弹丸产生了旋转,在空中能够稳定飞行前进。在忽略其他条件下,阶梯式球缺罩性能更加优良,因而能以球缺罩为基础来不断发展完善阶梯式旋转EFP技术。
4 成型及侵彻效能因素分析
4.1 阶梯结构影响
当内外层药型罩壁厚均为5.5 mm,装药长径比为1.4时,分别对传统式双层药型罩结构和阶梯式双层药型罩结构进行数值模拟,对比分析2种结构下双层EFP的速度、长径比以及转速。
由表3可知,阶梯式双层药型罩结构的内外层EFP速度均大于传统式;阶梯结构的内外层EFP长径比相差较小,而传统结构内外层EFP长径比相差较大,且外层EFP长径比偏大,容易产生拉伸断裂;阶梯结构的双层EFP具有一定转速,而传统结构的双层EFP几乎没有转速。综合分析可知,相比于传统式双层药型罩结构,阶梯式双层药型罩结构所形成的双层EFP既可以在空中高速稳定飞行,又不易产生断裂且侵彻威力足够。

表3 2种结构下的双层EFPTable 3 Double-layer EFP comparison of two structures
4.2 装药长径比影响
从双层EFP速度、长径比、转速角度研究,内外层药型罩壁厚均取5.5 mm,依次改变装药长径比,进行数值模拟。
由表4发现,药型罩形成带有褶皱状且周向均匀分布的尾翼式EFP。当药型罩壁厚一定时,装药长径比越大,外罩EFP尾部越收拢。根据图4不难看出:装药长径比越大,内外罩EFP速度越高,内罩EFP速度始终大于外罩EFP。内外罩EFP长径比与装药长径比呈正相关;装药长径比大于1.3时,内外罩EFP长径比相差较小。装药长径比小于1时,内外罩EFP转速随着装药长径比的增加而逐渐增加;大于1时,内外罩EFP转速先减小后增加再减小。当装药长径比为1.6时,内罩EFP负向转速最大且外罩EFP正向转速最大。通过上述分析得出装药长径比取值在1.5~1.6较好。
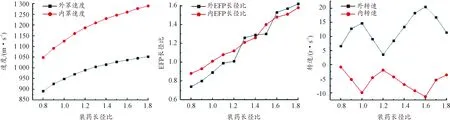
图4 装药长径比-EFP成型特性曲线Fig.4 The forming characteristics of EFP vs.the ratio of length to diameter of charge

表4 不同长径比条件下的双层EFP对比Table 4 Comparison of double-layer EFP under different ratios of length to diameter
4.3 药型罩壁厚影响
从双层EFP速度、长径比、转速角度研究,在装药长径比为1.5时,依次改变药型罩壁厚,进行数值模拟。
由表5和图5发现,随着药型罩壁厚的增加,内外罩EFP的速度都呈逐渐减小的趋势,内罩EFP速度始终大于外罩EFP。内外罩EFP的长径比随药型罩壁厚的增加逐渐减小,药型罩壁厚小于5.5 mm时,外EFP长径比与内EFP长径比相差不大;药型罩壁厚大于5.5 mm时,外EFP长径比小于内EFP长径比,两者差值逐渐增大。当EFP长径比过大时,容易产生拉伸断裂;EFP长径比过小时,会造成EFP空腔,影响破甲能力,因而双层EFP的长径比都要保持在一定合理范围内。随着药型罩壁厚的增加,内外罩EFP转速均逐渐减小直至为0。综合分析可知内外罩药型罩壁厚取值在 5~5.5 mm较好,既可以保证双层EFP在空中高速稳定飞行,又可以使得双层EFP不容易断裂且有足够的侵彻威力(表5)。

图5 药型罩壁厚-EFP成型特性曲线Fig.5 The forming characteristics of EFP vs.the thickness of liner

表5 不同药型罩壁厚条件下的双层EFP对比Table 5 Comparison of double-layer EFP under different thicknesses of liner
4.4 曲率半径影响
依次改变内外罩曲率半径比(与装药直径之比),进行数值模拟,表6为曲径比与双层EFP速度、长径比、转速之间的关系。
由表6和图6可知:随着曲径比的增大,外罩EFP速度逐渐增大,内罩EFP速度逐渐减小。内外罩EFP的长径比随曲径比的增大都逐渐减小,但EFP长径比过小时,破甲能力有所下降。随着曲径比的增加,内外罩EFP的转速均逐渐减小,直至为0。综合分析,当内外罩曲径比在0.96~1.38时,弹丸既可以保证较高的飞行稳定性,又具备足够的侵彻威力。
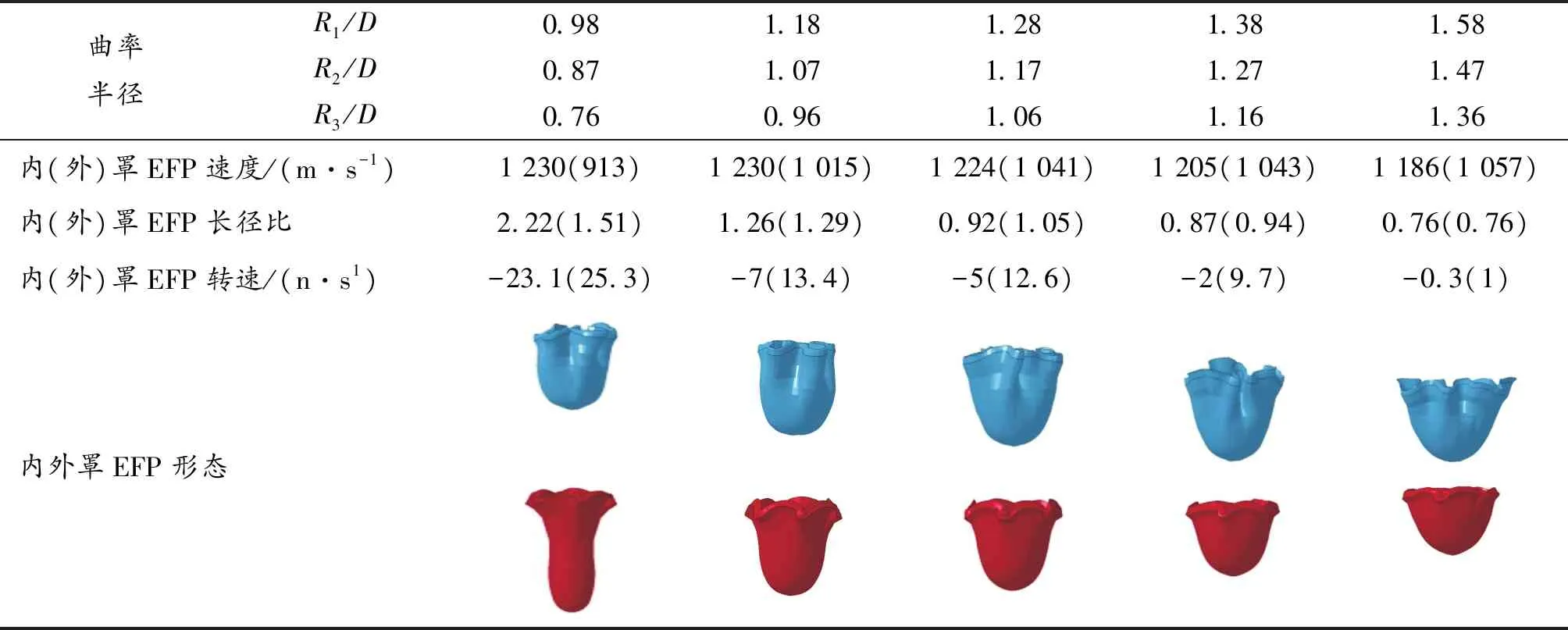
表6 不同曲径比条件下的双层EFP对比Table 6 Comparison of double-layer EFP under different ratios of curved diameter

图6 中曲径比-EFP成型特性曲线Fig.6 The forming characteristics of EFP vs.the ratio of curved diameter
4.5 侵彻效能
经上述分析可知,研究设计的双层阶梯旋转EFP可在不同结构参数下成型形态和前后EFP分离距离不同,这将导致EFP的终点弹道对装甲目标的毁伤效能具有显著影响。研究选定美国LAV-25轮式步兵战车为研究对象,选取其易损件(正面首上装甲)等效靶为12 mm RHA钢靶,作为双层阶梯EFP的侵彻目标,炸高分别为1 m、10m、30 m、60 m、100 m,靶板等效为长100 cm、宽30 cm、厚度10 mm的移动装甲钢,速度为24 m/s(车辆移动的时速)。
双层EFP侵彻移动靶时,由于内外罩EFP速度大小有所差异,内罩EFP首先接触到靶板并将其穿透,此时外罩EFP距离靶板存在一定距离;当外罩EFP接触到靶板时,靶板已经移动一段距离,因此2个EFP所造成的穿孔具有一定距离。由图7可知,炸高小于10 m时,双层EFP侵彻移动靶形成2个相连孔;炸高大于10 m时,双层EFP侵彻移动靶形成2个具有一定距离的孔;炸高越大,2个孔的间距就越大。

图7 长径比为1.1时,不同炸高下双层EFP对移动靶的侵彻示意图Fig.7 Penetration results of double-layer EFP to moving target under different standoff distances when the ratio of length to diameter is 1.1
由图8~图10可知,本文所设计的双层阶梯型聚能装药结构可实现对移动靶的多孔毁伤效应。结合3.2~3.4节可知,移动靶板的穿孔间距主要与前后级EFP的成型速度具有相关性,而前后级成型EFP速度与装药结构参数密不可分。根据图11可以发现,炸高大于10 m时,炸高越大,双层EFP侵彻移动靶所形成的两孔的间距越大。炸高为100 m时,随着长径比的增大,双层EFP侵彻移动靶所形成的2个孔的间距基本一致;随着药型罩壁厚的增加,靶板上的2个孔的间距越来越大;随着曲径比的增大,靶板上的2个孔的间距越来越小。

图8 炸高100 m时不同长径比条件下双层EFP侵彻移动靶形成的双孔图Fig.8 Double punching figures of double-layer EFP to moving target under different ratios of length to diameter when the standoff distance is 100 m

图9 炸高100 m时不同药型罩壁厚条件下双层EFP侵彻移动靶形成的双孔图Fig.9 Double punching figures of double-layer EFP to moving target under different thicknesses of liner when the standoff distance is 100 m

图10 炸高100 m时不同曲径比条件下双层EFP侵彻移动靶形成的双孔图Fig.10 Double punching figures of double-layer EFP to moving target under different ratios of curved diameter when the standoff distance is 100 m

图11 两孔间距随炸高、装药长径比及药型罩参数变化曲线Fig.11 The distance double punching vs.standoff distance、ratio of length to diameter of charge and structural parameters of liner
5 结论
1)双层阶梯型聚能装药战斗部可形成分离式双层旋转EFP。药型罩结构参数对EFP成型特性的影响非常关键,装药长径比在1.5~1.6,内外罩壁厚在5~5.5 mm,曲径比在0.96~1.38时,双层EFP能够在空中高速稳定飞行且成型较好,既不容易拉伸断裂,又有足够的侵彻威力。
2)双层阶梯型聚能装药战斗部可实现对装甲目标的双开孔效应。炸高越大,双层EFP侵彻移动靶所形成的两孔的间距越大;装药长径比增大,两孔间距基本不变;两孔间距与药型罩壁厚呈正相关,与曲径比呈负相关。
研究结论可为战斗部结构发展提供参考。

