坡度影响下的砒砂岩区裸露坡面水分入渗特征及模拟
吴佩瑶,秦富仓,2,董晓宇,李 艳,孙 成
(1.内蒙古农业大学沙漠治理学院,呼和浩特 010018;2.内蒙古农业大学林学院,呼和浩特 010019)
砒砂岩是指集中分布于黄土高原北部晋陕蒙接壤地区的一种松散岩层,交错层理发育且颜色混杂,通常以粉红色、紫色、灰白色互层相间而存在。成岩程度低、颗粒间胶结性差和岩层结构松散的特点导致其抗蚀能力差,加之在重力、风力和雨水等外部因素的复合侵蚀下,其分布区内水土流失严重,生态环境恶劣。根据地表覆盖区情况,通常将砒砂岩区分为附土砒砂岩区、覆沙砒砂岩区和裸露砒砂岩区。其中裸露砒砂岩区植被稀少、覆盖度极低,基岩大面积裸露,以水蚀为主、复合侵蚀严重,且面积超过砒砂岩区总面积的70%。而裸露砒砂岩区的坡面是土壤侵蚀作用的基本单元,作为地形因子之一的坡度与坡面侵蚀密切相关。因此本研究对象对于砒砂岩区的土壤侵蚀治理具有一定的广泛性和代表性。内蒙古砒砂岩区是黄土高原水土流失最严重的区域之一,对该区土壤水分运移过程的了解和掌握一直是亟待解决的难题。其中土壤水分入渗作为“四水”转化的中心环节,涉及到土壤水分再分布、地表径流和降雨补给等诸多方面。因此,研究砒砂岩区不同坡度条件下裸露坡面的土壤水分入渗过程及规律,对认识降雨入渗对砒砂岩区的侵蚀机理、制定水土保持方案具有一定意义。
目前关于土壤水分入渗规律的研究成果十分丰富,诸如基于物理意义、半经验模型和经验模型的众多经典理论,且对于特定约束条件下的入渗规律探究依旧是当下的研究热点。相关研究表明,土壤的入渗过程受到多种因素的综合影响。吴军虎等通过不同有机质含量的土壤入渗试验,得到容重对质地相同而有机质含量不同的土壤表现出不同的影响程度;康金林等运用室内模拟土柱试验,得到均质红壤初始含水率越高、入渗率越低,湿润锋运移速率随初始含水率增加而增大;牛文全等采用室内土箱模拟试验方法,研究土壤初始含水率对均质土壤水分扩散的影响,结果表明初始含水率对湿润体形状的影响不大,但对湿润体大小有明显影响。可见,前人的研究中多侧重于不同立地类型、容重条件和初始含水率等的影响。本研究以具有典型代表性的内蒙古准格尔旗砒砂岩区裸露坡面土壤为例,通过室内模拟土柱法探究坡面土壤入渗过程与特征,选择拟合效果最优的入渗模型并进行误差分析,以期为研究区的裸露坡面土壤水分运移和产流汇流提供参考意见。
1 材料与方法
1.1 研究区概况
研究区位于内蒙古自治区鄂尔多斯市准格尔旗暖水乡鲍家沟流域(39°42′—39°50′N,110°25′—110°48′E),地貌类型为丘陵沟壑地貌。该流域自20世纪90年代末实施生态移民政策,隔绝人类开发建设项目的干扰,保留有灌溉条件的耕地,作为水土保持示范田。该地气候类型为中温带半干旱大陆性季风气候,冬季寒冷漫长,夏季炎热短促。雨季主要集中在6—9月,年平均风速3.2 m/s,年平均日照时间2 900~3 100 h,无霜期148天。流域的地带性土壤类型是以砒砂岩为母质发育而来的栗钙土为主,土壤富含石灰,质地以沙土、沙壤土为主。主要树种有柠条()、沙棘()、油松()、侧柏()等。
1.2 研究方法
1.2.1 试验装置 试验装置由有机玻璃土柱和供水系统组成。有机玻璃土柱为圆柱形,高80 cm,半径7.5 cm,用于填装分层土壤。侧面每隔10 cm开有小孔,共8组,小孔处插入金属探头,探头连接HOBO记录仪。有机玻璃圆柱底部设有带孔的塑料挡板和排水口,排水口通过金属阀门控制,试验过程保持排水通畅。供水系统由马氏瓶、软管和支架组成,马氏瓶高40 cm,半径7.5 cm,系统用于提供稳定的入渗水头。有机玻璃圆柱和马氏瓶连接处设有带孔的塑料挡板,并于交界处涂抹凡士林,防止水流的不均匀入渗。
1.2.2 试验材料 试验于2021年7月15日至8月25日进行,土样取自砒砂岩区裸露坡面,且统一取半阴半阳坡的坡中位置0—60 cm土层,并分6层(0—10,10—20,20—30,30—40,40—50,50—60 cm),剔除石砾、植物根系和枯枝落叶等杂质,直接在裸露地表采集,自然风干后过2 mm土筛。混合色土壤采用灰白色土壤和紫红色土壤1∶1配土填装。试验前,用环刀取样,烘干法测定土壤的基本物理性质(表1),并计算每层填装土的重量(公式1)。
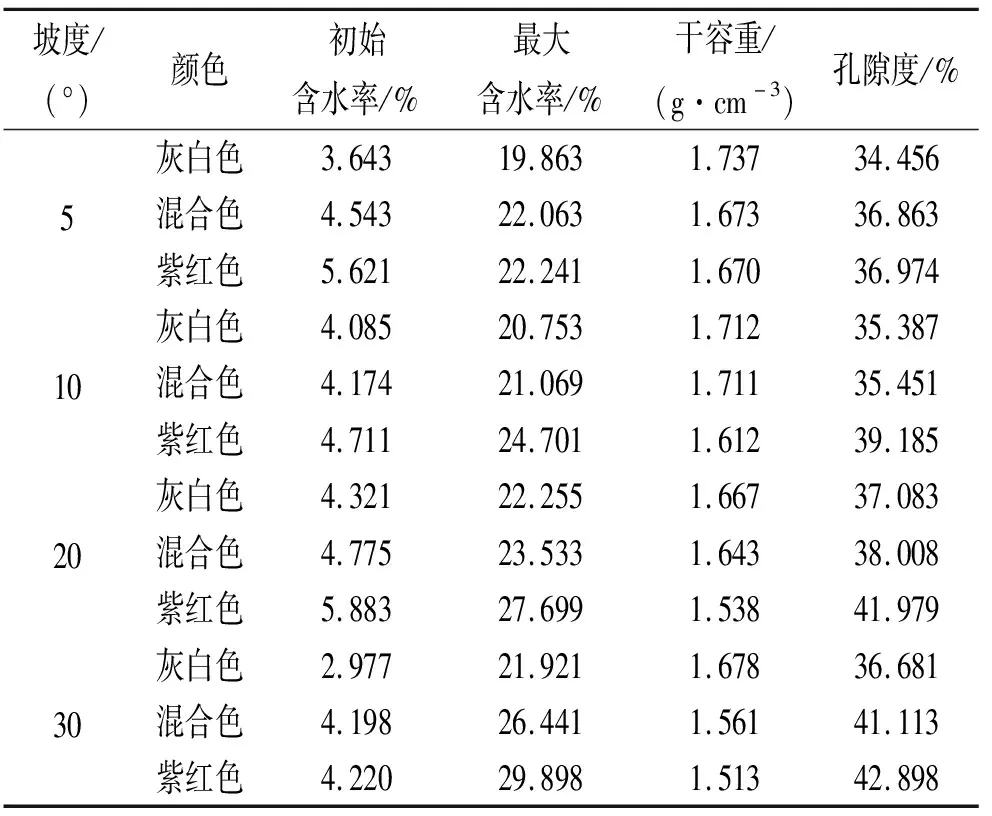
表1 不同坡度下不同颜色砒砂岩土壤基本物理性质
=·(1+)
(1)
式中:为填装土的重量(g);为装入土体体积(cm);为土体干容重(g/cm);为土壤的含水量(%)。
1.2.3 试验设计 本试验对砒砂岩区的土壤采用一维垂直入渗方式,根据流域内典型坡度的分布情况,选取裸露坡面的4种坡度(5°,10°,20°,30°)、3种质地(灰白色、混合色、紫红色)进行组合。每组试验重复3次,共计36组试验。土样按每层5 cm填装,并使用自制陶器压实。在完成每层填装后,用毛刷进行层间打毛,防止土层之间剥离,出现分层现象。完成填充土柱后,在塑料挡板处均匀涂抹凡士林,保证土柱不漏水。打开马氏瓶供水,试验水头为5 cm。达到入渗水头时,开始试验并用秒表计时,马氏瓶刻度和湿润锋深度的读数按照先密后疏的原则并进行记录,时间间隔依次为10 s,30 s,1 min,5 min,30 min,60 min。其中初始入渗速率为前1 min的速率;稳定入渗速率为单位时间内渗透量趋于同一的渗透速率。
1.3 数据分析
采用Excel 2020进行数据统计和图表绘制,Origin 8.5软件进行土壤入渗模型的拟合和参数的回归分析。
1.3.1 模型分析 本试验选取的3种土壤入渗模型为:
(1)Kostiakov模型
()=-
(2)
式中:()为入渗速率(cm/min);为入渗时间(min);和为经验参数。
(2)Philip模型
()=05-05+
(3)
式中:()为入渗速率(cm/min);为入渗时间(min);为吸渗率(cm/min);为稳定入渗率(cm/min)。
(3)Horton模型
()=+(+)e-
(4)
式中:()为入渗速率(cm/min);为入渗时间(min);为初始入渗率(cm/min);为稳定入渗率(cm/min);为反映土壤特征的常数。
1.3.2 误差分析
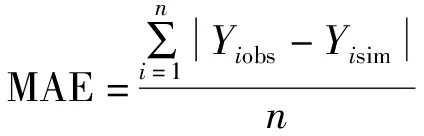
(5)

(6)
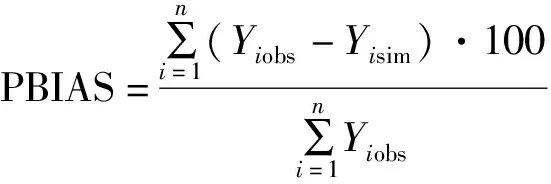
(7)
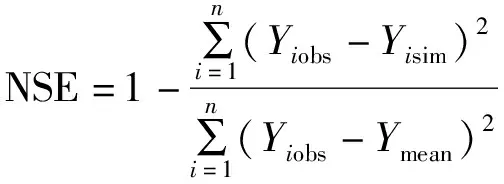
(8)
式中:MAE为平均绝对误差;RMSE为均方根误差;PBIAS为偏差百分比;NSE为纳什效率系数;obs为第个实测值;sim为第个模拟值;为实测值的平均值;为数据总个数。
2 结果与分析
2.1 土壤水分入渗特征
由表2可知,坡度直接影响土壤的湿润锋运移速率。改变坡度条件,水分入渗过程受到影响。坡面越陡,初始入渗速率和初始湿润锋运移速率越高,稳定入渗速率和湿润锋运移速率也相对较高。不同颜色的砒砂岩土壤在一定的坡度条件下,入渗初期湿润锋的运移速率保持在较高水平,随着时间的推移,湿润锋的运移速率逐渐趋于稳定。

表2 不同坡度下土壤水分垂直入渗参数
2.1.1 土壤水分入渗速率的变化 由图1可知,不同坡度条件下土壤入渗速率随时间变化的曲线形态相似,且不同坡度下砒砂岩土壤入渗能力随着入渗时间的增加呈现先下降后逐渐稳定的趋势,入渗速率曲线按照坡度由大到小呈现由上向下分布,均表现为入渗初期的5 min以内入渗速率最快,随着时间延长,入渗速率呈波动性下降趋势。当入渗持续时间约达到20 min以上后,土壤水分环境逐渐饱和,入渗速率下降,最终维持在稳定的入渗速率状态下。
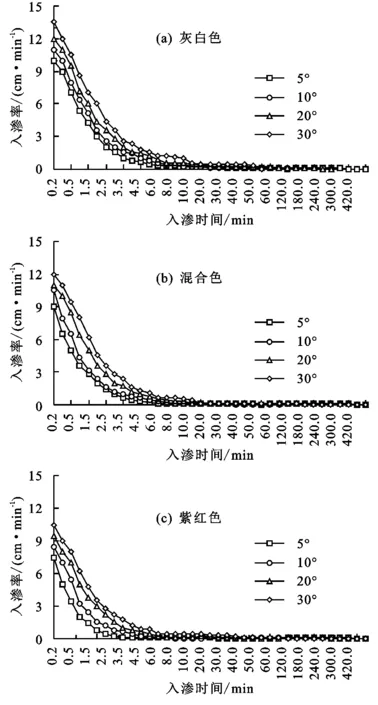
图1 不同坡度下砒砂岩土壤的入渗速率
2.1.2 湿润锋运移的变化 湿润锋是表征水分在土壤基质吸力和重力作用下的运动特征。由图2可知,湿润锋运移速率总体上呈下降趋势,入渗初期湿润锋运移速率保持在较高水平,随着时间的推移,湿润锋运移速率逐渐趋于稳定。不同坡度条件下的湿润锋运移距离均具有显著性差异,坡度越大,湿润锋运移速率越大,湿润锋运移曲线短而陡,湿润锋运移到土柱底部的时间越短;坡度越小,湿润锋运移速率越小,湿润锋运移曲线长而缓,湿润锋运移到土柱底部的时间越长。
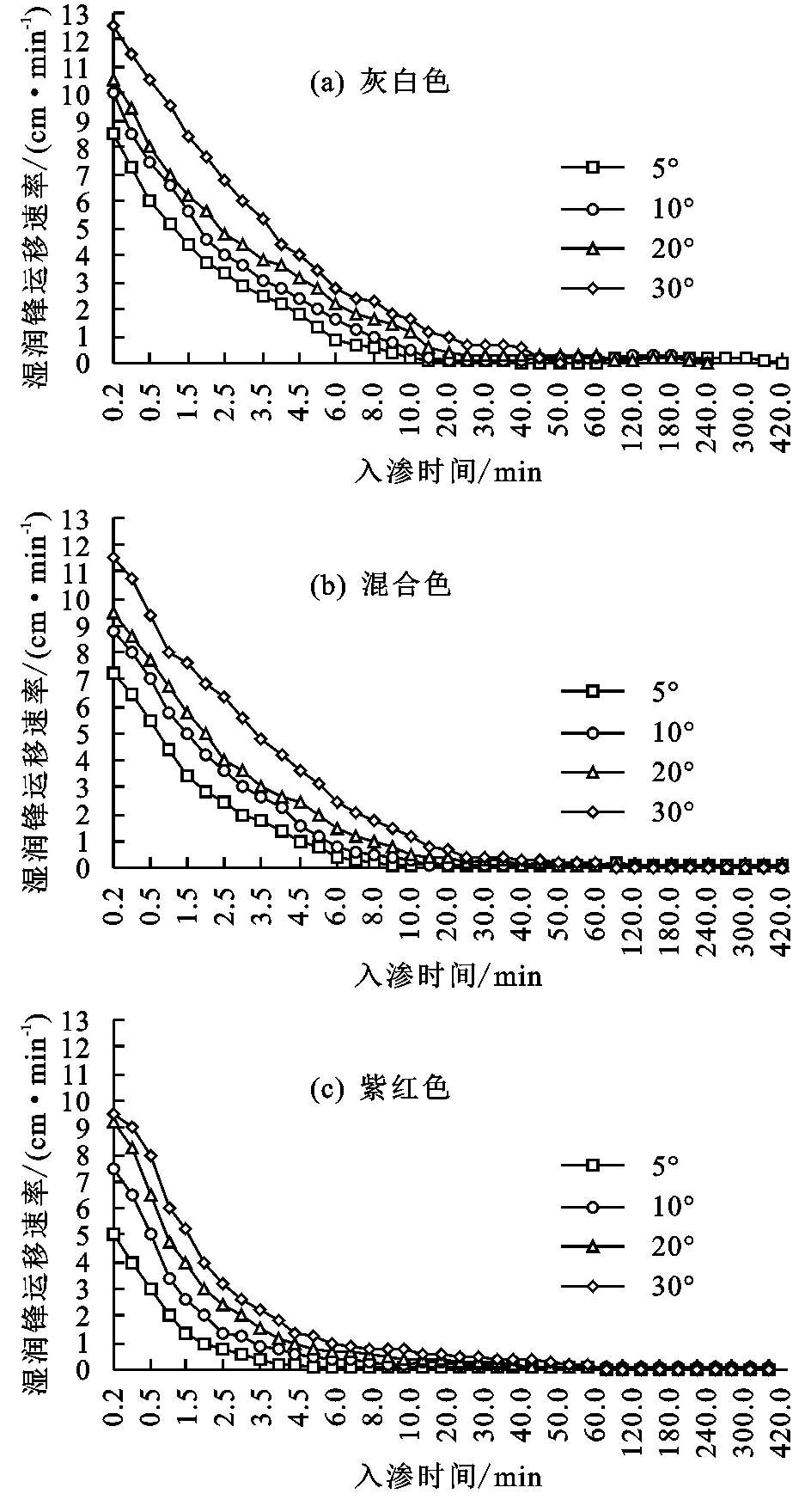
图2 不同坡度下砒砂岩土壤的湿润锋运移速率
2.1.3 累计入渗量的变化 土壤水分的累计入渗量为总入渗水量与入渗土壤表面积的比值。由图3可知,累计入渗量与时间关系曲线表现出幂函数的递减趋势。在入渗初期,相同土柱高度的3种质地砒砂岩土壤累计入渗量曲线斜率变化较大,因此累计入渗量增加的趋势较为显著;变化程度由高到低依次为灰白色、混合色和紫红色。随着时间的推移,入渗速率逐渐减小并趋于稳定,累计入渗量增加的幅度较小。整个入渗过程灰白色的砒砂岩土壤水分累计入渗量最高,而后是混合色和紫红色。

图3 不同坡度下砒砂岩土壤的累计入渗量
2.2 土壤水分入渗模型拟合
由表3可知,Kostiakov模型、Philip模型适用于模拟不同坡度条件下砒砂岩土壤水分的垂直入渗过程。Kostiakov模型的决定系数在0.900以上,平均值为0.948,拟合效果最优;Philip模型的决定系数在0.900以上,平均值为0.937,拟合效果较优;Horton模型的决定系数平均值为0.688,拟合效果较差。

表3 砒砂岩土壤入渗模型回归分析结果
2.3 水分入渗模型拟合检验
通过第1组试验数据的拟合可知,Kostiakov模型和Philip模型的决定系数较高,故利用第2组同期试验数据,并选择平均绝对误差、均方根误差、偏差百分比和纳什效率系数4个指标对这2种模型进行拟合检验(表4)。其中平均绝对误差、均方根误差、偏差百分比的数值越接近0,表明模拟值与实测值的差异越小。纳什效率系数通过无量纲数定量表征过程的拟合程度,反映观测值与模拟值的拟合程度。NSE的取值范围为(-∞,1);当NSE<0,说明模型拟合效果不可信;当0.9 表4 水分入渗模型拟合检验结果 土壤的入渗速率干预地表径流,从而对坡面的水土流失有间接影响。本试验以砒砂岩区裸露坡面不同颜色的土壤为研究对象,该区坡面常伴有基岩的出露,且基岩中的蒙脱石吸水极易膨胀堵塞孔隙,因而不利于水分的入渗过程。本试验表明,砒砂岩区裸露坡面不同颜色的土壤性质存在差异,影响水分入渗。其中,土壤容重是土壤的基本物理性质,间接反映土壤的紧实松散程度、透气和透水能力。土壤容重越小,土壤越松散,土壤总孔隙度和毛管孔隙度越多,土壤入渗能力越强。灰白色砒砂岩土壤疏松,且通气透水性能强;而紫红色砒砂岩土壤相对紧实,通气透水性能差,不利于入渗过程。不同坡度下,灰白色砒砂岩土壤湿润锋达到土柱底部所需最长时间是最短时间的8倍,相差最大;其次是混合色砒砂岩土壤,紫红色砒砂岩土壤相差最小,且这2种土壤湿润锋运移的时间都达到8 h以上,与前人的研究结果相符。 通过对入渗速率与入渗时间建立数学关系进行模拟,可在一定程度上反映水分在土壤中的入渗过程,决定系数反映自变量引起的变动占总变动的百分比。本试验通过3种数学模型对入渗过程进行拟合,结果表明,Kostiakov模型和Philip模型拟合效果较好。Kostiakov模型效果最优,Horton模型效果较差,且误差主要集中在5°坡面条件下。Kostiakov模型对灰白色土壤的模拟误差较大,Philip模型对紫红色土壤的模拟误差较大。同时,Kostiakov模型虽然无法直接反映土壤的理化性质,但具有参数获取简单的突出优点。在入渗初期经验入渗参数起主导作用,随着入渗时间的增长,参数成为影响入渗大小的主要因素。本试验表明,该模型在确定观测时间的前提下,参数能较为准确地反映初始入渗速率与入渗速率的衰减幅度。通过对不同模型的误差分析证明Kostiakov模型对于砒砂岩区裸露坡面水分入渗过程的研究具有较强的适用性。 (1)研究区不同坡面土壤容重为1.513~1.737 g/cm,初始含水率为3.643%~4.220%,孔隙度为34.456%~42.898%,30°坡面下的灰白色砒砂岩土壤入渗能力较强,5°坡面下的紫红色砒砂岩土壤入渗能力较弱。 (2)坡度的大小、砒砂岩的质地均影响砒砂岩土壤入渗能力,坡度越小,颜色越深,入渗率、累计入渗率越低,湿润锋运移越慢;且初始入渗速率、稳定入渗速率、初始湿润锋运移速率、稳定湿润锋运移速率均呈现减小趋势。 (3)Kostiakov模型、Philip模型均适用于模拟不同坡度条件下砒砂岩土壤水分的垂直入渗过程,回归系数较优;且Kostiakov模型最优,对砒砂岩区土壤入渗的适用性更强。通过平均绝对误差、均方根误差、偏差百分比、纳什效率系数验证Kostiakov模型和Philip模型模拟值与实测值差异性小,两者的吻合程度高。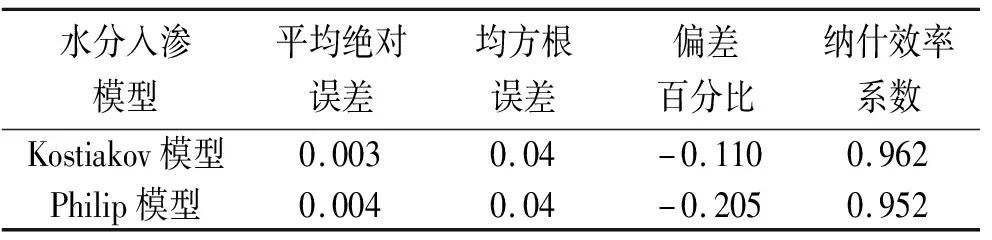
3 讨 论
4 结 论

